585

4. Виды уравнений плоскости в пространстве:

–общее уравнение и его важные частные случаи;

–уравнение «в отрезках»;

–уравнение плоскости, проходящей через одну или три заданные точки.

5. Геометрический смысл коэффициентов, входящих в уравнения плоскости.

6. Алгоритмы решения основных задач для плоскости:

–построение плоскости в прямоугольной системе координат по ее уравнению;

–нахождение уравнения плоскости по условиям задачи;

–переход от одного вида уравнения к другому виду;

–вычисление угла между пересекающимися плоскостями, определение перпендикулярности и параллельности плоскостей;

–определение расстояния от заданной точки до плоскости.

7. Виды уравнений прямой в пространстве:

–общие уравнения прямой как линии пересечения двух плоскостей;

–уравнения прямой, проходящей через две заданные точки;

–канонические и параметрические уравнения прямой.

8.Геометрический смысл коэффициентов, входящих в уравнения прямой.

9.Алгоритмы решения основных задач для прямой в пространстве:

– построение прямой по координатам двух заданных точек;

– приведение общих уравнений прямой к каноническим или параметрическим уравнениям;

– вычисление угла между пересекающимися прямыми, определение перпендикулярности и параллельности прямых;

– определение расстояния от заданной точки до прямой;

– определение взаимного положения двух прямых в пространстве.

10.Алгоритмы для решения прямой и плоскости в простран-

стве:

– вычисление угла между прямой и плоскостью;

– определение взаимного положения прямой и плоскости (перпендикулярность, параллельность, расположение прямой в плоскости);

173

Указанный способ удобен тем, что позволяет использовать единообразное описание кривых в n-мерных пространствах. В частности, в трехмерном пространстве параметрические уравнения кривой имеют вид

x = x(t)y = y(t).

z = z(t)

В прямоугольной системе координат пространственную кривую можно определить как линию пересечения двух поверхностей

f (x, y, z) = 0g (x, y, z) = 0 .

Замечание: В частном случае прямая в пространстве в прямоугольных координатах определяется как линия пересечения двух плоскостей.

Если левая часть уравнения f (x, y) = 0 является многочле-

ном степени n, то такая линия называется алгебраической линией n -го порядка.

Наибольшее прикладное значение имеют алгебраические кривые второго порядка, которые описываются уравнением вида

A12 + A22 + A32 ≠ 0.

Если A1 = A2 = A3 = 0, то получим уравнение первого порядка, которому соответствуют линейные геометрические объекты (плоскости и прямые). Алгебраические кривые второго порядка являются нелинейными геометрическими объектами.

Уравнение кривой второго порядка можно существенно упростить за счет линейных смещений и поворотов прямоугольной системы координат. Наиболее простой вид алгебраические кривые второго порядка имеют в специальных (канонических) прямоугольных системах координат. При этом порядок алгебраических кривых при преобразованиях координат не изменяется (многочлен в левой части уравнения остается многочленом второго порядка).

175

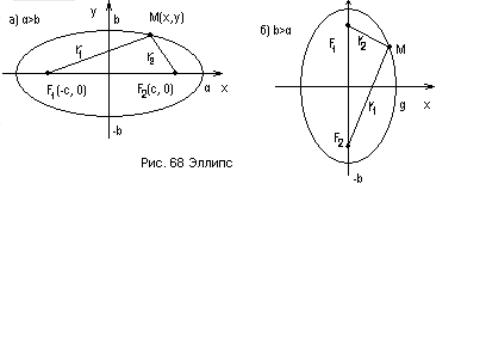
4.5.20. Эллипс

Определе ние: Эллипсом называется алгебраическая кривая второго порядка, каждая точка которой удалена от двух фиксированных точек (фокусов), не принадлежащих эллипсу, так, что сумма расстояний от фокусов до любой точки эллипса постоянна.

Обозначим фокусы буквами F1, F2, расстояние между фокусами обозначим 2с. Это расстояние называется фокальным (фокусным). Поместим начало прямоугольной системы координат xOyв середину отрезка F1F2 так, чтобы направление вектора F1F2 совпало с положительным направлением координатной оси, которая называется фокальной осью.

Расстояние с от начала координат до фокуса называется линейным эксцентриситетом эллипса. Расстояния от начала координат до наиболее и наименее удаленных точек (вершин) эллипса (a и b) называются полуосями эллипса. При этом отрезок наибольшей полуоси лежит на фокальной оси эллипса. Расстояния от фокусов эллипса до любой его точки называются фокальными радиусами. Если фокальная ось эллипса совпадает с координатной осью Ox (рис. 68, а), то a > b и характеристическое свойство эллипса, лежащее в основе его определения, в математической форме имеет вид r1 + r2 = 2a, линейный эксцентриситет

если фокальной осью эллипса является координатная ось Oy (рис. 68, б) то при a < b имеют место равенства r1 + r2 = 2b и c = 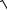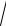b2 − a2 .

177

Пример 1. Задано уравнение эллипса x2 + y2 =1. Найти 25 64

параметры эллипса (длины полуосей, линейный и относительный эксцентриситеты); построить эллипс по характерным точкам (точки пересечения эллипса с осями координат, фокусы); проверить правильность построения по его характеристическому свойству.

Решение: полуоси эллипса равны a = 25 = 5, b = 64 = 8. Поскольку a < b, то фокусы эллипса лежат на оси Oy. Расстояние от начала координат до фокусов (линейный эксцентриситет):

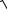
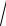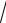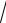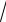c = b2 − a2 = 64 − 25 = 39 ≈ 6,25. Координаты фокусов: F1 (0, 39), F2 (0, − 39).

Определим абсциссы точек M1, M2 , принадлежащих эллипсу, при одинаковых ординатах y = 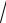39 :

построения эллипса

M2 (−3,125; 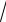39). Строим эллипс (рис. 70).

Производим проверку, используя характеристическое свойство эллипса r1 + r2 = 2b:

r1 = F1M1 = 3,125;

r2 = F2M1 = (3,125 − 0)2 + (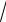39 − (−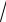39))2 = 12,875;

r1 + r2 = 3,125 +12,825 = 2b = 2 8 =16.

Пример 2. Составить каноническое уравнение эллипса, если известны его эксцентриситет – 0,8 и уравнение директрисы x =12,5.

Решение: Поскольку директриса вертикальна, то a > b и, зна-

чит, e = c , Составим систему уравнений для нахождения полу- a

осей эллипса:

179

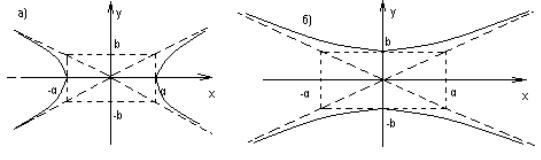
Расстояние с от начала координат до фокуса называется линейным эксцентриситетом гиперболы. Расстояние от начала координат до любой из точек пересечения (вершин) гиперболы с ее действительной осью называется действительной полуосью.

Расстояния от фокусов гиперболы до любой его точки называются фокальными радиусами. Если действительная ось гиперболы совпадает с координатной осью Ox (рис. 71, а), то характеристическое свойство гиперболы, лежащее в основе его определения, в математической форме имеет вид r1 − r2 = 2a, линейный

x2 y2

эксцентриситет c = a2 + b2 , каноническое уравнение a2 − b2 =1,

где b – мнимая полуось гиперболы. Аналогично, если действительной осью гиперболы является координатная ось Oy (рис.71, б) то действительная полуось гиперболы равна b, фокусы лежат на оси Oy, характеристическое свойство имеет вид r1 − r2 = 2b,

линейный эксцентриситет c = 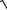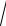a2 + b2 , а каноническое уравнение

y2 x2

гиперболы имеет вид b2 − a2 =1.

Оси координат Ox, Oy являются осями симметрии гиперболы, а начало координат – центром симметрии. Гипербола состоит их двух ветвей, симметричных относительно мнимой оси; каждая ветвь пересекает действительную ось. При неограниченном увеличении координат x и y точек гиперболы ветви гиперболы неограниченно приближаются к наклонным прямым, которые называются

асимптотами гиперболы и имеют уравнения y = b x и y = − b x. a a

Если a = b, то асимптоты будут взаимно ортогональными ( y = x, y = −x). Если эти асимптоты использовать в качестве координатных осей, то уравнение гиперболы будет иметь вид

y = m , m = const. Это уравнение называется уравнением обрат- x

ной пропорциональности (рис. 72).

Замечание: асимптоты гиперболы обладают следующим свойством: расстояние от точки асимптоты до гиперболы неограниченно уменьшается при удалении от начала координат.

181

Рис. 72. График обратной пропорциональности

Для оценки влияния изменения длин полуосей гиперболы на форму ее ветвей обычно используют относительный эксцентриситет (1< e < ∞):

e = c , если a – действи- a

тельная ось гиперболы;

e = c , если b – действитель- b

ная ось гиперболы.

При e →1 ветви гиперболы «выпрямляются», приближаясь к параллельным прямым, перпендикулярным действительной оси; при e → ∞ ветви гипербо-

лы «складываются», приближаясь к действительной оси.

Для определения гиперболы можно использовать ее директориальное свойство (рис. 73).

Определе ние: Две прямые, перпендикулярные фокальной

стояние b ), называются директрисами гиперболы. e

182