
569
.pdf
Можно ввести универсальное определение медианы. Медиана xmed — это такое значение случайной величины Х,
1
что F(xmed) = P(X < xmed) = P(X > xmed) = 2 . То есть вероятность того, что случайная величина X примет значение мень-
1
ше, чем xmed, равна 2 (рис. 9).
Рис. 9. Универсальное определение медианы
6. Асимметрия (асимметричность) — характеристика симметричности функции плотности распределения (многоугольное распределение) относительно моды. Для дискретной случайной величины асимметрия вычисляется по формуле
n |
|
|
As (xi |
)3pi / 3, а для непрерывной — |
|
i |
|
|
|
|
|
As |
(x )3f(x)dx/ 3 (рис. 10). Асимметрия нормаль- |
|
но распределенной случайной величины считается равной нулю. У нормально распределенной случайной величины (НРСВ) функция плотности распределения описывается формулой
|
|
1 |
|
|
(x )2 |
|
|
f(x) |
|
|
e 2 2 . |
||||
|
|
|
|||||
2 |
|||||||
|
|
|
|
|
|||
X
Рис. 10. Виды функций плотности распределений с различными значениями асимметрии
21
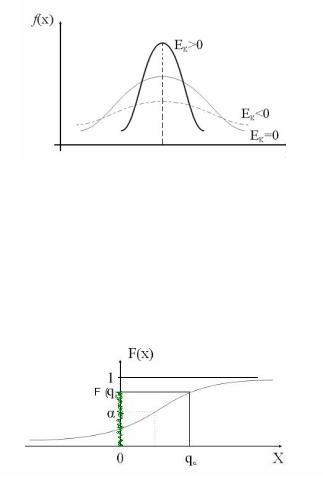
7. Эксцесс — характеристика островершинности кривой функции плотности распределения по сравнению с нормально распределенной случайной величиной с такими же значениями математического ожидания М(X) и дисперсии D(X) (рис. 11). Для дискретной случайной величины эксцесс вычисляется по
n
формуле Ek (xi )4 pi / 4 3, а для непрерывной —
i 1
Ek (x )4f(x)dx/ 4 3.
X
Рис. 11. Виды функций плотности распределений с различными значениями эксцесса
Примечание. По значению эксцесса можно судить о разбросе данных относительно математического ожидания. Если эксцесс положительный, то разброс данных меньше, чем у НРСВ; если отрицательный, то больше, чем у НРСВ (см. свойства функции плотности распределения).
8. Квантиль q — это такое значение случайной величины Х, при котором функция распределения принимает значение, равное . F(q) = (рис. 12).
Рис. 12. Геометрическая интерпретация квантиля
22

Вводят специальные значения квантиля: q0,25 — нижний квартиль (от слова кварта — четверть); q0,75 — верхний квартиль; q0,5 — медиана.
2.3. Некоторые специальные законы распределения
2.3.1.Биномиальноераспределение
Рассмотрим частный случай распределения дискретной случайной величины. Пусть производится n независимых испытаний. В каждом из них может произойти с вероятностью p событие A и не произойти с вероятностью q = 1 – p.
Пусть X дискретная случайная величина, равная числу появления события A. Величина X может иметь такие значе-
ния: x = 0; x = 1; …; x = n.
Формула Бернулли позволяет найти вероятность появления события A в n испытаниях ровно k раз по формуле Pk(k)=
= C mpk(1 – p)n–k, где Cm |
|
n! |
. |
|
|
||||
n |
n |
|
k!(n k)! |
|
|
|
|
||
Закон распределения, определяемый формулой Бернулли, называется биномиальным.
Приближенное значение Pn(k) при больших n и малых p
можно аппроксимировать формулой Пуассона Pn(k) ke , k!
где = n p.
Для закона Бернулли математическое ожидание и дисперсия случайной величины X = k можно вычислить по формулам M(X) = np и D(X) = npq соответственно.
Рассмотрим двухточечное распределение для одного испытания случайной величины. Пусть x = 0, если событие A не наступило; x = 1, если наступило. Вероятности данных событий равны соответственно P(x = 0) = 1 – p и P(x = 1) = p. Математическое ожидание в этом случае равно M(X) = = 0(1 – p) + 1p = p, а дисперсия вычисляется по формуле
D(X) = p – p2 = p.
23

2.3.2. Геометрическое распределение
Схема здесь такая же, что и у биномиального распределения. Испытания заканчиваются, когда событие A произойдет.
Пусть x — число испытаний до первого появления события A. Тогда вероятность, что число испытаний равняется k, можно
вычислить по формулеP(x = k) = qk – 1p; x < . Математичес-
кое ожидание и дисперсия равны соответственно M(X) 1 ; p
1 p D(X) p2 .
2.3.3. Распределение Пуассона
Здесь схема испытаний, как и у биномиального закона. Только пусть при числе испытаний n имеем = np = const, т.е. имеет место массовые испытания редких событий.
Вероятность того, что событие A в n испытаниях появится
ровно k раз, вычисляется по формуле Pn(k) ke . Эта ве- k!
роятность зависит только от .
Математическое ожидание и дисперсия равны соответственно
M(X) = ; D(X) = .
2.3.4. Равномерное распределение
Равномерное (прямоугольное) распределение можно задать
функцией плотности распределения f(x) |
1 |
при a < x < b |
|||
b a |
|||||
|
|
|
|
||
(рис. 13) или функцией распределения |
F(x) |
x a |
(рис. |
||
b a |
|||||
|
|
|
|
||
14). У равномерно распределенной случайной величины
|
a b |
|
(b a)2 |
|||
M(X) |
|
xmed; |
D(X) |
|
. |
|
2 |
||||||
|
||||||
|
|
|
b a |
|||
24
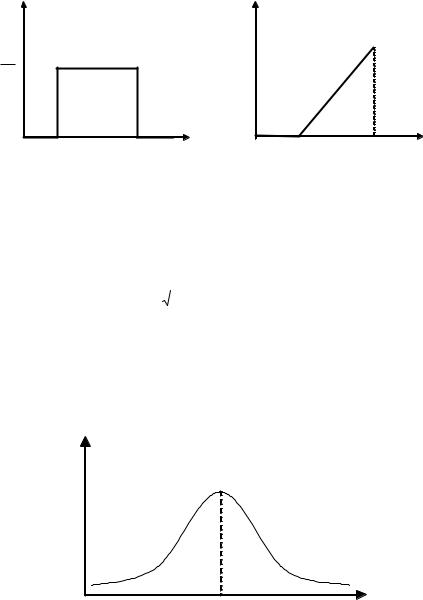
f(X) |
F(X) |
1 
1
b a
a |
b |
X |
a |
b |
X |
Рис. 13. Функция плотности |
Рис. 14. Функция |
|
|||
равномерного распределения |
равномерного распределения |
||||
2.3.5. Нормальноераспределение
Функция плотности нормального распределения описыва-
|
|
1 |
|
|
(x )2 |
|
|
ется формулой f(x) |
|
|
e 2 2 (рис. 15). Случайная ве- |
||||
|
|
|
|||||
2 |
|||||||
|
|
|
|
|
|||
личина X изменяется – < x < + . У данного распределения два параметра: — математическое ожидание; 2 — дисперсия. Функция распределения выражается формулой
x
F(x) f(u)du (рис. 16).
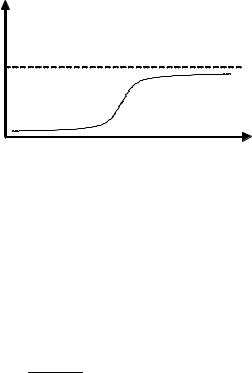
f(X
|
X |
Рис. 15. Функция плотности нормального распределения
25
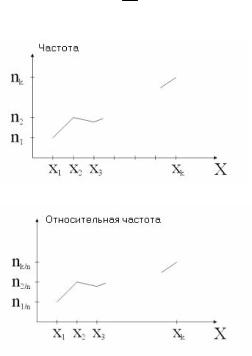
F(X)
1
X
Рис. 16. Функция нормального распределения
У нормально распределенной случайной величины M(X) == xmed = xmod; D(X) = 2. Справедливы следующие правила:
P( x ) 0,68; |
P( 2 x 2 ) 0,95; |
P( 3 x 3 ) 0,97 (правило «трех сигм»). Двухмерный закон распределения нормальной случайной
величины (X, Y) можно описать функцией распределения F(x,y) P((X,x) (Y y)) или функцией плотности распре-
деления f(x,y) F(x,y).
x y
Причем выполняются следующие соотношения: M(X,Y) =
D(x) (MX),M(Y)); D(X,Y)
cov(X,Y) риация cov(X,Y) cov(Y,X) xy;
xy M[(X M(X))(Y M(Y))]
cov(X,Y)
, здесь кова-
D(Y)
|
|
|
|
|
|
|
|
|
|
[(x M(X))(y M(Y))f(x,y)]dxdy. |
|||||
|
|
|
|
|
|
|
|
Коэффициент корреляции между X и Y может быть опре- |
|||||||
делен по формуле |
|
|
xy |
|
|
||
1 xy |
x |
|
|
1. |
|||
|
|
||||||
|
|
|
|
|
y |
||
26
Контрольные вопросы к разделу 2
1.Понятие случайного события. Дискретные и непрерывные случайные величины.
2.Свойства и геометрический смысл функции распределения и функции плотности распределения.
3.Как вычислить вероятность попадания случайной вели-
чины в интервал (a, b]?
4.Основные числовые характеристики.
5.Специальные законы распределения.
3.ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ СЛУЧАЙНЫХ ВЕЛИЧИН. СТАТИСТИЧЕСКАЯПРОВЕРКАГИПОТЕЗ
Знания законов распределения случайных величин достаточно для проведения полных вероятностных расчетов.
Однако при решении прикладных задач обычно ни законы распределения, ни значение их числовых характеристик не известны. Поэтому исследователь обращается к обработке опытных данных, которые получены в результате проведенного эксперимента.
Основные задачи в этом случае следующие:
—указать способы сбора и группировки опытных (эмпирических) данных;
—разработать методы анализа статистических данных в зависимости от целей исследования.
Введем понятия генеральной совокупности и выборки. Под генеральной совокупностью будем понимать совокуп-
ность всех мыслимых наблюдений, которые могли бы быть сделаны при данном комплексе условий.
Но на практике исследование всей генеральной совокупности либо слишком трудоемко, либо принципиально невозможно. Например, определить продолжительность работы лампочки. Если мы будем проводить исследование всей генеральной совокупности, то нечем будет освещать комнаты. Приходится ограничиваться анализом лишь некоторой выборки из анализируемой генеральной совокупности.
Наблюдения выборки получены с помощью случайного механизма из генеральной совокупности, причем каждое из наблюдений имеет одинаковый шанс попасть в выборку.
27
Назначение статистических методов состоит в том, чтобы на основе анализа выборки V выносить обоснованное суждение о всей генеральной совокупности.
Пусть из генеральной совокупности извлечена выборка V. х1 наблюдается n1 раз.
х2 наблюдается n2 раз.
……………………….
хk наблюдается nk раз.
k
ni n — объем выборки (число элементов в выборке).
i 1
Наблюдаемые значения xi называют вариантами, последовательность вариант в возрастающем порядке — вариационным рядом.
3.1. Частота
Числа наблюдений ni называются частотами (рис. 17), а их
отношение к объему выборки ni wi — относительными час- n
тотами (рис. 18).
Рис. 17. Полигон частот
Рис. 18. Полигон относительных частот
28
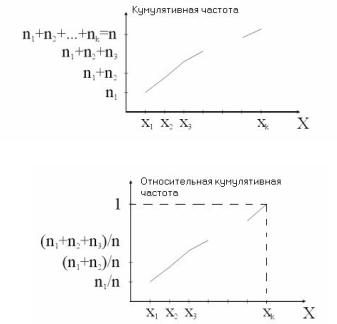
Введем еще понятия кумулятивной (интегральной) частоты (рис. 19) и относительной кумулятивной частоты. Формула
j
вычисления кумулятивной частоты Ej ni (число наблю-
i 1
дений вариант x1,x2, …, xj в вариационном ряду, причем Ek = n),
j
а относительной кумулятивной частоты — Ejотн ni /n
i 1
(рис. 20).
Рис. 19. Полигон кумулятивных частот
Рис. 20. Полигон относительных кумулятивных частот
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот (табл. 3).
Таблица 3
Статистическое распределение выборки
xi |
2 |
6 |
12 |
ni |
3 |
10 |
7 |
29
Эмпирической функцией распределения называют функцию F*(x), определяющую для каждого значения х относительную
j
кумулятивную частоту события Х < x: F*(x) ni /n, где
i 1
nx — частоты попадания в интервалы, лежащие левее x; n — объем выборки.
F(x) — функция распределения для генеральной совокупности. Ее называют теоретической функцией распределения.
Пример нахождения эмпирической функции распределения. Исходные выборочные данные приведены в табл. 4.
Таблица 4
Исходные данные
xi |
2 |
6 |
12 |
ni |
3 |
10 |
7 |
k
Вычислим объем выборки n ni 3 10 7 20.
i 1
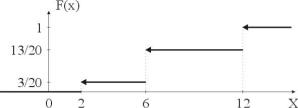
Эмпирическая функция распределения получится следующего вида:
|
0, |
x 2 |
|
|
|
2 |
x 6 |
* |
3/20, |
||
F |
(x) |
|
x 12 |
|
13/20, |
6 |
|
|
|
x 12 |
|
|
1, |
||
Графически данная функция представлена на рис. 21.
Рис. 21. Эмпирическая функция распределения
Примечание. Отличие теоретической функции распределения F(x) от эмпирической функции распределения F*(x) состоит в том, что F(x) определяет вероятность события Х < х, а F*(x) определяет относительную кумулятивную частоту этого события X < x.
30
