Chislennoe_differentsirovanie_funktsiy

Численное дифференцирование функций

В предыдущих лекциях были рассмотрены способы приближенного аналитического представления функций, заданных своими значениями в нескольких точках. Это также решает задачу приближенного дифференцирования, поскольку дифференцирование интерполяционного многочлена не представляет никаких трудностей. Однако мы рассмотрим другой способ получения формул численного дифференцирования, который приводит к тому же результату, но является более простым.

Пусть функция f(x) дифференцируема в точке x. Тогда значение производной определяется следующим образом

(1)

Для вычисления производной необходимо проведение ряда операций. Некоторые из них практически осуществимы: мы можем вычислять значения функции и проводить с ними арифметические действия. Но мы не можем вычислять пределы, поскольку это требует бесконечных затрат ресурсов (времени, памяти и т.д.). В связи с этим ограничимся конечными . Получим приближенные формулы

. (2)

Пусть задана сетка - шаг сетки. Введем обозначение , и т.д. Тогда (2) можно переписать в виде

. (3)

Первое из этих трех отношений носит название правой разностной производной, второе – левой, третье – центральной разностной производной.

Для приближенного вычисления второй производной используем формулу центральной разностной производной

. (4)

Отметим, что значения правой и левой разностных производных в точке одновременно являются центральными разностными производными и , рассчитанными соответственно в точках и (рис. 3.1).

Рис 3.1. К задаче численного дифференцирования

Тогда

. (5)

Теперь необходимо оценить погрешность метода, связанную с заменой предельных значений на конечно-разностные.

Рассмотрим правую разностную производную. Для оценки разложим f(x) по формуле Тейлора.

. (6)

Положим в (6)

. (7)

Отсюда

. (8)

Выражение слева представляет собой правую разностную производную, справа – сумму точного значения производной и остаточного члена, который представляет собой погрешность. Ее можно оценить, если известна верхняя оценка второй производной

. (9)

Для левой разностной производной оценка получается аналогично. Рассмотрим центральную разностную производную. Разложение f(x)

. (10)

При и

, (11)

. (12)

Вычитая (12) из (11) и выражая , получим оценку

. (13)

Погрешность второй разностной производной оценим аналогичным способом. Разложим f(x)

.

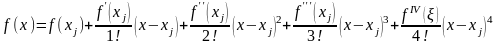При и

, (14)

. (15)

Складывая (14) и (15) получим

. (16)

Разделив (16) на h₂ и перенеся влево 2f_j, получим оценку

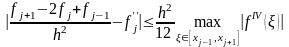. (17)

Таким образом, получены оценки погрешности разностных производных (3) и (5).

Показатель степени при h в формулах для оценки погрешности называется порядком точности формулы. Таким образом, правая и левая разностные производные имеют первый порядок точности, центральные разностные производные (первая и вторая) – второй порядок.

Отметим, что для оценки погрешности первой разностной производной необходимо знать оценку второй или третьей производной, для оценки погрешности второй разностной производной – оценку четвертой производной. Это не позволяет использовать формулы (9), (13), (17) непосредственно для практической оценки погрешности. По существу, такие оценки пригодны лишь для теоретических исследований. Полезной для практических целей информацией можно считать, по-видимому, только порядок точности формулы. Как получить оценку погрешности практически, будет сказано далее.

Оценим погрешность, возникающую в связи с усечением чисел (погрешность исходных данных).

Поскольку при вычислении значений функции мы вынуждены ограничиваться конечным числом разрядов мантиссы M, в конечно-разностных формулах вместо точных значений функции f_j мы вынуждены использовать приближенные f_j+_j. Например, для правой разностной производной

Общая погрешность

. (18)

Первое слагаемое (18) оценивается, согласно (9), функцией ch, где . Каждую из погрешностей _j можно оценить по модулю сверху предельной погрешностью , которую нетрудно найти, зная относительную погрешность чисел в машинном представлении (лекция 1) и оценку функции :

.

Тогда общую погрешность (18) можно оценить величиной

. (19)

График зависимости приведен на рис. 3.2.

Рис 3.1. Минимизация общей оценки погрешности

Найдем минимум функции (19). Для этого продифференцируем

.

Отсюда найдем

. (20)

Подставим в (19).

. (21)

Из (20) следует, что порядок величины h должен быть согласован с длиной мантиссы машинного слова, а именно, шаг не должен быть меньше, чем . Такой же порядок имеет минимальная оценка погрешности (21). Тем самым, при применении рассмотренной формулы численного дифференцирования (первого порядка точности) теряется, как минимум, половина разрядов.