
3357
.pdf
Зубчатые механизмы с неподвижными осями по типу исполнения разделяют на передачи с последовательным соединением зубчатых колес (рядовые) и ступенчатые.
Рядовая передача
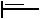

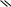
 z 1
z 1
z 2
z 3
V1 |
1 |
|
Vn
2 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
Рис. 3.7
Ступенчатая передача
|
3 |
4 |
|
|
5 |
6 |
|
1 |
2 |
||
|
|||
|
8 |
n-1 |
|
|
7 |
n |
|
|
9 |
n-2 |
|
|
Рис. 3.8 |
|
69
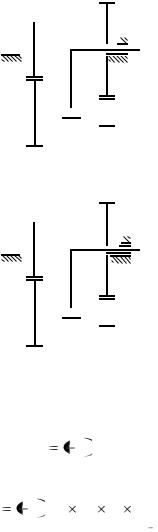
Зубчатые механизмы с подвижными осями:
Планетарные
 z4
z4 


 z1
z1 

z2 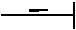 z3
z3
Рис. 3.9
Дифференциальные
 z4
z4 

 z1
z1 

z2 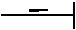 z3
z3
Рис. 3.10
Передаточное отношение для последовательного ряда зубчатых колес и ступенчатых передач:
|
|
U1n |
1 |
k |
zn |
|
|
|||
|
|
|
|
z1 |
|
|||||
|
|
|
|
|
|
|
|
|
||
U |
|
1 k |
z2 |
|
z4 |
|
|
zn |
||
1n |
z1 |
|
z3 |
zn 1 |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||
|
u |
=(–1) z /z z /z |
|
z /z, |
||||||
где k – число пар колес внешнего зацепления.
70

В планетарных и дифференциальных механизмах движение может передаваться от центральных колес z , z к водилу H и от водила H к колесам.
Для вычисления передаточных отношений таких механизмов используют метод инверсии (обращенного движения). При этом рассматривают движение всех колес относительно водила, тогда угловая скорость водила будет равна нулю, угловые скорости колес станут меньше действительных (абсолютных) на величину угловой скорости водила.
 z4
z4 


 z1
z1 
z2  z3
z3
Рис. 3.11
Полученный таким образом механизм (обращенный механизм) представляет ступенчатую передачу, передаточное отношение которой:
U H |
1 |
H |
14 |
|
|
4 |
H |
|
Из последней формулы можно определить передаточное отношение для планетарного механизма (ω4 =0):
U H |
1 H |
1 U 4 |
|
||
14 |
|
1H |
H
Передаточное отношение планетарного механизма при ведущем водиле:
71

U 4 |
1 |
|
|
|
|
|
|
|
H 1 |
U 4 |
|
|
||
|
|
1H |
где U1H4 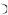 передаточное отношение при ведущем центральном колесе 1.
передаточное отношение при ведущем центральном колесе 1.
4. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
МКЭ первоначально появился в строительной механике, сейчас он широко применяется во многих научных и инженерных приложениях.
МКЭ характеризуется следующими свойствами:
1)физическая область делится на подобласти или конечные элементы;
2)зависимая переменная (одна или несколько) аппраксимируется функцией специального вида на каждом конечном элементе и, следовательно, во всей области. Параметры этих аппроксимаций в последующем становятся неизвестными параметрами задачи;
3)подстановка аппроксимаций в определяющие уравнения дает систему множества уравнений с неизвестными параметрами. Решая эти уравнения, можно определить значения этих параметров и, следовательно, получить приближенное решение задачи. Так как число неизвестных в окончательной системе уравнений часто весьма велико, то общепринято использовать матричные обозначения, как для сокращения записи, так и для облегчения программирования.
Метод конечных элементов предполагает процедуру решения для непрерывной системы, т.е. системы, охватывающей явление в непрерывной области.
4.1. Строительные конструкции
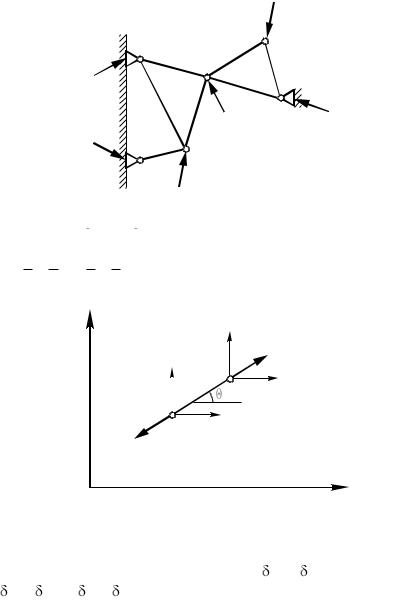
Рассмотрим плоскую шарнирно-соединенную ферму. Предполагается, что ферма собрана без предварительного напряжения, а нагрузки приложены в узлах (рис.4.1).
72
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
R3 |
|
|
_ |
|
|
|
|
3 |
|
|
|
|
6 |
e1 |
|
e6 |
|
|
|
|
R6 |
|
2 |
e |
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
7 |
_ |
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
e4 |
_ e5 |
1 |
R1 |
|
|
|
|
|
R2 |
|
|
|
|
_ |
|
e3 |
|
4 |
|
|
|
|
R5 |
|
|
|
|
|
|
|
|
|
5 |
|
_ |
|
|
|
|
|
|
|
|
R4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.1 |
|
|
|
Силы |
F2 |
и |
F3, действующие в шарнирах на типовой |
|||||
элемент е6 |
представлены на |
рис.4.2 |
в |
виде их проек- |
||||
ций Fx2 , Fy2 и Fx3 |
,Fy3 |
на оси х, у, соответственно. |
||||||
y |
|
|
_ |
|
|
|
_ |
Fy |
_ |
|
|
3 |
P |
|
|
|
|
||
|
|
Fy |
|
|
|
|
3 |
_ |
|
|
|
2 |
||
|
|
|
|
|
|
|
|
e6 |
Fx3 |
|
|
2 |
_ |
|
|
|
|
||
|
_ |
|
|
|
|
|
Fx |
|
|
|
P |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
x |
|
|
|
Рис. 4.2 |
|
Смещения узлов элемента от них исходного положения (до приложения нагрузки) обозначим  2 и
2 и  3 с компонентами
3 с компонентами
 x2,
x2,  y2 и
y2 и  x3,
x3,  y3 соответственно. В матричной форме:
y3 соответственно. В матричной форме:
73
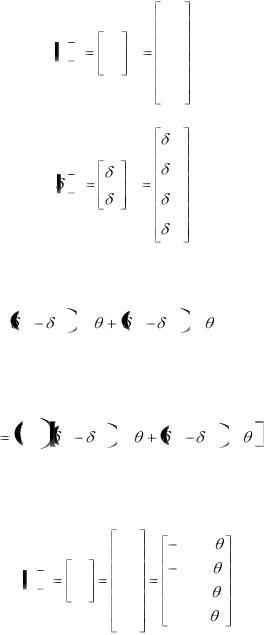
|
|
|
|
|
|
Fx2 |
e6 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
F |
e6 |
Fy |
|
|
|
|
|
e |
|
|
2 |
|
|
|||
F |
6 |
2 |
|
|
|
(4.1) |
|||
|
F3 |
|
Fx |
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
Fy3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
e6 |
|
|
|
|
|
e |
|
|
|
y2 |
|
|
||
|
6 |
2 |
, |
(4.2) |
|||||
|
|
||||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
x3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
y3
где индекс е6 обозначает элемент, к которому относятся рассматриваемые величины.
Растяжение или сжатие стержня длины L определяется
|
|
|
|
|
|
|
|
|
|
|
|
|
величиной х |
3 |
|
х |
2 |
cos |
y |
3 |
|
y |
2 |
sin и деформация полу- |
|
|
|
|
|
|
|
|
|
|
||||
чается в результате деления этой величины на L.
Так как напряжение (σ) равно модулю Юнга Е, умноженному на деформацию, то продольная сила, приложенная к стержню:
РEA L
x |
|
x |
|
cos |
y |
|
y |
|
sin , |
(4.3) |
3 |
|
|
2 |
|
3 |
|
|
2 |
|
|
где А – площадь поперечного сечения стержня.
Компоненты продольной силы Р могут быть приравнены к компонентам шарнирных сил и уравнение (1) примет вид:
|
|
|
Fx2 |
P cos |
|
|
|
e |
F |
Fy |
2 |
P sin |
|
F |
2 |
|
|
(4.4) |
||
6 |
F3 |
Fx |
|
P cos |
||
|
|
|
|
|||
|
|
|
3 |
|
|
|
|
|
|
Fy |
|
P sin |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
74 |
|

Подстановка Р из уравнения (4.3) в выражение для Fx2 в уравнении (4) дает:
|
|
EA |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
(4.5, а) |
Fx |
|
|
x |
x cos |
y |
|
|
|
y sin cos |
|||||||||||
|
L |
|
|
|
|
|
||||||||||||||
|
2 |
|
3 |
|
|
2 |
|
|
|
|
|
|
3 |
|
2 |
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fx2 |
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 |
|
|
|
|
|
sin |
cos |
|
|
|
|
(4.5, б) |
||||
|
|
|
|
|
|
x2 |
|
y2 |
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
cos |
|
|
x3 |
sin |
cos |
|
y3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В матричной форме уравнение (4.5, б) имеет вид:
Fx2 |
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
cos2 |
,sin |
|
cos |
, cos2 |
, |
sin |
|
cos |
|
|
|
|
(4.5, в) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Четыре уравнения типа (4.5, в) для |
Fx |
|
,Fy |
|
,Fx |
,Fy |
в мат- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
3 |
|
3 |
|
ричной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F e6 EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 |
, sin cos , |
cos2 |
, |
sin |
cos |
|
|
|
|
|
|
|||||||||
|
|
|
|
x2 |
|
|
|||||||||||||||
|
sin |
cos |
, sin |
2 |
, |
sin |
cos |
, |
sin |
2 |
|
|
|
|
|
|
(4.6, а) |
||||
|
|
|
|
|
y2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
cos2 , |
sin |
|
cos |
, cos2 |
, sin |
cos |
|
|
|
|
|
|
||||||||
|
|
|
|
|
x3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
cos , |
sin2 |
, sin |
cos |
, sin2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
y3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
75
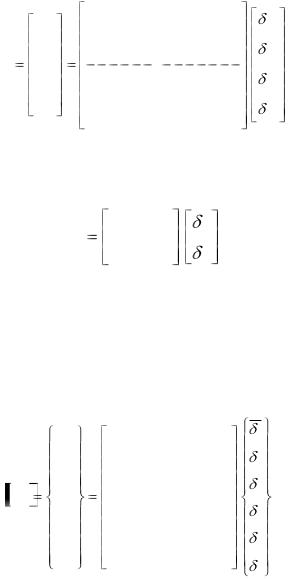
С множителем EAL , внесенным в квадратную матрицу,
уравнение (4.6, а) приобретает вид:
|
|
K x |
,x |
2 |
Kx |
,y |
2 |
| K x |
,x |
K x |
,y |
3 |
|
|
|||
|
|
|
|
||||||||||||||
|
Fx2 |
2 |
|
2 |
|
2 |
|
3 |
2 |
|
|
x2 |
|
||||
|
K y |
|
|
K y |
|
|
|
| K y |
|
|
K y |
|
|
|
|
||
|
Fy2 |
,x |
2 |
,y |
2 |
,x |
,y |
3 |
|
|
|||||||
|
2 |
|
2 |
|
|
2 |
|
3 |
2 |
|
|
|
|
||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
(4.6, б) |
|
F |
6 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
||
|
Fx3 |
K x ,x |
|
K x ,y |
|
|
| K x ,x |
|
K x |
|
|
|
x |
|
|||
|
|
|
|
|
|
y |
|
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
Fy3 |
3 |
|
2 |
3 |
|
2 |
3 |
|
3 |
3, |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
K y |
|
|
K y |
|
|
|
| K y |
|
|
K y |
|
|
|
y3 |
|
|
|
|
,x |
2 |
,y |
2 |
,x |
,y |
3 |
|
||||||||
|
|
3 |
|
3 |
|
3 |
|
3 |
3 |
|
|
|
|
||||
Если матрицы разбиты штриховыми линиями, то уравнение (4.6, б) можно записать следующим образом:
|
K22e6 |
K23e6 |
|
|
e |
2 |
|
||
F |
6 |
|
|
(4.6, в) |
|
K32e6 |
K33e6 |
3 |
|
Уравнение (4.6, в) является матричным уравнением для элемента е6 и его квадратная матрица коэффициентов [К] называется матрицей жесткости элемента. Подобные уравнения могут быть получены и для других элементов. Уравнение (4.6, в) может быть расширено так, чтобы оно включало все узловые смещения системы:
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
F e6 |
0 K e6 |
K e6 |
0 0 |
0 |
|
|
||
|
|
2 |
|
|||||||
|
|
2 |
|
22 |
23 |
|
|
|
|
|
|
e |
F e6 |
0 K e6 |
K e6 |
0 0 |
0 |
3 |
|
||
F |
6 |
3 |
|
32 |
33 |
|
|
|
|
(4.6, г) |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
5 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
6 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
76 |
|
|
|
|
|
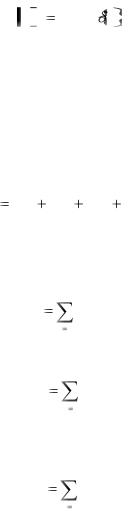
Уравнение (4.6, г) представляет собой расширенное матричное уравнение для элемента е6:
|
|
|
|
F e6 [ |
|
e6 ] |
(4.6, д) |
|
|
|
|
|
K |
||||
|
|
e6 |
|
- расширенная матрица жесткости элемента е6, {δ} |
||||
[K |
] |
|||||||
|
||||||||
– вектор узловых перемещений системы.
Внешние силы R1, R2, …R6 могут быть выражены через
х–у компоненты Rx1 , Ry1 , Rx2 , Ry2 ... Rx6 , Ry6 , а условия равновесия в узловых точках могут быть определены через эти компоненты. Например, в узле с номером 2 условия равновесия в направлении х имеет вид:
R |
F e1 |
F e4 |
F e5 |
F e6 . |
(4.7) |
x2 |
x2 |
x2 |
x2 |
x2 |
|
Хотя в правую часть равенства (4.7) дают вклад только те элементы, которые содержат узел 2, удобно записать это соотношение в общем виде:
|
7 |
|
|
|
Rx2 |
F ei |
, |
(4.8, а) |
|
x2 |
||||
|
i |
1 |
|
|
или |
|
|
|
|
|
|
7 |
|
|
R |
x2 |
F e |
|
(4.8, б) |
|
x2 |
|
|
|
|
e |
1 |
|
|
Аналогичное соотношение получается для другой компоненты вектора R2:
|
7 |
|
|
R |
y2 |
F e . |
(4.8, в) |
|
y2 |
|
|
|
e |
1 |
|
Уравнения (4.8, б) и (4.8, в) можно объединить в матричной записи:
77

|
Rx2 |
|
e |
|
|
|
|
7 |
Fx2 |
7 |
|
||
|
|
|
|
|
||
R |
|
|
|
|
F e . |
(4.9) |
2 |
Ry |
|
|
F e |
2 |
|
|
2 |
e 1 |
e 1 |
|
||
|
|
|
y2 |
|
|
|
Аналогичные уравнения могут быть записаны и для других узлов. Результирующая система уравнений равновесия записывается в виде:
|
R |
|
F e |
|
|
|
1 |
|
1 |
|
|
|
R2 |
7 |
e |
7 |
|
R |
|
F2 |
F e . |
(4.10) |
|
|
|
e 1 |
|
e 1 |
|
|
R6 |
|
F e |
|
|
|
|
|
6 |
|
|
Подстановка выражений типа (4.6, д) в уравнение (4.10)
дает:
7 |
|
|
e . |
|
R |
|
K |
(4.11) |
|
e |
1 |
|
|
|
или |
|
|
|
|
K |
= R |
(4.12) |
||
Это уравнение называется матричным уравнением системы, а матрица К, задаваемая равенством:
7 |
|
|
e |
|
K |
|
K |
(4.13) |
|
e |
1 |
|
|
|
называется матрицей жесткости системы.
Процедура, использованная выше для объединения матричных уравнений элементов, называется поэлементным объединением. Метод анализа конструкций, описанный выше, называется методом перемещений и может быть распространен на случаи:
а) начальных конструкционных (сборочных) или тепловых деформаций,
б) массовых сил, таких, как гравитационные,
78
