
2448
.pdf
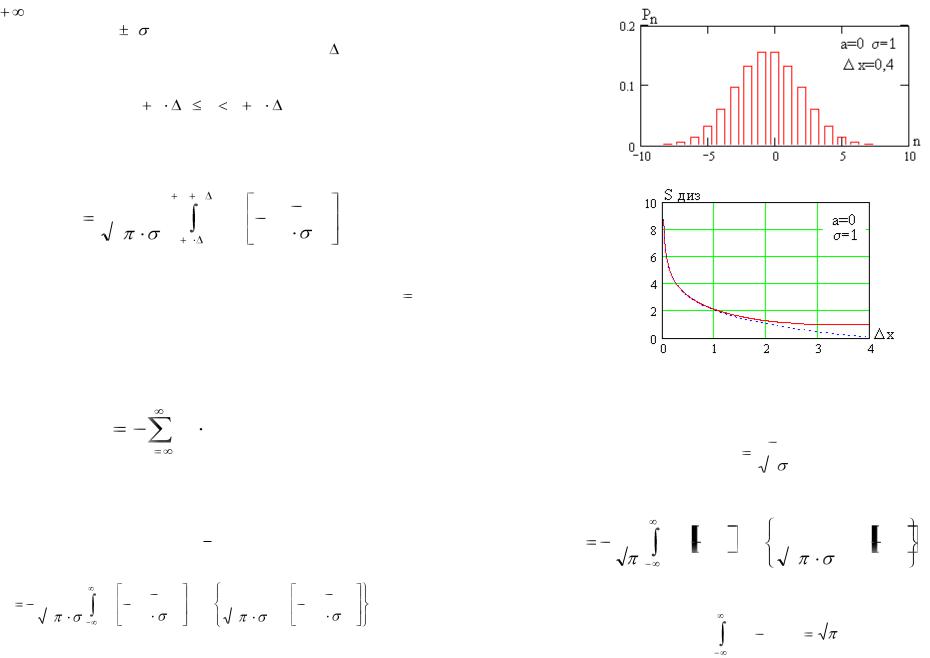
ется, а если величина этого отклонения по модулю становится больше 3 , то плотность вероятностей становится близкой к нулю (в теории вероятностей этот результат называют «законом 3 »).
Рис. 8.2
На рис. 8.3 представлены зависимости функции распределения вероятностей F(x) для различных средних значений
a и СКО . При увеличении a кривая смещается вправо, а с ростом СКО становится более пологой.
Рис. 8.3
79
8.3. Скрытность состояний с непрерывным множеством значений
Рассмотрим скрытность состояний с непрерывным множеством безразмерных значений от в интервале от x1 до x2 .
Разобьем его на N отрезков |
|
x , |
|
||||
x |
|
|
x2 |
x1 |
, |
(8.8) |
|
|
|
|
N |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
тогда на n -м отрезке ( n |
1, N ) значения состояния будут на- |
||||||
ходиться в границах от x1 |
|
|
(n |
1) x до x1 |
n x . Такие про- |
||
цедуры называют квантованием непрерывной переменной, а
величину |
x - шагом квантования. |
|
|
||
Согласно (8.5) вероятность попадания значения состояния |
|||||
в n -й интервал будет конечной величиной, равной |
|
||||
|
|
x1 |
n x |
|
|
|
Pn |
|
w( x)dx . |
(8.9) |
|
|
x1 |
( n |
1) |
x |
|
При малых |
x приближенно можно записать |
|
|||
|
Pn |
w(xn ) |
x , |
(8.10) |
|
где xn - значение состояния, соответствующее n -му интервалу, например, его середине,
x |
x |
(2n 1) |
x . |
(8.11) |
|
||||
n |
1 |
2 |
|
|
|
|
|
|
Потенциальная (энтропийная) скрытность согласно (5.17) определяется выражением
80

N |
|
|
S |
Pn log2 Pn . |
(8.12) |
n |
1 |
|
Подставляя (8.10) и учитывая свойство логарифма произведения, получим
N |
|
|
|
N |
|
|
|
S |
w(xn ) |
x log2[w(xn )] |
|
w(xn ) |
x log2 ( |
x) , |
(8.13) |
n |
1 |
|
|
n 1 |
|
|
|
а после преобразования запишем (8.13) в виде |
|
|
|||||
N |
|
|
|
|
N |
|
|
S |
w(xn ) |
log2[w(xn )] |
x |
log2 ( x) |
w(xn ) |
x . |
(8.14) |
n |
1 |
|
|
|
n 1 |
|
|
Переходя к пределу при |
x |
0 (шаг квантования при |
|||||
этом становится дифференциалом переменной интегрирования dx ) и заменяя суммы интегралами, с учетом (8.3) получим
|
x2 |
|
|
|
|
S |
w(x) |
log2 [w(x)]dx lim log |
2 ( x) . |
(8.15) |
|
|
x1 |
x 0 |
|
|
|
|
|
|
|
||
|
Как видно, интеграл |
|
|
||
|
|
|
x2 |
|
|
|
|
S |
w(x) log2 [w(x)]dx . |
(8.16) |
|
|
|
|
x1 |
|
|
определяет зависимость потенциальной скрытности от вероятностных характеристик (плотности вероятностей) непрерывных значений состояния, а второе слагаемое в (8.15) ха81
рактеризует только процедуру квантования (оно стремится к бесконечности при x 0 ).
Так как распределение вероятностей характеризует раз-
брос значений состояния в заданном диапазоне, то S вида
(8.16) целесообразно назвать скрытностью рассеивания.
Она позволяет проводить сравнительный анализ скрытности объектов с различными распределениями вероятностей состояний.
Величину |
|
|
S |
log2 ( x) |
(8.17) |
можно назвать скрытностью дискретизации. Она зависит только от требуемой точности, с которой должно быть определено значение состояния (чем меньше погрешность, тем
больше S ).
В целом скрытность (8.15) состояний с непрерывными значениями всегда бесконечна. При заданном шаге дискретизации x она оказывается конечной и определяется выражением (8.12), а вероятности Pn вычисляются в соответствии с
(8.9) и зависят как от x , так и плотности вероятностей w(x) значений состояния.
8.4.Скрытность состояний с равномерной плотностью вероятностей значений
Пусть значения |
x состояния в диапазоне от x1 до x2 |
|||
( x2 x1 D ) имеют |
равномерную плотность |
вероятностей |
||
вида |
|
|
|
|
|
w(x) |
1 |
, |
(8.18) |
|
|
|||
|
|
D |
|
|
82
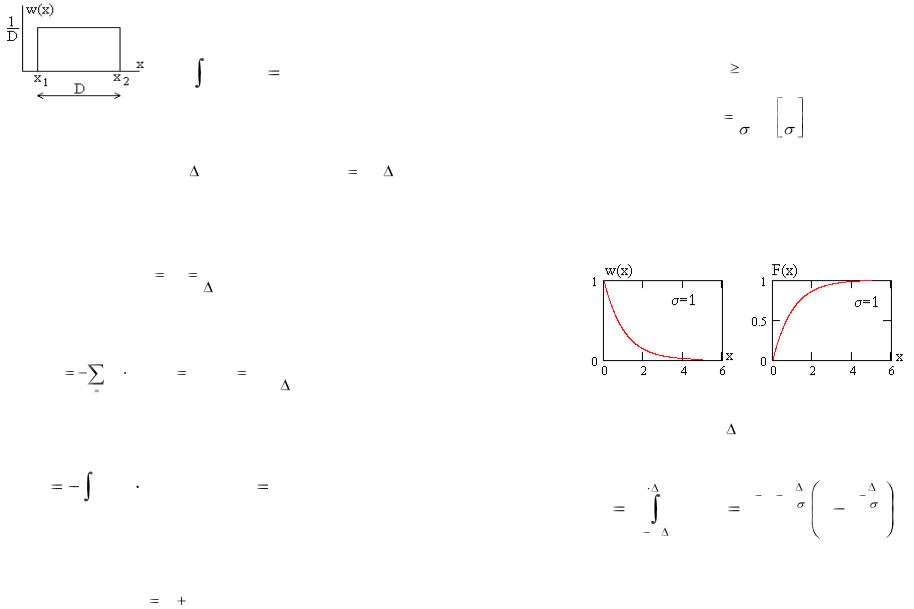
как показано на рис. 8.4. Очевидно, что выполняется условие
x2 |
|
w(x)dx 1 . |
(8.19) |
x1 |
|
Рис. 8.4 |
|
Пусть шаг дискретизации x выбран так, что N |
D / x |
является целым числом ( N - число одинаковых интервалов дискретизации), тогда вероятность попадания в него значения состояния согласно (8.9) равна
|
|
|
|
P |
1 |
|
|
|
|
D |
. |
|
|
|
(8.20) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
n |
|
|
N |
|
|
|
|
x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Определим потенциальную скрытность (8.12) состояния |
|||||||||||||||||||||
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
S |
P |
log |
P |
|
log N log |
. |
(8.21) |
||||||||||||
|
|||||||||||||||||||||
|
|
|
n |
2 |
|
n |
2 |
|
|
2 |
x |
|
|||||||||
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
При этом скрытность рассеивания S из (8.16) равна |
|
||||||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
w(x) log2 [w(x)]dx |
log2 D , |
(8.22) |
|||||||||||||||||
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
а скрытность дискретизации |
S определяется из (8.17). Оче- |
||||||||||||||||||||
видно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
S |
S . |
|
|
|
(8.23) |
||||||||||
|
|
|
|
|
83 |
|
|
|
|
|
|
|
|
|
|||||||
8.5. Скрытность состояний с показательной плотностью вероятностей значений
Плотность показательного (экспоненциального) распре-
деления вероятностей при x |
0 имеет вид |
|
|||
w(x) |
1 |
exp |
x |
. |
(8.24) |
|
|
||||
Параметр 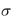 - среднее значение и среднеквадратическое отклонение (в данном случае они совпадают). График плотности вероятностей w(x) показан на рис. 8.5, а на рис. 8.6 – со-
- среднее значение и среднеквадратическое отклонение (в данном случае они совпадают). График плотности вероятностей w(x) показан на рис. 8.5, а на рис. 8.6 – со-
ответствующей функции распределения вероятностей F(x) .
Рис. 8.5 |
|
Рис. 8.6 |
|
|
||
При шаге квантования |
x вероятность попадания значе- |
|||||
ния состояния в n -й интервал согласно (8.5) равна |
||||||
n |
x |
e ( n 1) |
x |
x |
||
Pn |
w(x)dx |
|
1 e |
|
|
|
|
. (8.25) |
|||||
(n |
1) x |
|
|
|
|
|
Из (8.12) получим выражение для потенциальной скрытности
84
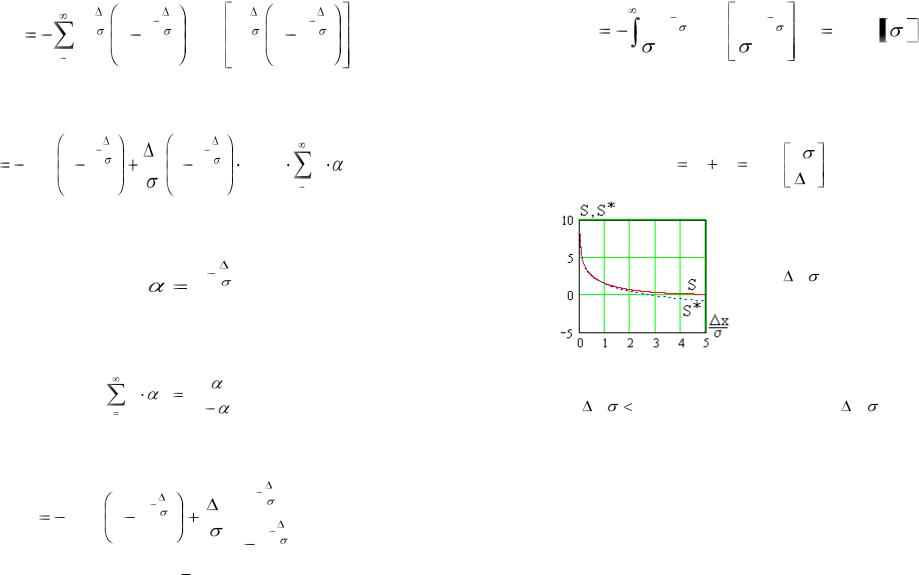
|
|
n |
x |
|
x |
|
n |
x |
|
x |
|
S |
e |
|
1 e |
log2 e |
|
1 e |
, (8.26) |
||||
|
|
|
|
||||||||
n0
апосле алгебраических преобразований можно записать
|
|
x |
x |
|
|
x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
S |
log2 1 e |
|
1 e |
|
|
|
log2 e |
n |
||||
|
|
|
|
|
, (8.27) |
|||||||
|
|
|
|
|
|
|
|
|
|
n |
0 |
|
где введено обозначение |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
(8.28) |
||||
Сумма в правой части (8.28) является арифметикогеометрической прогрессией и равна
n |
n |
|
|
|
. |
(8.29) |
(1 |
) |
2 |
||||
n 0 |
|
|
|
|||
С учетом этого из (8.27) после преобразований получим
|
|
|
|
|
|
|
|
x |
|
|
|
|
S |
log2 1 e |
x |
|
x |
e |
|
log2 e . (8.30) |
|||||
|
|
|
||||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x |
|
|||
|
|
|
1 |
e |
|
|
||||||
Скрытность рассеивания S согласно (8.16) равна
85
|
|
1 |
|
x |
1 |
|
x |
|||
|
|
|
|
|
e |
|
|
|||
S |
0 |
e log2 |
|
dx log2 e , (8.31) |
||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||
скрытность квантования определяется (8.17), а полная скрытность при малом шаге квантования определяется выражением
|
S* |
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
S S log2 |
. |
|
(8.32) |
|||||||
|
|
|
|
|
|||||||
|
|
x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
На рис. 8.7 представлены |
||||||
|
|
|
|
|
зависимости S и S* от нор- |
||||||
|
|
|
|
|
мированного шага |
квантова- |
|||||
|
|
|
|
|
ния |
|
x / . |
|
Уменьшение шага |
||
|
|
|
|
|
квантования приводит к по- |
||||||
|
|
|
|
|
вышения |
|
скрытности. Как |
||||
|
|
|
|
|
видно, выражение (8.32) хо- |
||||||
|
|
|
|
|
рошо согласуется с точным |
||||||
|
Рис. 8.7 |
|
|
|
выражением для определения |
||||||
|
|
|
|
|
скрытности вида (8.30) в об- |
||||||
ласти x / |
1. При больших величинах |
x / |
возникают |
||||||||
сильные расхождения (величина S* |
может стать даже отрица- |
||||||||||
тельной), так как выражение для S* получено при условии малости шага квантования.
8.6.Скрытность состояний с нормальной плотностью вероятностей значений
Нормальное (гауссовское) распределение вероятностей непрерывной случайной величины в качестве примера рассмотрено в параграфе 8.2. Ее плотность вероятностей определяется выражением (8.7), графики показаны на рис.8.1 и 8.2.
Диапазон изменения значений x состояния от  до
до
86
, однако фактически они с высокой вероятностью нахо-
дятся в пределах 3 |
от среднего значения a . |
|
Пусть квантование производится с шагом |
x в обе сто- |
|
роны от a , тогда n -й интервал квантования имеет вид |
||
a |
n x x a n x . |
(8.33) |
Вероятность попадания в него значения состояния согласно
(8.9) равна
|
|
|
1 |
|
a (n 1) x |
(x a)2 |
||||
|
|
|
|
|
|
|||||
Pn |
|
|
|
|
|
exp |
|
|
|
dx . (8.34) |
|
|
|
|
|
2 |
2 |
|
|||
2 |
|
|
|
|||||||
|
|
|
|
a n |
x |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
Интеграл (8.34) не берется, то есть не выражается в эле- |
||||||||||
ментарных функциях. Пример зависимости Pn |
от n при a 0 |
|||||||||
показан на рис. 8.8. Как видно, высоко вероятными являются значения состояния, близкие к среднему значению a .
Потенциальная скрытность определяется выражением, подобным (8.12),
S |
Pn log2 Pn , |
(8.35) |
|
n |
|
где вероятности |
Pn определяются из (8.34). Зависимость по- |
|
тенциальной скрытности от шага квантования показана сплошной линией на рис. 8.9.
Скрытность рассеивания S согласно (8.16) равна
|
1 |
|
|
(x a)2 |
|
|
1 |
|
|
(x a)2 |
dx .(8.34) |
|||||
S |
|
exp |
log2 |
|
|
exp |
||||||||||
|
|
|
|
2 |
2 |
|
|
|
2 |
2 |
||||||
2 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
87 |
|
|
|
|
|
|
|
|
Рис. 8.8
|
Рис. 8.9 |
|
|||||
Используя замену переменной |
|
||||||
z |
|
x |
|
a |
, |
(8.35) |
|
|
|
|
|
||||
2 |
|||||||
|
|
|
|
||||
получим
|
|
1 |
|
exp z 2 log2 |
|
|
1 |
|
|
|
|
z 2 dx . (8.36) |
||
S |
|
|
|
|
|
|
exp |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя известные значения интегралов |
|
|||||||||||||
|
|
|
|
|
|
exp( z2 )dz |
|
|
|
|
|
|||
|
|
|
|
|
|
|
, |
(8.37) |
||||||
|
|
|
|
|
88 |
|
|
|
|
|
|
|
||
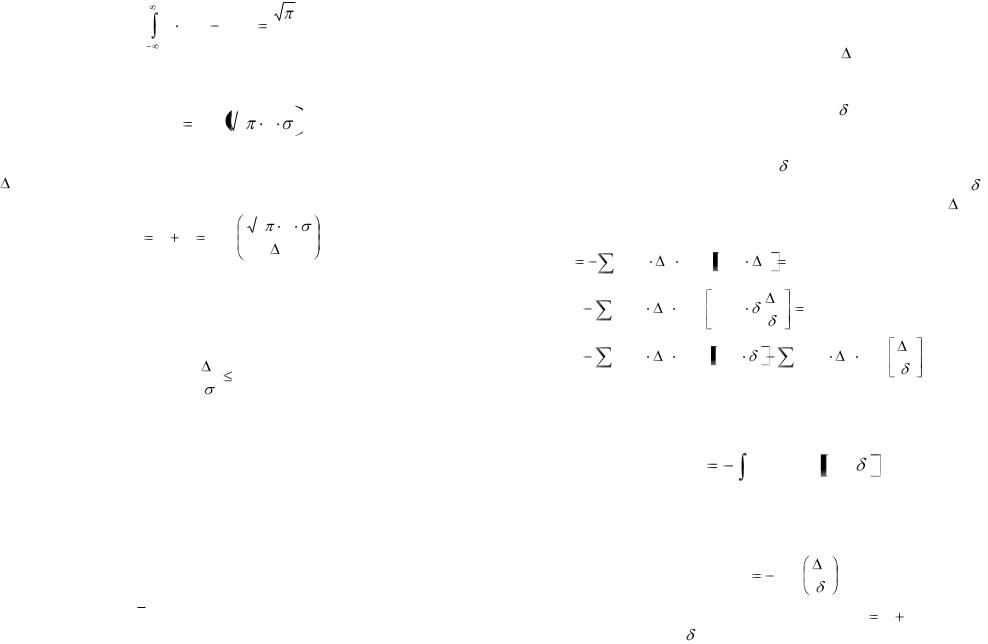
|
z2 |
exp( z2 )dz |
|
|
|
|
|
|
|
||||||||
2 |
, |
|
(8.38) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
получим простое выражение |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
S |
|
|
|
log2 2 |
e |
. |
|
(8.39) |
||||||
С учетом скрытности |
квантования |
(8.17) при |
малых |
||||||||||||||
x приближенно получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
e |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
S S |
S |
log2 |
|
|
|
|
|
. |
(8.40) |
||||||||
|
|
|
x |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зависимость (8.40) от шага квантования показана на рис. 8.9 пунктирной линией. Как видно, она хорошо аппроксимирует точное выражение (8.35) при ранее полученном условии
|
x |
1. |
(8.41) |
|
|
||
|
|
||
8.7. Проблема размерности значений состояния |
|||
До сих пор полагалось, что значения x |
состояния безраз- |
||
мерны. Однако на практике часто приходится иметь дело с физическими значениями состояния (длина, вес, частота).
При определении потенциальной скрытности трудности не возникают, так как аргумент плотности вероятностей w(x)
всегда относится к константе, имеющей ту же размерность, например, к среднеквадратическому отклонению.
Проблема появляется при необходимости анализа скрыт-
ности рассеивания S (8.16), так как плотность вероятности, являющаяся аргументом логарифмической функции, имеет
89
размерность, обратную x , что недопустимо. |
Это же относит- |
|||
|
|
|
|
|
|
|
|
|
|
ся и к скрытности дискретизации S (8.17), |
где необходимо |
|||
вычислять логарифм шага квантования x , |
размерность ко- |
|||
торого совпадает с x .
Выход заключается в нормировании шага дискретизации делением его на некоторую константу , которую назовем квантом значения состояния, его размерность равна x , а значение может выбираться из технических или иных сооб-
ражений. Например, в качестве |
|
можно использовать мини- |
|||||||
мально достижимую погрешность измерения. Величина |
|||||||||
может быть как больше, так и меньше шага квантования |
x . |
||||||||
|
Из (8.10) и (8.12) получим |
|
|
|
|
|
|||
S |
w(x) |
x log2 |
w(x) x |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
w(x) |
x log2 |
w(x) |
|
x |
|
|||
|
|
|
. |
(8.42) |
|||||
|
|
|
|||||||
|
n |
|
|
|
|
|
|
|
|
|
w(x) |
x log2 |
w(x) |
|
w(x) x log2 |
x |
|
||
|
|
|
|
|
|||||
|
|
|
|
||||||
|
n |
|
|
|
|
n |
|
||
Тогда по аналогии с (8.13) – (8.15) получим выражение для скрытности рассеивания
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
S |
|
w(x) log2 |
w(x) |
dx , |
(8.43) |
|||||||
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
и скрытности дискретизации |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
. |
|
|
|
(8.44) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
S |
log |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потенциальная скрытность как сумма S |
S |
S (8.23) не |
||||||||||
зависит от кванта .
90

Если  x , то скрытность дискретизации S имеет смысл минимального среднего числа двоичных измерений, необходимых для локализации значения состояния в одном
x , то скрытность дискретизации S имеет смысл минимального среднего числа двоичных измерений, необходимых для локализации значения состояния в одном
их интервалов |
x внутри кванта . С ростом |
она увеличи- |
|
вается, при |
x становится равной нулю, |
а при |
x |
оказывается отрицательной (в этом случае не требуется локализации интервала квантования).
При изменении S на ту же величину, но в обратном на-
правлении, меняется скрытность рассеивания S , так, что их сумма остается постоянной согласно (8.23).
Особый интерес представляет выбор величины кванта,
равной |
|
|
x . |
(8.45) |
|
|
|
|
|
|
|
При этом скрытность дискретизации равна нулю ( S |
0 ), а |
|
скрытность рассеивания S совпадает с потенциальной скрытностью S .
8.8. Пример анализа скрытности состояний с непрерывными значениями
Рассмотрим задачу поиска сигнала радиостанции с неизвестной частотной настройкой в заданном диапазоне частот от f1 до f2 . Очевидно, что для абсолютно точного решения
задачи потребуется измерительная процедура бесконечной продолжительности.
На практике точность любых измерений ограничена как возможностями аппаратуры, так и практической целесообразностью. В рассматриваемом случае минимальное значение допустимой ошибки поиска сигнала по частоте обусловлена, например, собственной нестабильностью частоты сигнала радиопередатчика, влиянием ошибки измерения на качество
91
приема искомого сигнала и т.д.. Плотность вероятностей w( f ) рабочей частоты f может иметь различный вид.
Если устройство разведки частотного диапазона не располагает какими либо сведениями о рабочей частоте искомого сигнала, то целесообразно использовать равномерную плотность вероятностей вида (8.18) и рис. 8.4.
При наличии сведений о стремлении передатчика занимать частоты прежде всего в нижней части диапазона (ближе
кf1 ) можно принять показательную (экспоненциальную)
плотность вероятностей вида (8.24) и рис. 8.5.
В различных технических задачах часто возникает нормальная (гауссовская) плотность вероятностей (8.7) и рис. 8.1. В рассматриваемой задаче оно может возникнуть, если доллжна выбираться возможно ближе к некоторой центральной (средней) частоте f0 , а возникающие отклонения обусловле-
ны большим числом влияющих на это факторов.
При сравнении различных вероятностных законов необходимо задать одинаковые условия. В качестве базиса сравнения при для плотностей вероятностей с ограниченным и бесконечным диапазоном изменения целесообразно выбрать среднеквадратическое отклонение (СКО) , которое в данном случае измеряется в единицах частоты. Обозначим шаг дискретизации частоты через f .
Для равномерной плотности вероятностей СКО равно
|
|
D |
|
. |
(8.46) |
|
|
|
|
|
|||
12 |
||||||
|
|
|||||
В этом случае потенциальная скрытность SР |
согласно (8.21) |
|||||
равна |
|
|||||
|
|
12 |
|
|
|
|
|
|
|
|
SР |
log2 |
log2 |
|
log2 12 log2 |
|
1,792 |
. (8.47) |
|||
|
|
|
||||||||
|
|
|
||||||||
|
|
f |
|
f |
|
|
|
f |
|
|
92
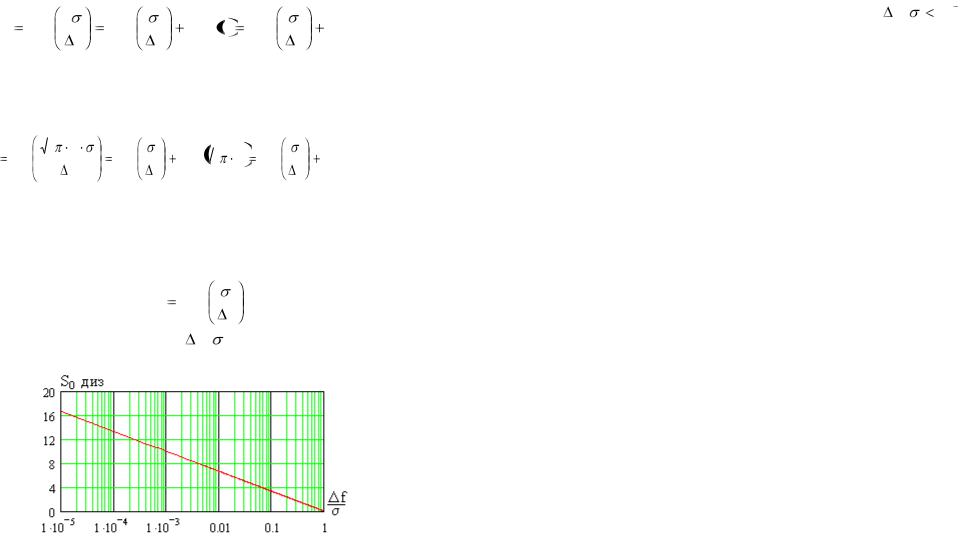
Для показательной плотности вероятностей для расчета скрытности SП воспользуемся приближенным соотношением
(8.32) при условии (8.41),
SП |
log2 |
e |
|
log2 |
|
|
log2 e |
|
log2 |
|
|
|
1,443. (8.48) |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
f |
|
|
|
f |
|
|
|
|
|
f |
|||||
|
Потенциальная скрытность |
SН |
при нормальной плотно- |
||||||||||||||||
сти вероятностей определяется из (8.40), |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
SН |
log2 |
|
|
log2 |
|
|
|
log2 |
2 |
e log2 |
|
|
2,047. (8.49) |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
f |
|
|
|
f |
|
|
|
|
|
f |
|||||
Как видно из (8.47) – (8.49), для различных плотностей вероятностей потенциальная скрытность определяется величиной
S0 |
log2 |
|
. |
(8.50) |
|
||||
|
|
f |
|
|
Зависимость S0 от величины |
f / |
показана на рис. 8.10. |
||
Рис. 8.10
93
Для равных СКО наибольшее значение потенциальной скрытности обеспечивается для нормальной плотности вероятностей. Скрытность при равномерной плотности примерно на 0,255 диз меньше, а при показательной – на 0,604 диз.
При малом шаге дискретизации частоты f / |
10 3 |
скрытность практически одинакова для всех рассмотренных плотностей вероятностей.
94
Глава 9. АРСЕНАЛЬНАЯ СКРЫТНОСТЬ СИГНАЛОВ РАЗЛИЧНОЙ СТРУКТУРЫ
9.1. Разнообразие сигналов и арсенальная скрытность
Трудно перечислить в коротком обзоре все сигналы, применяемые в настоящее время для передачи информации разного назначения в различных системах связи, частотных диапазонах, условиях распространения и помехах. Широкое распространение получили сигналы с цифровой структурой при соответствующих методах их формирования и обработки.
Арсенальной будем называть скрытность, определяемую мощностью A (числом элементов) множества X возможных сменных параметров сигнала, например, несущих частот, вариантов кодовой структуры. Рабочие параметры передаваемого сигнала выбираются из этого множества случайно для противника.
Радиосигналы принято делить на две категории – узкополосные (УПС) и широкополосные (ШПС). Узкополосными
называют радиосигналы с базой |
B (произведением ширины |
||||||||||
спектра F на длительность T ), соизмеримой с единицей, |
|||||||||||
|
|
|
B |
|
FT |
1. |
(9.1) |
||||
Широкополосными называют сигналы, для которых |
|
||||||||||
|
|
|
B |
FT |
1 . |
(9.2) |
|||||
Введем понятие базы передатчика |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B FT , |
(9.3) |
||||||
|
|
|
|
||||||||
где T - максимальная длительность сигналов из множества |
|||||||||||
|
|
|
|
||||||||
X , а F - диапазон частот, в котором могут находиться |
рабо- |
||||||||||
чие сигналы. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
95 |
|
|
|
||||
9.2. Арсенальная скрытность узкополосных сигналов
Примем в качестве образца узкополосного сигнала отрезок гармонического колебания длительностью T с прямо-
угольной огибающей и варьируемой в диапазоне F частотой при постоянной начальной фазе.
Ширина спектра такого сигнала определяется известным
соотношением |
|
|
|
F |
1 |
. |
(9.4) |
|
|||
|
T |
|
|
При базе передатчика (9.3) возможное число не перекрывающихся по частоте каналов (их арсенал) равно
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
A |
|
FT . |
(9.5) |
||||
|
|
|
|||||
F |
|
||||||
|
|
|
|
|
|
||
Если T T , то получим
|
|
|
|
|
|
|
|
A FT B , |
(9.6) |
||||||
то есть арсенал частотных каналов равен базе передатчика.
Примем, что рабочий сигнал xi , i |
|
|
|
1, A , выбирается из |
|||
имеющегося арсенала с равными вероятностями |
|||
pi 1/ A . |
(9.7) |
||
При этом условии потенциальная арсенальная скрытность (А-скрытность) узкополосных сигналов S0 определяется выражением
|
|
|
|
S0 log2 (1/ A) log2 A log2 (FT ) . |
(9.8) |
||
96
9.3. Широкополосные сигналы и их скрытность
9.3.1. Широкополосные сигналы на базе двоичных последовательностей
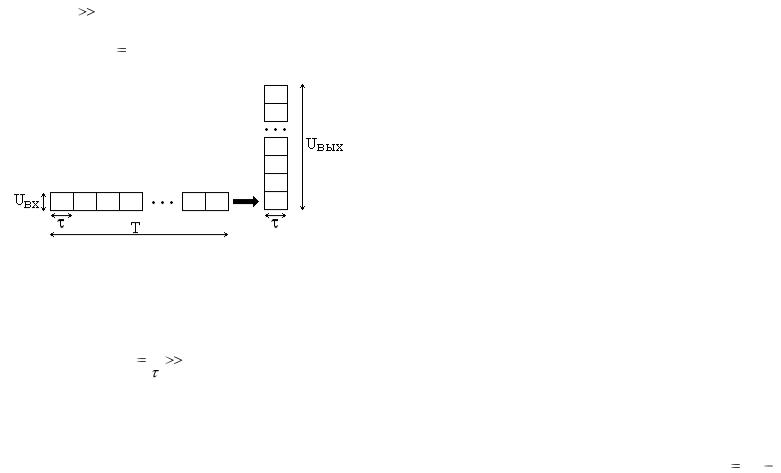
На практике широкополосные информационные сигналы часто представляют собой двоичную импульсную последовательность из M 1 элементов с длительностью элементарного двоичного символа (микроимпульса) 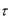 и общей длительностью сигнала T M
и общей длительностью сигнала T M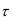 , как показано на рис. 9.1.
, как показано на рис. 9.1.
Рис. 9.1
Ширина спектра такого ШПС определяется длительностью микроимпульса 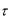 , обычно оценивается величиной
, обычно оценивается величиной
F |
1 1 |
, |
(9.9) |
||
|
|
T |
|||
|
|
|
|
|
|
и много больше ширины спектра узкополосного сигнала длительностью T .
Структура кодовых последовательностей выбирается таким образом, чтобы при заданном их числе (арсенале) A обеспечить их максимальное взаимное различие, мерой которого являются взаимокорреляционные функции (ВКФ).
На приемной стороне широкополосного канала связи при97
нятый ШПС в смеси с помехами сравнивается со всеми копиями передаваемых сигналов с помощью вычисления значений ВКФ, по максимуму которых выбирается переданный информационный сигнал. Для получения ВКФ используются корреляторы или согласованные фильтры, настроенные на заданный ожидаемый ШПС, в которых поступающие микроимпульсы накапливаются (складываются или вычитаются) в соответствии с кодовой структурой ШПС.
В устройстве обработки, настроенном на принимаемый сигнал, происходит сложение амплитуд UВХ входных микроимпульсов, образуя отклик с амплитудой UВЫХ длительно-
стью 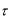 , как показано на рис. 9.1, а отсчеты помехи всегда накапливаются несогласованно. В результате, даже если амплитуда входного сигнала ниже уровня помех (сигнал «тонет» в помехах), амплитуда отклика на выходе устройства обработки ШПС может быть выше помеховой компоненты, обеспечивая достоверный прием сигнала. Качество приема тем выше, тем лучше корреляционные свойства арсенала ШПС.
, как показано на рис. 9.1, а отсчеты помехи всегда накапливаются несогласованно. В результате, даже если амплитуда входного сигнала ниже уровня помех (сигнал «тонет» в помехах), амплитуда отклика на выходе устройства обработки ШПС может быть выше помеховой компоненты, обеспечивая достоверный прием сигнала. Качество приема тем выше, тем лучше корреляционные свойства арсенала ШПС.
На практике ШПС на базе двоичных последовательностей чаще всего используются в радиоканалах с фазовой (ФМ) и относительной фазовой (ОФМ) модуляцией.
9.3.2. ШПС на базе М-последовательностей
Двоичные последовательности максимальной длины или М-последовательности широко используются в технике связи. Они формируются на основе двоичных регистров сдвига с линейными обратными связями. Если используется регистр, содержащий m разрядов, то с его помощью может быть сформирована псевдослучайная двоичная последовательность длиной M элементов,
M 2m 1 . |
(9.10) |
Это максимально возможное значение длины неповторяющегося двоичного кода, чем и обусловлено их название.
98
