
1594
.pdf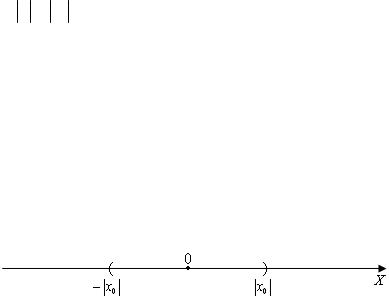
Сравним ряд (2.6) с рядом, составленным из членов геометрической прогрессии:
|
|
|
|
|
|
|
|
|
|
x |
|
|
M |
|
|
x |
|
|
2 |
|
|
x |
|
|
n .... |
|
|||
|
|
|
|
|
|
|
|
|
M M |
|
|
|
|
... M |
|
|
(2.7) |
||||||||||||
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
x |
|
|
то | q | 1, |
|
|||||||||||||||||||||
Поскольку q |
|
|
, |
и потому ряд (2.7) сходится. Ряды (2.6) и (2.7) |
|||||||||||||||||||||||||
x0 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
положительные, |
|
и |
потому |
|
|
к |
ним |
|
|
|
применим |
признак сравнения. Т.к. |
|||||||||||||||||
|
a |
xn |
|
M для n 0, |
1, 2,... , то ряд (2.6) также будет сходиться, а значит, бу- |
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дет сходиться и ряд (2.5), причём абсолютно. Отсюда следует, что ряд (2.3) будет абсолютно сходиться для всех x таких, что | x | | x0 | .
Следствие. Если степенной ряд расходится при x x1 , то он будет расходиться при всех x x1 .
Д о к а з а т е л ь с т в о (от противного). Предположим противное: пусть
ряд расходится при x x1 |
и сходится при некотором x x0 , причём |
|
x0 |
|
|
|
x1 |
|
. |
|
|
|
|
Но тогда по теореме Абеля ряд будет сходиться и при x x1 . Мы пришли к противоречию, которое показывает, что наше предположение неверно. По-
этому ряд расходится при всех |
|
x |
|
|
|
x1 |
|
. |
|
|
|
|
|
|
|
при некотором x x0 , |
||||||||
|
|
|
|
|||||||||||||||||||||
|
|
Таким образом, если степенной |
|
ряд сходится |
||||||||||||||||||||
x0 0 , |
|
то он сходится и при всех |
|
|
x |
|
|
|
x0 |
|
, т.е. |
сходится на интервале |
||||||||||||
|
|
|
|
|
||||||||||||||||||||
( |
|
x0 |
|
; |
|
x0 |
|
) , симметричном относительно начала координат (рис. 2). |
||||||||||||||||
|
|
|
|
|||||||||||||||||||||
Рис. 2. Интервал, на котором сходится степенной ряд, если он сходится в точке x x0 , x0 0
Если же степенной ряд расходится в точке x1 , то он расходится и во всех точках, расположенных вне интервала ( | x1 |;| x1 |).
Сказанное уточняет следующая теорема.
Теорема. Если степенной ряд (2.3) сходится не при всех x и не только при x 0, то существует число R 0 такое, что ряд (2.3) абсолютно сходится
при | x | R и расходится при | x | R.
Д о к а з а т е л ь с т в о. Пусть {x0} множество всех точек x0 , в которых
ряд an xn сходится. Покажем, что множество {x0} ограничено. Пусть в
n 0
точке x1 степенной ряд расходится. Тогда для любого x0 {x0} выполняется
31
неравенство | x0 | | x1 |, из которого следует, что множество {x0} ограничено. Рассмотрим теперь множество {| x0 |}, x0 {x0}. Ясно, что оно ограничено сверху. Пусть R sup{| x0 |}, 0 R . Фиксируем произвольный x, | x | R.
Тогда, по определению точной верхней грани числового множества, найдется точка x0 {x0}такая, что | x | | x0 | R. В силу теоремы Абеля ряд будет абсо-
лютно сходиться в точке x. Фиксируем теперь произвольный x такой, что | x | R.Тогда x {x0}. Действительно, если бы x {x0}, то | x | {| x0 |}, а потому выполнялось бы условие | x | R. Итак, x {x0}, и потому в такой точке x
степенной ряд расходится.
Очевидно, что число R , фигурирующее в теореме, единственно. Интервал ( R; R) называется интервалом сходимости степенного ряда.
Число R называется при этом его радиусом сходимости.
Примем следующие соглашения. Если степенной ряд сходится при всех x E1, то положим R . Если же степенной ряд сходится только при x 0, то положим R 0.
Из доказанной теоремы и принятых соглашений следует. что всякий степенной ряд имеет радиус сходимости.
Заметим, что в точках x R и x R ряд может как сходиться, так и расходиться.
Вычисление радиуса сходимости степенного ряда
Теорема. Если существует конечный предел lim |
an 1 |
0 , то радиус схо- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
an |
|
димости степенного ряда (2.3) вычисляется по формуле |
|
|||||||||||||
|
|
|
|
|
|
an |
|
|
|
|
|
|||
|
|
R lim |
|
|
. |
|
|
|
||||||
an 1 |
|
|
|
|||||||||||
|
|
|
n |
|
|
|
|
|
||||||
|
|
|
|
|
|
an 1 |
|
|||||||
Д о к а з а т е л ь с т в о. Поскольку lim |
|
0 , то обозначим этот предел |
||||||||||||
|
|
|
|
n |
|
an |
|
|
|
|||||
через |
1 |
, R 0, так что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
R |
an 1 |
|
|
|
1 |
|
|
|
|
|
|
||
|
|
lim |
|
|
. |
|
|
|
|
(2.8) |
||||
|
|
|
|
|
|
|
||||||||
|
|
n |
an |
|
|
R |
|
|
|
|
|
|
||
Для нахождения радиуса сходимости степенного ряда воспользуемся обобщённым признаком Даламбера сходимости числовых рядов. Заметим,
32

что любой |
степенной ряд |
сходится |
в точке |
|
x 0 . Полагая |
теперь, что |
||||||||||||||||||||||||||||
x 0, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
an 1 xn 1 |
|
|
|
|
x |
|
|
an 1 |
|
|
|
|
x |
|
|
, |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
так что |
| x | |
. |
|
|
|
|
|
n |
|
an xn |
|
|
|
|
|
|
|
|
n |
an |
|
|
|
|
R |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
R |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поэтому, |
когда |
|
|
|
|
1, |
т.е. при |
|
x |
|
R , |
степенной ряд будет сходиться, |
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
R |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 ). Если же |
|
|
x |
|
|
1, т.е. если |
|||||||||
причем абсолютно (в том числе и в точке |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
R |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x R , то степенной ряд (2.3) будет расходиться. Таким образом, число R
как раз и будет радиусом сходимости степенного ряда. Этот радиус определяется по формуле
R lim an ,
n an 1
следующей из равенства (2.8).
З а м е ч а н и е. Покажем, что если |
lim |
an 1 |
|
, то R 0, |
а если |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
an |
|
|
|
|
|
|
|
|
lim |
|
an 1 |
|
0, то R . |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
n |
|
an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
lim |
|
a |
n 1 |
|
.Фиксируем произвольныйx 0. |
Тогда lim |
|
a |
n 1 |
xn 1 |
|
|
||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
n |
|
an |
|
|
|
|
|
n |
|
|
an xn |
|
|
||
lim |
an 1 |
| x | . |
Используя обобщённый |
признак |
Даламбера, |
получаем, |
|||||||||||||||
n |
an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
что степенной ряд в точке x расходится. Поэтому ряд (2.3) сходится только в точке x 0, и потому R 0.
Пусть теперь lim |
an 1 |
0 . Фиксируем произвольный x 0 . Тогда |
|||||||||||||||
n |
an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
a |
n 1 |
xn 1 |
|
|
|
x |
|
lim |
|
a |
n 1 |
|
0 , |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
xn |
|
|
|
|
|
|
||||||||
|
n |
|
|
an |
|
|
|
|
|
n |
|
an |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
и потому ряд (2.3) будет абсолютно сходиться при любом x 0 . Поскольку, очевидно, ряд (2.3) абсолютно сходится и при x 0 , то он будет сходиться абсолютно x E1, так что R .
33
Из сделанного замечания следует, что формула для определения радиуса
сходимости R справедлива и тогда, когда предел lim |
|
an |
|
равен 0 или . |
|
an 1 |
|||||
n |
|
|
|||
Установим справедливость ещё одной формулы, часто используемой при
нахождении радиуса сходимости степенного ряда an xn .
n 0
Пусть существует предел
lim n | an | L, L 0.
n
Предположим сначала, что 0 L . Применим к степенному ряду обобщённый признак Коши:
|
lim n | an xn | lim |
n | an || xn | lim n | an || x |n |
| x | lim n | an | |
L | x |. |
|||||||||
|
n |
n |
n |
|
|
|
n |
|
|||||
Получаем, что: |
|
1 |
|
|
|
|
|
|
|
|
|||
1) |
если |
L | x | 1, т. е. если | x | |
|
, то ряд сходится, причём абсолютно; |
|||||||||
L |
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
||||
2) |
если же L | x | 1, |
т. е. если | x | |
, то ряд расходится. |
|
|||||||||
|
L |
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
||
Таким образом, в рассмотренном случае |
R |
. |
|
|
|||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
L |
|
|
||
Пусть теперь L 0. В этом случае для любого x E1 выполняется усло-
вие |
lim n |
| an xn | L | x | 0 1, и потому степенной ряд сходится при всех |
||||
|
n |
|
|
|
|
|
x , причём абсолютно, |
так что R . Если же |
L , то для любого |
x 0 |
|||
выполняется условие |
|
|
|
|
||
|
|
lim n | an xn | lim n | an || x |n |
lim |
n | an | | x | , |
|
|
|
|
n |
n |
n |
|
|
и потому ряд расходится при любом x 0 . Отсюда следует, что R 0.
Таким образом, радиус сходимости степенного ряда может быть найден по формуле
R |
1 |
|
1 |
, |
|
L |
lim n | an | |
||||
|
|
|
|||
|
|
|
n |
|
34

в предположении, что предел lim n | an | существует. При этом если он равен
n
0 (L 0) , то полагают |
R . Если же |
lim n | an | |
(L ), то полагают |
|
|
n |
|
R 0.
Ещё раз отметим, что если R 0, то ряд будет сходиться только при x 0 , если же R , то ряд сходится при всех действительных x , причём абсо-
лютно.
П р и м е р ы
|
|
|
|
|
|
|
|
|
|
|
|
|
1. 1 2x 3x2 ... (n 1)xn |
... |
(n 1)xn . |
|
|||||||||
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
В данном случае an n 1 , n 0,1, 2,... . Поэтому |
|
|||||||||||
|
|
|
|
R lim |
|
an |
|
lim |
|
n 1 |
1. |
|
|
|
|
|
|
|
|
||||||
|
an 1 |
|
|
|||||||||
|
|
|
|
n |
|
n |
|
n 2 |
|
|||
Значит, ряд сходится, причём абсолютно, |
для всех x , удовлетворяющих не- |
|||||||||||
равенству |
|
x |
|
1, т.е. для всех x |
|
из интервала ( 1;1) . При |
x 1 и x 1 ряд |
|||||
|
|
|
||||||||||
расходится (общий член получающихся рядов не стремится к нулю при n ). Таким образом, областью сходимости данного ряда является интер-
вал ( 1;1) , радиус сходимости R 1.
2. n!xn .
n 0
Определим радиус сходимости данного ряда:
R lim |
|
an |
|
lim |
n! |
|
lim |
1 |
|
0 . |
an 1 |
n 1 ! |
|
|
|||||||
n |
|
|
n |
n n 1 |
|
|||||
Поэтому ряд сходится только при x 0.
3. xn
n 0 n!
Вычислим радиус сходимости этого ряда:
|
an |
|
|
n 1 ! |
lim n 1 . |
||
R lim |
|
|
lim |
||||
an 1 |
n! |
||||||
n |
|
|
n |
n |
|||
Получили, что ряд сходится на всей числовой прямой, т.е. при | x | .
35

|
|
x |
n |
|
|
|
|
|
|
|
|
|
|
|
4. 1 n 1 |
|
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
n 1 |
|
n |
|
|
|
|
|
|
|
|
|
|
||
Вычислим радиус сходимости данного ряда: |
|
|
||||||||||||
|
|
|
|
|
|
an |
|
|
|
lim n 1 |
|
|
||
|
|
|
|
R lim |
|
|
|
1. |
|
|||||
|
|
|
|
|
an 1 |
|
|
|||||||
|
|
|
|
n |
|
|
|
|
|
n |
n |
|
|
|
Отсюда |
видно, что интервалом |
|
|
|
сходимости ряда |
является интервал |
||||||||
( 1;1). Проверим сходимость ряда в точках |
x 1. При |
x 1 имеем сходя- |
||||||||||||
щийся по признаку Лейбница ряд |
1 |
1 1 .... |
|
|
||||||||||
|
|
|
|
1 |
|
|
||||||||
|
|
|
|
|
2 |
3 |
4 |
|
|
|
||||
При x 1 имеем расходящийся ряд |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 1 1 |
1 ..., |
|
|
|||||||
|
|
|
|
|
2 |
3 |
4 |
|
|
|
||||
являющийся с точностью до знака гармоническим рядом. Таким образом, об-
ластью сходимости данного ряда является промежуток 1;1 , т.е. все |
x , |
|||||||||||||||||||||||||||||||||||||||||
удовлетворяющие неравенству 1 x 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
5. |
|
n 1 |
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
2n 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
В данном случае an |
|
|
|
n 1 |
|
|
|
|
|
|
L lim n | an |
| |
lim |
|
|
|
n 1 |
1 n |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
, |
и потому |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
5 |
|
|
2n 5 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
n 1 |
|
n 1 |
n |
|
|
|
|
|
|
n |
1 |
|
|
|
|
n 1 |
n |
|
1 |
|
|
1 |
|
1 |
|
|
|
|||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
. |
|
||||
2n 5 |
2n 5 |
2n 5 |
|
|
|
2 |
|
2 |
2 |
|
||||||||||||||||||||||||||||||||
n |
|
|
|
|
n |
|
n |
2n 5 |
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
Получаем, что R |
|
1 |
|
2 и что интервал сходимости рассматриваемого ряда |
||||||||||||||||||||||||||||||||||||||
|
L |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 . |
|
|
|
|
|
|
|
|
|
|||||
имеет вид ( 2;2). Исследуем сходимость ряда в точках |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
При |
|
x 2 получаем числовой ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
n 1 |
n 2 |
n |
|
|
|
|
|
n |
1 |
n |
|
n n 1 |
2 |
|
|
2n 2 |
n |
n 1 |
|
|
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||||
2n 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
n 0 |
|
|
|
|
|
|
|
n 0 |
|
|
2n 5 |
|
|
|
|
|
2n 5 |
|
n 0 |
|
2n 5 |
|
2n 5 |
|
|
|||||||||||||||||
36
Покажем, что для такого ряда не выполняется необходимое условие сходимости: его общий член не стремится к 0 при n . Действительно, посколь-
ку
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 5 |
|
|
3n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
3 |
n |
|
|
|
3 |
|
|
2n 5 |
|
|
|
3 |
|
||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||||
|
2n 2 |
2n 5 3 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
e |
|
2 , n , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2n 5 |
|
2n 5 |
|
|
|
|
2n 5 |
|
|
|
|
2n |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
2 |
|
1 2 |
|
1 |
|
n , то |
|
|
|
2n 2 |
n |
n 1 |
2 |
|
1 |
e |
|
3 |
0. |
|||||||||
|
|
|
|
|
|
|
|
|
, |
lim |
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||
|
2n 5 |
4 |
2n 5 |
2n 5 |
4 |
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||||||||
Поэтому этот числовой ряд расходится, что означает расходимость степенного ряда в точке x 2.
При x 2 получаем знакочередующийся числовой ряд, абсолютная ве-
личина n -го члена которого равна |
|
2n 2 |
n |
n 1 |
2 |
|||
|
|
|
|
. Необходимое усло- |
||||
2n 5 |
2n 5 |
|||||||
|
|
|
|
|
|
|||
вие сходимости для такого числового ряда не выполняется, и потому он расходится. Таким образом, данный степенной ряд расходится и в точке x 2 . Поэтому областью сходимости заданного степенного ряда является
его интервал сходимости.
|
|
|
|
|
|
|
|
|
|
|
|
n 3n |
3x 1 n |
|||||
6. Найти область сходимости функционального ряда |
|
|
|
|
|
|
. |
|||||||||||
4 |
n |
5 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
||||
Заменой z |
3x 1 |
данный функциональный ряд преобразуется в степен- |
||||||||||||||||
2 |
||||||||||||||||||
ной ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
n 3 |
zn . |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
n 1 4 |
5 |
|
|
|
|
|
|
|
|
|||
Найдём интервал сходимости такого степенного ряда. Поскольку |
|
|
|
|||||||||||||||
|
|
an |
n 3n , an 1 n 1 3n 1 , |
|
|
|
|
|
|
|
||||||||
|
|
|
|
4n |
5 |
|
4n 1 5 |
|
|
|
|
|
|
|
||||
|
|
an |
|
lim |
n 3n |
4n 1 5 |
|
|
|
|
|
|
|
|||||
|
то lim |
|
|
|
|
|
|
|
|
|||||||||
|
an 1 |
n 1 3n 1 |
|
|
|
|
|
|
||||||||||
|
n |
|
n |
4n 5 |
|
|
|
|
|
|
|
|||||||
37
|
n 3n |
|
4n 1 |
5 |
|
|
|
|
|
|
n 3n |
|
|
4n 1 5 |
|
|
|
n |
1 |
|
||||||||
lim |
|
lim |
|
|
lim |
lim |
|
|
3n |
|
||||||||||||||||||
n 1 3n 1 |
4n |
5 |
|
|
|
|
|
|
|
3n 1 |
4n 5 |
|
|
|
1 |
|
|
|||||||||||
n |
|
|
n |
n 1 |
|
n |
n n |
3 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
5 |
|
|
1 |
|
|
4 . |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
lim |
|
|
4n |
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
n |
1 |
|
5 |
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
4n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, R 43 и интервал сходимости имеет вид ( 43 ; 43). Выясним поведение ряда в точках z 43 . При z 43 получаем числовой ряд
|
|
n |
|
n |
nn 3 |
|
4n , |
||
n 1 |
4 |
5 |
|
3 |
который является расходящимся, поскольку его общий член не стремится к нулю при n .Действительно,
lim |
n 3n 4n |
lim |
4n |
n 3n |
lim |
4n |
lim |
n 3n |
lim |
|
|
1 |
|
|
|
|
4n 5 |
3n |
|
|
|
5 |
|
||||||||
n |
4n 5 3n |
n 4n 5 |
3n |
n |
n |
n |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4n |
|
|
|||
|
|
|
lim ( |
n |
1) |
1 1 1 0. |
||
|
|
|
3n |
|||||
|
|
|
n |
|
|
|
|
|
При |
z |
4 |
получаем знакочередующийся числовой ряд |
|||||
|
|
3 |
|
|
|
|
n |
n |
|
|
|
|
|
|
|||
|
|
|
( 1)n nn 3 |
4n , |
||||
|
|
|
|
n 1 |
4 |
5 |
3 |
|
общий член которого также не стремится к нулю при n , и потому этот ряд тоже расходится. Таким образом, множеством сходимости степенного
ряда является интервал ( 43 ; 43). Найдём теперь область сходимости исходного ряда. Она представляет собой множество всех решений неравенства
|
4 |
|
3x 1 |
|
4 . |
|
3 |
|
2 |
|
3 |
38
Решив это неравенство, получим: множеством сходимости исходного ряда является интервал ( 95 ;119 ).
2.2.2. Разложение функций в степенные ряды
Рассмотрим степенной ряд
|
a |
|
a x a |
x2 ... |
a |
xn ... |
(2.9) |
||
|
0 |
|
1 |
2 |
|
n |
|
|
|
с радиусом сходимости R 0 (возможно, |
R ). При каждом x |
из интер- |
|||||||
вала сходимости R ; R |
ряд сходится, так что его сумма является функцией |
||||||||
от x . Обозначив эту сумму через |
f x , можно записать: |
|
|||||||
f x a |
a x a |
x2 |
... a xn ..., x R ; R . |
(2.10) |
|||||
0 |
1 |
|
2 |
|
|
n |
|
|
|
Определение. Если функция |
f x является суммой степенного ряда (2.9) |
||||||||
на интервале R ; R , то говорят, что функция |
f x разлагается на этом ин- |
тервале в степенной ряд. |
|
В ряде случаев будем рассматривать также степенные ряды более общего вида:
a |
a |
x x |
a |
x x |
2 |
... a |
x x |
n ... . |
(2.11) |
0 |
1 |
0 |
2 |
0 |
|
n |
0 |
|
|
Ряд (2.9) является частным случаем ряда (2.11) при x0 0 . Ряд (2.11) сводится к ряду (2.9) с помощью замены t x x0 . Поэтому интервал сходимо-
сти ряда (2.11) будет определяться неравенством |
|
t |
|
R , или |
|
x x0 |
|
R , где |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
R радиус сходимости |
степенного ряда antn , |
0 R , и потому будет |
|||||||
|
n 0 |
|
|
|
|
|
|
|
|
иметь вид |
x0 R x x0 R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В случае R 0 ряд |
(2.11) будет сходиться только в точке x x0 , а при |
||||||||
R он будет сходиться при всех x. |
|
|
|
|
|
|
|
|
|
Отметим, что интервалом сходимости ряда (2.11) является интервал, симметричный относительно точки x x0 (рис. 3).
39

Рис. 3. Интервал сходимости степенного ряда (2.11) в случае 0 R
Определение. Если функция f x является суммой |
степенного ряда |
(2.11) на интервале x0 R; x0 R , то говорят, что функция |
f x разлагается |
на этом интервале в степенной ряд по степеням x x0 . |
|
Поскольку ряд (2.11) заменой переменной может быть сведён к ряду (2.9), то всё изложенное ранее и то, что будет излагаться далее для рядов вида (2.9), будет справедливо и для рядов вида (2.11).
Приведём основные свойства сумм степенных рядов.
1. Если функция f (x) на интервале R ; R разлагается в степенной ряд
(2.9) так, что справедливо равенство (2.10), то на этом интервале функция f (x) дифференцируема и её производная f x может быть найдена в каж-
дой точке интервала сходимости почленным дифференцированием степенного ряда:
f x a1 2a2 x ... nan xn 1 ... .
З а м е ч а н и е. Аналогично могут быть найдены производные любого порядка m 1 функции f (x) , при этом соответствующие ряды (полученные
почленным дифференцированием ряда (2.9) m раз) будут иметь тот же ин-
тервал сходимости, что и исходный ряд.
2. Если функция f x на интервале R ; R разлагается в степенной ряд (2.9), то на любом отрезке, содержащемся в этом интервале, функция f x
интегрируема и интеграл от неё может быть найден почленным интегрированием степенного ряда.
|
Другими |
словами, если |
x1 и |
x2 |
произвольные |
точки из |
интервала |
|||||
R ; R , то |
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
x |
|
x |
|
x |
|
|
2 |
f x dx 2 |
a0 |
a1 x a2 x2 ...+ an xn ... dx 2 |
a0dx 2 |
a1 xdx ... 2 |
an xndx ... |
||||||
x1 |
x1 |
|
|
|
|
x1 |
|
x1 |
|
x1 |
|
|
|
a0 x2 |
x1 |
a1 x22 x12 |
a2 |
x23 |
x13 ... |
|
an |
|
|
x2n 1 x1n 1 .... |
|
|
n 1 |
|
||||||||||
|
|
|
2 |
3 |
|
|
|
|
|
|
||
40
