
2813.Планетарные передачи в автомобилестроении
..pdf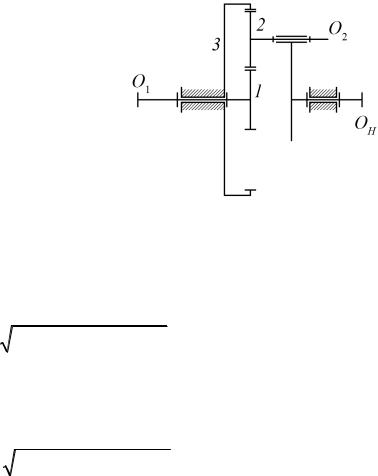
Для получения однозначного решения вводятся следующие ограничения:
1)зубчатые колеса 1 и 2, а также колеса 2 и 3 (см. рис. 2.20) должны образовать неисправленное (нормальное) зацепление;
2)угол зацепления в сборке αсб = 20°
ивысота головок зубьев hг= m;
3)при зацеплении зубчатых колес не должно быть их заклинивания, причем условие отсутствия заклинивания заключается в том, что
а) для внешнего зацепления число зубьев на меньшем колесе не должно быть меньше, чем
Рис. 2.20. Схема одноступенчатого планетарного редуктора Джеймса
z = 2 |
i2 |
+ (2i + 1)sin |
2 α |
сб |
+ i |
|
||
12 |
12 |
|
|
12 |
; |
(2.38) |
||
|
|
|
|
|
|
|||
1min |
(2i + 1)sin2 |
α |
|
|
|
|
|
|
|
|
сб |
|
|
|
|||
|
|
12 |
|
|
|
|
||
б) для внутреннего зацепления число зубьев на меньшем колесе не должно быть меньше, чем
z2min = 2 |
i2 |
− (2i |
− 1)sin |
2 α |
сб |
+ i |
|
|
23 |
12 |
|
|
|
23 |
(2.39) |
||
|
(2i |
− 1)sin2 α |
сб |
|
||||
|
|
23 |
|
|
|
|
||
(в этих формулах передаточное отношение i12 и i23 берется по своему абсолютному значению и предполагается равным единице или больше);
4) габариты механизма должны быть наименьшими.
При проектировании редукторов указанного типа необходимо соблюдать следующие условия:
а) условие соосности
z3 = z1 + 2z2, |
(2.40) |
||||
б) условие соседства |
|
|
|
|
|
sin |
180 |
≥ |
z2 + 2 |
, |
(2.41) |
|
|
||||
|
k |
|
z1 + z2 |
|
|
где k – число сателлитов, |
|
|
|
|
|
в) условие сборки: |
|
|
|
|
|
kmax = z1 + z3, |
(2.42) |
||||
где k – максимально возможное число сателлитов, располагающихся в параллельных плоскостях; фактическое число сателлитов будет равно
71

k = kmax/ E, |
(2.43) |
где E – одно из множителей числа kmax; число сателлитов k, получаемое из настоящего условия, не должно превышать их число, найденное из условия соседства.
Пример
Спроектировать одноступенчатый однорядный редуктор типа Джеймса, если заданы передаточное отношение i1(3)H = 4 и модуль m = 2 мм
(см. рис. 2.20). Требуется найти числа зубьев всех колес, наибольшее число сателлитов и радиусы начальных (делительных) окружностей для всех зубчатых колес.
Решение
1. Определяем передаточное отношение i13( H ) от колеса 1 к колесу 3 при остановленном водиле Н.
Из условия, что i1(3)H = 1 – i13( H ) , получаем
i13( H ) = 1− i1(3)H = 1− 4 = −3 = 3 .
2. Определяем передаточное отношение i12( H ) от колеса 1 к колесу 2 при остановленном водиле Н.
Из условия соосности (2.40) имеем, что z1 + 2z2 = z3, так как i13( H ) = z3 / z1,
то z3 |
= z1·i( H ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя значение z3 в формулу (2.40), получаем z1+2z2 |
= z1·i( H ) , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( H ) |
= |
z |
2 |
= |
|
i( H ) − 1 |
= |
|
3 |
− 1 |
= 1. |
|
|||||||||||
|
|
i |
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
12 |
|
|
|
|
z1 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3. Определяем передаточное отношение i( H ) |
от колеса 2 к колесу 3 при |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
остановленном водиле Н. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
В формулу (2.40) подставляем значение z1, выраженное через i( H ) . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
Получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
+ 2z2 |
= z3 , |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
i( H ) |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 2 1 |
|
|
|||||||
|
|
( H ) |
= |
|
z |
3 |
|
= |
1 |
+ 2i( H ) |
= |
= 3. |
|
|||||||||||||
|
i |
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
23 |
|
|
|
z |
|
|
|
|
|
|
|
i( H ) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
72
4. Находим наименьшие допустимые числа зубьев на колесах 1 и 2: а) на колесе 1 по формуле (2.38):
|
= 2 |
i2 |
+ (2i |
|
+ 1)sin2 α |
сб |
+ i |
= 2 |
|
12 + (2 1+ 1)0,117 |
+ 1 |
= 12,5, |
||||||||
z |
12 |
12 |
|
|
|
|
12 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(2 1+ 1)0,117 |
|
|||||||
1min |
|
|
|
(2i |
+ 1)sin2 |
α |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
сб |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
т.е. должно быть z1 ≥ 13; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) на колесе 2 по формуле (2.39): |
|
|
|
|
|
|
|
|||||||||||||
|
= 2 |
|
i2 |
− (2i |
|
− 1) sin |
2 α |
сб |
+ i |
= 2 |
|
32 − (2 3 − 1)0,117 + 3 |
= 20,2 |
|||||||
z2min |
|
23 |
12 |
|
|
|
|
|
|
23 |
|
|
|
|
|
|||||
|
|
(2i |
− 1) sin2 |
α |
сб |
|
|
|
(2 3 − 1)0,117 |
|
|
|
||||||||
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. должно быть z2 ≥ 21.
5. Производим подбор чисел зубьев на колесах 1, 2 и 3 при условии,
что i12 = 1, z1 ≥ 13 и i23 = 3, z2 ≥ 21. Если принять, что z1 = 14, то получится z2 = 14, но 14 < 21. Поэтому принимаем, что z1 = 22. Тогда z2 = 22, и так как
22 > 21, то число z1 = 22 оказалось приемлемым, следовательно, будем иметь z3 = 66.
Переходим далее к подбору максимального числа сателлитов. 6. Из условия соседства (2.41) имеем, что
sin |
180 |
≥ |
z2 |
+ 2 |
= |
22 |
+ 2 |
= |
24 |
= 0,545, |
|
|
k |
z1 + z2 |
22 + 22 |
44 |
|||||||
|
|
|
|
|
|
||||||
откуда 180°/k = 33°, или число сателлитов k < 180/33 = 5,45. Таким образом, можно поставить не более 5 сателлитов. 7. Из условия сборки (2.43) имеем
k = z1 + z3 = 22 + 66 = 88 ,
E E E
гдеЕ– целое числоиодно изсомножителейчиселkmax = z1+z3 (формула (2.42)). Очевидно, чтобы получить k ≤ 5, надо положить Е = 22, и тогда число
сателлитов будет равно 4. Окончательно принимаем k = 4.
Далее определяем радиусы начальных (делительных) окружностей всех колес (мм):
для колеса 1: R = |
mz1 |
= |
2 22 |
= 22, |
|||||||
|
|
|
|
|
|
||||||
1 |
2 |
2 |
|
|
|
||||||
|
|
|
|
||||||||
для колеса 2: R = |
mz2 |
|
= |
|
2 22 |
= 22, |
|||||
|
|
|
|
||||||||
2 |
2 |
2 |
|
|
|
||||||
|
|
|
|
||||||||
для колеса 3: R = |
mz3 |
|
= |
2 66 |
= 66. |
||||||
|
|
|
|||||||||
3 |
2 |
2 |
|
|
|
||||||
|
|
|
|
||||||||
73
3.СТРУКТУРА ПЛАНЕТАРНЫХ МЕХАНИЗМОВ
3.1.Структурная формула планетарных механизмов
Рассматриваемые планетарные зубчатые механизмы обладают следующими свойствами:
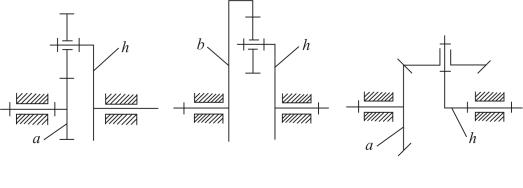
а) каждый состоит из некоторого числа простейших планетарных механизмов (рис. 3.1), которые не могут быть расчленены на более элементарные самостоятельные механизмы;
б) водило (звено H) любого простейшего механизма, входящего в состав исследуемых механизмов, либо имеет подвижную в пространстве ось вращения, либо неподвижно (в последнем случае имеем простейшую зубчатую передачу);
в) угловые скорости трех основных звеньев а, b и h связаны зависимостью
ih = (ωa − ωh ) / (ωb − ωh ).
Звенья, обладающие неподвижной в пространстве осью вращения, назовем основными звеньями.
Рис. 3.1. Примеры простейших планетарных механизмов
Число степеней свободы в планетарных механизмах может быть подсчитано по структурной формуле плоского механизма, называемой формулой Чебышева:
W = 3n – 2p5 – p4,
где n – число подвижных звеньев; 2p5 – число низших кинематических пар; p4 – число высших кинематических пар.
Если принять p5 = n, то получим
W = n – p4 .
74
В планетарных механизмах n = n0 + kм , где k – число сателлитов, от которого зависит определенность движения, k = kм ; n0 – число основных
звеньев. Число высших пар равно числу pz зацеплений, активно влияющих на число степеней свободы, т.е. p4 = pz = 2kм . Учитывая принятые значения,
получим:
W = n0 − kм.
Структурная формула показывает, что при расчете сложного планетарного механизма можно иметь в виду только основные звенья и составляющие механизмы, поэтому кинематическая схема может быть заменена структурной. На рис. 3.4 показана структурная схема, соответствующая кинематической, приведенной на рис. 3.2. Очевидно, структурная схема раскрывает связи между планетарными механизмами и показывает принципиальную возможность построения на ее основе множества кинематических схем, осуществляющих заданные передаточные отношения.
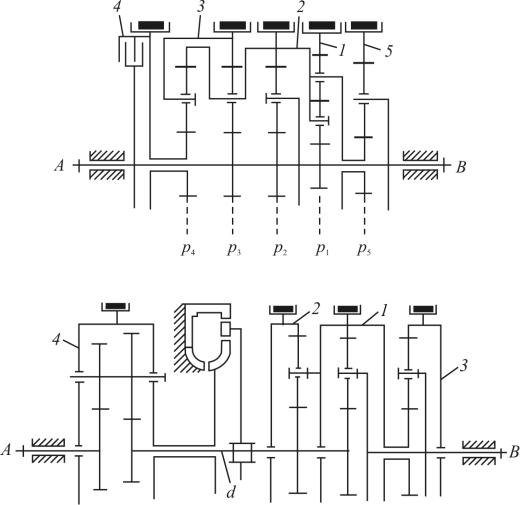
Рис. 3.2. Планетарная коробка передач: 1–5 планетарные ряды
Рис. 3.3. Гидромеханическая коробка передач: 1–4 планетарные ряды
75

Рис. 3.4. Структурная схема планетарной коробки: 1–5 планетарные ряды
Число σ кинематических схем, получаемых из одной такой структурной схемы, определяется как число размещений с повторениями из числа π кинематических схем в одном составляющем механизме по числу kм таких
механизмов в структурной схеме, т.е.
σ (π, kм ) = πkм .
Рис. 3.5. Структурная цепь (а), структурная (б) и кинематические (в) схемы простого планетарного механизма
Если в сложном механизме находятся механизмы различного вида (см. рис. 3.3), то имеем следующую зависимость:
σ = ∏S (πkм )j,
j = 1
где j – число видов механизмов, j = 1, 2, …, S.
Для простых планетарных механизмов имеем n0 = 3 kм = 1 и на основа-
нии структурной формулы W = 2. Назовем структурной цепью простого планетарного механизма его условное изображение в виде прямоугольника (рис. 3.5, а), где основные звенья показаны прямыми линиями.
76
Структурной схемой простой передачи (рис. 3.5, б) называется структурная цепь, в которой основным звеньям δ1, δ2 , δ3 присвоены индексы ве-
дущего А, ведомого В и опорного звена d без указания, какие из этих звеньев будут центральными колесами и какие водилами. Если в структурной схеме (рис. 3.5, б) обозначения звеньев заменить обозначениями цетральных колес и водила, то получим 3п = 6 различных кинематических схем, одна из которых показана на рис. 3.5, в.
3.2. Структура сложных планетарных механизмов
Чтобы найти наиболее простую схему сложного планетарного механизма, например коробки передач, необходимо иметь способы определения наименьшего числа ее звеньев, планетарных механизмов и элементов управления.
Рассматриваемые коробки передач в общем случае могут иметь W = 2, 3, …, поэтому в однодвигательном варианте для получения передачи с одной степенью свободы нужно устранить W – 1 степеней свободы. С этой целью коробки передач снабжаются элементами управления – тормозами и муфтами. Следовательно, общее число элементов управления
m = T + Ф,
где Т – число тормозов; Ф – число фрикционных муфт. Включение каждого элемента управления приводит к жесткому соединению двух звеньев между собой. Соединение двух звеньев уменьшает число n0 на единицу и снижает
на столько же в число степеней свободы коробки передач, что следует из формулы. Поэтому если последняя обладает W степенями свободы, то одновременно включение W – 1 таких элементов превратит коробку в механизм с одной степенью свободы. Чтобы получить несколько скоростей, коробка передач должна содержать
m > W − 1.
В этом случае элементы управления могут быть включены в различных комбинациях в число n передач, осуществляемых коробкой, они определяются как число сочетаний из m элементов управления по числу элементов, включаемых одновременно для получения передач, т.е.
n = CmW −1 .
Знак неравенства отмечает случай, когда используются не все возможные комбинации включения (W – 1) элементов управления.
77
Сравним коробки по числу потребных для заданного числа передач элементов управления: для коробок передач с двумя степенями свободы
n = Cm1 = m.
Для коробок передач с числом степеней свободы больше двух при m = W имеем также
n = Cmm−1 = Cm1 = m.
Итак, в случае m = W все типы коробок передач равноправны как обладающие числом элементов управления, равным числу передач. Однако необходимость одновременного включения большего числа элементов управления усложняет процесс управления планетарной коробки передач, имеющей большее число степеней свободы. Поэтому коробки передач с числом степеней свободы больше двух выгоднее применять при m >W.
В общем случае m ≥W.
Стремление к упрощению схемы за счет уменьшения m приводит к созданию устройств, в которых используются все возможные комбинации включений числа (W – 1) элементов управления.
Наибольшее число муфт, устанавливаемых в подобных коробках, должно быть не больше числа одновременно включаемых для получения передачи элементов управления
Ф≤ W − 1.
Число фрикционных муфт, подсчитанное при знаке равенства, является достаточным для получения прямой передачи. Возможное упрощение конструкции может быть достигнуто увеличением числа Ф. Общее число основных звеньев коробки
n0 = t + l + 2,
где t – число тормозных звеньев, равное числу тормозов Т; l – число вспомогательных звеньев; 2 – число ведущих и ведомых звеньев.
Подставив значения n0 из структурной формулы, получим kм = t + l + W + 2,
отсюда уменьшение числа kм планетарных механизмов и, следовательно,
возможное упрощение конструкции при прочих равных условиях достигается уменьшением t или увеличением Ф. В случае проектирования коробок с полным использованием элементов управления должно выполняться ус-
78
ловие Ф≤ W − 1, в противном случае будет иметь место совпадение передач. Этим лишний раз подтверждается необходимость использования прямой передачи.
Упрощение конструкции коробки передач за счет уменьшения числа механизмов, содержащихся в ней, приводит к созданию схем, использующих сравнительно большее число элементов управления. В подобных конструкциях элементы управления используются неполностью. Именно такие коробки передач находят широкое применение в машиностроительной практике.
В коробках передач с неполным использованием элементов управления все основные звенья, за исключением ведущего и ведомого, могут быть тормозными, т.е.
t ≤ n0 − 2.
Это выражение может быть получено также подстановкой в
n0 = t + l + 2
значения l ≥ 0. Поскольку каждая муфта соединят два звена, то теоретиче-
ски в схеме коробки их можно разместить C2 . Назовем равноценными та-
n0
кие размещения, которые являются вариантами блокировки двух любых звеньев из трех основных q, r и s, входящих в планетарный механизм, как
приводящие к одному и тому же, поэтому их общее число будет |
Cn0 − 2kм. |
|
2 |
Установку муфты между ведущими и ведомыми звеньями следует признать нецелесообразной.
При включении одной муфты U, блокирующей ведущее и ведомое звенья, устанавливается передача в коробке. Поэтому включение любых W – 1 элементов управления, среди которых есть элемент U, будет приводить к одному и тому же передаточному числу, и в результате из CmW −1 возможных
передач выпадает CmW−−12. На основании комбинаторного тождества имеем
CmW −1 − CmW−−12 = CmW−−11,
т.е. подобная коробка передач будет воспроизводить число n ≤ CmW−−11 переда-
точных чисел, которое можно обеспечить применением коробок, содержащих на один элемент управления меньше. Следовательно, число различных размещений одной муфты в схеме коробки передач с неполным использованием элементов управления или число муфт, допустимое к установке, составит
79
Ф≤ C2 − 2kм − 1.
n0
Знак неравенства соответствует случаю, когда установка числа Ф муфт невозможна без пересечения звеньев.
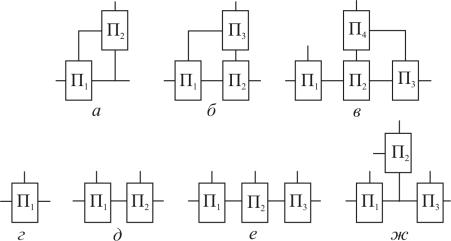
Найдем число планетарных механизмов, необходимое и достаточное для образования коробки передач с W степенями свободы, т.е. найдем такое их число, уменьшение которого хотя бы на единицу приводит или к нарушению связности схемы, или к изменению числа степеней свободы. Для этого необходимо, чтобы в коробке передач отсутствовали механизмы с тремя основными звеньями, обладающие нулевой степенью подвижности относительно тех звеньев, которыми они соединяются с другими. Такими механизмами являются, например, механизмы П2, П3, П4 (рис. 3.6, а, б, в), в чем нетрудно убедиться, рассматривая степень подвижности отмеченных механизмов относительно двух любых соосных звеньев, жестко сблокированных между собой. Следовательно, отсоединение механизмов П2, П3, П4 от любой структурной цепи не изменяет числа степеней свободы.
Исключение же из структурных цепей (см. рис. 3.6, г–ж) любого механизма приведет к изменению числа степеней свободы или к нарушению связности. Заметим, что начиная со структурных цепей, состоящих из трех механизмов с тремя основными звеньями, могут получаться боковые ответвления (см. рис. 3.6, ж) подобных механизмов. Из приведенных примеров следует, что механизмы с нулевой степенью подвижности будут отсутствовать в такой структурной цепи, в которой каждый из них соединяется с другими только одним основным звеном. Для этого необходимо и достаточно, чтобы число соединений основных звеньев между собой, равное числу Wy устраняемых степеней свободы, было равно числу механизмов без единицы, т.е. равно kм − 1. Число устраняемых степеней свободы Wy = 2kм − 1.
Рис. 3.6. Структурные цепи механизмов: а–ж – планетарные ряды
80
