1465

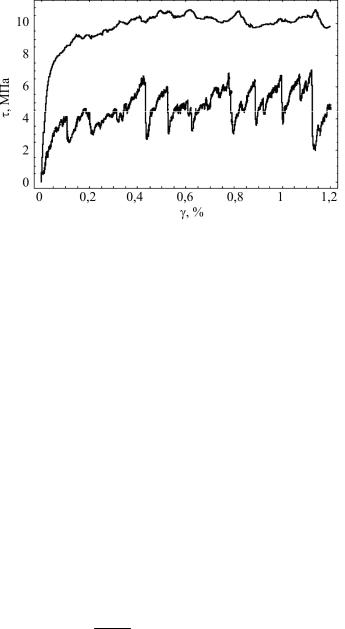
и перестройки дислокационной структуры сопровождаются локальными падениями напряжений (временная нестабильность), появляющимися при небольших скоростях деформирования (рис. 3.17). Эти падения наблюдаются и в достаточно тонких натурных экспериментах и известны под названием эффекта Портвена-Ле Шателье.

Рис. 3.17. Диаграммы деформирования с относительно высокой (верхняя кривая) и низкой (нижняя кривая)

скоростей деформирования

Рассмотрим пример модификации модели движения дислокаций одной системы скольжения для учета диффузии примеси. При моделировании диффузии примесных атомов используются правила для диффузии, сформулированные с помощью окрестности Марголуса. Для учета взаимодействия атомов с дислокациями в потоковый член уравнения баланса концентрации этих атомов необходимо включить дополнительное слагаемое – градиент потенциала взаимодействия атомов и дислокации. В данном подходе предлагается численная реализация аддитивности потоков диффузии атомов, вызванных градиентом концентрации и градиентом потенциала взаимодействия с дислокациями, с помощью последовательности итераций работы имитатора. Сила, действующая на примесный атом со стороны дислокации, находится как

где х и у – координаты примесного атома в системе координат, связан-

ной с дислокацией; χ ≡ r1 − r0 – относительное несовпадения радиусов r1

191

r0 – внедряемого в материал атома, и r1 – атома материала или вакансии (в зависимости от механизма диффузии); W – потенциал взаимодействия примесного атома и дислокации в изотропной линейно-упругой среде,

ми результирующая сила находится как суперпозиция сил, действующих на атом со стороны всех дислокаций:

где M + – число положительных краевых дислокаций, а M – – число отрицательных краевых дислокаций. Принимается, что движению примесных атомов препятствует пороговая сила, которая связана с энергией активации миграции примесных атомов. Если найденная сила F0 превышает по модулю значение пороговой силы, то атом переходит в соседнюю клетку в направлении, соответствующем силе F0.

Вопрос учета в клеточных автоматах реального физического времени является открытым, единой методики его решения не существует. В построенной модели удается учесть физическое время, используя экспериментальный факт о линейной зависимости скорости движения дислокации от действующей на эту дислокацию силы при не слишком больших скоростях движения дислокаций. Зная силы, действующие на каждую дислокацию, можно определить их скорости. Согласно правилам клеточного автомата за одну итерацию каждая дислокация смещается не более чем на одну клетку, поэтому, принимая, что «самая быстрая» дислокация должна переместиться не дальше чем на одну клетку, можно определить длительность текущей итерации. Дислокации, которые за это время не успевают покинуть свою клетку, не перемещаются. Таким образом, разные итерации длятся различное физическое время. Отметим, что физическое время перемещения дислокации на расстояние, равное размеру клетки, очень мало. Поэтому исследование медленного нагружения требует рассмотрения очень большого числа итераций и размеров области моделирования. Результаты, получаемые за разумное вычислительное время, соответствуют очень быстрому изменению приложенных воздействий. Совместное движение дислокаций и примесных атомов реализуется как последовательный пересчет их конфигураций. На каждом новом шаге в качестве начальных условий используются конфигурации дислокаций и примесных атомов, полученные на предыдущем шаге. Учет фи-

192

зического времени позволяет исследовать процессы нагружения при любой скорости. Конфигурации дислокаций и примесных атомов, приведенные на рис. 3.18, получены при «быстром» нагружении.

а

б

в

Рис. 3.18. Конфигурации дислокаций и примесных атомов: а – начальное случайное распределение дислокаций; б – формирование первых дислокационных субструктур, миграция к ним атомов; в – сформировавшиеся дислокационные субструктуры и атмосферы

193

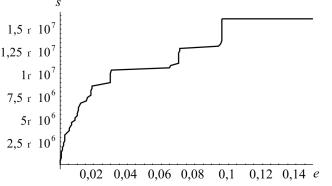
В начале нагружения дислокации образуют диполи, по мере роста напряжений начинают образовываться дислокационные стенки. При этом атомы примеси диффундируют к отдельным дислокациям и простейшим субструктурам, образуя вокруг них скопления в виде облаков. Система приходит в устойчивую конфигурацию, дислокации совершают лишь незначительные колебания, так что суммарное приращение деформации остается нулевым или меняется крайне незначительно. Концентрация примесных атомов в это время становится все более неоднородной – повышается их концентрация в местах скопления дислокаций. Время нахождения системы в этой конфигурации соответствует вертикальному (или почти вертикальному) участку кривой на диаграмме σ–ε (рис. 3.19). Далее с ростом внешнего приложенного напряжения одна или несколько дислокаций начинают скольжение, что соответствует горизонтальному участку кривой деформирования (см. рис. 3.19), при этом происходит и перемещение дислокационных диполей вследствие возникающих градиентов напряжений. В первую очередь скользить начинают одиночные дислокации и диполи, еще не закрепленные облаками примесных атомов. Затем конфигурация вновь становится равновесной, и дислокации останавливаются. Таким образом, на макродиаграмме «напряжение-деформация» образуются ступеньки. При достижении достаточного напряжения движение начинают дислокационные стенки, сдвиговые деформации при этом получаются значительно бó льшими по сравнению со скольжением единичных дислокаций – это соответствует широким ступенькам на диаграмме. При дальнейшем росте приложенного сдвигового напряжения атомы не успевают закреплять дислокационные субструктуры и последние движутся, реализуя значительные пластические деформации.

Рис. 3.19. Соответствующая диаграмма деформирования, σ (Па) – величина сдвигового напряжения

194

С помощью разработанной модели можно исследовать довольно тонкие процессы, идущие во внутренних областях тел, подвергаемых интенсивному пластическому деформированию. В частности, модель позволяет исследовать динамику изменения дислокационной структуры в поле диффундирующих примесных атомов при быстром нагружении, процесс формирования ячеистой дислокационной микроструктуры при сложном нагружении частиц порошка в процессе механического легирования. Описанная модель позволяет проводить численные эксперименты для проверки физических механизмов, закладываемых в макрофеноменологические модели пластического деформирования и диффузии в материале с изменяющейся дислокационной структурой.

Рассмотренные дискретные модели представляют собой инструмент теоретического исследования процессов на уровне представительного объема материала. Исследовать с их помощью поведение тел макроскопического масштаба не представляется возможным. Но сами эти модели являются некоторым оператором, заменяющим определяющие соотношения на микроскопическом масштабном уровне.

Вопросы для самопроверки

1.Что такое периодические граничные условия?

2.Каким образом реализуется случайное блуждание частицы в клеточном автомате с правилами Марголуса?

3.Что такое «мягкое» и «жесткое» нагружение?

4.Как определяется приращение тензора пластических деформаций, если известно приращение сдвигов по различным системам скольжения?

5.Каков механизм формирования атмосфер примесных атомов вблизи дислокационных субструктур?

6.Как влияют атмосферы примесных атомов на подвижность дислокаций?

7.Объяснить механизм движения диполей краевых дислокаций за счет градиентов напряжений.

Список литературы к главе 3

1.Бусленко В.Н. Автоматизация имитационного моделирования сложных систем. – М.: Наука, 1977. – 240 с.

2.Введение в математическое моделирование / В.Н. Ашихмин [и др.]; под ред. П.В. Трусова. – М.: Логос, 2005. – 440 с.

3.Горстко А.Б. Познакомьтесь с математическим моделированием. –

М.: Знание, 1991. – 160 с.

195

4. Зубко И.Ю. Модель клеточных автоматов для монокристалла с дислокациями трех систем скольжения // Математическое моделирование: сб. науч. тр. Вып. 12. / Перм. гос. техн. ун-т. – Пермь, 2004. – С. 45–53.

5. Зубко И.Ю., Трусов П.В. Численное моделирование формирования дислокационных субструктур в поле примесных атомов // Вестник УГТУ-УПИ. Механика микронеоднородных материалов и разрушение: сб. науч. тр. / Урал. гос. техн. ун-т. – Екатеринбург; 2006. – № 11 (82). –

С. 70–76.

6.Максимей И.В. Имитационное моделирование на ЭВМ. – М.: Радио

исвязь, 1988. – 232 с.

7.Малинецкий Г.Г., Степанцов М.Е. Моделирование диффузионных процессов с помощью клеточных автоматов с окрестностью Марголуса // Журнал вычислительной математики и математической физики. – 1998. –

Т. 38, № 6. – С. 1017–1020.

8.Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа, 1998. – 319 с.

9.Тоффоли Т., Марголус Н. Машины клеточных автоматов. – М.: Мир,

1991. – 280 с.

196

ГЛАВА 4. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

Диапазон применения метода конечных элементов чрезвычайно широк: строительство и машиностроение, гидро- и аэродинамика, горное дело и новейшая техника, а также различные задачи математической физики – теплопроводности, механики деформируемого твердого тела, фильтрации, распространения волн и т. д.

Метод конечных элементов впервые был применен в инженерной практике в начале 50-х годов XX века. Первоначально он развивался по двум независимым один от другого направлениям – инженерному и математическому. Нараннем этапе формулировки МКЭ основывались на принципах строительной механики, что ограничивало сферу его применения. Итолько когда были сформулированы основы метода в вариационной форме, стало возможным распространение его на многие другие задачи. Быстрое развитие МКЭ шло параллельно с прогрессом современной компьютерной техники и ее применениемвразличныхобластях наукииинженернойпрактики.

Значительный вклад в разработку МКЭ был сделан Дж. Аргирисом. Им впервые дана общая матричная формулировка расчета стержневых систем на базе фундаментальных энергетических принципов, определена матрица податливости, а также введено понятие матрицы жесткости (как обратной матрице податливости). Работы Дж. Аргириса и его сотрудников, опубликованные в 1954–1960 годах, стала отправной точкой для матричной формулировки известных численных методов и применения ЭВМ в расчетах конструкций.

Для развития МКЭ особое значение имели вариационные принципы механики и математические методы, основанные на этих принципах. Дискретизацию задачи на основе вариационного метода Ритца впервые в 1943 г. применил Р. Курант. Лишь в 50-е годы появились аналогичные работы Ж. Поли, Ж. Герша и др.

Первая работа, в которой была изложена современная концепция МКЭ, относится к 1956 году. Американские ученые М. Тэрнер, Р. Клафф, Г. Мартин и Л. Топп, решая плоскую задачу теории упругости, ввели элемент треугольного вида, для которого сформировали матрицу жесткости и вектор узловых сил. Название метод конечных элементов ввел

в1960 году Р. Клафф. В период 1960–1965 годов опубликованы работы,

вкоторых на основе вариационных принципов получены конечные эле-

197

менты для решения задач изгиба плит, тонких оболочек, массивов. Среди них можно отметить работы Р. Мак-Лейа, Р. Мелоша, Дж. Бесселина, Ф. де Веубеке, М. Джонса, Т. Пиана. В 1967 году издана первая монография о МКЭ О. Зенкевича и И. Чанга, в которой изложены основы метода

иобласти его применения.

Ксемидесятым годам относится появление математической теории конечных элементов. Здесь можно выделить труды И. Бабушки, Р. Галлагера, Ж. Деклу, Дж. Одена, Г. Стренга, Дж. Фикса. Значительный вклад в разработку теоретических основ МКЭ внесли и российские ученые. В.Г. Корнеев указал на совпадение математической сущности МКЭ и ВРМ. Сопоставление МКЭ с рядом вариационных методов приведено в трудах Л.А. Розина. Под руководством А.С. Сахарова разработана моментная схема конечных элементов.

Последние десятилетия особенно отмечены развитием и применением МКЭ в таких областях механики сплошных сред, как оптимальное проектирование, учет нелинейного поведения, динамика конструкций и т.п.

Метод конечных элементов, как и многие другие численные методы, основан на представлении реальной континуальной конструкции ее дискретной моделью и замене дифференциальных уравнений, описывающих НДС сплошных тел, системой алгебраических уравнений. Вместе с тем МКЭ допускает ясную геометрическую, конструктивную и физическую интерпретацию [1].

4.1. ПРОЕКЦИОННЫЙ И ВАРИАЦИОННЫЙ ПОДХОДЫ

КПОСТРОЕНИЮ РАЗРЕШАЮЩИХ СООТНОШЕНИЙ МКЭ

Под термином метод конечных элементов (МКЭ) подразумевается семейство методов, основанных на проекционных методах решения уравнений или вариационных методах минимизации функционалов.

4.1.1. Проекционные методы. Основные понятия

Рассмотрим задачу о приближенном решении дифференциального уравнения [2]

F(u) = 0,

где оператор F: E → H и E, H – два бесконечномерных нормированных пространства. Пусть в пространствах E и H имеются базисы в следующем

смысле: существуют последовательности {φn }∞n=1 , {ψn }∞ n=1 , такие, что для

198

любых x E и y H найдутся числовые последовательности {α n}, {β n},

по нормам пространств E или H частичных сумм этих рядов). Введем последовательности конечномерных подпространств En и Hn, натянутых на первые n векторов, и обозначим через Pn и Qn операторы проектирования на эти пространства (En = Pn E, Hn = Qn H).

Суть проекционных методов состоит в замене дифференциального уравнения приближенным конечномерным уравнением

Fn (u ) = 0 ,

где u En , Fn : En → Hn , Fn = Qn F . Выбор разных базисов ϕ n, ψ n и разных проекторов приводит к разным проекционным методам.

В методе моментов (его также часто называют методом Петрова – Галеркина) решение дифференциального уравнения представляется в виде линейной комбинации n базисных функций пространства En:

нальна n базисным функциям пространства Hn: ψ 1, …, ψ n. Если бы функция была ортогональна всем функциям базиса H, то в сепарабельном пространстве она должна была обращаться в нуль, и тогда функция была бы точным решением. Поскольку вместо бесконечного набора базисных функций ограничиваются только п функциями, то полученное решение

n

будет приближенным. Условия ортогональности F (∑αiφi ) ψj пред-

i=1

ставляют собой n уравнений относительно неизвестных α 1, …, α n. Выражая из полученной системы числовые коэффициенты α i, найдем представление u .

В методе Галеркина пространства En и Hn совпадают, т.е. ϕ n = ψ n. Тогда общая схема построения приближенного решения уравнения F(u) = f – Lu = 0 следующая:

____

1. Выбор базисных функций φi , i = 1, n ;

2.Приближенное решение ищется в виде u = ∑αiφi ;

i=1n

199

3. Коэффициенты α i определяются из решения СЛАУ, полученной из условия ортогональности невязки и базисных функций:

____

( f − Lu ,φi ) = 0, (Lu ,φi ) = ( f ,φi ), i = 1, n .

СЛАУ имеет вид

При выборе различных весовых функций будут получаться различные проекционные методы.

4.1.2. Вариационные принципы

Во многих случаях задачу решения дифференциального уравнения можно заменить равносильной задачей об отыскании функции, сообщающей некоторому функционалу наименьшее или наибольшее значение. Задачи такого типа называются вариационными. Для некоторых физических задач более естественной является не дифференциальная постановка, а формулировка в виде вариационного принципа (естественный вариационный принцип). Например, если механическая система находится в равновесии, то ее потенциальная энергия минимальна, требуется минимизация потенциальной энергии системы. Вариационный принцип обычно формулируется в виде задачи минимизации интеграла от некоторой функции. Естественный вариационный принцип может быть сформулирован не для всех задач, но в то же время для одной и той же задачи может быть сформулировано несколько вариационных принципов. Если естественного вариационного принципа не существует, то его можно сконструировать с использованием метода множителей Лагранжа или метода штрафных функций, или метода наименьших квадратов. Применение вариационных принципов порождает ослабленную формулировку, когда соответствующее уравнение выполняется не в каждой точке тела, а в среднем, т.е. в некотором интегральном смысле [2].

Определение 1.

Оператор L: H → H (H – гильбертово пространство) называется симметричным, если (Lu, v) = (u, Lv), u, v H.

Определение 2.

Симметричный оператор L называется положительно определенным, если существует константа C > 0, такая, что (Lu,u ) ≥ C u 2 .

200