1311

x = xa sin(ωt +φx ),

где x – значение исследуемого параметра;

xa – амплитудное значение исследуемого параметра;

t– время;

φx – угол сдвига фазы исследуемого параметра.

Математическая модель позволила выявить существенное влияние реальных граничных условий на НДС образца-столбика и некорректность обычной экспериментальной процедуры определения параметров комплексного коэффициента Пуассона по формулам (1) без учета соответствующих поправок:

(µ* )Э = urb 2l0 , ux1 d0

(1)

(φµ )Э = φurb −φux1 +180,

где (µ* )Э , (φµ )Э – определяемые на базе обычной эксперименталь-

ной процедуры значения динамического коэффициента Пуассона и угла сдвига фазы между продольной и поперечной деформациями дополнительного к 180 градусам;

urb – амплитуда радиального смещения образца всреднем сечении; ux1 – амплитуда заданного осевого смещения образца;

l0 , d0 – начальная длина и диаметр образца;

φurb – угол сдвига фазы радиального смещения наружной поверхности образца в среднем сечении относительно фазы φux1 = 0 , за-

даваемого осевого смещения (в градусах).

После постановки математического эксперимента по разработанной модели была получена информация по величине базовых длин для

lБE = (E* )Эux1 ,

сДuД

∆φµ = (φµ )M −(φµ )Э,

∆φE = (φE )M −(φE )Э,

где (E* )Э , (φE )Э – определяемые на базе обычной экспериментальной

процедуры значения динамического модуля и угла сдвига фазы между напряжением и продольной деформацией;

(φµ )M , (φµ )E – углы сдвига фазы между напряжением и продоль-

ной деформацией, продольной и поперечной деформациями в материале соответственно;

∆φE , ∆φµ – соответствующие поправки по углам сдвига фазы; uД – амплитуда смещения датчика усилий.

Анализ результатов показал, что базовые длины и поправки по углам сдвига фазы зависят от параметров комплексного коэффициента Пуассона и динамического модуля, а поправка ∆φE несущественно от-

личается от поправки ∆φµ . С учетом этого, а также в силу того, что ре-

альные углы сдвига фазы между напряжением и деформацией более чем на порядок превышают величину самой поправки, было принято, что ∆φE ≈ ∆φµ . На основании регрессионного анализа результатов ма-

тематического эксперимента были получены феноменологические полиномиальные модели для lБE , lБµ , ∆φµ в зависимости от lg(E* )M ,

(µ* )M , (φE )M и (φµ )M .

Для определения истинных деформационных свойств вязкоупругих материалов (E* )M , (µ* )M , (φE )M и (φµ )M была предложена итера-

ционная процедура (обратная задача), связанная с последовательным уточнением базовых длин и поправки ∆φµ . Исходной информацией

для решения обратной задачи являются данные динамических опытов, проведенных по разработанному, близкого к D-оптимальному экспериментальному плану, включающему 9 точек факторного пространства «частота нагружения – температура опыта» и изначально принятые ба-

∆lБE = lБkE+1 −lБkE ≤ δ1,

∆lБµ = lБkµ+1 −lБkµ ≤ δ1,

∆φµk +1 −∆φµk ≤ δ2 ,

где δ1, δ2 – заданные точности определения базовых длин и поправ-

ки по углу сдвига фазы соответственно; k – номер итерации.

Для описания параметров комплексных операторов использовались полиномиальные зависимости, примененные ранее для комплексного модуля упругости [4], и, как показал регрессионный анализ, адекватные и для описания параметров комплексного коэффициента Пуассона в форме:

µ* = c0 +c1 lg ν′+c2 (lg ν′)2 +c3 (lg ν′)3 +c4 (lg ν′)4 ,

определяемые в результате параметрической идентификации.

По окончании итерационного процесса по откорректированным данным проводится повторная параметрическая идентификация поли-

упругости с использованием процедуры случайного поиска и алгоритма среднестатистического градиента. Повторная параметрическая идентификация может изменить начальный участок так, что

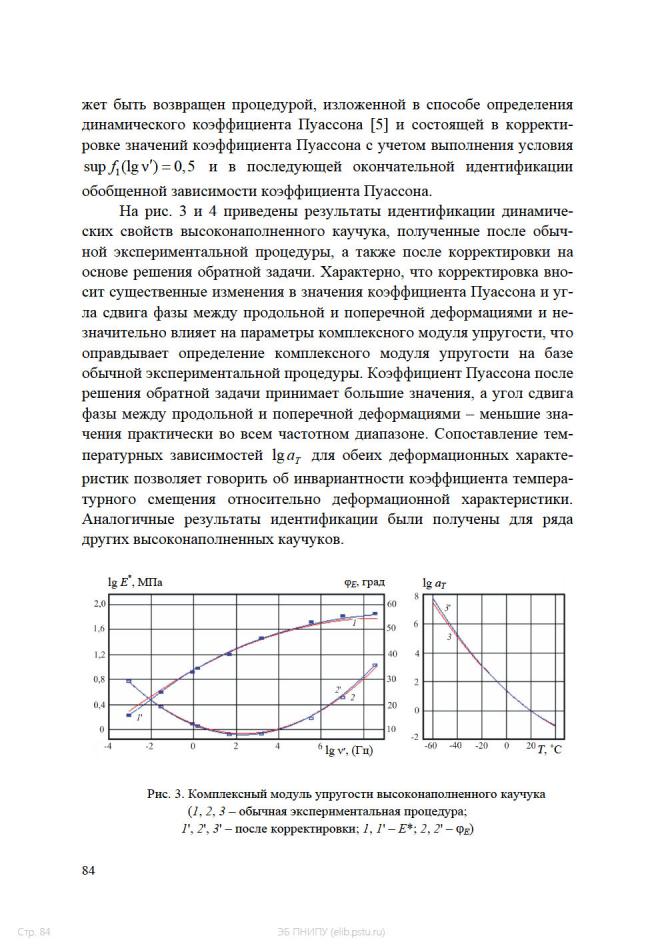
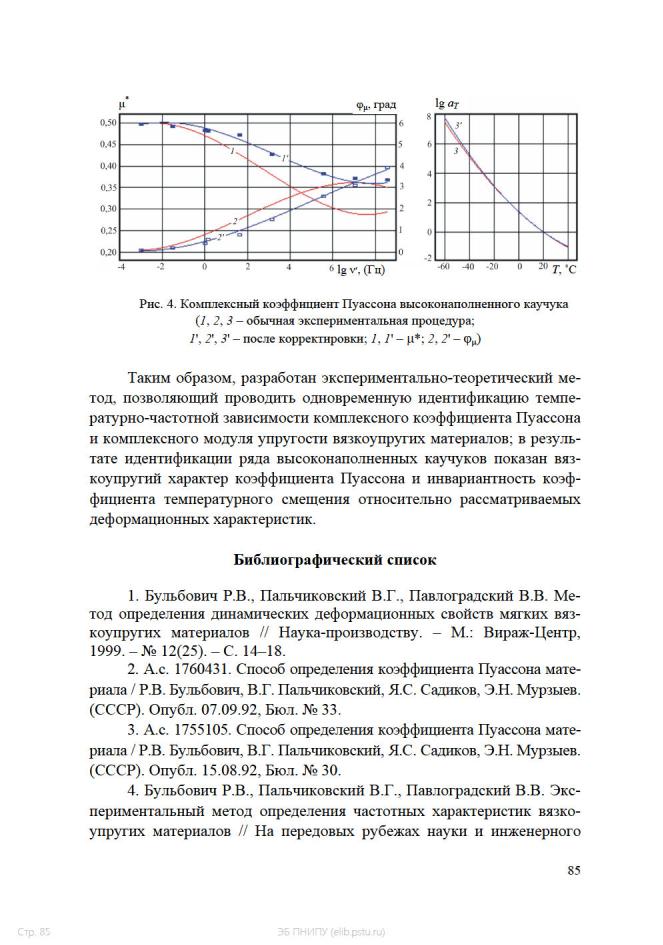
творчества: тр. 2-й междунар. НТК Регион. урал. отд. АИН. – Екатеринбург: Изд-во УГТУ, 2000. – 433 с.

5. А.с. 1827573. Способ определения динамического коэффициента Пуассона / Р.В. Бульбович, Э.Н. Мурзыев, В.В. Павлоградский, В.Г. Пальчиковский, Я.С. Садиков. (СССР). Опубл. 15.07.93, Бюл. № 26.

Получено 1.12.2010

86

Уравнение равновесия системы конечных элементов, находящейся в состоянии движения, имеет вид

где [K] – матрица жесткости конструкции;

[M ] – матрица масс конструкции;

{δ} – вектор неизвестных (перемещений и их производных);

{δ} – вектор узловых ускорений;

{R(t)} – вектор нагрузки в момент времени t .

Математически уравнение (2) представляет собой систему линейных дифференциальных уравнений второго порядка, и в принципе ее решение может быть получено с помощью стандартных процедур решения дифференциальных уравнений с постоянными коэффициентами. Однако эти процедуры становятся неэффективными при больших порядках матриц. Методы, используемые для решения уравнения (2), делятся на две группы: прямого интегрирования и разложения по собственным формам [2].

При прямом интегрировании уравнения (2) используется численная пошаговая процедура. Термин «прямое» означает, что перед интегрированием не производится никаких преобразований уравнений. Прямое интегрирование основано на двух идеях. Во-первых, удовлетворение условий равновесия (2) требуется не в любой момент времени t , а только на отдельных коротких отрезках времени ∆t . Это означает, что равновесие с учетом сил инерции рассматривается в дискретных точках временного интервала. Следовательно, становится возможным эффективное использование в методах прямого интегрирования всего вычислительного аппарата статистического анализа. Вовторых, учитывается изменение перемещений, скоростей и ускорений внутри каждого временного интервала ∆t . Именно способ учета этих изменений определяет точность, устойчивость и экономичность процедуры решения.

Использование прямого интегрирования эффективно, если требуется найти реакцию системы на сравнительно кратковременное воздействие (т.е. за несколько временных шагов). Однако при большом количестве шагов может оказаться более эффективным первоначаль-

89

ное преобразование уравнений равновесия (2) к виду, при котором пошаговое решение потребует наименьших затрат. При разложении перемещений по собственным формам колебаний уравнение равновесия

(2) приводится к n отдельным уравнениям вида

Соотношение (3) – уравнение равновесия системы с одной степенью свободы с единичной массой и жесткостью ωi2 .

Решение каждого уравнения (3) можно получить с помощью ин-

Интеграл Дюамеля должен в общем случае вычисляться численно. Для получения полной реакции системы необходимо найти решения всех n уравнений (3). Перемещения узловых точек получаются суперпозицией реакций системы по всем формам:

i=1

Таким образом, для получения реакции системы методом разложения по собственным формам требуется, во-первых, вычислить собственные значения и собственные векторы системы (2), затем решить уравнения равновесия (3) и, наконец, сложить реакции по каждой собственной форме в соответствии с (4).

Из методов прямого интегрирования наибольшее распространение нашли методы центральных разностей, метод Хаболта, θ-метод Вилсона и метод Ньюмарка [2]. В данной статье используется метод Ньюмарка как метод, обладающий лучшими характеристиками точности и устойчивости.

90