
Дискретная математика & математическая логика
..pdf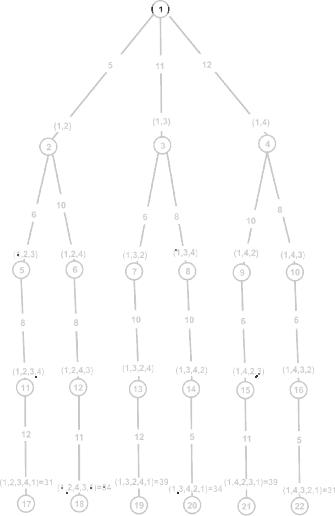
Рис. 4.2. Дерево перебора маршрутов в задаче коммивояжера
121
4.2. МЕТОД ВЕТВЕЙ И ГРАНИЦ
Метод ветвей и границ – общий алгоритмический метод для нахождения оптимальных решений различных задач оптимизации, особенно дискретной и комбинаторной оптимизации. По существу, метод является комбинаторным (алгоритм перебора) с отсевом подмножеств множества допустимых решений, не содержащих оптимальных решений. Метод был впервые предложен Ленд и Дойг в 1960 году для решения задач целочисленного линейного программирования. Для метода ветвей и границ необходимы две процедуры: ветвление и нахождение оценок (границ).
Процедура ветвления состоит в разбиении области допустимых решений на подобласти меньших размеров. Процедуру можно рекурсивно применять к подобластям. Полученные подобласти образуют дерево, называемое деревом поиска или деревом ветвей и границ. Узлами этого дерева являются построенные подобласти.
Процедура нахождения оценок заключается в поиске верх-
них и нижних границ для оптимального значения на подобласти допустимых решений.
В основе метода ветвей и границ лежит следующая идея (для задачи минимизации): если нижняя граница для подобласти A дерева поиска больше, чем верхняя граница какой-либо ранее просмотренной подобласти B, то A может быть исключена из дальнейшего рассмотрения (правило отсева). Обычно минимальную из полученных верхних оценок записывают в глобальную переменную m; любой узел дерева поиска, нижняя граница которого больше значения m, может быть исключен из дальнейшего рассмотрения.
Если нижняя граница для узла дерева совпадает с верхней границей, то это значение является минимумом функции и достигается на соответствующей подобласти.
Рассмотрим частный случай метода ветвей и границ.
Метод половинного разбиения при поиске отказов в ком-
пьютерных системах. Иногда возможно проверять компоненты не по одному, а группой. Проверим наличие тока через последова-
122

тельную цепь для обнаружения обрыва. Количество компонентов n можно выразить как
n = 2m + r ,
где r – « остаток» до соответствующей степени числа 2,
n − r = 2m.
Например, при n = 5 m = 2 , r =1 .
Построим дерево проверок для n = 5 (рис. 4.3):
Рис. 4.3. Дерево проверок для n = 5
Минимальное количество проверок Nmin = 2 = m. Максимальноеколичествопроверок Nmax = 3 = m +1 (for _ r ≠ 0). При m проверках распознается n − 2r технических состояний
(при n = 5 – три состояния).
123
При (m +1)-й |
проверке распознается 2r |
технических состоя- |
||||||||||||||||||||||||||||||
ний (при (n + 5)-й – |
два состояния). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
При r = 0 n состояний распознается при m проверках. Тогда |
||||||||||||||||||||||||||||||||
Nmin = Nmax = m . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получим среднее число проверок |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
n−2r |
|
|
|
|
|
|
|
|
|
|
2r |
|
|
|
|||||||||||
|
|
Nср = m |
∑ qi + (m +1)∑qi , |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|||||||||
где qi – вероятность нахождения в i-м техническом состоянии. |
||||||||||||||||||||||||||||||||
При равновероятных состояниях qi |
= |
1 |
|
: |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||
|
n−2r |
1 |
|
|
|
|
|
|
|
2r |
1 |
|
|
|
|
n − 2r |
|
|
|
2r |
|
|||||||||||
Ncp = m ∑ |
+ (m +1)∑ |
= m |
+ (m +1) |
= |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
i=1 |
n |
|
|
i=1 |
n |
|
|
|
|
n |
|
n |
|||||||||||||||||||
= |
mn − 2mr + 2mr + 2r |
|
= m + |
2r |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||||
Например, при n = 5 |
m = 2 , r =1 : |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Nср = |
2 |
+ |
2 |
+ |
2 |
+ |
3 |
+ |
3 |
= |
12 |
= 2, 4. |
|||||||||||||||||||
|
|
5 |
|
|
|
5 |
|
|||||||||||||||||||||||||
|
|
5 |
|
5 |
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
||||||||||||||
Или Nср = m + |
2r |
= 2 + |
2 1 |
= 2, 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
n |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Причем необязательно разбивать множество на одинаковое число компонентов. Достаточно, чтобы количество компонент в «длинном» участкеnд соответствоваловыражению
2m−1 < nд ≤ 2m ,
а в «коротком» участке
nк ≥ 2m−1 .
Естественно, что
nд + nк = n.
124

Полученные результаты могут использоваться для иллюстрации метода оптимизации, называемого методом ветвей и границ. Функция предпочтения – это, например, показания прибора, определяющего наличие тока, или диагностической аппаратуры, формирующей сообщение «есть отказ – нет отказа».
Задача о рюкзаке [8]
Перед туристическим походом в рюкзак вместимостью не более А единиц веса из набора I = {1, 2, 3, …, n} предметов, каждый весом аi и ценностью сi необходимо положить такие предметы, которые максимизируют суммарную ценность груза и по весу вмещаются в рюкзак. «Рюкзак» может толковаться как полезный груз, выводимая на орбиту ракета, как кузов грузовой машины и пр.
Пусть допустимый вес рюкзака V = 15. Количество предметов n = 5. Вес предметов 3, 2, 4, 5, 6. Ценность предметов соответствен-
но 6, 5, 6, 12, 10.
Определим ценность единиц грузов: 6/3, 5/2, 6/4, 12/5, 10/6. Получим следующие показатели ценности: 2; 2,5; 1,5; 2,4; 1,67. Упорядочим ценности по убыванию: 2,5; 2,4; 2; 1,67; 1,5. Составим таблицу исходных данных к задаче о ранце:
|
|
аi |
|
а2 |
|
|
|
а4 |
|
а1 |
|
а5 |
|
|
|
а3 |
|||||||||||
|
|
|
|
|
2 |
|
5 |
|
|
|
|
3 |
|
|
|
6 |
|
|
4 |
|
|||||||
|
|
сi |
|
с2 |
|
|
|
с4 |
|
с1 |
|
с5 |
|
|
|
с3 |
|||||||||||
|
|
|
|
|
5 |
|
12 |
|
|
|
|
6 |
|
|
|
10 |
|
|
6 |
|
|||||||
|
|
хi |
|
х2 |
|
|
|
х4 |
|
х1 |
|
х5 |
|
|
|
х3 |
|||||||||||
Построим таблицу вариантов (всего 32): |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
№ |
х1 |
|
х2 |
|
|
х3 |
|
х4 |
|
|
х5 |
|
А |
|
С |
||||||||||
|
0 |
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
0 |
|
0 |
|
0 |
|
|
0 |
|
|||||
|
31 |
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
20 > 15 |
|
|
– |
||||||
|
|
30 |
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
0 |
|
|
14 |
|
|
|
29 |
|
|
29 |
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
0 |
|
1 |
|
15 |
|
|
33 |
|
|||||
|
28 |
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
0 |
|
0 |
|
9 |
|
|
17 |
|
|||||
|
21 |
|
|
1 |
|
|
|
0 |
|
1 |
|
|
|
0 |
|
1 |
|
13 |
|
|
22 |
|
|||||
125
В данной задаче можно относительно быстро подобрать оптимальный вариант № 30 без сложных процедур ветвления.
4.3. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Линейное программирование – математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно – основа нескольких методов решения задач целочисленного и нелинейного программирования.
Пусть система ограничений (уравнений) имеет вид
−2x1 + x2 + x3 = 2, |
|
|
||
|
− 2x2 + x4 = 2, |
|
|
|
x1 |
|
|
||
x1 + x2 + x5 = 5, |
|
|
||
q |
'= −q = − (x |
− x |
)= x − x |
→ max. |
|
2 |
1 |
1 |
2 |
Здесь три уравнения и пять неизвестных. Выразим переменные х3, х4, х5 через х1, х2:
x3 = 2 + 2x1 − x2 , |
|||
x4 |
= 2 − x1 + 2x2 , |
||
x5 |
= 5 − x1 − x2 , |
→ max. |
|
|
1 |
2 |
|
q '= −q = x − x |
|
||
Учитывая, что х3, х4, х5, получим геометрическую интерпретацию задачи оптимизации – рис. 4.4.
126

Рис. 4.4. Геометрическая интерпретация задачи оптимизации х1 = 4, х2 = 1
Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.
Для решения оптимизационной задачи алгебраически предложен так называемый симплекс-метод.
Симплекс, или n-симплекс, это геометрическая фигура, являющаяся n-мерным обобщением треугольника. Определяется как выпуклая оболочка n + 1 точек, не лежащих в одной n-мерной гиперплоскости (рис. 4.5).
Рис. 4.5. n-Симплекс
127
Эти точки называются вершинами симплекса, в частности:
–0- симплекс – точка,
–1- симплекс – отрезок,
–2- симплекс – треугольник,
–3- симплекс – тетраэдр.
Выпуклая оболочка любых m + 1 из n + 1 вершин n-симплек- са сама является симплексом и называется m-гранью симплекса. 0-грани – это вершины, 1-грани – это рёбра, n–1- грани называют просто гранями. Стандартный симплекс представлен на рис. 4.6.
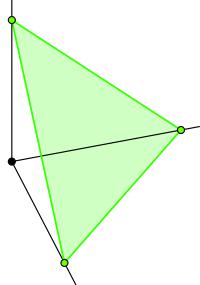
Рис. 4.6. Стандартный 2-симплекс – зелёный треугольник
Симплекс-метод – алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан американским математиком Джорджем Данцигом (George Dantzig,
рис. 4.7) в 1947 году.
128

Рис. 4.7. Джордж Данциг
Существо симплекс-метода состоит в следующем. Прежде всего, находится некоторое допустимое – базисное решение. Его можно найти, приняв какие-либо n – m переменных за свободные, приравняв их к нулю и решив получившуюся систему уравнений. Напомним, что n – число неизвестных, а m – число уравнений.
Если после этого некоторые базисные переменные окажутся отрицательными, то нужно выбрать другие свободные переменные, т.е. перейти к новому базису.
После того как найдено допустимое базисное решение, проверяется, не достигнут ли максимум целевой функции. Если нет, то ищут новое допустимое базисное решение, но не любое, а такое, которое увеличивает значение целевой функции, после чего процедура повторяется.
Рассмотрим ту же систему уравнений, для которой надо найти неотрицательное решение:
−2x1 + x2 + x3 = 2, |
|
|
|
||
|
− 2x2 + x4 = 2, |
|
|
|
|
x1 |
|
|
|
||
x1 + x2 + x5 = 5, |
|
|
|
||
q' |
= −q = −(x |
− x ) = x |
− x |
→ max. |
|
|
2 |
1 |
1 |
2 |
|
129
Ввиду того, что n – m = 2, в качестве свободных можно взять,
например, х1, х2.
Приравняв их нулю, находим базисное решение
x1 = 0, |
|
|
|
x2 |
= 0, |
|
|
x3 = 2, |
|
|
|
x4 |
= 2, |
|
|
x5 |
= 5, |
|
|
|
1 |
2 |
= 0. |
|
|||
q' |
= x |
− x |
|
Это решение допустимо, поскольку переменные неотрицательны. Проверку того, не достигнут ли максимум, можно выполнить путём поиска нового допустимого базисного решения, при котором целевая функция будет больше.
Для перехода к новому допустимому базисному решению одну из свободных переменных х1, х2 следует сделать базисной. В нашем примере переменная х1 входит в выражение целевой функции со знаком +. Значит, максимум целевой функции не достигнут, и переменную х1 следует сделать базисной. Возьмём систему уравнений
x3 |
= 2 + 2x1 − x2 , |
|
|
x4 |
= 2 − x1 + 2x2 , |
|
|
x5 = 5 − x1 − x2 , |
→ max. |
||
|
1 |
2 |
|
q' |
= −q = x − x |
|
|
При х2 = 0 увеличение х1 не приводит к уменьшению х3, но уменьшаетх4, х5, такчто прих1 = 2 получим
x1 = 2,
x2 = 0,
x3 = 6,
x4 = 0,x5 = 3,
q' = x1 − x2 = 2.
130
