
Дискретно-полевые модели электрических машин. Часть I II
.pdfражениями и получаем систему алгебраических уравнений, записываемых в виде
U it,+j1 −U it, j |
= |
Uit+1, j |
− 2Uit, j |
+ Uit−+1,1 j |
+ |
Uit, j +1 |
− 2Uit, j |
+ Uit,+j1−1 |
+ f |
t +0,5 |
||||||
|
τ |
|
|
|
h2 |
|
|
|
h2 |
|
|
|
i, j |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
t |
t +1 |
|
t |
− |
t |
|
t +1 |
|
|
|
|
U it,+j1 =U it, j |
+ τ |
Ui+1, j − 2Ui, j |
+Ui−1, j |
+ |
Ui, j+1 |
2Ui, j |
+Ui, j−1 |
+ |
f it,+j0,5 . |
||||||
|
|
|
|
|
h2 |
|
||||||||||
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Плотность источников задана в виде |
|
|
|
|
|
|
|
|||||||||
|
f [1: N +1, 1: N +1] = 0 ; |
f [8 :10, 8 :10 =100]. |
|
|
||||||||||||
Используя начальные, граничные условия и известные значения плотности источников, рассчитываем значения искомой функции на каждом временном слое, пока не будет достигнуто конечное время расчёта.
Программа решения двумерной краевой задачи с использованием явной схемы:
n1=17; n2=17; hx=1./(n1-1); hy=1./(n2-1); dt=0.0009; k1=dt/hx^2;.; t=0.; a(1: n1,1: n2)=0.; a0(1: n1,1: n2)=0.; f(1: n1,1: n2)=0.; f(8: 10,8: 10)=100n=1; nk=600;
while n<nk for i=2: n1-1
for j=2: n2-1
r1=a0(i+1,j)-2.*a0(i,j)+a0(i-1,j); r2=a0(i,j+1)-2.*a0(i,j)+a0(i,j-1); a(i,j)=a0(i,j)+k1*(r1+r2+f(i,j)*hx^2);
end end
disp(n); disp(a(9,9)); x(n)=n; y(n)=a(9,9); a0(1: n1,1: n2)=a(1: n1,1: n2); n=n+1; end
plot(x,y); disp(a)
91

Результаты решения краевой задачи U (x, y) (установившийся режим):
i = 1…9
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,0149 |
0,0298 |
0,0446 |
0,0589 |
0,0720 |
0,0828 |
0,0901 |
0,0927 |
0 |
0,0298 |
0,0597 |
0,0896 |
0,1189 |
0,1462 |
0,1692 |
0,1849 |
0,1905 |
0 |
0,0446 |
0,0896 |
0,1353 |
0,1810 |
0,2248 |
0,2629 |
0,2898 |
0,2996 |
0 |
0,0589 |
0,1189 |
0,1810 |
0,2450 |
0,3090 |
0,3678 |
0,4119 |
0,4283 |
0 |
0,0720 |
0,1462 |
0,2248 |
0,3090 |
0,3983 |
0,4876 |
0,5616 |
0,5897 |
0 |
0,0828 |
0,1692 |
0,2629 |
0,3678 |
0,4876 |
0,6225 |
0,7574 |
0,8071 |
0 |
0,0901 |
0,1849 |
0,2898 |
0,4119 |
0,5616 |
0,7574 |
1,0384 |
1,1241 |
0 |
0,0927 |
0,1905 |
0,2996 |
0,4283 |
0,5897 |
0,8071 |
1,1241 |
1,2217 |
0 |
0,0901 |
0,1849 |
0,2898 |
0,4119 |
0,5616 |
0,7574 |
1,0384 |
1,1241 |
0 |
0,0828 |
0,1692 |
0,2629 |
0,3678 |
0,4876 |
0,6225 |
0,7574 |
0,8071 |
0 |
0,0720 |
0,1462 |
0,2248 |
0,3090 |
0,3983 |
0,4876 |
0,5616 |
0,5897 |
0 |
0,0589 |
0,1189 |
0,1810 |
0,2450 |
0,3090 |
0,3678 |
0,4119 |
0,4283 |
0 |
0,0446 |
0,0896 |
0,1353 |
0,1810 |
0,2248 |
0,2629 |
0,2898 |
0,2996 |
0 |
0,0298 |
0,0597 |
0,0896 |
0,1189 |
0,1462 |
0,1692 |
0,1849 |
0,1905 |
0 |
0,0149 |
0,0298 |
0,0446 |
0,0589 |
0,0720 |
0,0828 |
0,0901 |
0,0927 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
i = 10…17
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,0901 |
0,0828 |
0,0720 |
0,0589 |
0,0446 |
0,0298 |
0,0149 |
0 |
0,1849 |
0,1692 |
0,1462 |
0,1189 |
0,0896 |
0,0597 |
0,0298 |
0 |
0,2898 |
0,2629 |
0,2248 |
0,1810 |
0,1353 |
0,0896 |
0,0446 |
0 |
0,4119 |
0,3678 |
0,3090 |
0,2450 |
0,1810 |
0,1189 |
0,0589 |
0 |
0,5616 |
0,4876 |
0,3983 |
0,3090 |
0,2248 |
0,1462 |
0,0720 |
0 |
0,7574 |
0,6225 |
0,4876 |
0,3678 |
0,2629 |
0,1692 |
0,0828 |
0 |
1,0384 |
0,7574 |
0,5616 |
0,4119 |
0,2898 |
0,1849 |
0,0901 |
0 |
1,1241 |
0,8071 |
0,5897 |
0,4283 |
0,2996 |
0,1905 |
0,0927 |
0 |
1,0384 |
0,7574 |
0,5616 |
0,4119 |
0,2898 |
0,1849 |
0,0901 |
0 |
0,7574 |
0,6225 |
0,4876 |
0,3678 |
0,2629 |
0,1692 |
0,0828 |
0 |
0,5616 |
0,4876 |
0,3983 |
0,3090 |
0,2248 |
0,1462 |
0,0720 |
0 |
0,4119 |
0,3678 |
0,3090 |
0,2450 |
0,1810 |
0,1189 |
0,0589 |
0 |
0,2898 |
0,2629 |
0,2248 |
0,1810 |
0,1353 |
0,0896 |
0,0446 |
0 |
0,1849 |
0,1692 |
0,1462 |
0,1189 |
0,0896 |
0,0597 |
0,0298 |
0 |
0,0901 |
0,0828 |
0,0720 |
0,0589 |
0,0446 |
0,0298 |
0,0149 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
92
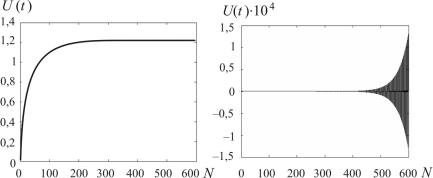
а |
б |
Рис. 4.1. Результат решения двумерной краевой задачи:
а− при выполнении условия устойчивости ( τ = 0, 0009 ); б − при нарушении условия устойчивости ( τ = 0, 001 )
На рис. 4.1 представлено решение смешанной краевой задачи, выполненной по явной схеме для устойчивого варианта, когда временной интервал соответствует условию устойчивости, и неустойчивого варианта, когда условие устойчивости не выполнено.
4.1.2. Неявная схема
Для неявной схемы дифференциальное уравнение записывается следующим образом:
U it,+j1 −U it, j |
= K1 |
Uit++1,1 j − 2Uit,+j1 +Uit−+1,1 j |
+ K 2 |
Uit,+j1+1 − 2Uit,+j1 +Uit,+j1−1 |
+ τ |
f it |
, j |
+ f it,+j1 |
||
|
|
|
|
|
|
|
. |
|||
τ |
|
h2x |
h2y |
|
|
2 |
||||
|
|
|
|
|
|
|
||||
|
|
|
i = 1, 2, ..., N 1 −1; j = 1, 2, ..., N 2 −1 . |
|
|
|
(4.5) |
|||
Полученную систему можно преобразовать к виду |
|
|
|
|
|
|||||
|
Ai, jU it ++1,1 |
j + Bi, jU it−+1,1 j + C i, jU it,+j1+1 + Di, jU it,+j1−1 − F i, jU it,+j1 = ϕ i, j |
|
(4.6) |
||||||
|
|
|
|
|
|
|
|
|
93 |
|

для тех же значений i, j . В этом случае на каждом временном слое необходимо решать систему N 1N 2 алгебраических уравнений. Положим для упрощения N 1 = N 2 = N . Тогда число неизвестных будет
равным N 2 . Матрица системы является разреженной, причём отлич-
ные от нуля элементы расположены лишь на пяти диагоналях. Для решения такой системы с учётом слабого заполнения ленточной мат-
рицы потребуется ~ N 4 операций. Для неявных схем временной шаг можно выбирать произвольно. Поэтому для достижения конечного времени счёта потребуется выполнить T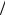 τ шагов по времени. В этом
τ шагов по времени. В этом
случае время решения краевой задачи будет пропорционально Tτ N 4 .
Пример 4.2. Решение смешанной краевой задачи с использо-
ванием неявной схемы. В квадрате [0:1, 0:1] решим смешанную краевую задачу
∂ U |
= |
|
∂ 2U |
+∂ |
2U |
+ f ( x, y ) |
|
∂ x2 |
∂ y2 |
||||
∂ t |
|
|
||||
при нулевых начальных и граничных условиях:
U (x, y,0) = 0 ; U (0, y,t) = U (1, y,t) = U (x,0,t) = U (x,1,t) = 0 .
Для решения задачи используем неявную схему.
Программа решения двумерной краевой задачи с использованием неявной схемы:
n1=17; n2=17; dn=16; hx=1./(n1-1); hy=1./(n2-1); dt=0.001; nk=500; y(1:nk)=0; z(1:nk)=0; k1=dt/(hx*hx); k2=1.+4.*k1; a(1:225,1:225)=0.; f(1:225)=0.; x0(1:225)=0; i1=17; i2=29;
f(97:99)=-100.*dt; f(112:114)=-100.*dt; f(127:129)=-100.*dt; t=0.; n=0; t0=0.; while i1<212
for i=i1:i2
a(i,i-15)=k1; a(i,i-1)=k1; a(i,i)=-k2; a(i,i+1)=k1; a(i,i+15)=k1;
end
i1=i1+15; i2=i2+15; end
for i=16:15:196
a(i,i-15)=k1; a(i,i)=-k2; a(i,i+1)=k1; a(i,i+15)=k1;
end
94
for i=30:15:210
a(i,i-15)=k1; a(i,i-1)=k1; a(i,i)=-k2; a(i,i+15)=k1;
end
for i=2:14
a(i,i-1)=k1; a(i,i)=-k2; a(i,i+1)=k1; a(i,i+15)=k1; end
for i=212:224
a(i,i-15)=k1; a(i,i-1)=k1; a(i,i)=-k2; a(i,i+1)=k1;
end
a(1,1)=-k2; a(1,2)=k1; a(1,16)=k1; a(15,15)=-k2; a(15,14)=k1; a(15,30)=k1; a(211,212)=k1; a(211,211)=-k2; a(211,196)=k1; a(225,225)=-k2; a(225,224)=k1; a(225,210)=k1;
while n<nk
fk(1:225)=-x0(1:225)+f(1:225); x=fk/a; x0(1:225)=x(1:225); t=t0+dt*n; n=n+1; y(n)=x(113);
z(n)=n; disp(n); disp(x(113)); end
disp(x); plot(z,y)
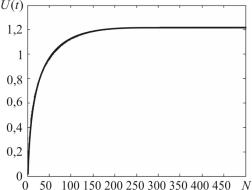
Установившиеся значения искомой величины, полученные при решении краевой задачи с использованием явной и неявной схем, полностью совпадают. Неявная схема является безусловно устойчивой. На рис. 4.2 показан характер переходного процесса при τ > τ0 .
Для явной схемы при такой величине временного интервала τ переходный процесс является расходящимся (рис. 4.1, б).
Рис. 4.2. Результаты решения смешанной краевой задачи с использованием неявной схемы ( τ = 0, 001)
95
Приведённые рассуждения показывают, что как явная, так и неявная схемы не экономичные: число математических операций на одно неизвестное не является постоянным. Однако для решения многомерных уравнений параболического типа существуют экономичные схемы с затратой постоянного числа операций на одну точку исследуемой области, к которым относится рассматриваемый ниже метод переменных направлений.
4.2. МЕТОД ПЕРЕМЕННЫХ НАПРАВЛЕНИЙ
Одним из наиболее часто используемых на практике методов решения нестационарных краевых задач является метод переменных на-
правлений, называемый часто продольно-поперечной схемой [23, 24, 25].
Решение задачи с использованием этого метода производится следующим образом. Временной интервал разбивается на два полуцелых слоя, и на каждом из них решается краевая задача с использованием неявной схемы по одной координате и явной – по другой. Полученное при этом решение принимается в качестве начального для второго полуцелого временного слоя, на котором меняются направления явной и неявной схем. Дифференциальное уравнение при этом заменяется двумя конечно-разностными уравнениями:
|
|
|
|
|
|
|
|
t +0,5 |
|
|
|
t +0,5 |
|
t +0,5 |
|
|
||
1 |
(U it,+j0,5 −U it, j ) = k1 |
Ui+1, j |
− 2Ui, j |
|
+ Ui −1, j |
+ |
||||||||||||
0,5τ |
|
|
|
|
|
h2x |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.7) |
|||
|
|
U t |
− 2U t |
+ U t |
|
|
|
f t |
+ f t +1` |
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
+k 2 |
|
i, j +1 |
i, j |
|
|
i, j −1 |
+ |
|
i, j |
|
i, j |
; |
|
|
|||
|
|
|
h2y |
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
t +0,5 |
|
|
|
t +0,5 |
|
t +0,5 |
|
|
||
1 |
(U it,+j1 |
−U it |
,+j0,5 ) = k1 |
Ui+1, j |
− 2Ui, j |
|
+ Ui −1, j |
|
+ |
|||||||||
0,5τ |
|
|
|
|
h2x |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.8) |
|||
|
U t +1 |
− 2U t +1 |
+ U t +1 |
|
|
|
f t |
+ f t +1` |
||||||||||
|
|
|
|
|
|
|||||||||||||
|
+k 2 |
|
i, j +1 |
i, j |
|
|
i, j −1 |
+ |
|
i, j |
|
i, j |
. |
|
|
|||
|
|
|
h2y |
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
96
Первое из |
этих уравнений содержит |
три неизвестные |
||||
U it ++1,0,5j , U it,+j0,5, U it−+1,0,5j , |
значения |
величин |
второй |
группы |
U it, j +1, U it, j, |
|
U it, j −1 известны |
из |
решения |
задачи |
на предыдущем |
временном |
|
слое или из начальных условий при начале счёта. Поэтому первое уравнение может быть решено методом прогонки вдоль направления координаты i для всех значений j =1, 2, ..., N2 −1 . Точно так
же для второго уравнения (4.8) неизвестными величинами будут
U t +1+ , U t +1, U t +1− , а значения U t +0,5, U t +0,5, U t +0,5 определены на
i, j 1 i, j i, j 1 i+1, j i, j i −1, j
предыдущем полуслое. Второе уравнение решается методом прогонки вдоль направления координаты j для всех значений
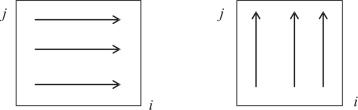
i =1, 2, ..., N1 −1 (рис. 4.3).
Рис. 4.3. К решению краевой задачи методом переменных направлений
Оценим погрешность метода переменных направлений. Обозна-
чив дискретные операторы Лапласа как |
∆ |
1 и ∆ |
2 , |
суммируя уравне- |
||||||||||||||
ния (4.7) и (4.8), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
U it,+j1 −U it, j |
|
|
t + |
0,5 |
|
|
(U |
t +1 |
|
t |
+) |
|
t +0,5 |
|
|
|||
|
|
|
= ∆ |
U |
i, j |
+ |
0,5∆ |
2 |
+ |
U |
|
f |
i, j |
. |
(4.9) |
|||
|
|
|
|
|||||||||||||||
|
τ |
|
|
1 |
|
|
|
|
i, j |
|
i, j |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим U it,+j0,5 , вычитая из уравнения (4.8) уравнение (4.7): |
||||||||||||||||||
|
Uit,+j |
0,5 = 0,5 |
(Uit,+j1 +Uit, j ) − |
τ |
∆ 2 (Uuit,+j1− U it, j) . |
|
(4.10) |
|||||||||||
|
4 |
|
||||||||||||||||
Подставляя полученное выражение в (4.9), будем иметь
97
U it ,+j1 −U it , j |
|
|
|
|
|
|
t +1 |
|
t |
|
t +1 |
t |
||||
|
|
|
= 0,5∆ 1 |
(Ui, j + |
Ui, j )+ |
0,5∆ 2 (Ui, |
+j |
Ui, j−) |
||||||||
|
|
τ |
||||||||||||||
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
(4.11) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
t +1 |
|
t |
|
t +0,5 |
|
|
|||
|
|
|
− ∆ ∆1 2 |
|
(Ui , j |
− Ui, j ) |
+ |
f i. j |
|
|
||||||
|
|
|
4 |
|
|
|||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
U i,jt +1 −U it, j |
|
|
|
|
|
|
|
|
t 1 |
|
|
|
t |
||
|
|
|
|
= |
0,5 |
(∆ 1+ ∆ |
2 )U i ,+j |
|
0,5∆( +1∆ |
|
2 )U+i , j |
|||||
|
|
τ |
|
|
|
|||||||||||
|
|
|
t +1 |
|
|
|
|
|
|
|
|
|
|
|
(4.12) |
|
|
|
|
f |
+ f |
t |
|
|
|
τ |
(Uit,+j1 − Uit, j ). |
|
|||||
|
|
|
|
|
|
|
|
|||||||||
+ |
|
i , j |
|
|
i, j |
− ∆ ∆1 |
2 |
|
|
|||||||
|
|
2 |
|
|
4 |
|
|
|||||||||
В этом уравнении все члены за исключением последнего образуют симметричную неявную схему, рассмотренную ранее, обладающую вторым порядком точности, как по временной координате, так и по пространственным. Дискретный оператор Лапласа обеспечивает второй порядок точности по пространственной координате. Следовательно, последний член этого выражения обладает четвёртым порядком по пространственным координатам. Для определения погрешности этого члена по временной координате разложим функ-
ции U it,+j1 и U it, j |
в ряд Тейлора в окрестности точки U it,+j0,5 : |
||||||||||||||||||||||
|
|
|
τ |
|
∂ U |
t +0,5 |
|
1 |
|
τ |
2 |
|
|
2 |
|
|
t +0,5 |
|
|||||
t +1 |
t +0,5 |
|
|
|
|
|
∂ |
U |
|
|
|
||||||||||||
U i, j |
= U i, j |
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
+ ...; |
2 |
|
|
|
2 |
|
|
∂ |
t |
2 |
||||||||||||||
|
|
|
|
∂ t i, j |
|
|
|
2 |
|
|
|
|
i, j |
|
|||||||||
|
|
|
τ |
|
∂ U |
t + |
0,5 |
|
1 |
|
τ |
2 |
|
|
2 |
|
|
t +0,5 |
|
||||
t |
t +0,5 |
|
|
|
|
|
∂ |
U |
|
|
|
||||||||||||
U i, j |
= U i, j |
− |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
+ ... |
2 |
|
|
|
|
2 |
|
|
|
∂ |
t |
2 |
|
|||||||||||
|
|
|
|
∂ t i, j |
|
|
2 |
|
|
|
|
i, j |
|
||||||||||
Тогда
|
,+j1 −U it |
|
∂ U t +0,5 |
|
|
U it |
, j = τ |
|
|
+ ... |
|
|
|||||
|
|
|
∂ t i , j |
|
|
и последний член уравнения (4.12) может быть записан в виде
|
τ2 |
∂ U t +0,5 |
+ ... , |
||
∆ ∆1 2 |
|
|
|
|
|
4 |
|
||||
|
|
∂ t i, j |
|
||
т.е. имеет второй порядок точности по временной координате.
(4.13)
(4.14)
(4.15)
(4.16)
98
При решении одномерных краевых задач методом прогонки приходится использовать граничные условия (4.2). Если значения функции на границах от времени не зависят, то проблем с их заданием для любого момента времени не возникает. Точно так же значения функций на границах однозначно определены в моменты времени, соответствующие целочисленным слоям t, t +1, t + 2, ... В этом случае
величина (x,t) задаётся для соответствующего момента времени.
Если |
же рассматриваются промежуточные временные |
слои |
t + 0,5; |
t +1,5; t + 2,5... , то граничные значения функций (x,t) |
так- |
же должны соответствовать этим моментам времени. Принимая граничные значения, соответствующие целочисленным моментам времени, мы допускаем погрешность, так как на промежуточных временных слоях значения функций должны соответствовать выражению (4.10). Поэтому, чтобы обеспечить второй порядок точности по временной координате, граничные условия на промежуточных временных слоях рассчитываются для обеих границ как
µt +0,5 = 0,5(µt +1 + µt ) − |
τ |
∆ |
2 (µt +1 − µt ) . |
(4.17) |
|
||||
4 |
|
|
|
|
При этих условиях метод переменных направлений обеспечивает второй порядок точности, как по пространственным, так и по временной координате.
Пример 4.3. Решение смешанной краевой задачи методом пе-
ременных направлений. В качестве примера используем краевую задачу, рассмотренную в предыдущих разделах.
В квадрате [0:1,0:1] решить смешанную краевую задачу
∂ U |
= |
|
∂ 2U |
+∂ |
2U |
+ f ( x, y ) |
|
∂ x2 |
∂ y2 |
||||
∂ t |
|
|
||||
при нулевых начальных и граничных условиях:
U (x, y,0) = 0 ; U (0, y,t) = U (1, y,t) = U (x,0,t) = U (x,1,t) = 0 .
В соответствии с изложенным выше, дифференциальное уравнение записывается в виде двух конечно-разностных:
99
|
|
|
|
t +0,5 |
t +0,5 |
t +0,5 |
1 |
|
(U it,+j0,5 −U it, j ) = |
Ui +1, j |
− 2Ui, j |
+ Ui −1, j |
|
0,5τ |
|
|
h2 |
|
||
|
|
|
|
|
||
|
|
|
|
t +0,5 |
t +0,5 |
t +0,5 |
1 |
|
(U it,+j1 −U it,+j0,5 ) = |
Ui+1, j |
− 2Ui, j |
+ Ui −1, j |
|
0,5τ |
|
|
h2 |
|
||
|
|
|
|
|
||
|
|
U t |
− 2U t |
+ U t |
|
|
+ |
|
i, j +1 |
i , j |
i, j −1 |
|
+ f it , j |
|
|
h2 |
|
|||
|
|
|
|
|
|
|
|
U t +1 |
− 2U t +1 |
+ U t +1 |
|
|
|
+ |
|
i, j +1 |
i, j |
i, j −1 |
|
+ f it, j |
|
|
h2 |
|
|
||
|
|
|
|
|
|
|
;
,
каждое из которых является неявным по одному направлению и явным по другому. При заданных начальных и граничных условиях последовательно рассчитываются правые части уравнений, после чего производится решение уравнений с использованием прогонки по каждой координате (рис. 4.4).
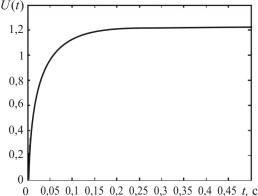
Рис. 4.4. Решение краевой задачи методом переменных направлений ( τ = 0, 001)
Программа решения двумерной краевой задачи с использованием метода переменных направлений:
n1=17; n2=17; h=1./(n1-1); n=1; nk=500; u0(1:n1,1:n2)=0.;(1:n1,1:n2)=0.; f(1:n1,1:n2)=0.; f(8:10,8:10)=100.; f1(1:n1,1:n2)=0.; f2(1:n1,1:n2)=0.; dt=0.001; while n<nk
for i=2:n1-1 for j=2:n2-1
f1(i,j)=(u0(i,j+1)-2.*u0(i,j)+u0(i,j-1))/h^2+2.*u0(i,j)/dt+f(i,j);
end end
100
