
Биомеханика - 2014. Материалы XI Всероссийской конференции с международн
.pdfВсероссийская конференция «БИОМЕХАНИКА – 2014» |
11 |
Results and Discussion
Adaptive gradient elasticity offers a reliable, yet simple model that can be used to simulate stress concentrations in fractured cortical bone. The multi-scale nature of this approach allows capturing the interaction between the microstructure and the macroscopic geometry under given loading conditions.
In analysing the behaviour of the osteoporotic patients, it is of particular importance to correctly simulate the stresses and strains around the tips of sharp cracks. It has already been shown [6] that the gradient elasticity provides a more realistic representation, i.e. removes singularities around the crack tip. In bones of osteoporotic patients the risk of fracture increases as the bones become more porous. Vibration treatment has been shown [1] to be beneficial to the bone by triggering bone formation mechanisms. The adaptive gradient elasticity model offers a tool to account for decrease in the porosity, resulting in an increase of the bone effective stiffness. As a consequence of this, the stresses around the crack tip will also increase. On the other hand, the decrease in the porosity of the bone will result in increasing the strength of the bone. This model removes the un-realistic stress singularities around the crack tip, which results in removal of the un-realistic infinite value of the stress concentration factor.
Acknowledgments
The author gratefully acknowledge financial support of the EPSRC Grant Ref: EP/J004782/1 (“Adaptive Gradient Elasticity and Mechanical Stimulation in Bone Remodelling”).
Reference
1.Mindlin R.D. Micro-structure in linear elasticity // Archive for Rational Mechanics and Analysis. – 1964. – Vol. 16. – Р. 51–78.
2.Mindlin R.D., Eshel N.N. On first strain-gradient theories in linear elasticity // International Journal of Solids and Structures. – 1968. – Vol. 4. – Р. 109–124.
3.Altan B.S., Aifantis E.C. On some aspects in the special theory of gradient elasticity // Journal of the Mechanical Behavior of Materials. – 1997. – Vol. 8. – Р. 231–282.
4.Gitman I.M., Askes H., Aifantis E.C. The Representative Volume size in static and dynamic micromacro transitions // Int. J. Fract. – 2005. – Vol. 135. – Р. L3–L9.
5.Gitman I.M., Askes H., Kuhl E., Aifantis E.C. Stress concentrations in fractured compact bone simulated with a special class of anisotropic gradient elasticity // International Journal of Solids and Structures. – 2010. – No. 47(9). – Р. 1099–1107.
6.Kwong M.T., Gitman I.M. Gradient elastic stress analysis for anisotropic bi-material interface with arbitrary oriented crack // International journal of fracture. – 2012. – Vol. 173. – Р. 79–85.
7.Gitman I.M. Gradient elasticity for modelling periprosthetic fracture at bi-material bone-implant interface // Russian Journal of Biomechanics. – 2010. – Vol. 14, no. 4(50). – Р. 27–35.
8.Rubin C., Recker R., Cullen D., Ryaby J., McCabe J., McLeod K. Prevention of postmenopausal bone loss by a low-magnitude, high-frequency mechanical stimuli: a clinical trial assessing compliance, efficacy, and safety // J. Bone Miner. Res. – 2004. – Vol. 19. – Р. 343–351.
9.Aleyaasin M., Harrigan J.J. Vibration Exercise for Treatment of Osteoporosis: A theoretical Model // Proc. I. Mech. E: Part H: Journal of Engineering in Medicine. – 2008. – No. 222(7). – Р. 1161–1166.
10.Hegedus D.M., Cowin S.C. Bone remodeling II: small strain adaptive elasticity // Journal of Elasticity. – 1976. – Vol. 6. – Р. 337–352.
11.Wolff J. The Law of Bone Remodeling. – Berlin: Heidelberg; New York: Springer, 1986 (translation of the German 1892 edition).
12 |
Всероссийская конференция «БИОМЕХАНИКА – 2014» |
УДК 616.314+616.716.8]-007-089.23
ОПРЕДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ПАРАМЕТРОВ ЗУБОЧЕЛЮСТНЫХ ПРОТЕЗОВ С ТИТАНОВЫМИ КАРКАСАМИ
Н.Б. Асташина, Г.И. Рогожников, С.В. Казаков
Пермская государственная медицинская академия им. акад. Е.А. Вагнера Минздрава России,
Россия, 614000, г. Пермь, ул. Петропавловская, 26, astashina.n @yandex.ru
Ключевые слова: зубочелюстные протезы, сплавы титана, биомеханика.
Введение
Использование зубочелюстных протезов при ортопедическом лечении пациентов с дефектами верхней челюсти может сопровождаться функциональной перегрузкой тканей протезного ложа [1]. Функциональные нагружения развиваются как при откусывании, так и при пережевывании пищи. При этом воспринимаемые жевательные нагрузки передаются через искусственные зубы на каркас протеза, что влечет за собой возникновение зоны прогиба под седлом или базисом конструкции. В указанных участках развивается избыточная нагрузка на подлежащие ткани, что может привести к нарушению кровоснабжения и, как следствие, способствовать развитию атрофических процессов в области протезного ложа.
Материалы и методы
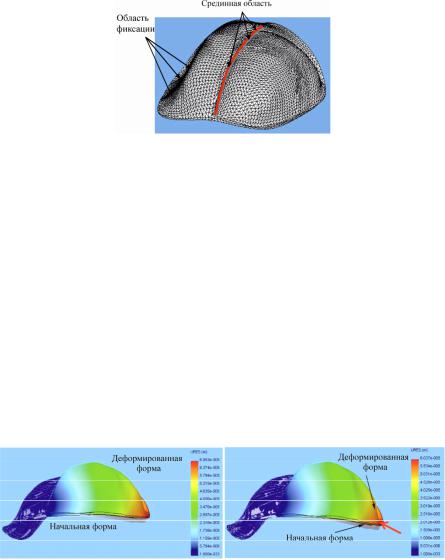
Для ортопедического лечения пациентов с дефектами верхней челюсти разработана конструкция зубочелюстного протеза с полым обтуратором и разнотолщинным титановым каркасом, использование которой позволит устранить функциональную перегрузку тканей протезного ложа. Согласно теории математического моделирования [2] особо следует обосновать, какие компоненты протеза включаются в рассчитываемую модель. Средствами компьютерного моделирования SolidWorks 2006 [3] создавались модели каркаса протеза. Для расчета прогиба по свободному краю протеза определяли зоны фиксации конструкции и величину функциональной нагрузки, приходящейся на протезное ложе. Поверхность протеза, прилегающая к здоровой стороне челюсти, рассматривалась как малоподвижная, а по краю возмещающей части протеза прикладывалась сила, соответствующая суммарному усилию сжатия зубами в 10 кгс. В ходе исследований было выбрано максимально возможное разбиение рассчитываемого объекта на конечные элементы, поскольку протез представляет собой конструкцию, состоящую из оболочек. Изображение набора конечных элементов, на которые разделяется рассчитываемое тело для реализации метода конечных элементов, показано на рис. 1.
Всероссийская конференция «БИОМЕХАНИКА – 2014» |
13 |
Рис. 1. Изображение набора конечных элементов, на которые разделяется рассчитываемое тело для реализации метода конечных элементов
Рассматривались следующие параметры базисов зубочелюстных протезов: для однотолщинной конструкции толщина базиса равномерна и составляет 0,5 мм, а для разнотолщинной – от 0,4 мм в периферической области до 0,6–0,9 мм в области утолщения. Толщина стенки обтуратора у обеих конструкций выбирается одинаковой и равной 0,8 мм. Остальные размеры рассчитываемых протезов одинаковы.
Результаты
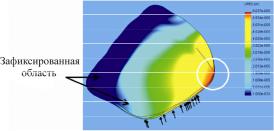
Основные иллюстрации результатов расчетов представлены на рис. 2–4 (серая область иллюстрирует начальную, ненагруженную форму, а цветная – деформированную, «продавленную» форму; цветовая шкала в правой части каждого рисунка показывает, что в красный цвет окрашены области с наибольшим прогибом, синий цвет соответствует минимальному значению). Шкала характеризуется числовыми величинами. Красной стрелкой показаны области, в которых возникает наибольшее давление.
а |
б |
Рис. 2. Иллюстрации прогибов однотолщинной (а) и разнотолщинной (б) конструкций: жирной стрелкой показаны зоны наибольшего прогиба
Проведенный биомеханический анализ результатов исследований показал, что при функциональной нагрузке зафиксированная часть каркаса оста-
14 |
Всероссийская конференция «БИОМЕХАНИКА – 2014» |
ется малоподвижной и именно в этой зоне возникают незначительные напряжения. Срединная часть конструкции опирается на костную ткань твердого нёба, и прогиб здесь также минимален, однако в этой области наблюдается значительное давление, переданное от жевательной нагрузки конструкцией через каркас конструкции и обтуратор. В пластине обтуратора и свободной от фиксирующих элементов части каркаса не образуется существенных напряжений. Но именно на участках протезного ложа, лежащих под указанными конструкционными элементами, создается наиболее значимое продавливание мягких тканей. На рис. 2 показано сравнение прогибов однотолщинной и разнотолщинной конструкций. Сопоставление иллюстраций (рис. 2, а, б) показывает, что наибольшее значение прогиба однотолщинной конструкции равно 6,953·10–2 мм (см. рис. 2, а), а разнотолщинной – 6,037·10–2 мм (см. рис. 2, б). На этом рисунке и далее обозначение 6.953е-005 соответствует 6,935·10–2 мм. Функциональная нагрузка, воздействующая на протез (см. рис. 3), продавливает каркас в указанной зоне, вызывая наибольший прогиб. Зона наибольшего продавливания при использовании разнотолщинной конструкции показана на рис. 3.
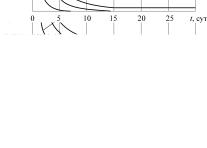
Рис. 3. Иллюстрация прогиба каркаса разнотолщинной конструкции (кругом показана область, в которой возникает наибольшее продавливание, на цветовой шкале справа указаны соответствия перемещения и цвета: вертикальные стрелки указывают направление жевательной нагрузки)
Сравнение величины продавливания каркасов однотолщинной и разнотолщинной зубочелюстных конструкций представлено на диаграмме (см. рис. 4). На рис. 4, а изображена кривая АВС, проходящая вдоль свободного края каркаса конструкции. На рис. 4, б изображен уровень прогиба вдоль кривой АВС. Видно, что наибольшее продавливание возникает в зоне В.
Обсуждение
Таким образом, рациональным является моделирование базиса или каркаса конструкции с утолщением края в зоне наибольшего продавливания, т.е. по свободному краю конструкции, прилегающему к области дефекта челюсти. При использовании разнотолщинного каркаса зубочелюстного проте-

Всероссийская конференция «БИОМЕХАНИКА – 2014» |
15 |
за верхней челюсти уменьшается продавливание слизистой оболочки протезного ложа вдоль свободного края конструкции на величины, находящиеся в пределах от 10,18 до 15,1 %.
а
б
Рис. 4. Иллюстрация разницы величины продавливания у однотолщинного и разнотолщинного каркаса: а – продавливание показано для точек кромки АВС; б – на диаграмме по горизонтальной оси откладывается положение точек вдоль кривой АВС, а по вертикальной оси – соответствующее продавливание
Особенно значительный эффект возникает в зоне наибольшего прогиба (вдоль зоны В кривой на рис. 4, а). Рассчитанный эффект получен для конструкции, которая по своим весовым и объемным характеристикам близка к традиционной на уровне допустимой погрешности. Следовательно, уменьшение уровня продавливания достигается за счет рационального конструирования зубочелюстного протеза.
Список литературы
1.Жулёв Е.Н. Арутюнов С.Д., Лебеденко И.Ю. Челюстно-лицевая ортопедическая стоматоло-
гия. – М.: МИА, 2008. – 160 с.
2.Введение в математическое моделирование: учеб. пособие / под ред. П.В. Трусова. – М.: Ло-
гос, 2004.
3.Алямовский, А.А. SolidWorks/COSMOSWorks. Инженерный анализ методом конечных элементов. – М.: ДМК Пресс, 2004.
16 |
Всероссийская конференция «БИОМЕХАНИКА – 2014» |
УДК 519.216-047.58
БИОМЕХАНИЧЕСКИЕ ОСНОВЫ ПРОЦЕССА БИОЛОГИЧЕСКОЙ ДЕСТРУКЦИИ ЛЕКАРСТВЕННЫХ СРЕДСТВ С ПРИМЕНЕНИЕМ АКТИНОБАКТЕРИЙ
А.А. Баранова1, Е.В. Вихарева2, А.А. Селянинов1
1Пермский национальный исследовательский политехнический университет,
Россия, 614990, г. Пермь, Комсомольский пр., 29, aabaranova20@gmail.com
2Пермская государственная фармацевтическая академия, России, г. Пермь, ул. Полевая, 2
Ключевые слова: лекарственные средства, биологическая деструкция, биомеханические основы, кинетика, нестационарный процесс, стохастический анализ.
Введение
Биологическая деструкция лекарственных средств является экологически чистым процессом, который в менее интенсивном режиме проходит в природных условиях. При этом интерес представляет уменьшение концентрации лекарственного средства со временем. Сам процесс связан с подачей лекарственного средства из культуральной жидкости к колониям актинобактерий, адсорбированных на носителях (типа опилок).
Материалы и методы
В лабораторных условиях колбы с культуральной жидкостью помещаются в шейкер. Стенки колб совершают поступательное движение по окружности, а культуральная жидкость при этом перемешивается. Из-за неравномерности движения культуральная жидкость с актинобактериями на носителе совершает поступательное движение с центром масс и вращательное относительно центра масс, в результате чего колонии актинобактерий получают свежие порции культуральной жидкости с лекарственным средством и питательной средой. При этом интенсивность перемешивания считается равномерной по объему и характеризуется угловой скоростью привода плиты шейкера. От угловой скорости привода зависит скорость процесса биологической деструкции, которая характеризуется уменьшением концентрации лекарственного средства во времени.
Различают интенсивный и экстенсивный процессы. Интенсивный характеризуется максимальной скоростью уменьшения концентрации в начальный момент времени с последующим убыванием, а экстенсивный – медленно нарастающей скоростью в начале процесса, затем достижением ее максимальной величины с последующим уменьшением. Изменение концентрации в качестве определяющего параметра описывается кинетическим уравнением первого порядка с различными параметрами в зависимости от интенсивности процесса:
Всероссийская конференция «БИОМЕХАНИКА – 2014» |
17 |
|
dx |
= −K (t) x, |
(1) |
dt |
|
|
где так называемая константа реакции K может быть функцией времени. Важным моментом лабораторного исследования является повторяе-
мость биологической деструкции (таблица), которая необходима для валидации (аттестации) этого процесса. Процесс оказался нестационарным случайным, так как при фиксированных условиях новые реализации отличаются от предыдущих.
Изменение содержания дротаверина гидрохлорида в процессе биологической деструкции, %
Время t, сут |
x1 |
x2 |
x3 |
0 |
100 |
100 |
100 |
2 |
40,50 |
7,30 |
– |
5 |
27,90 |
3,75 |
10,20 |
20 |
9,10 |
2,80 |
– |
30 |
1,2 |
0,7 |
0,9 |
Особенность данного процесса состоит в отсутствии некоторых экспериментальных данных на определенный момент времени.
На рис. 1 приведены реализации процесса биологической деструкции с одним параметром k в кинетическом уравнении.
Рис. 1. Реализации случайного процесса биологической деструкции при экспериментах на повторяемость после кинетического моделирования: 1, 2, 3 – номера экспериментов
Как следует из рис. 1, кинетические кривые достаточно адекватно описывают уменьшение концентрации при биологической деструкции дротаверина гидрохлорида.
Результаты
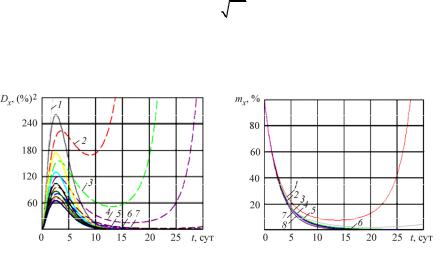
В работе произведен стохастический анализ этого процесса двумя приближенными методами: линеаризации и полного анализа при гипотезе о нормальном законе распределения случайной величины. Получена сходимость этих подходов (рис. 2), которая определила ограничения на дисперсии параметров кинетического уравнения:
18 |
Всероссийская конференция «БИОМЕХАНИКА – 2014» |
||||
|
t << |
1 |
|
, |
(2) |
|
|
|
|||
|
D |
|
|||
|
|
|
k |
|
|
где Dk – дисперсия случайной величины k.
Для вывода аналитических выражений числовых характеристик случайного процесса была доказана и применена Лемма.
a |
б |
Рис. 2. Сходимость: a – дисперсии Dx(t); б – математического ожидания процесса mx(t) при уменьшении дисперсии Dk; 1 – при исходных данных; 2 – Dk/1,5; 3 – Dk/2; 4 – Dk/2,5; 5 – Dk/3;
6 – Dk/3,5; 7 – Dk/4
Обсуждение
Математические ожидания сходятся при Dk/2, а дисперсии при Dk/4 (практически при Dk/3), т.е. ограничения на дисперсии случайной величины заметно более жесткие для дисперсии случайного процесса, нежели математического ожидания случайного процесса. Эти результаты отражают выражения по ограничению на дисперсии (тоже разница в 2 раза).
Благодарности
Благодарим профессора И.Б. Ившину за предоставление результатов эксперимента по биологической деструкции и профессора Ю.И. Няшина за обсуждение результатов кинетического и стохастического моделирования биологической деструкции лекарственных средств.
Список литературы
1.Селянинов А.А. Класс кинетически моделируемых биомеханических случайных процессов // Российский журнал биомеханики. – 2012. – Т. 16, № 4. – С. 22–35.
2.Селянинов А.А., Вихарева Е.В. Кинетика биодеструкции лекарственных средств – производных фенола, изохинолина и карбоновых кислот // Российский журнал биомехани-
ки. – 2010. – Т. 14, № 3. – С. 79–91.
3.Селянинов А.А., Вихарева Е.В., Ившина И.Б., Баранова А.А., Карпенко Ю.Н. Стохастический анализ повторяемости процесса биодеструкции дротаверина гидрохлорида // Российский журнал биомеханики. – 2013. – Т. 17, № 1(59). – С. 41–54.
Всероссийская конференция «БИОМЕХАНИКА – 2014» |
19 |
УДК 532.29
АСИМПТОТИКА И ЧИСЛЕННЫЙ РАСЧЕТ СПИРАЛЬНЫХ ВОЛН В АОРТЕ
В.А. Батищев, Д.С. Петровская
Южный федеральный университет,
Россия, 344090, г. Ростов-на-Дону, ул. Мильчакова, 8а, batishev-v@mail.ru
Ключевые слова: аорта, оболочка, спиральные волны, асимптотика, расчет.
Введение
Во второй половине прошлого века началось активное изучение винтовых течений крови в кровеносных сосудах человека и животных. Однако еще
вXVII в. W. Harvey наблюдал закрученное движение крови в сердце. Анализ экспериментальных данных показал, что спиральное течение крови возникает в левом желудочке сердца в диастолу и усиливается в систолу. Закрученный поток крови поступает из сердца в аорту и вызывает длинные и короткие спиральные волны. К причинам возникновения спиральных течений крови
ваорте относятся и механические свойства стенок кровеносных сосудов. В работе [1] Ю.А. Устинов построил математическую модель длинных спиральных пульсовых волн в артериальных сосудах с учетом винтовой анизотропии стенок сосудов.
Внастоящей работе исследованы короткие спиральные волны. Показано, что в аорте возможны различные режимы вращательного движения жидкости. В течение систолы направление вращения может измениться на противоположное как один, так и несколько раз. Наибольшего значения окружная компонента скорости достигает во второй половине систолы.
Асимптотические решения спиральных волн
Рассматривается задача о спиральных волнах малой амплитуды в аорте, которая моделируется цилиндром кругового сечения. Поверхность цилиндра представляет собой тонкую упругую изотропную оболочку толщиной h и радиусом срединной поверхности а. Движение жидкости рассчитывается на основе системы уравнений Навье – Стокса.
Исследуется осесимметричная задача в цилиндрических координатах, причем вектор скорости, давление и смещения точек срединной поверхности оболочки не зависят от окружной координаты θ. Течение жидкости периодично по времени с заданным периодом Т. Приведем уравнение для окружной компоненты вектора скорости [2]:
∂vθ + R |
v |
∂vθ + v |
|
∂vθ + vr vθ |
= ε2 |
|
2v − |
vθ |
. |
||||
z |
|
|
|||||||||||
∂t |
|
r |
∂r |
∂z |
r |
|
ν |
θ |
r |
2 |
|
||
|
|
|
|
|
|
|
|
|
|||||
20 |
Всероссийская конференция «БИОМЕХАНИКА – 2014» |
Здесь |
R = U /(aω) , где U – максимальное значение скорости частиц |
жидкости в поле длинных продольных волн; ω= 2π/T. Параметр εν мал.
В работе используются динамические уравнения тонкой упругой цилиндрической оболочки, моделирующей стенки аорты. В безразмерных переменных в уравнениях оболочки возникает малый параметр εk .
Решение задачи представим в |
виде суммы трех вектор-функций: |
V = V0 (r, z) + V1(r, z1,t) + V2 (r, z, z1,t). |
Здесь z1 – медленная осевая коорди- |
ната, z1 = εk z. Вектор V0 – описывает стационарное течение Пуазейля
вкруговом цилиндре со скоростью V(r). Векторы V1 = (vr ,vθ,vz , p,ur ,uθ,uz )
иV2 = (wr ,wθ, wz ,q,u1r ,u1θ,u1z ) описывают соответственно длинные и корот-
кие волны. Первые четыре компоненты векторов V0 ,V1,V2 – это компонен-
ты вектора скорости и давление, а последние три – это компоненты смещений точек срединной поверхности оболочки. Отметим, что длинные спиральные волны локализованы в пограничном слое вблизи оболочки.
В отличие от длинных спиральных волн короткие спиральные волны заполняют всё поперечное сечение цилиндра. Эти волны описываются окружной компонентой wθ вектора V2. Предположим, что компонента wθ
имеет такой же порядок малости O(εk ), как и окружная длинноволновая компонента vθ. Покажем, что короткие спиральные волны слабо зависят от
упругих свойств оболочки, а механизмом их переноса является стационарный поток. Асимптотические разложения компонент вектора V2 при εk → 0
представим в виде
w = ε |
w |
+..., w = ε2 w |
+..., |
u1 |
= ε3u |
θ1 |
+.... |
θ |
k θ1 |
z k z1 |
|
θ |
k |
|
Остальные компоненты разлагаются в аналогичные ряды. Компонента wθ1 учитывает конвективный перенос как средним потоком, так и длинными
волнами и определяется из краевой задачи
|
∂wθ1 + RV |
∂wθ1 = ε2 |
2w |
− |
wθ1 |
, |
|
||||
|
|
|
|||||||||
|
∂t |
z |
∂z |
ν |
|
θ1 |
|
r |
2 |
|
(1) |
|
|
|
|
|
|
|
|
||||
wθ1 = 0 |
(r = 1), wθ1 = 0 (r = 0), wθ1 → 0 (z → ∞). |
|
|||||||||
Здесь Vz – главный член асимптотики компоненты vz вектора V1 |
при |
||||||||||
εk → 0, Vz = vz0 (r, |
z1, t )+V (r). Функцию |
vz0 |
представим в виде суммы |
||||||||
двух слагаемых vz0 =vz00 (t, z1 )+hz0 (t, z1, s1 ), |
где vz00 |
определена во всей об- |
|||||||||
ласти течения, а функция hz0 |
локализована в пограничном слое вблизи обо- |
||||||||||
лочки. |
|
|
|
|
|
|
|
|
|
|
|
