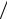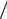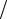ym = {[(h −1)2 +1]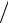 2}m .
2}m .
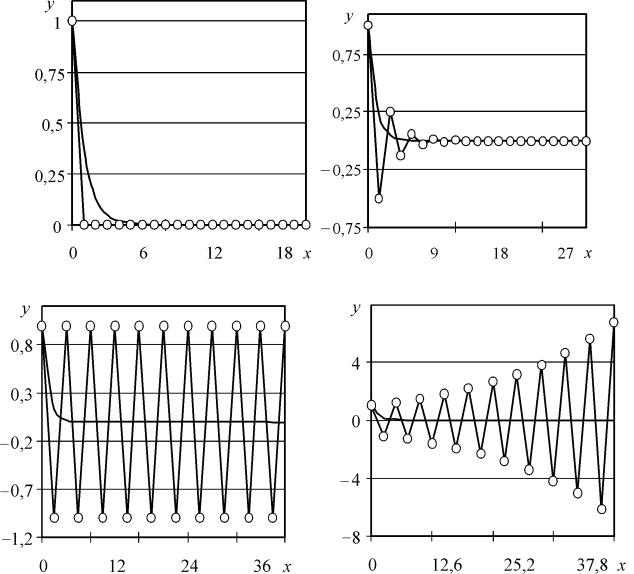
Рзультаты получаемого численного решения для значения аргумента x = 10 при различных шагах интегрирования приведены в табл. 8.2. Три верные значащие цифры получены теперь для шага h = 0,01.
Таблица 8.2 Результаты численного решения ym методом Рунге–Кутты второго порядка
дифференциального уравнения y′ = −y с начальным условием y(0) =1
Величина шага h |
0,5 |
0,25 |
0,1 |
0,01 |
0,001 |
0,0001 |
|
|
|
|
|
|
|
Число шагов m |
20 |
40 |
100 |
1000 |
10000 |
100000 |
|
|
|
|
|
|
|
ym104 |
0,827181 |
0,514756 |
0,462229 |
0,454076 |
0,454000 |
0,453999 |
Для оценки погрешности аппроксимации уравнения (8.1) разностной схемой метода Рунге–Кутты точное решение подставляется в разностный аналог исходного дифференциального уравнения и вычисляется невязка:
ψk = [y(xk +1 )− y(xk )]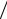 h − (1 − α)f (xk , y(xk ))−
h − (1 − α)f (xk , y(xk ))−
−αf (xk + h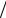 2α, y(xk )+ hf (xk , y(xk ))
2α, y(xk )+ hf (xk , y(xk ))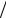 2α).
2α).
Разложения функций в ряды Тейлора
y(xk+1 )= y(xk )+ y′(xk )h + y′′(xk )h2 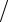 2 + O(h3 ),
2 + O(h3 ),
f(xk + h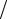 2α, y(xk ) + hf (xk , y(xk ))
2α, y(xk ) + hf (xk , y(xk ))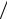 2α)=
2α)=
=f (xk , y(xk ))+ hfx′(xk , y(xk ))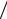 2α + O(h2 )
2α + O(h2 )
подставляются в полученное выражение:
ψk = [y(xk ) + y′x (xk )h + y′xx′ (xk )h2 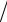 2 +O(h3 )− y(xk )]
2 +O(h3 )− y(xk )] h − (1 − α)f (xk , y(xk ))−
h − (1 − α)f (xk , y(xk ))−
−α{f (xk , y(xk ))+ hfx′(xk , y(xk )) 2α + O(h2 )}=
2α + O(h2 )}=
=y′(xk )− f (xk , y(xk ))+h[y′′(xk )− fx′(xk , y(xk ))] 2 +O(h2 ).
2 +O(h2 ).
Учитывая уравнение (8.1), а также выражение для производной,
y′′(xk ) = [y′(xk )]′ = f x′(xk , y(xk )),
можно получить, что ψk = O(h2 ), то есть метод Рунге–Кутты, независимо от значения параметра α имеет погрешность аппроксимации второго порядка.




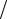 h
h 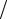

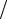

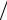 2 =
2 = 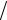 2 ,
2 , 2.
2.
 2.
2. 2 ,
2 ,

 2
2 2 ,
2 ,  2
2  2
2 2
2  2
2
 h
h 




 24
24 24
24 24
24 24
24 24
24 24
24 24]
24]
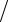 4 .
4 .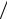 12
12