Сопротивление материалов курс лекций

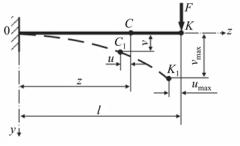
Лекция 10

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ

Для того чтобы судить о работоспособности конструкций, испытывающих изгиб, знать возникающие в сечениях напряжения часто бывает недостаточно. Балки могут удовлетворять условиям прочности, но при этом быть непригодными к эксплуатации из-за недостаточной жёсткости. Для проверки условий жёсткости необходимо уметь определять перемещения точек оси балки.

Ограничимся пока рассмотрением плоского изгиба, когда действующие на балку силы лежат в плоскости, проходящей через ось симметрии поперечного сечения.

Рис. 10.1.

Под действием приложенной нагрузки произвольная точка С оси балки, отстоящая от начала координат на расстоянии z, переместится в новое положение С1 (рис. 10.1). Обозначим её вертикальное перемещение величиной v, горизонтальное – u. Проверка жёсткости балки сводится к условию, по которому наибольший прогиб vmax не должен превышать некоторой заданной доли от продольного размера конструкции – длины пролёта, либо длины консольного участка, в зависимости от условий закрепления балки:

Величина m устанавливается нормами проектирования и обычно лежит в пределах 200...1000 единиц. Отсюда следует, что перемещения при изгибе малы по сравнению с размерами конструкции. Этот факт позволяет ввести некоторые упрощения, в частности пренебречь горизонтальными перемещениями u. В дальнейшем будем учитывать только вертикальные перемещения v (в общем случае – перемещения, нормальные к недеформированной оси), называя их

прогибами балки (рис. 10.2)

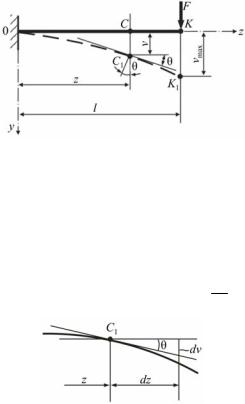
Рис. 10.2.

В точке С1 к оси изогнутой балки проведена касательная, угол наклона которой к оси z обозначен θ. Принимая гипотезу плоских сечений, можно считать, что угол поворота поперечного сечения в этой точке также равен θ (см. рис. 10.2)

Бесконечно малому приращению координаты dz соответствует приращение прогиба dv (рис. 10.3), откуда tgθ= dvdz .

Рис. 10.3.

При малых прогибах малы и углы θ, вследствие чего можно считать tg θ ≈ θ, где угол выражен в радианах.

132

Окончательная связь между прогибами v и углами поворота сечения θ принимает вид

Таким образом, задача определения перемещений при изгибе сводится к отысканию двух функций – прогибов v (z) и углов поворота θ (z).

Введём для них следующие правила знаков:

•прогиб будем считать положительным, если он направлен в сторону координатной оси у;

•угол поворота положителен, если касательная поворачивается по кратчайшему пути от направления оси z к направлению оси у.

Рис. 10.4.

На рис. 10.2 и прогиб, и угол поворота положительны. При других направлениях координатных осей для правильного выбора знака θ можно пользоваться схемой, показанной на рис. 10.4.

Дифференциальное уравнение изогнутой оси балки

При рассмотрении нормальных напряжений при изгибе нами была получена связь между кривизной балки ρ1 и изгибающим мо-

ментом в сечении:

1= M x .

ρEIx

133

С другой стороны, из курса высшей математики известно выражение для кривизны плоской кривой, описываемой уравнением v(z):

Приравнивая правые части этих выражений, будем иметь

Полученное уравнение называют точным уравнением изогнутой оси балки. Нелинейность этого дифференциального уравнения вызывает значительные трудности при интегрировании. Однако для большинства решаемых практических задач справедливы предположения о малости прогибов и углов, что позволяет исключить нелинейность в (10.4), поскольку стоящая в знаменателе формулы производная

dvdz =θ<<1,

и квадратом этой величины по сравнению с единицей можно пренебречь.

Полученное таким образом упрощенное линейное уравнение

мы в дальнейшем будем называть дифференциальным уравнением изогнутой оси балки. Знак в правой части уравнений (10.3)–(10.5) определяется направлением вертикальной оси у. При положитель-

134

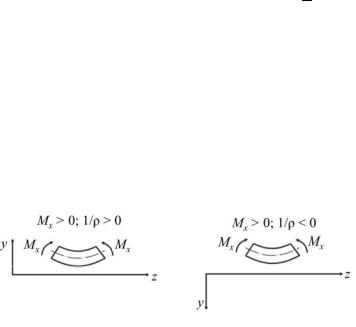
ном значении изгибающего момента ось балки имеет характер вогнутой кривой с центром кривизны, расположенным в верхней по-

луплоскости. Если ось y направлена вверх, кривизна ρ1 оказывается

положительной (рис. 10.5, а), и правую часть необходимо брать со знаком плюс:

в противном случае, когда ось у направлена вниз, в правой части уравнения должен стоять минус (см. рис. 10.5, б):

Рис. 10.5.

Как говорилось ранее, в большинстве случаев мы будем направлять ось у вниз и использовать дифференциальное уравнение оси балки в форме (10.7).

Определение перемещений непосредственным интегрированием уравнения изогнутой оси балки

Для нахождения аналитических выражений прогибов и углов поворота необходимо решить дифференциальное уравнение (10.7). Эта задача упрощается в случае, если жёсткость балки остаётся постоянной по всей длине (EIx = const).

135

Зная закон изменения изгибающих моментов по длине балки, можно считать правую часть уравнения (10.8) известной. Проинтегрируем левую и правую части уравнения:

∫EIx ddz2v2 dz =−∫M x dz .

Порядок производной в левой части уравнения понизится, в результате чего будем иметь выражение для углов поворота, как функции координаты z.

EIx dvdz =EIxθ=−∫M x dz +C1 .

Повторное интегрирование даёт выражение для функции прогибов

EIxv =−∫dz∫M x dz +C1z +C2 .

Здесь С1, С2 – постоянные интегрирования, которые могут быть найдены из условий закрепления балки.

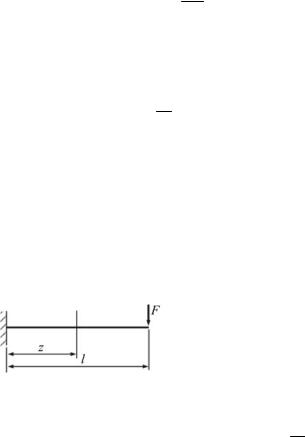
Пример 10.1. Нахождение углов поворота и прогибов консольной балки.

Решение. Запишем выражение для изгибающих моментов Мх в произвольном сечении балки z:

M x =−F (l −z).

Уравнения для углов поворота и прогибов примут вид:

EIxθ=∫F (l −z)dz +C1 =Flz −F z22 +C1 ,

136

Постоянные интегрирования найдём из граничных условий:

при z = 0: v = 0; θ = 0;

откуда следует

С1 = 0; С2 = 0.

Таким образом, получаем окончательный вид для функций пе-

Для шарнирно опёртой балки граничными условиями служат равенства нулю прогибов над опорами. В тех случаях, когда на разных участках балки изгибающий момент имеет различные законы изменения, для каждого такого участка необходимо составлять свои дифференциальные уравнения. При их интегрировании появляются дополнительные постоянные, общее число которых равно удвоенному числу участков. Для определения постоянных интегрирования помимо условий закрепления необходимо использовать условия непрерывности решений на границах участков:

θЛ =θП; vЛ =vП,

где индекс «л» соответствует значению перемещений при подходе к границе участков слева, а «п» – справа.

Появление дополнительных постоянных интегрирования может значительно усложнить задачу, поэтому изложенный подход используется лишь в простейших случаях, когда мы имеем дело с одним, в крайнем случае – с двумя силовыми участками.

137

Определение перемещений в балках методом начальных параметров

Данный метод был разработан с целью упрощения расчётов при нахождении функций прогибов и углов поворота в балках. Его суть заключается в использовании универсальных уравнений для функций перемещений, содержащих только две постоянные интегрирования, независимо от числа силовых участков. Эти константы представляют собой значения угла поворота и прогиба в начале координат (начальные параметры) и легко находятся из условий закрепления балки.

Рассмотрим участок балки длиной z, нагруженный, как показано на рис. 10.6.

Рис. 10.6.

Начало координат выбрано на левом торце балки, ось ординат у направлена вниз, направление нагрузок таково, чтобы создаваемый ими в сечении z изгибающий момент был отрицательным.

Запишем уравнение изогнутой оси в форме

EIx ddzθ=−M x

и проинтегрируем его от 0 до z:

z

EIxθ 0z =−∫M x dz .

0

138

Полученный результат представим в следующем виде:

Прогиб и угол поворота в начале координат, входящие в правую часть выражения (10.10), называют начальными параметрами и обычно обозначают следующим образом:

EIxv0 =EIxv(0), (10.11)

EIxθ0 =EIxθ(0).

Рассмотрим подробнее интеграл, входящий в правую часть уравнения (10.9). Для этого представим изгибающий момент в виде суперпозиции моментов от каждой из нагрузок в отдельности:

∫z M x (z)dz =−∫z (M xM +M xF +M xq )dz =

В нижних пределах интегрирования учтено, что нагрузки создают изгибающий момент на участке, лишь начиная с некоторого значения координаты z: момент М – начиная со значения z = а, силы F – с точки её приложения z = b и т.д.

139

Интегрируя по известным правилам без раскрытия скобок, получим:

Повторное интегрирование даёт следующий результат:

Подставляя полученные выражения в (10.9), (10.10), найдём уравнения для углов поворота и прогибов:

Обобщая результат на случай произвольного числа внешних нагрузок, получим универсальные уравнения метода начальных параметров для перемещений при изгибе:

Здесь θ0, v0 – угол поворота и прогиб балки в начале координат (начальные параметры), определяемые из граничных условий;

Mi, Fj, qk – действующие на балку нагрузки;

l, m, n – количество соответствующих нагрузок, приложенных на участке балки от начала координат до сечения z;

140