Оптимальное проектирование конструкций

S1(t) представляет собой некоторую гиперповерхность или кривую в Rn, то левый (правый) конец называют подвижным.

В задаче (5.11)–(5.14) моменты времени t0 и Т в общем случае могут быть неизвестны, тогда они будут зависеть от управления и их необходимо определить. В частности, если f0 ≡ 1, F (x) ≡ 0 , то I (u) ≡ Т − t0 , и задачу

(5.11)–(5.14) называют задачей быстродействия. Если же моменты t0 и Т известны, то задачу называют задачей оптимального управления с закрепленным временем.

Наряду со сформулированной выше задачей в теории оптимального управления рассматриваются задачи с запаздыванием, с параметрами, с изопериметрическими условиями, с дискретным временем и т.д.

В заключение отметим, что именно наличие замкнутого множества U отличает постановку оптимального управления от вариационной форму-

лировки. Как известно, если U = Rn , то задача (5.11)–(5.14) называется задачей Больца, если в (5.11) F (х(Т),Т) = 0 , то имеем задачу Лагранжа, а ес-

ли интеграл в (5.11) равен нулю, то такую задачу называют задачей Майера.

5.2.2. Необходимые условия оптимальности

(принцип максимума)

Рассмотрим задачу оптимального управления (5.11)–(5.14) для случая, когда моменты t0 и Т закреплены. Для формулировки принципа максимума наряду с системой (5.12) рассмотрим следующую систему линейных дифференциальных уравнений относительно вспомогательных (до-

любых начальных условиях и любой заданной ψ 0 . Систему (5.15) называ-

ют сопряженной системой.

Составим функцию Гамильтона – Понтрягина:

n

H (x, ψ , ψ 0 , u, t) = ∑ ψ i fi (x, u, t) ,

i =0

где ψ 0 (t) ≡ ψ 0 – некоторая постоянная.

141

Системы (5.12) и (5.15) можно записать в симметричном виде:

ся функцией лишь параметра u U и можно найти ее максимальное значение. Поэтому теорему о необходимом условии оптимальности называют принципом максимума.

Теорема. Пусть x* (t), u* (t), t0 ≤ t ≤ Т – оптимальное решение задачи (5.11)–(5.14) (t0 и Т заданы). Тогда существуют непрерывная вектор-

полнены условия трансверсальности на левом и правом концах.

Поясним условие трансверсальности для случая различных режимов на правом конце траектории:

а) если правый конец свободен, то из условия трансверсальности

( ψ 1(Т) х1(Т) + ... + ψ n (Т) хn (Т) = 0) следует, что ψ * (Т) = 0;

б) если правый конец подвижен, то условие гарантирует существование таких постоянных а1, а2 , ..., аn , при которых

где h j – функции, характеризующие кривые, по которым перемещается ко-

нец.

Аналогичные соотношения можно записать для левого конца.

142

Доказательства принципа максимума можно найти в [15] и др. Там же показано, что условие (5.16) можно представить в виде

где t – некоторый подходящим образом выбранный момент времени. Если заранее известно, что ψ 0 < 0 , то можно принять ψ 0 = −1.

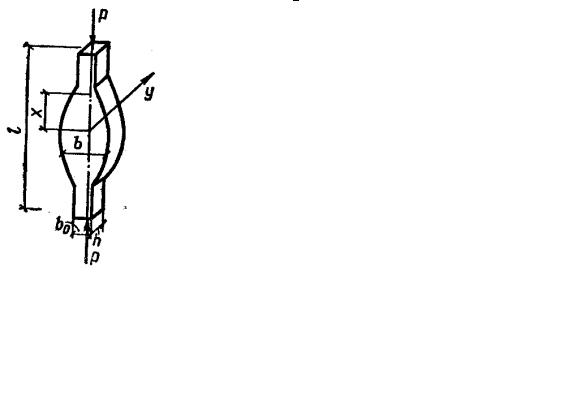
Пример 5.3. Оптимальное проектирование стойки [13]. Сжатая шарнирно-опертая стойка длиной l имеет прямоугольное поперечное сечение постоянной толщины h и переменной ширины b. Определить закон изменения ширины b, чтобы объем стойки был минимальным при условии, что устойчивость теряется в направлении h, а ширина b ограничена снизу: b ≥ b0 (рис. 5.6).

Р е ш е н и е . Из соображений симметрии можно в качестве целевой функции взять объем половины стойки, тогда необходимо найти такое b(x) ,

чтобы

Чтобы решить задачу с помощью принципа Л.С. Понтрягина, перепишем дифференциальное уравнение второго порядка (5.20) в виде системы двух уравнений первого порядка:

где y1 = y; y2 = y′. Тогда граничные условия (5.21) примут вид

143

Система уравнений (5.23) имеет те же коэффициенты и граничные условия, что и система (5.26) и, следовательно, такое же (в силу однородности – с точностью до постоянного множителя) решение

ψ 1 = −Су2 ; ψ 2 = Су1. (5.28)

Если в гамильтониане (5.25) положить ψ 0 = 0 , то Н достигнет своего

максимума при b = 0 , что противоречит физическому смыслу задачи, следовательно, ψ 0 < 0 и можно считать, что ψ 0 = −1, и с учетом (5.28) гамиль-

тониан можно записать в виде

Так как устойчивость теряется по первой форме, что соответствует монотонно убывающей на [0, l / 2] функции, то b(x) не может иметь более од-

144

Рассмотрим решение на каждом из интервалов отдельно:

а) если x1 ≤ x ≤ l / 2 , то b = b0 и решением системы (5.23) с учетом граничного условия y1(l / 2) = 0 будет функция

Таким образом, сжатая стойка минимального веса имеет прямолинейный участок шириной b = b0 и участок, очерченный по параболе, ши-

рина которого

b = b0 + 6P3 (x12 − x2 ). Eh

145

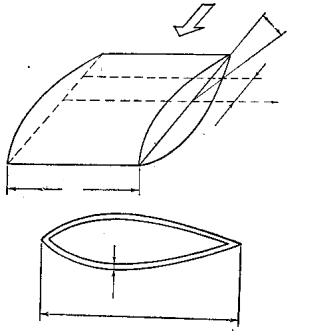
Пример 5.3. Проектирование прямоугольного крыла минимальной массы при заданной скорости дивергенции [1]. Рассмотрим консольное прямое крыло с упругой осью, перпендикулярной набегающему потоку. Предполагается, что профиль крыла не изменяется вдоль оси и характери-

зуется коэффициентом подъемной силы а0. Остальные параметры и обозначения приведены на рис. 5.7. Толщина T обшивки профиля переменна вдоль оси.

v

b

L

Т0

с

Рис. 5.7

Постановка этой задачи была дана в примере 1.5, поэтому запишем без пояснений математическую постановку задачи: найти распределение толщины крыла t(x) , минимизирующее массу крыла:

146

и граничных условиях

где х и t(х) – безразмерные параметры

x = X , t = T , 0 ≤ x ≤ 1. L T0

Для решения задачи введем новую переменную s = t dθ , тогда урав- dx

нение (5.32) запишется в виде системы двух уравнений первого порядка:

Система уравнений (5.34) имеет те же коэффициенты и граничные условия, что и система (5.37) и, следовательно, такое же (в силу однородности – с точностью до постоянного множителя) решение:

ψ 1 = −Су2 ; ψ 2 = Су1. (5.39)

Если в гамильтониане (5.36) положить ψ 0 = 0 , то Н достигнет своего

максимума при t = 0 , что противоречит физическому смыслу задачи, следовательно, ψ 0 < 0 и можно считать, что ψ 0 = −1, и, с учетом (5.39), га-

мильтониан можно записать в виде

147

Если на толщину не наложено никаких ограничений, то из условия максимума (5.40) имеем

тому, как это было сделано в предыдущем примере:

t = tmin + ω 2 (x1 − x) ,

4

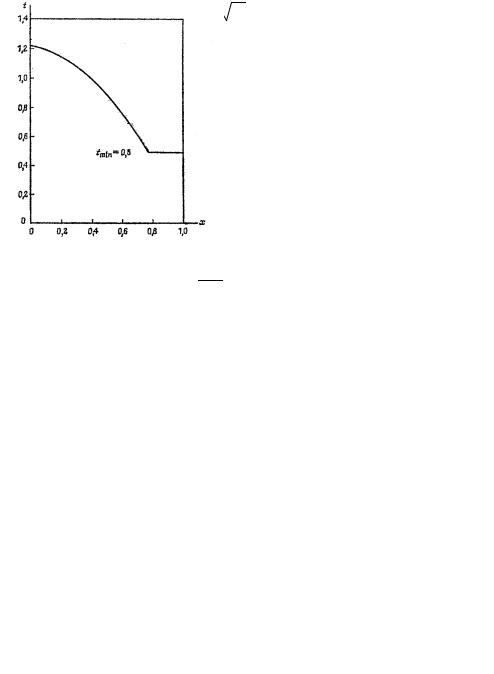
где х1 находим из условия сопряжения решений. На рис. 5.8, а, б приведе-

ны решения для рассмотренных двух вариантов (а – распределение толщины обшивки при отсутствии ограничений на параметр; б –наличии ограничения и tmin = 0,5 ).

Рис. 5.8

148

5.3. Анализ чувствительности для случая оптимального проектирования систем при статических нагрузках

Как указывалось ранее, основная задача анализа чувствительности заключается в установлении эффективных соотношений между изменениями в проектах конструкции и в их функциональных характеристиках

Рассмотрим нахождение вектора чувствительности при решении задач статики методом конечного элемента. Тогда ограничения (4.29), т.е. уравнения равновесия в перемещениях, можно для упругой задачи записать в виде

u – вектор узловых перемещений.

Приведенная матрица жесткости положительно определена, следовательно, невырожденная. В данном случае понятие приведенная подразумевает учет граничных условий.

Используя правило дифференцирования сложной функции и обозначения матричного исчисления, можно вычислить полную производную

Здесь и далее значком ~ обозначаем переменную, которая в процессе частного дифференцирования должна быть постоянной.

Так как K (х) невырожденная, то с учетом (5.44)

Подставив (5.45) в (5.43), получим

149

Как и прежде, чтобы избежать обращения матрицы жесткости, можно использовать два метода: прямой метод дифференцирования: численно решить (5.44) и результат подставить в (5.44), и метод сопряженных переменных, для чего введем сопряженную переменную λ :

Обратим внимание, что уравнение (5.48) совпадает по форме с (5.45), поэтому определение сопряженной переменной не требует дополнительных программных продуктов. Вычисление же производной от матрицы жесткости по переменной проектирования может быть выполнено либо численным дифференцированием, например, на основе конечноразностного приближения, либо непосредственным дифференцированием выражений.

Подобные соотношения могут быть получены, например, для случая ограничений на собственные значения, а также при решении задач динамики или варьировании границы области исследования.

Вектор чувствительности, кроме того, может быть полезен в известных алгоритмах оптимизации, использующих первые производные. Это градиентные методы, а так как решаемая задача есть задача с ограничениями, то в первую очередь это относится к методу проекции градиента.

Метод проекции градиента в пространстве состояний

В методе проекции градиента сначала определяется направление, вдоль которого происходит наиболее быстрое убывание критерия качества, совпадающее с направлением градиента. Затем данное направление проектируется на гиперплоскость, касательную к границе допустимой области в рассматриваемой точке. Так как ограничения нелинейны, то только малая вариация вдоль полученного направления уменьшает минимизируемую

150