
Динамика и прочность машин. Методы возмущений
.pdf
Уравнение (3.10) далее интегрируется [5] (примем для упрощения 0 ):
u(t) A sn(K (k) t, k) , |
(3.11) |
где sn – обозначение эллиптического синуса Якоби, K – значение полного
эллиптического интеграла первого рода, |
A, k, – параметры, выражающиеся |
||||||||||||||||
следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
1 1 4 E(1,0) |
, |
|
k 2 |
1 |
|
1 4 E(1,0) |
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
|
1 4 E(1,0) |
(3.12) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(1 1 4 E(1,0)). |
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Профиль функции (3.11) представляет собой периодические, но не гармонические, кноидальные волны. Через модуль k форма этих волн зависит от энергии системы. При изменении E(1;0) в пределах от 0 до 14 1 амплитуда A изменяется от 0 до 1/2 , аналог частоты - от 1 до 1/ 
 2 , а модуль k –
2 , а модуль k –
в пределах его области изменения от 0 до 1. При малых E(1;0) A ~ 
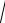 E(1;0) ,
E(1;0) ,
~ 1, k ~ 0 , sn ~ sin и K ~ / 2 , то есть мы имеем гармонические колебания линейного осциллятора. Нелинейность в (3.1) при этом фактически не проявляется. Отметим, в частности, что при малых мы получаем поправку фазы в аргументе (3.11) порядка t . Для того чтобы это увидеть, достаточно разложить функцию ( ) , определенную соотношениями (3.12), в степенной ряд и учесть, что t отдельно от в решение не входит. Исключая из первых двух соотношений (3.12) внутренний радикал, получаем: ~ 1 14 A2 , то есть
поправка частоты пропорциональна квадрату амплитуды. Числовой множитель в этой оценке не точен, поскольку нужно учитывать зависимость эллиптического синуса от модуля k и модуля от A2 (мы получим его точное значение в первом приближении ниже).
Попытаемся получить равномерно сходящееся асимптотическое разложение решения (3.1)–(3.2) и обнаруженную выше поправку к частоте с помощью метода многих масштабов. Уже ясно, что для этого достаточно в первом приближении считать функции в ряде (3.3) зависящими от двух аргументов t и t :
u(t, ) u0 (t, ) u1(t, ) ... |
(3.13) |
||||||
Производную в (3.1) заменяем частными производными: |
|
||||||
|
d 2 |
|
2 |
|
2 |
|
|
|
|
|
|
2 |
|
... |
(3.14) |
|
dt2 |
t2 |
t |
||||
Подставляя (3.13) и (3.14) в уравнение (3.1), получим:
21
(u , 2 u , |
u , ...) u u ... |
(u3 |
3 u2u ...) 0 . |
|||
0 tt |
0 t |
1 tt |
0 |
1 |
0 |
0 1 |
Выделяя в этом уравнении коэффициенты при степенях малого параметра и приравнивая их нулю, получаем:
0 : |
u , |
u |
0 ; |
|
|
|
(3.15) |
|
0 tt |
0 |
|
|
|
|
|
1 : |
u , |
u u3 2u , |
; |
(3.16) |
|||
|
1 tt |
1 |
0 |
|
0 t |
|
|
2 : |
… |
|
|
|
|
|
|
Общее решение уравнения (3.15) имеет вид |
|
||||||
|
|
|
u |
0 |
a( ) exp(it) a ( ) exp( it) . |
(3.17) |
|
|
|
|
|
|
|
|
|
Здесь, как и в предыдущей главе, мы использовали более компактное комплексное представление решения. С учетом (3.17) уравнение (3.16) примет вид
u1,tt u1 (a exp(it) a exp( it))3 2ia, exp(it) 2ia , exp( it) ,
после возведения в куб преобразующийся следующим образом:
u , |
u |
(2ia, |
|
3a2a )exp(it) (2ia , |
|
3a 2a)exp( it) |
1 tt |
1 |
|
|
|
||
|
|
a3 exp(3it) a 3 exp( 3it). |
|
(3.18) |
||
Источником вековых членов в частном решении (3.18) являются слагае-
мые с exp(it ) и exp( it) , которые можно удалить, если потребовать |
|
||
2ia, |
|
3a2a 0. |
(3.19) |
|
|
|
|
Для получения первого приближения равномерно сходящегося решения само уравнение (3.18) решать необязательно. Решение уравнения (3.19) ищем в виде
|
|
a |
1 |
Aexp(i ) , |
(3.20) |
||||
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
A2 . |
(3.21) |
||||
|
|
|
|||||||
|
|
8 |
|
|
|||||
Собирая (3.17), (3.20) и (3.21), получаем |
|
||||||||
u |
|
Acos((1 |
3 |
A2 )t ) O( ) . |
(3.22) |
||||
0 |
|
||||||||
|
8 |
|
|
|
|
||||
Для получения поправок к амплитуде и форме периодического решения необходимо учитывать в (3.3) члены более высокого порядка.
22
4.ДИНАМИЧЕСКАЯ СИСТЕМА
СПАРАМЕТРИЧЕСКИМ ВОЗБУЖДЕНИЕМ
Обратимся теперь к интереснейшему явлению параметрических колебаний. Попутно продемонстрируем на этом примере, как методы возмущений способны справиться с математическими трудностями, связанными с неавтономностью системы – зависимостью ее коэффициентов от независимой переменной.
Классическое исследование в этом направлении выполнил П.Л. Капица [7] (ссылки на исчерпывающий список работ имеются в статье [6]). Он экспериментально и теоретически изучил поведение маятника с вибрирующей осью подвеса и показал, что верхнее вертикальное положение равновесия может быть устойчивым. Вибрация может повысить устойчивость механических систем; ярким примером этого является индийская магическая веревка,
вертикальная вибрация которой делает |
|
|
||||||
мягкую веревку жесткой настолько, что |
|
|
||||||
ее верхнее вертикальное положение ста- |
|
|
||||||
новится устойчивым. |
|
|
|
|
|
|||
Выведем уравнение динамики пере- |
|
|
||||||
вернутого маятника с вибрирующей точ- |
|
|
||||||
кой подвеса. С этой целью выберем не- |
|
|
||||||
инерциальную |
систему |
отсчета |
|
|
|
|||
с началом O на конце маятника и векто- |
|
|
||||||
рами координатного репера вдоль оси ма- |
|
|
||||||
ятника и перпендикулярно ей (рис. 4.1). |
|
|
||||||
Закон изменения количества движения в |
|
|
||||||
этой системе отсчета получается преобра- |
|
|
||||||
зованием из инерциальной системы от- |
|
|
||||||
счета |
, в которой закреплено устрой- |
Рис. 4.1. Схема перевернутого |
||||||
ство, |
вибрирующее точку подвеса |
P . |
||||||
|
маятника |
|||||||
Пусть |
r0 {0, l} |
– радиус-вектор |
точки |
|
||||
|
|
|||||||
P отно |
|
|
|
|
|
|
||
сительно системсительно |
системы |
отсчета , |
r {0, a cos t} – радиус- |
|||||
|
|
|
|
|
|
|
0 |
|
вектор этой точки относительно , |
r |
и r – радиусы-векторы произвольной |
||||||
23

точки M относи и |
соответственно, а |
cos |
sin |
O |
– матрица по- |
||
|
|
sin |
cos |
ворота координатного репера системы |
к координатному реперу системы |
||
. Рассмотрим трансляционный вектор с началом в точке P и концом в точ- |
|||
ке M . С точки зрения |
этот вектор задается радиусом-вектором r r0 , |
||
а с точки зрения он же задается радиусом-вектором, выражаемым разно-
стью определенных в ней радиусов-векторов |
r r . Связь двух представле- |
|||||||||
|
|
|
|
|
|
|
|
|
0 |
|
ний рассматриваемого трансляционного вектора выражается формулой |
|
|||||||||
|
|
|
|
|
r r O (r r ) . |
(4.1) |
||||
|
|
|
|
|
0 |
|
|
0 |
|
|
Дифференцируя (4.1) по времени и исключая |
r r с помощью нее же, по- |
|||||||||
|
|
|
|
|
|
|
|
|
0 |
|
лучим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
v v |
0 |
O (v v ) Ω (r r ) |
(4.2) |
||||
|
|
|
|
|
0 |
|
|
0 |
|
|
где Ω – спин вращения относительно , |
|
|
|
|
||||||
|
|
|
|
|
Ω O OT . |
|
|
(4.3) |
||
Дифференцируя |
(4.2) |
по времени и |
исключая r r с помощью |
(4.1) |
||||||
|
|
|
|
|
|
|
|
|
0 |
|
и v v с помощью (4.2), получим: |
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
a a |
0 |
O (a a ) 2Ω (v v |
0 |
) (Ω Ω2 ) (r r ) . |
(4.4) |
|||||
|
|
|
|
0 |
|
|
0 |
|
||
Вектор сил, действующих на материальную точку, преобразуется из в в соответствии с выражением
F O F . |
(4.5) |
В инерциальной системе отсчета имеет место закон изменения количества движения:
|
|
|
F ma . |
|
|
(4.6) |
С помощью (4.4), (4.5) он преобразуется в системе отсчета к виду |
|
|||||
F m(a a |
0 |
O a |
2Ω (v v |
) (Ω Ω2 ) (r r )) . |
(4.7) |
|
|
0 |
0 |
|
0 |
|
|
В нашем случае точку M удобно расположить на конце маятника. Тогда |
||||||
r v a 0. По определению r0 , кроме того, |
v0 a0 0 . По формуле (4.3) |
|||||
вычисляем |
|
|
|
|
|
|
24

0 |
1 |
|
1 |
0 |
0 |
1 |
Ω |
, Ω2 |
2 |
|
, |
Ω |
. |
1 |
0 |
|
0 |
1 |
1 |
0 |
Понадобится a0 {0, a 2 cos t} , |
а также |
F {0, N} mg{sin , cos } , |
||||
где N – сила реакции. Подставляя все это в (4.7), получаем первое уравнение |
||||||
в виде |
|
|
|
|
|
|
|
l (g a 2 cos t)sin 0 |
|
||||
(второе определяет силу реакции |
N и нам не потребуется). Мы будем рас- |
|||||
сматривать малые отклонения от состояния равновесия, когда sin и наше уравнение принимает вид
l (g a 2 cos t) 0 .
Обезразмеривая время следующим образом: t 2t , получим новую форму уравнения
|
|
|
( 2 cos 2t) 0 |
(4.8) |
|
где |
4g |
, |
4 a , а черта над t опущена. Если представить (4.8) в форме |
||
2 |
|||||
|
|
l |
|
||
|
|
|
( 2 cos 2t) 0 |
(4.9) |
|
и считать здесь и абстрактными параметрами, принимающими положительные и отрицательные значения, то мы придем к более общему модельному уравнению для изучения параметрических колебаний, называемому уравнением Матье, с которым далее и будем иметь дело. Кроме того, будем считать | | 1, что позволяет применить метод возмущений.
Но сначала изучим общие свойства уравнения Матье, не решая его. Уравнение (4.9) имеет трансляционную симметрию по независимой переменной t с периодом n : если 1(t) – его решение, то и 1(t n ) тоже его решение, что легко проверить, заменяя t аргументом t n . Мы будем считать, что два линейно независимых решения уравнения второго порядка (4.9)
1(t) и 2 (t) удовлетворяют начальным условиям: |
|
||
1(0) 1, |
1(0) 0; |
(4.10) |
|
2 (0) 0, |
2 (0) 1 |
||
|
|||
25

(определитель Вронского гарантированно не равен нулю при t 0). Функции1(t ) и 2 (t ) являются решениями уравнения Матье, а значит, они раскладываются по базису решений этого уравнения 1(t) и 2 (t) :
1(t ) a11 1(t) a12 2 |
(t); |
(4.11) |
|
2 (t ) a21 1(t) a22 2 (t). |
|||
|
|||
Коэффициенты aij в формулах (4.11) определяются однозначно начальными условиями (4.10), отсюда
a11 1( ), |
a21 2 ( ); |
a12 1( ), |
a22 2 ( ). |
Соотношения (4.11) в матричной форме записываются так:
(t ) A (t) ,
|
|
|
, |
a |
a |
|
где |
1 |
|
A 11 |
12 |
. |
|
2 |
|
|
a21 |
a22 |
|
|
Положим
(t) P (t) ,
(4.12)
(4.13)
(4.14)
где матрица P не вырождена и от времени не зависит. Подставим (4.14) в (4.13), в результате чего получим:
(t ) B (t) , B P A P 1 . (4.15)
Матрица B имеет собственные числа, совпадающие с собственными
числами матрицы A : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 , |
1 |
(a |
a ) , |
(4.16) |
|
|
|
|||||||
1,2 |
|
2 |
11 |
22 |
|
|||
определяемыми из характеристического уравнения |
|
|||||||
|
|
2 2 1 0 . |
|
(4.17) |
||||
Если 1, то собственные числа различны, в противном случае они совпадают, оба принимая значение либо 1, либо –1. Мы потребуем, чтобы
26
матрица P приводила матрицу A к простейшей, жордановой канонической, форме. Тогда, если 1, матрица B имеет вид
|
|
|
|
0 |
|
|
|
(4.18) |
||
|
|
B |
1 |
|
|
|
. |
|
|
|
|
|
|
0 |
2 |
|
|
|
|||
В противном случае |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
(4.19) |
||
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
||
либо |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
(4.20) |
||
|
|
B |
|
|
|
|
. |
|
|
|
|
|
|
1 |
1 |
|
|
|
|||
Если матрица B имеет диагональную форму (4.18) или (4.19), то соот- |
||||||||||
ношение (4.15) можно переписать так: |
|
|
|
|
|
|
|
|||
1(t ) 1 1(t), |
|
2 (t ) 2 2 (t) , |
(4.21) |
|||||||
откуда следует: |
|
|
|
|
|
|
|
|
|
|
(t n ) n (t), |
|
|
2 |
(t n ) n |
2 |
(t) . |
(4.22) |
|||
1 |
1 |
1 |
|
|
|
2 |
|
|
||
При t |
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
| i | 1; |
|
|
|
|||
|
i (t) |
|
| i | 1, |
|
|
(4.23) |
||||
|
|
, |
|
|
|
|||||
то есть решение неограниченно растет во времени, если величина какоголибо из собственных чисел больше единицы, и затухает, если оба собственных числа по модулю меньше единицы. В случае кратных собственных значений (4.22) показывает, что решения периодичны: с периодом , если 1, и с периодом 2 , если 1. Таким образом, случаи кратных корней отделяют устойчивые значения от неустойчивых.
Соотношения (4.21) можно использовать для записи решений в нормальной форме Флоке. Для этого умножим первое из них на exp( 1(t )) и получим:
exp( 1(t )) 1(t ) 1 exp( 1 )exp( 1t) 1(t) .
Если потребовать, чтобы 1 exp( 1 ) 1, что равносильно требованию
|
1 ln , то наше равенство примет вид |
|
|
1 |
|
1 |
|
|
|
||
|
|
exp( 1(t )) 1(t ) exp( 1t) 1(t) , |
(4.24) |
27
означающий периодичность функции exp( 1t) 1(t) 1(t) с периодом . Таким образом, оба решения можно представить в нормальной форме:
i (t) exp( it) i (t) , |
(4.25) |
где i – в общем комплексные числа, называемые характеристическими по-
казателями,
|
|
|
|
|
1 ln . |
|
|
(4.26) |
||
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
||
Если матрица B имеет форму (4.20), то в этом случае можно аналогич- |
||||||||||
ным образом привести решения к форме |
|
|
|
|
||||||
1(t) exp( t) 1(t), |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
t |
(4.27) |
(t) exp( t)( (t) |
|
(t)), |
||||||||
|
|
|||||||||
|
2 |
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
где 1 ln . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из (4.16) следует, что при | | 1 |
одно из собственных значений, 1 , бу- |
|||||||||
дет больше единицы, в то время как второе, |
2 , в силу соотношения 1 2 1, |
|||||||||
следующего из теоремы Виета для уравнения (4.17), будет меньше единицы. Из (4.26) тогда следует, что вещественная часть одного из характеристических показателей i положительна, а второго – отрицательна. Из (4.23) или (4.25) и (4.27) следует, что одно из решений будет неограниченно расти со временем, а второе оставаться ограниченным. На рис. 4.2 показаны возможные типы неограниченных решений.
28
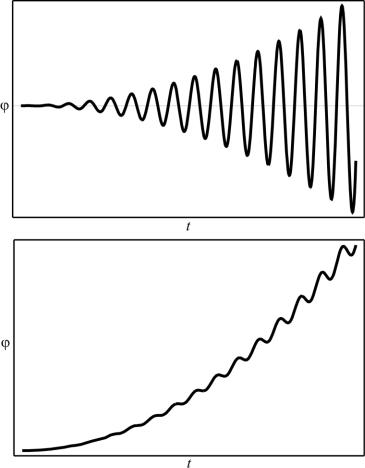
Рис. 4.2. Неограниченные решения уравнения Матье
При | | 1 собственные числа i представляют собой сопряженные комплексные числа, модули которых равны единице, так что вещественные части характеристических показателей i равняются нулю. Этому случаю соответствуют ограниченные и, в общем, апериодические решения, меняющиеся с двумя частотами – мнимой частью i и частотой возбуждения, равной 2. В зависимости от соотношения этих частот решение может принимать разнообразные формы (рис. 4.3).
29
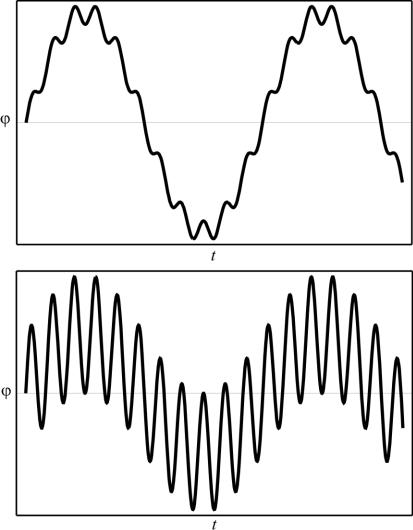
Рис. 4.3. Ограниченные решения уравнения Матье
Переход от устойчивых движений к неустойчивым происходит при | | 1, что соответствует кратным корням 1 или 1 и характеристическим показателям 0 или i . Оба режима – периодические, первый с периодом , второй с периодом 2 . Переходные кривые, разделяющие плоскость параметров , на области устойчивости и неустойчивости, показаны на рис. 4.4.
30
