
Вероятностные методы расчета конструкций
..pdf
qкр |
2 Eh2 |
|
|
, |
|
12(1 2 )r2 |
||
где определяется согласно условиям закрепления (для шарнирного опирания 0,425 ).
Отсюда
h |
q кр12(1 2 )r2 |
|
|
26 104 |
12 (1 0,09) |
1,84 10 |
2 |
м. |
||||||||||||||
|
|
|
|
2 |
E |
|
|
|
|
0,425 |
3,14 |
2 |
|
11 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 10 |
|
|
|
|
|||||||
Номинальная толщина |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
h |
|
|
|
h |
|
|
|
|
1,84 10 2 |
|
|
1,84 10 2 |
|
2,05 10 |
2 |
м. |
||||||
1 |
|
|
A |
1 |
3 0,0346 |
|
0,897 |
|
||||||||||||||
ном |
|
h |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Искомая толщина h (2,05 0,21) 10 2 |
м. |
|
|
|
|
|||||||||||||||||
Таким образом, нормальный закон распределения всех случайных величин позволяет получить простое замкнутое решение при определении параметров системы по заданной надежности.
Но законы распределения нагрузки и несущей способности могут быть самыми различными. Поэтому не всегда удается получить простые формулы для определения K, подобные полученным для случая нормального распределения. Однако для некоторых комбинаций законов распределения нагрузки и несущей способности это удается [12].
При оценке работоспособности по прочности, например, примем, что нагрузка и несущая способность подчиняются экспоненциальному закону, тогда имеем:
f3(q) = 3 exp[– 3(q – q0)]; |
f1(S) = 1 exp[– 1(S – S0)]. |
Числовые характеристики распределения имеют вид:
mS = S0 + 1/ 1; S = 1/ 1; |
mq = q0 + 1/ 3; |
q = 1/ 3. |
131
Поскольку R Kq , то
f2 |
(R) |
1 |
f3 |
|
R |
|
1 |
3e |
|
(R/ K q ) |
2e |
|
(R R ) |
, |
||
|
|
|
|
|
3 |
0 |
2 |
0 |
||||||||
K |
K |
|||||||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
K |
|
|
|
|
|
|
|
|
||||
где 2 3 |
/ K; R0 Kq0 . |
|
|
|
|
|
|
|
|
|
||||||
Тогда для определения надежности можно использовать уравнение (4.7):
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
H |
f1 (S)[ f2 (R)dR]dS. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
S |
f2 (R)dR S |
f2 (R)dR |
|
|||||||
|
|
|
|
|
|
|
|
|
R0 |
|
|
|
|
S |
2 exp[ 2 (R R0 )]dR 1 exp[ 2 (S R0 )], |
||||||||||||
R0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
0 |
|
|
2 |
|
0 |
|
H |
|
|
|
|
exp[ |
(S |
|||||||
|
|
exp[ (S S |
)] 1 |
|
R )] dS, |
||||||||
|
S0 |
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
H 1 |
|
|
|
exp[ 2 (S0 R0 )]. |
||||||
|
|
|
|
1 |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Поскольку 2 = 3/K и R0 = Kq0, то, подставляя их в полученное выражение, имеем для надежности следующее уравнение:
H 1 |
K |
|
|
|
|
S |
|
|
|
|
|
1 |
exp |
3q0 |
|
3 |
|
0 |
|
, |
|
K 1 |
3 |
|
||||||||
|
|
|
|
K |
|
|
|
|||
которое любым приближенным способом можно разрешить относительно K.
Иногдаприрешенииэтоуравнениеудобнеепредставитьввиде
|
|
3 |
|
|
|
|
|
S |
|
|
|
(1 H ) 1 |
|
|
exp |
3q0 |
|
3 |
|
0 |
. |
(4.12) |
|
K 2 |
|
||||||||||
|
|
|
|
|
|
K |
|
|
|
||
132

Для частного случая, когда q0 S 0 0 , решение можно получить в замкнутом виде:
|
H 1 |
K 1 |
|
, |
|
K |
3 |
||
|
|
1 |
|
|
откуда K |
3 (1 H ) . |
|
|
|
|
1H |
|
|
|
Пример 4.8 [3]. Сферический купол (рис. 4.3) радиусом r = 1 м нагружен случайным давлением q c экспоненциальным
законом распределения, у которого 3 5,75 1/МПа, q0 2 МПа.
Кромки купола шарнирно оперты на упругое опорное кольцо. Материал оболочки и кольца одинаков, его несущая способность имеет экспоненциальный закон распределения с па-
раметрами 1 0,011 1/МПа, Рис. 4.3
S0 = 300 МПа.
Найти толщину оболочки h и площадь поперечного сечения F опорного кольца, чтобы надежность конструкции была 0,99.
Решение. Если подставить заданные значения в уравнение (4.12), то для заданного Н = 0,99 получим значение корня
K = 113,576. |
|
|
|
|
|
|
|
r |
|
|
|
|
|
||
Для сферического купола K |
|
, следовательно, |
|
||||||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2h |
|
|
|
|
|
h |
|
r |
|
|
|
|
1 |
|
4,4 10 3 |
|
м. |
|
|||
2K |
|
2 113,576 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
Для кольца имеем: |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
rh |
|
|
|
|
|
r |
2 |
sin |
cos 0,39 |
|
|
|
|
||||||
|
|
r sin |
|
||||||||||||
K |
|
|
|
|
|
|
. |
(4.13) |
|||||||
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
F 0,39h rh |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
133

Примем 60 . Тогда, решая уравнение (4.13) относительно F, получим: F = 1,678·10–3 м2.
Если работоспособность конструкции оценивается по же-
|
wзад |
|
|
|
|
|
||
сткости, то надежность Н |
f (w)dw . Если w K*q и извес- |
|||||||
|
|
0 |
|
|
|
|
|
|
тен закон f3 (q) , то f (w) |
1 |
|
|
w |
. Например, если нагруз- |
|||
|
|
|
f3 |
|
|
|
||
K |
* |
|
K |
* |
||||
|
|
|
|
|
|
|
||
ка имеет равномерное распределение, т.е.:
|
|
|
|
, если a q b; |
|
|
|
|||||||
|
|
f3 (q) |
если |
a q |
|
или q b, |
|
|||||||
|
|
|
|
0, |
|
|
||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
если a |
|
w |
|
b; |
|
|
|
||
|
|
|
K* |
|
|
|
|
|||||||
|
f (w) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
w |
|
|
w |
|
||||
|
K* |
|
|
|
|
|
|
|||||||
|
|
|
|
|
a |
|
|
b, |
||||||
|
|
|
|
0, |
если |
|
|
|
или |
|
|
|||
|
|
|
|
K |
* |
|
K |
* |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
b a |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wзад
Следовательно, Н
aK*
Отсюда
K*
f (w)dw wзад аK* .
K* (b a)
wзад |
|
H (b a) a . |
(4.14) |
Пример 4.9 [3]. Равносторонняя треугольная пластина, шарнирно опертая по всему контуру (рис. 4.4), нагружена случайной силой q, приложенной в центре масс (ЦМ). Нагрузка распределена с равной вероятностью в пределах (1…2)·104 Па. Необходимо подобрать толщину пластины так, чтобы ее надежность по жесткости была равна 0,99 при wзад = 0,32·10–2 м.
134
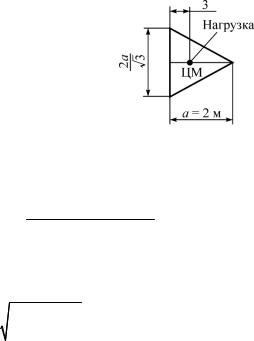
Решение. |
По |
заданным Н |
|||||
и wзад определяем K* по форму- |
|||||||
ле (4.14): |
|
|
|
|
|
|
|
|
K* |
|
|
wзад |
|
|
|
|
H (b a) a |
|
|||||
|
|
|
|
|
|||
|
|
0,32 10 2 |
|
|
|||
0,99 (2 1) 104 |
1 104 |
||||||
16 10 8 |
м/Н. |
Рис. 4.4 |
|
Для шарнирно опертой пластины
K* 0,00575a2 12(1 2 ) .
Eh3
Подставляя в эту формулу полученное значение и следующие величины: 0,3; Е 2 1011 Па; а = 2 м, получим:
h 3 125,8 108 14 1,987 10 2 м. 16 10
В случае определения параметров конструкции по устойчивости при заданной надежности имеем:
qкр
Н f (q)dq.
0
Если нагрузка имеет распределение Вейбулла, т.е.
|
|
|
|
|
|
|
(q ) |
|
|
|||
f3 (q) |
|
(q ) 1 exp |
, |
|||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(q ) |
|
(qкр ) |
|
|
|
|||||
H 1 exp |
|
|
|
|
или |
|
|
|
ln(1 H ). |
|||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||
135
Решая это уравнение относительно qкр , получим:
qкр |
|
ln(1 H ) . |
(4.15) |
|
|
|
Пример 4.10. На прямоугольную пластину длиной 2 м, шириной 1 м действует сжимающая распределенная нагрузка q, величина которой случайна и распределена по закону Вейбулла с параметрами: γ = 0; β = 3; α = (2247·103)2 Н3/м3. Края пластины шарнирно оперты. Найти толщину пластины h, обеспечивающую надежность по устойчивости H = 0,99.
Решение. По заданным Н и α определяем qкр по форму-
ле (4.15):
qкр ln(1 H ) 3 (2247 103 )3 ln(1 0,99) 3,718 106 Н/м.
Для рассматриваемой пластины |
q |
|
c 2 Eh3 |
. |
|
b212(1 2 ) |
|||||
|
кр |
|
|||
Для заданного соотношения сторон a / b 2 и шарнирного закрепления сторон с = 4, а потому
h 3 qкрb212(1 2 ) 1,72 10 2 м.
4.3. Надежность систем при динамическом нагружении
При оценке надежности конструкций, подверженных случайным по времени нагрузкам, обычно выделяют три типа задач [2]. Во-первых, это задачи расчета конструкций под действием нестационарных случайных нагрузок с высоким уровнем напряжений. К таким нагрузкам можно отнести сейсмические и ударные нагрузки. Главным вопросом при решении подобного рода задач является определение вероятности хотя бы однократного достижения обобщенным параметром х(t) внешней нагрузки предельного значения Rпр за время эксплуатации конструкции (рис. 4.5, а).
136
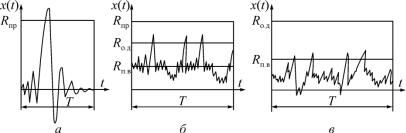
Рис. 4.5
Во-вторых, это задача о накоплении остаточных деформаций в конструкциях, которые находятся под действием стационарных случайных нагрузок (рис. 4.5, б). При этом предполагается, что нагрузки не достигают предельных значений, однако возможно появление остаточных деформаций Rо.д. Основным вопросом в этом случае является вопрос отыскания функции распределения вероятности остаточных деформаций, например, к концу срока службы конструкции. Подобные задачи встречаются, например, при расчете строительных конструкций на ветровую или снеговую нагрузку, при расчете конструкций на транспортную нагрузку и т.д.
В-третьих, это задачи об усталостных разрушениях конструкций под действием стационарных случайных сил (рис. 4.5, в). Предполагается, что материал конструкции не выходит за предел выносливости Rп.в, а причиной разрушения являются усталостные трещины. Эти задачи актуальны для авиационных и машиностроительных конструкций.
Таким образом, основной задачей является определение вероятности того, что случайная функция в течение заданного интервала изменения своего аргумента не превысит допустимого уровня (так называемая задачао выбросах случайной функции [15], [25]).
Общие формулы для определения вероятности выброса в единицу времени и среднего времени пребывания функции выше заданного уровня можно получить для любого непрерывного случайного процесса [22]. Однако численный результат
137

можно получить просто только для нормальных случайных процессов, определение же закона распределения времени пребывания функции выше заданного уровня является значительно более сложной задачей и даже для нормальных процессов требует сложных расчетов.
4.3.1. Выбросы и решение задач надежности
Итак, пусть X (t) – непрерывный случайный процесс, а –
значение ординаты этой функции, превышение которого (выбросы за которое) нас интересует. Определим вероятность того, что за бесконечно малый промежуток времени dt, непосредственно следующий за моментом времени t, произойдет выброс [22]. Для того чтобы выброс действительно имел место, необходимо реализовать два события: во-первых, в момент времени t ордината случайной функции должна быть меньше а, во-вторых, в момент времени (t + dt) ордината должна быть больше а, т.е.:
X (t) a, |
X (t dt) a. |
(4.16) |
Полагая скорость изменения случайной функции v(t) dx / dt
постоянной в течение времени dt, можно с точностью до бесконечно малых второго порядканаписать:
X (t dt) X (t) v(t)dt.
Тогда X (t) a v(t)dt, и вместо двух неравенств (4.16) получим одно:
a v(t)dt X (t) a при v(t) 0.
Введем в рассмотрение двумерный закон распределения ординаты случайной функции и ее скорости f (x,v t) в один
и тот же момент времени t, тогда вероятность выброса в интервале времени dt может быть записана в следующем виде:
|
a |
||
P a v(t)dt X (t) a |
f (x,v |
|
t)dxdv. |
|
|||
|
|||
0 a vdt
138

Пределы интегрирования охватывают все значения X(t) и v(t), удовлетворяющие неравенствам (4.16). Внутренний интеграл может быть вычислен сразу по теореме о среднем, так как у него пределы отличаются на бесконечно малую величину:
a |
f (x,v |
|
t)dx v dt f (a,v |
|
t), |
|
|
||||
|
|
|
|
|
a vdt
поэтому
P a v(t)dt X (t) a dt f (a,v t)vdv.
0
Если разделить вероятность выброса на время dt, в течение которого он ожидается, то получим временную плотность вероятности выброса за уровень а в момент t (среднее число выбросов в единицу времени):
|
|
|
|
||||
p(a |
|
t) f (a,v |
|
t)vdv. |
(4.17) |
||
|
|
||||||
|
|
|
|||||
0 |
|
|
|
|
|
||
Тогда |
|
||||||
P a v(t)dt X (t) a p(a |
|
t)dt. |
(4.18) |
||||
|
|||||||
Данный интеграл представляет собой математическое ожидание положительной скорости v(t). Пользуясь полученным выражением, можно найти среднее время пребывания случайной величины X(t) выше заданного уровня a для любого промежутка времени T. Для этого разобьем промежуток Т на n равных по величине малых интервалов dtj, каждый из которых расположен вблизи момента времени tj (j = 1, …, n). Вероятность того, что ордината случайной функции X(tj) будет выше заданного уровня,
P X (t) a f (x t j )dx.
a
Будем считать интервалы dtj настолько малыми, что возможной сменой знака X(t) внутри интервала можно пренебречь. Тогда, если ввести в рассмотрение систему случайных величин
139
t j , равных по величине соответствующему интервалу, если
произошло превышение заданного уровня, и равных нулю, если такого превышения нет, то общее время Ta пребывания выше
n
заданного уровня а будет равно сумме t j , т.е. Ta t j .
j 1
Найдем математическое ожидание от обеих частей равенства (среднее время пребывания случайной функции выше заданного уровня):
n
mTa M[ t j ].
j 1
Поскольку величина t j может принимать только два значения ( t j или 0), то ее математическое ожидание равно произведению dtj на вероятность превышения функцией предела а:
|
|
|
||
|
|
dt j f (x |
|
t j )dx. |
|
||||
M t j |
|
|||
a
Переходя к пределу при n , получим среднее время пребывания случайной величины X(t) выше заданного уровня a для любого промежутка времени T:
T |
|
||
mTa f (x |
|
t)dxdt. |
(4.19) |
|
|||
|
|
||
0 a |
|
||
Определим среднее время пребывания случайной функции выше заданного предела в течение одного выброса mNa . Для этого
необходимо разделить среднее время пребывания mTa на среднее
число выбросов Na за время T. Для этого разобьем промежуток Т опять на n равных по величине малых интервалов dtj, каждый из которых расположен вблизи момента времени tj (j = 1, …, n), и введем вспомогательные величины Nj = 1 (если внутри интервала про-
140
