
m32444_3
.doc
ТЕМА 4. ВВЕДЕНИЕ В АНАЛИЗ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ
В ЗАДАЧАХ 31 - 40 найти указанные пределы.
31. 1)
![]()
2)
![]()
32. 1)
![]()
2)
![]()
1)
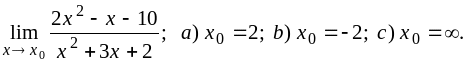
2)
![]()
1)
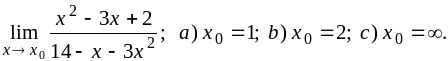
2)
![]()
1)
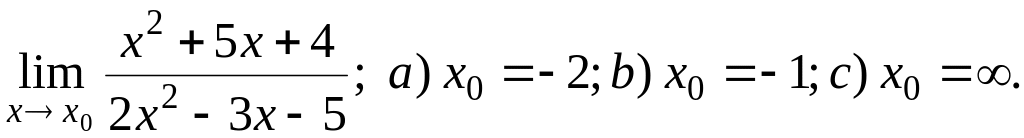
2)
![]()
1)

2)
![]()
1)
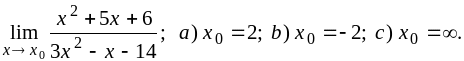
2)
![]()
1)
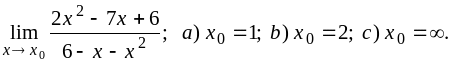
2)
![]()
1)
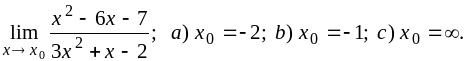
2)
![]()
1)

2)
![]()
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ.
1)
![]()
2)
![]()
При подстановке
вместо переменной
![]() ее предельного значения
ее предельного значения
![]() получается неопределенность вида
получается неопределенность вида
![]() .
Для избавления от этого типа неопределенности
в нашем случае представим квадратные
трехчлены числителя и знаменателя в
виде произведений линейных сомножителей,
воспользовавшись известной формулой
.
Для избавления от этого типа неопределенности
в нашем случае представим квадратные
трехчлены числителя и знаменателя в
виде произведений линейных сомножителей,
воспользовавшись известной формулой
![]() ,
,
где
![]() –
корни квадратного трехчлена
–
корни квадратного трехчлена
![]() .
.
У нас
![]()
так как дискриминант
квадратного трехчлена
![]() ,
а следовательно,
,
а следовательно,
![]()
Аналогично
![]() .
.
Теперь условие примера можно переписать в другом виде и продолжить его решение:
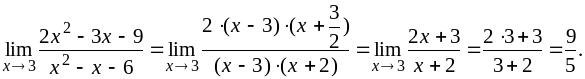
3)
![]()
Здесь сталкиваемся
с неопределенностью
![]() ,
избавиться от которой можно вынесением
за скобки в числителе и знаменателе
дроби переменной в старшей степени:
,
избавиться от которой можно вынесением
за скобки в числителе и знаменателе
дроби переменной в старшей степени:
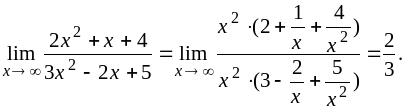
4)
![]()
В данном случае для освобождения от неопределенности будем использовать первый замечательный предел и одно из его очевидных следствий:
![]()
Решение примера будет выглядеть следующим образом:
![]()
![]()
ТЕМА 5. ПРОИЗВОДНАЯ ФУНКЦИИ ОДНОЙ
ПЕРЕМЕННОЙ
В ЗАДАЧАХ 41 - 50
найти
производные
![]() заданных функций, пользуясь правилами
и формулами дифференцирования.
заданных функций, пользуясь правилами
и формулами дифференцирования.
41. a)
![]() b)
b)
![]()
c)
![]() d)
d)
![]()
a)
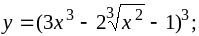 b)
b)
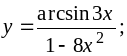
c)
![]() d)
d)
![]()
a)
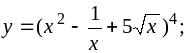 b)
b)
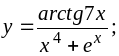
c)
![]() d)
d)
![]()
a)
 b)
b)
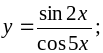
c)
![]() d)
d)
![]()
a)
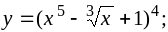 b)
b)
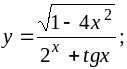
c)
![]() d)
d)
![]()
a)
 b)
b)
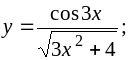
c)
![]() d)
d)
![]()
a)
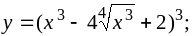 b)
b)
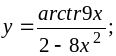
c)
![]() d)
d)
![]()
a)
 b)
b)

c)
![]() d)
d)
![]()
a)
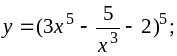 b)
b)

c)
![]() d)
d)
![]()
a)
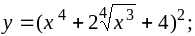 b)
b)
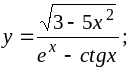
c)
![]() d)
d)
![]()
РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ. При решении всех последующих примеров, где требуется найти производные заданных функций, кроме таблицы производных основных элементарных функций (см. приложение 1) будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции:
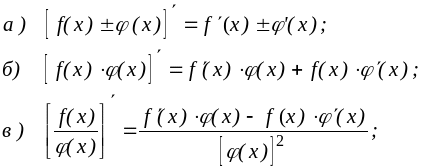
![]() если задана сложная
функция
если задана сложная
функция
![]() ,
где
,
где
![]() ,
то есть
,
то есть
![]() ;
если каждая из функций
;
если каждая из функций
![]() и
дифференцируема по своему аргументу,
то
и
дифференцируема по своему аргументу,
то
![]()
Решение.
![]()
![]()
![]()
2)
![]()
Решение.
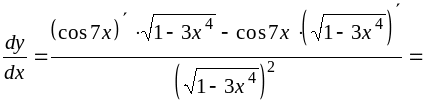
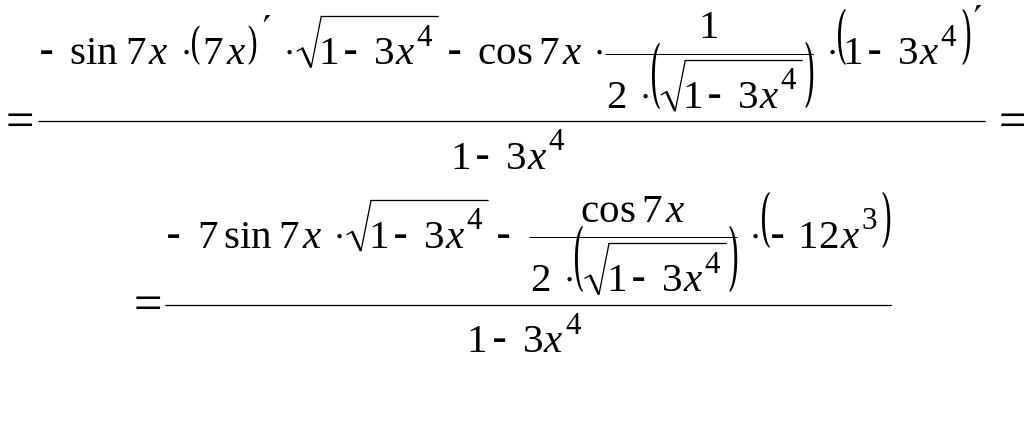
3)
![]()
Решение.
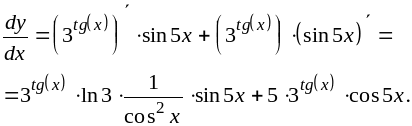
4)
![]()
Решение.
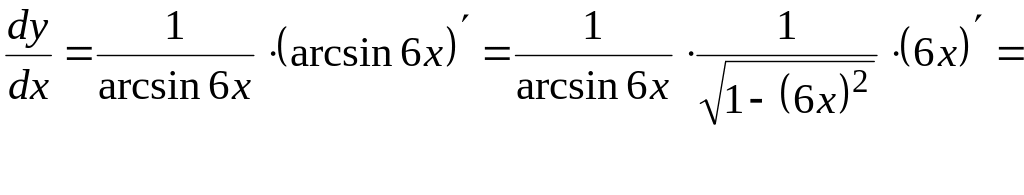

В ЗАДАЧАХ 51 - 60
задан закон
![]() изменения пути движения материальной
точки в зависимости от времени. Требуется
найти значения скорости и ускорения
этой точки в момент времени
изменения пути движения материальной
точки в зависимости от времени. Требуется
найти значения скорости и ускорения
этой точки в момент времени
![]() .
.
РЕШЕНИЕ ТИПОВОГО ПРИМЕРА. Пусть
![]()
Известно, что значения скорости и ускорения точки в некоторый момент времени являются значениями в этот момент соответственно первой и второй производных функции, задающей закон изменения пути движения точки.
У нас
![]() (ед. cк.);
(ед. cк.);
![]() (ед.
уск.).
(ед.
уск.).
