Тема 7.

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Основные понятия

Нормально распределенные случайные величины наиболее распространены на практике. Объяснение этому факту дал русский математик А.М. Ляпунов, доказав центральную предельную теорему.

Теорема. Если случайная величина Х равна сумме очень большого числа попарно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Приведем несколько примеров случайных величин, подчиняющихся нормальному закону распределения:

1. масса животного в определенном возрасте;

2. длина початка кукурузы;

3. жирность молока;

4. масса клубня картофеля.

Определение. Говорят, что непрерывная случайная величина Х имеет нормальное распределение (распределение Гаусса) с параметрами и ( , если плотность вероятностей этой случайной величины имеет вид

Влияние параметров a и  на вид кривой распределения, которую называют нормальной кривой, иллюстрируют рис. 7.1 – 7.3.

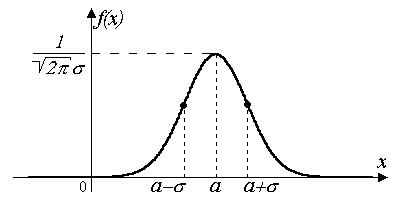
Рис. 7.1.

Рис. 7.2.

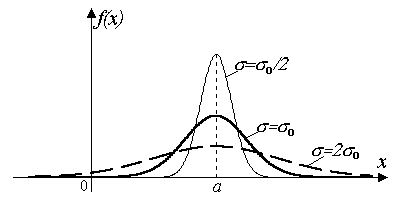
Рис. 7.3.

Можно показать, что если , то

Случайную величину X ~ N(0; 1) называют нормированной нормально распределенной или стандартной. Для нее законом распределения будет изученная ранее функция Гаусса (x) (см. схему Бернулли)

.

Отметим следующие важные факты: если , то справедливы формулы

(7.1)

и

(7.2)

Если в последней формуле заменить , то получим

.

Этот факт известен как правило трех сигм. Он означает, что практически все значения нормальной случайной величины находятся в интервале (рис. 7.4), который называют диапазоном изменения значений нормальной случайной величины.

Рис. 7.4.

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ К ТЕМЕ 7

Задача 7.1. Пусть , .

1. Найти параметры распределения а и .

2. Определить диапазон изменения значений случайной величины Х.

3. Вычислить а) 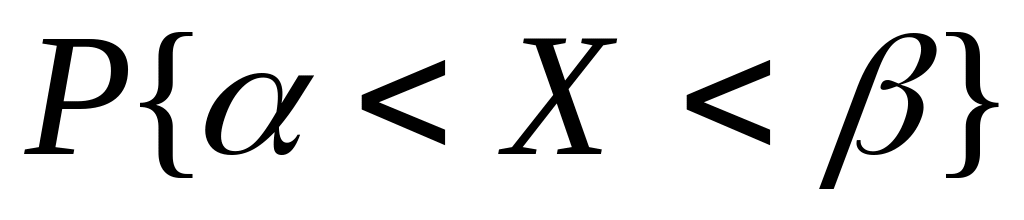, б) .

Вариант	1	2	3	4	5	6	7	8	9	10
	1,8	1,9	2,0	2,1	2,2	2,3	2,4	2,5	2,6	2,7
	13,1	13,2	13,3	13,4	13,5	13,6	13,7	13,8	13,9	14,0
	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09	0,10	0,11
	0,18	0,19	0,20	0,21	0,22	0,23	0,24	0,25	0,26	0,27

Вариант	11	12	13	14	15	16	17	18	19	20
	2,8	2,9	3,0	3,1	3,2	3,3	3,4	3,5	3,6	3,7
	14,1	14,2	14,3	14,4	14,5	14,6	14,7	14,8	14,9	15,0
	0,12	0,13	0,14	0,15	0,16	0,17	0,18	0,19	0,20	0,21
	0,28	0,29	0,30	0,31	0,32	0,33	0,34	0,35	0,36	0,37

Вариант	21	22	23	24	25	26	27	28	29	30
	3,8	3,9	4,0	4,1	4,2	4,3	4,4	4,5	4,6	4,7
	15,1	15,2	15,3	15,4	15,5	15,6	15,7	15,8	15,9	16,0
	0,22	0,23	0,24	0,25	0,26	0,27	0,28	0,29	0,30	0,31
	0,38	0,39	0,40	0,41	0,42	0,43	0,44	0,45	0,46	0,47

Пример решения индивидуального задания

Пример 7.1. Пусть известно, что , а также вероятности

1. Найти параметры распределения а и .

2. Определить диапазон изменения значений случайной величины Х.

3. Вычислить a) 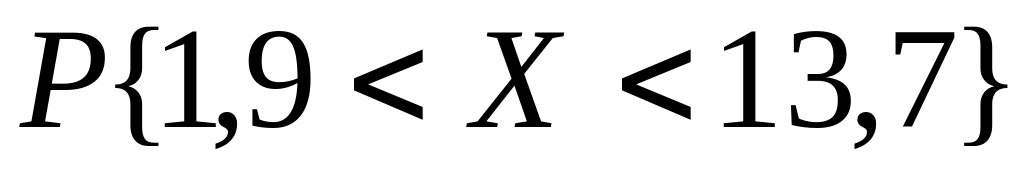, б) .

Решение.

1. Сначала отметим, что

и .

Теперь воспользуемся формулой (7.1)

:

По таблицам значений функции Лапласа (приложение 2) находим значение аргумента функции : , т.е.

(*)

Аналогично,

.

Отсюда

. (**)

Находим параметры распределения а и , решая систему уравнений (*) и (**):

.

Итак, теперь .

2. Согласно правилу трех сигм, диапазон изменения значений случайной величины имеет вид интервала

.

В нашем примере это интервал (12,9435,87; 12,94 + 35,87), т.е.

(4,67; 30,55).

3. Первую вероятность ищем по формуле (7.1)

,

а вторую по формуле (7.2)

:

а)

;

б)

КОНТРОЛЬНЫЕ ВОПРОСЫ К ТЕМЕ 7

1. Запишите вид функции плотности вероятностей нормального распределения. Какими параметрами определяется нормальное распределение? Каков их вероятностный смысл?

2. Начертите нормальную кривую. Каков геометрический смысл параметров нормального распределения? Как влияют на форму нормальной кривой параметры нормального распределения?

3. Как вычислить вероятность попадания в заданный интервал значений нормальной случайной величины? Каков геометрический смысл этой вероятности?

4. В чем суть правила «трех сигм»? Как найти диапазон изменения значений нормально распределенной случайной величины?

5. Случайная величина Х распределена нормально с математическим ожиданием, равным 25. Вероятность попадания ее значений в интервал (10; 15) равна 0,2. Чему равна вероятность попадания Х в интервал (35; 40)?

6. Пусть 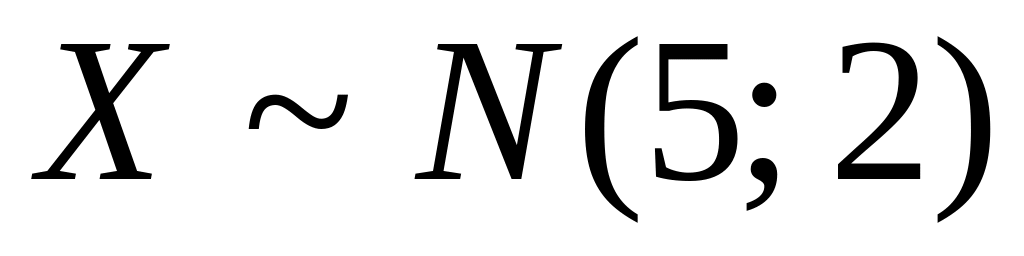. Каков диапазон изменения значений Х ?

7. Процентная жирность молока коров в хозяйствах некоторой области является нормальной случайной величиной с математическим ожиданием 3,1% и средним квадратическим отклонением 0,0225%. Вычислить вероятность того, что во взятой наугад пробе жирность молока будет колебаться в пределах от 2,8% до 3,5%. Каков диапазон колебания жирности молока?

8. Вес отдельного батона хлеба данной партии  случайная величина, описываемая нормальным законом распределения с математическим ожиданием 500 г и средним квадратическим отклонением 8 г. Определить вероятность того, что вес наудачу взятого из данной партии батона хлеба лежит в пределах от 496 до 508 г.

9. Средний размер диаметра стволов деревьев на некоторой делянке равен 25 см, а среднее квадратическое отклонение диаметров составляет 5 см. Считая, что диаметр ствола  случайная величина, распределенная нормально, найти: а) процент стволов, имеющих диаметр свыше 20 см; б) размер, который не превзойдет диаметр ствола дерева с вероятностью 0,96.

10. Вес карпа в некотором пруду является нормальной случайной величиной с математическим ожиданием 375 г и средним квадратическим отклонением 25 г. Какова вероятность того, что вес пойманного карпа будет а) в пределах от 325 г до 425 г; б) не более 400 г; в) не менее 350 г?

82