
m32352_9
.DOC
 .
.
b)
Применим подстановку
![]() .
Тогда
.
Тогда
 ,
,
откуда
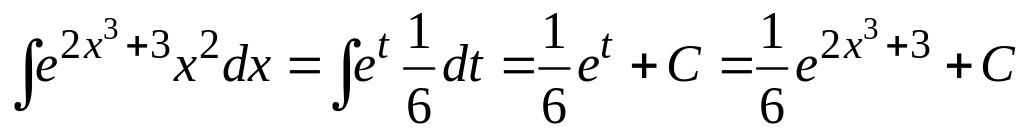 .
.
c) Применим формулу интегрирования по частям:
![]() .
.
Положим
![]() .
Тогда
.
Тогда
![]()
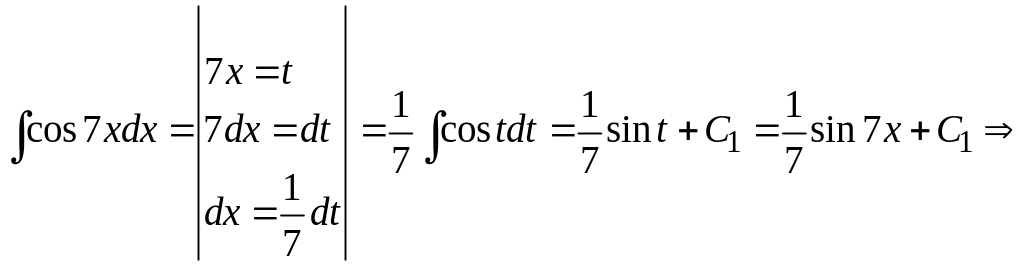
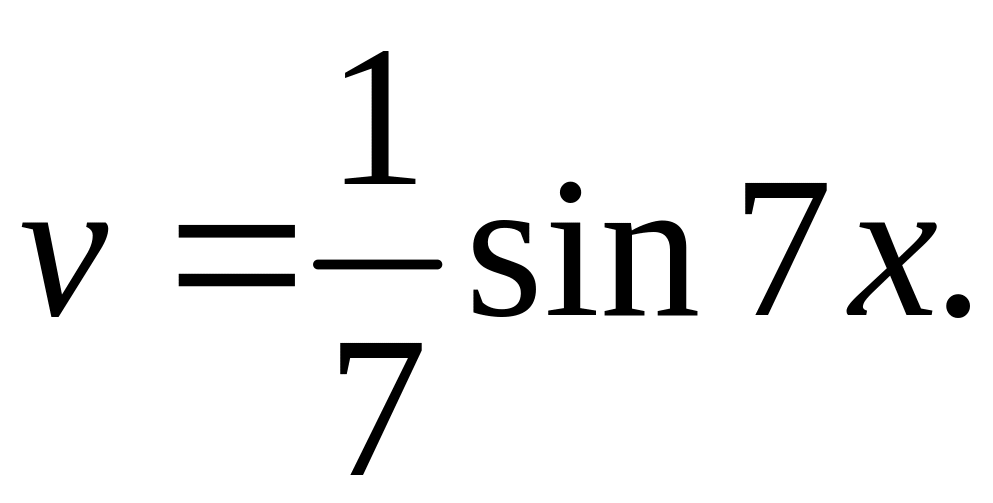
Таким образом,
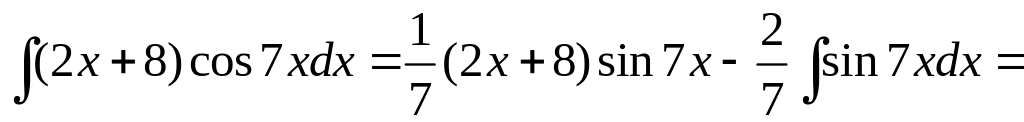
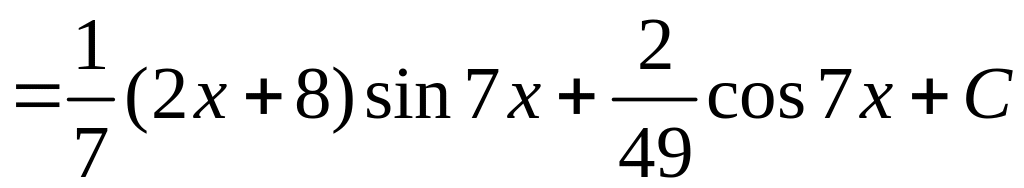 .
.
d) Здесь тоже воспользуемся формулой интегрирования по частям.
Положим
![]() .
.
Тогда
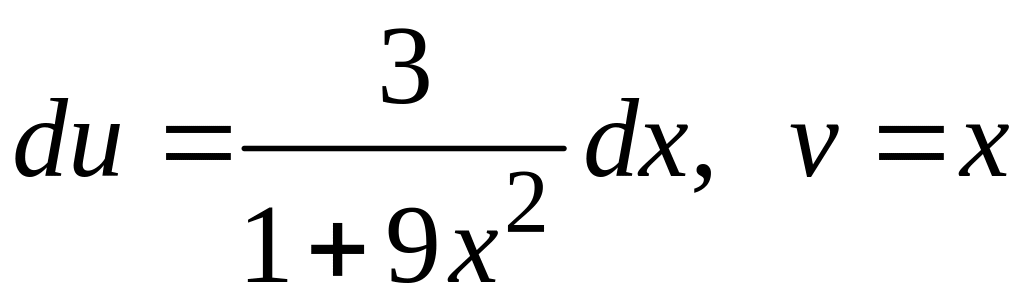 .
.
Отсюда
 .
.
Применяя
в последнем интеграле подстановку
![]() ,
получаем
,
получаем
![]() ,
следовательно,
,
следовательно,
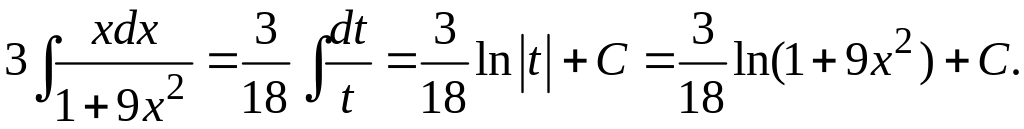
Теперь окончательно имеем
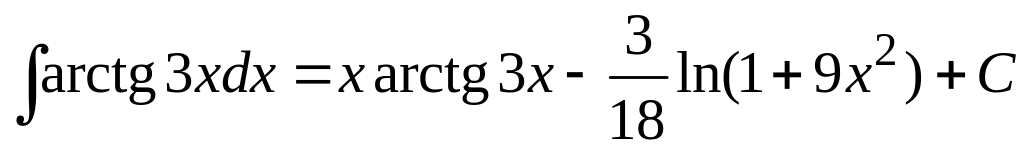 .
.
ПРИМЕР 2. Вычислить определенные интегралы:
a)
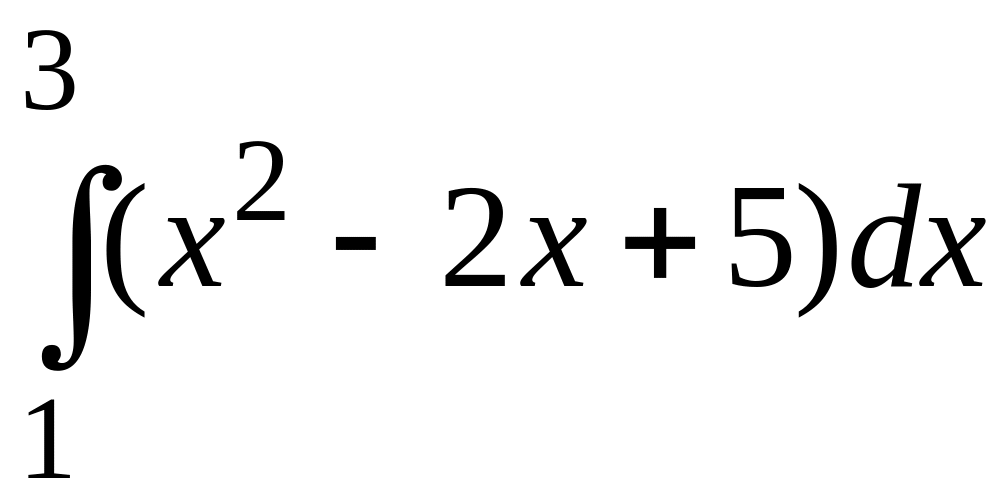 ;
b)
;
b)
 .
.
Решение.
a)
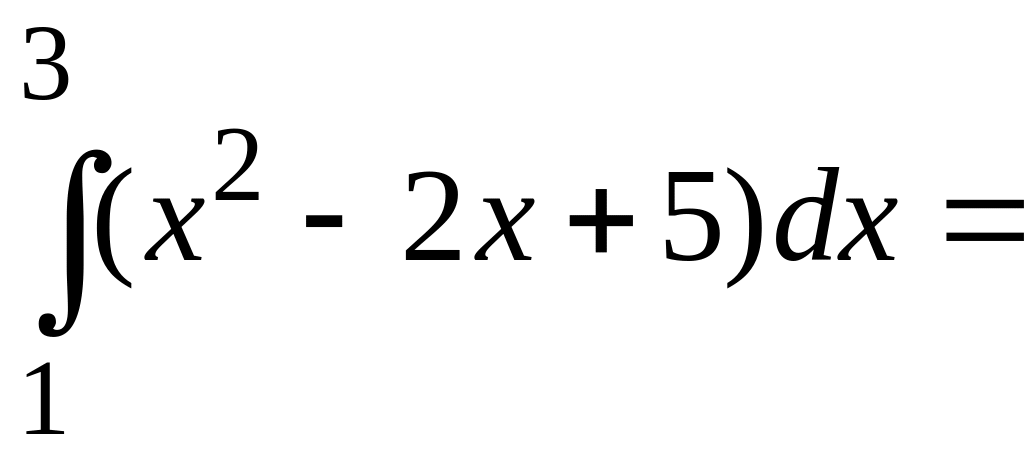
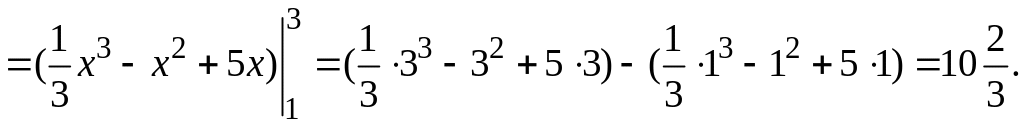
b)
Делаем замену
![]() .
Тогда, во-первых, при изменении старой
переменной интегрирования от
.
Тогда, во-первых, при изменении старой
переменной интегрирования от
![]() до
до
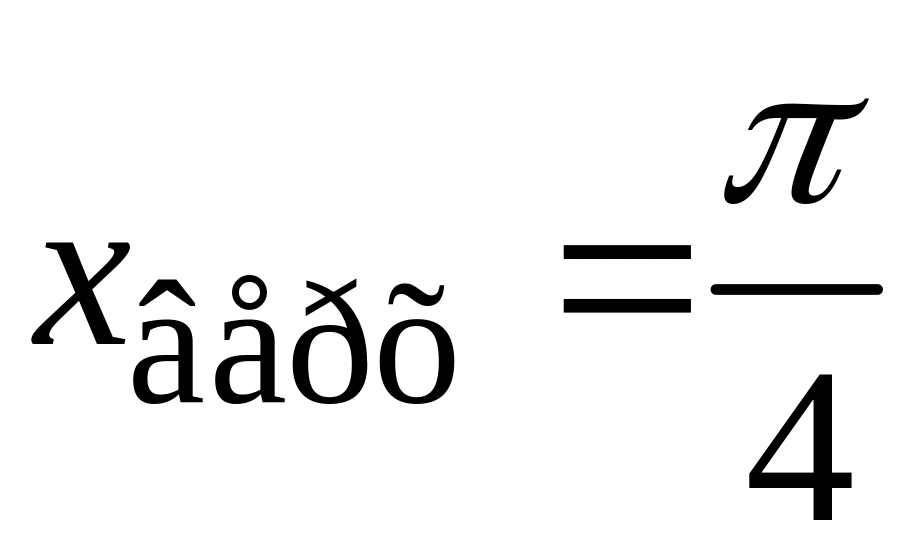 новая переменная интегрирования в
соответствии с заменой будет меняться
от
новая переменная интегрирования в
соответствии с заменой будет меняться
от
![]() до
до
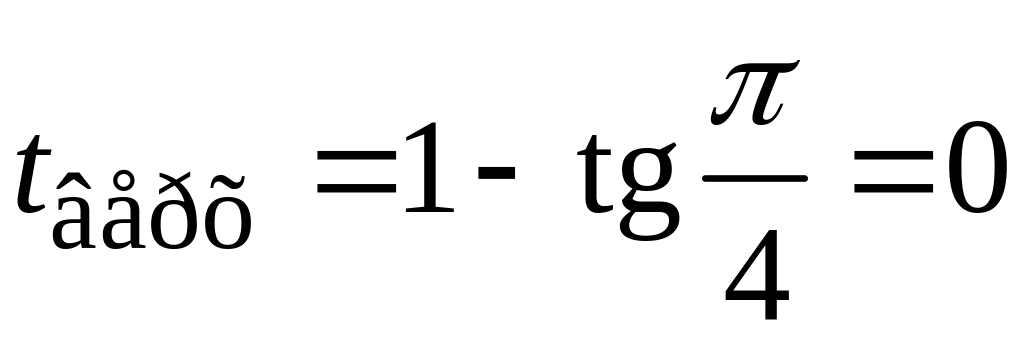 .
Во-вторых,
.
Во-вторых,
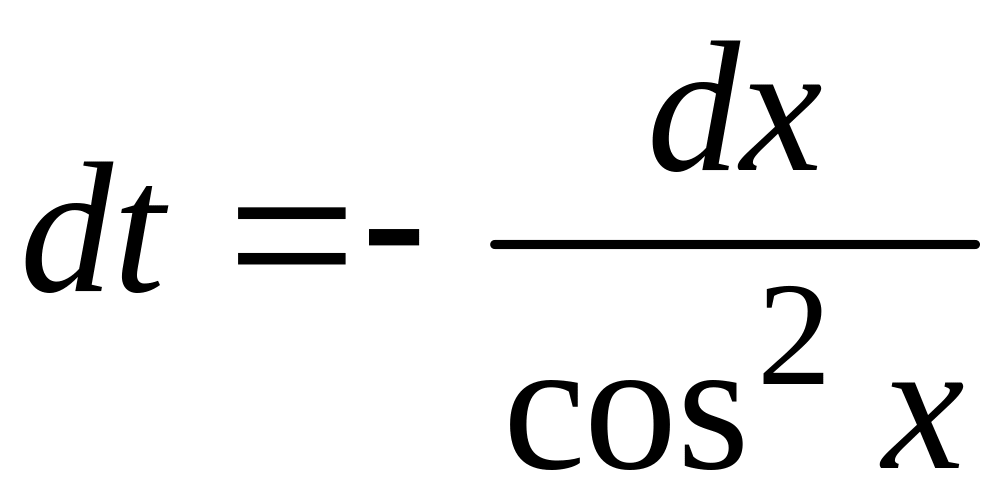 ,
то есть
,
то есть
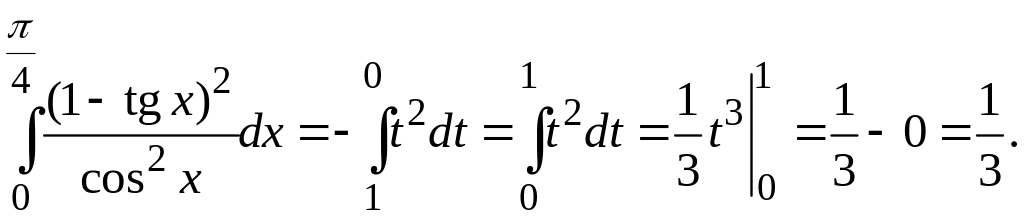
ПРИМЕР 3. Вычислить площадь фигуры, ограниченной линиями
![]() ;
;
![]() .
.
Решение.
1. Находим абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:
![]() =
=![]()
![]() .
.
 Отсюда
Отсюда
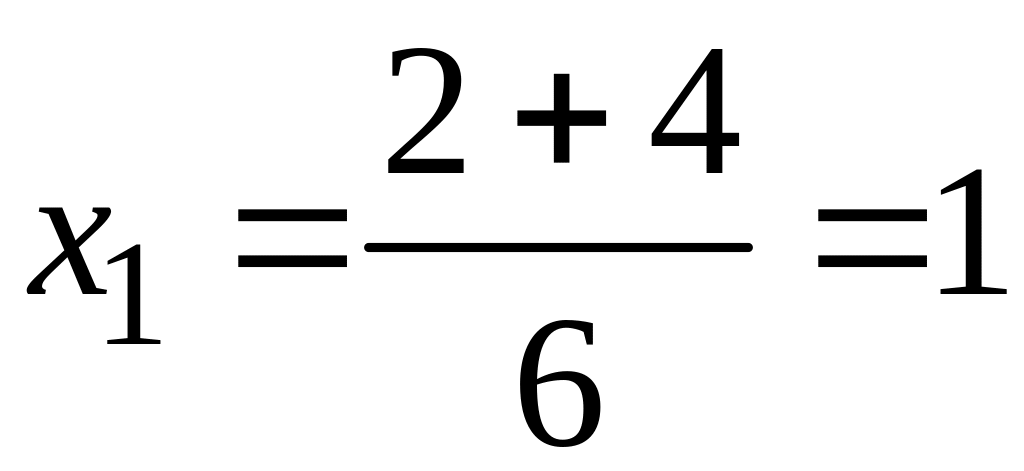 ,
,
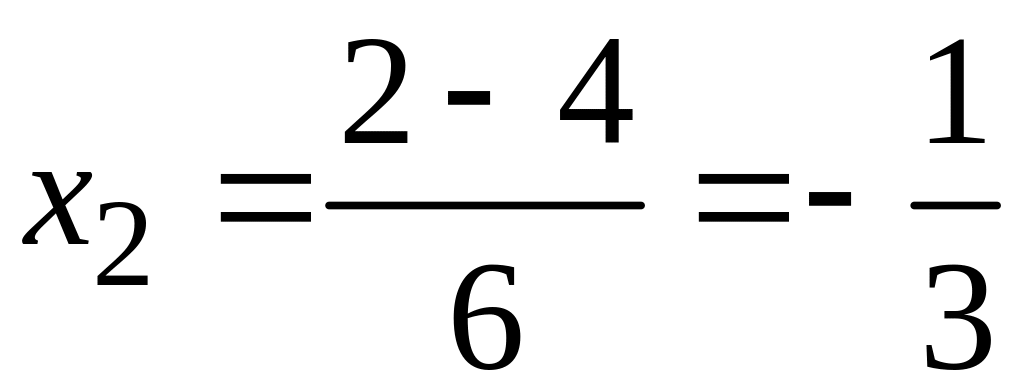 .
.
Далее
ищем ординаты точек пересечения
парабол
![]() ,
воспользовавшись, например, вторым
из заданных уравнений (
,
воспользовавшись, например, вторым
из заданных уравнений (![]()
 ),
и строим схематически искомую площадь
в системе координат.
),
и строим схематически искомую площадь
в системе координат.
2. Площадь фигуры вычисляем по формуле
 ,
,
где
![]() (
(![]() )
кривые, ограничивающие фигуру, а
)
кривые, ограничивающие фигуру, а
![]() отрезок
оси Ox,
в который она проектируется. В нашем
случае площадь равна
отрезок
оси Ox,
в который она проектируется. В нашем
случае площадь равна
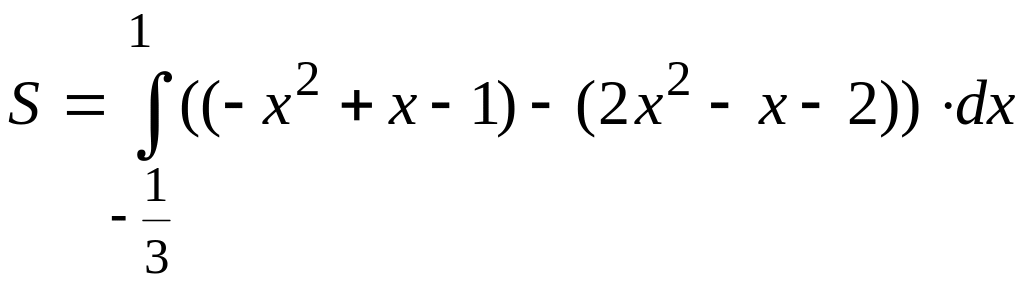 =
=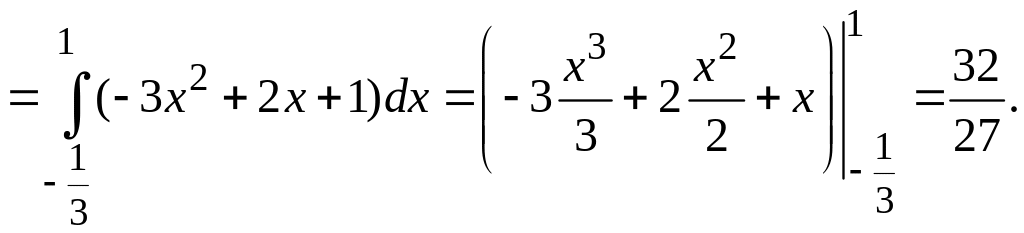
ПРИМЕР
4. Вычислить
объем тела, образованного вращением
вокруг оси Оx
фигуры, расположенной в первом квадранте
и ограниченной заданными параболой
![]() ,
прямой
,
прямой
![]() и осью Оx.
и осью Оx.
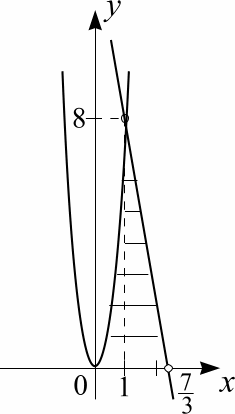 Решение.
Найдем абсциссу точки пересечения
параболы и прямой в первом квадранте.
Для этого решим уравнение
Решение.
Найдем абсциссу точки пересечения
параболы и прямой в первом квадранте.
Для этого решим уравнение
![]() =
=![]() ,
т.е.
,
т.е.
![]() .
Легко убедиться, что
.
Легко убедиться, что
![]() ,
,
![]() .
Первому квадранту соответствует корень
.
.
Первому квадранту соответствует корень
.
Найдем
теперь абсциссу точки пересечения
прямой с осью
![]() ,
решив уравнение
,
решив уравнение
![]() .
Получаем
.
Получаем
![]() .
.
Таким
образом, тело ограничено при
![]() поверхностью, образованной вращением
параболы
поверхностью, образованной вращением
параболы
![]() вокруг оси
,
а при
вокруг оси
,
а при
![]()
вращением прямой
.
вращением прямой
.
Искомый объем находим по формуле
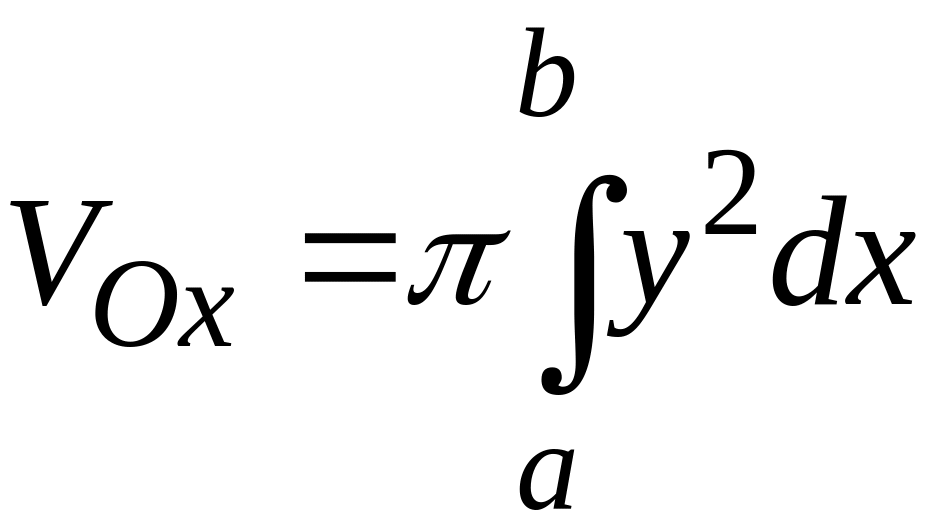 .
.
В нашем случае имеем
![]() +
+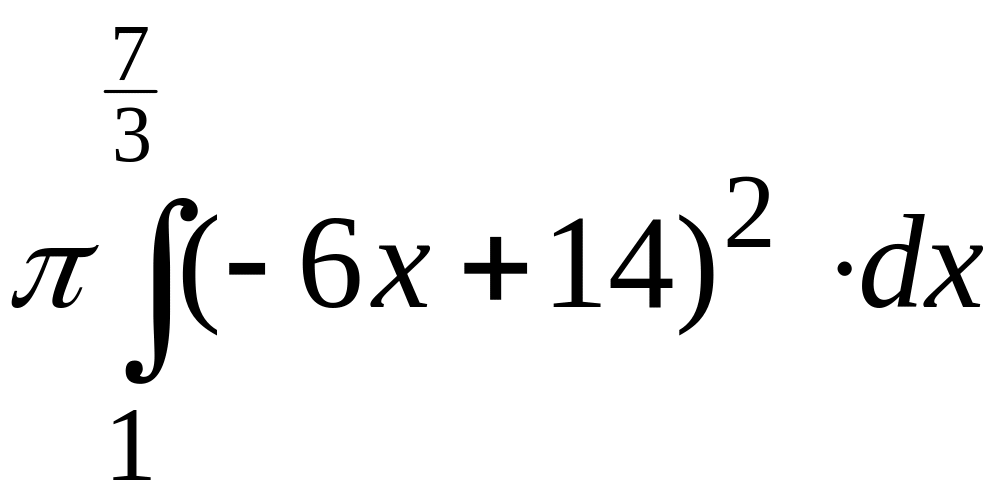 .
.
Первый интеграл вычисляется просто:
![]() =
=
=
=![]() =
=
=
=![]() .
.
Для
вычисления второго интеграла используем
подстановку
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
При этом из условия
.
При этом из условия
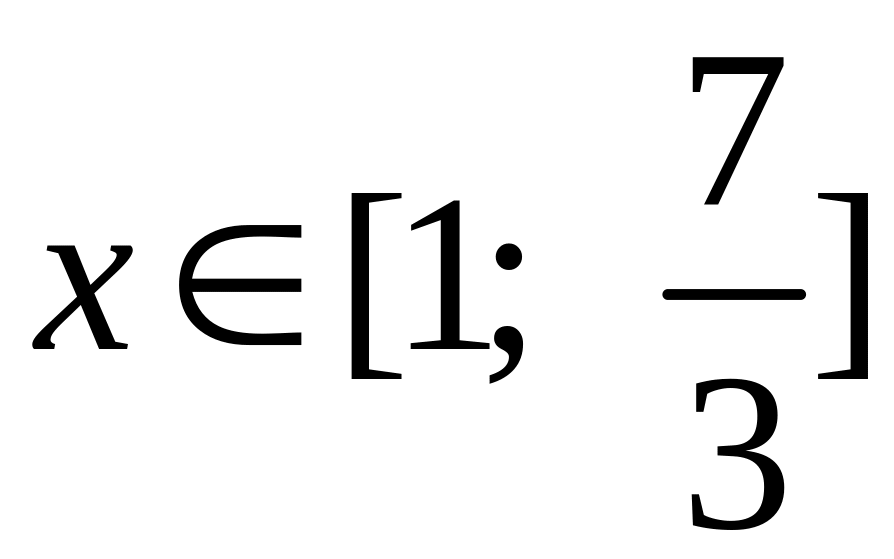 следует, что
следует, что
![]() меняется от 8 до 0 и
меняется от 8 до 0 и
=
![]() =
=![]() =
=![]() .
.
Следовательно,
![]() =
+
=
=
+
=![]() .
.
ПРИМЕР
5. Интеграл
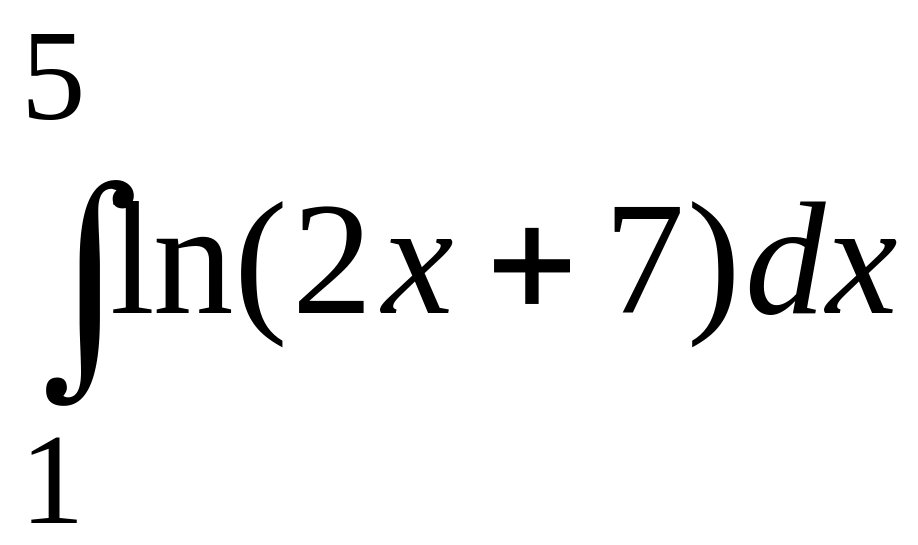 вычислить
приближенно по формуле трапеций, разбив
отрезок интегрирования на десять равных
частей. Оценить погрешность.
вычислить
приближенно по формуле трапеций, разбив
отрезок интегрирования на десять равных
частей. Оценить погрешность.
Решение.
1. Вычисляем интеграл приближенно по формуле трапеций
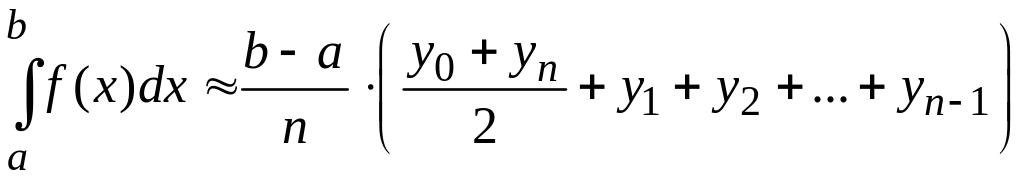 ,
,
разбивая
отрезок интегрирования
![]() на
n
= 10 равных частей. В нашем случае
на
n
= 10 равных частей. В нашем случае
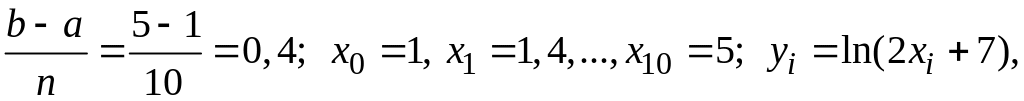
![]() ,
поэтому
,
поэтому
|
1 |
1,4 |
1,8 |
2,2 |
2,6 |
3 |
3,4 |
3,8 |
4,2 |
4,6 |
5 |
|
2,20 |
2,28 |
2,36 |
2,43 |
2,50 |
2,56 |
2,62 |
2,68 |
2,73 |
2,78 |
2,83 |
Теперь
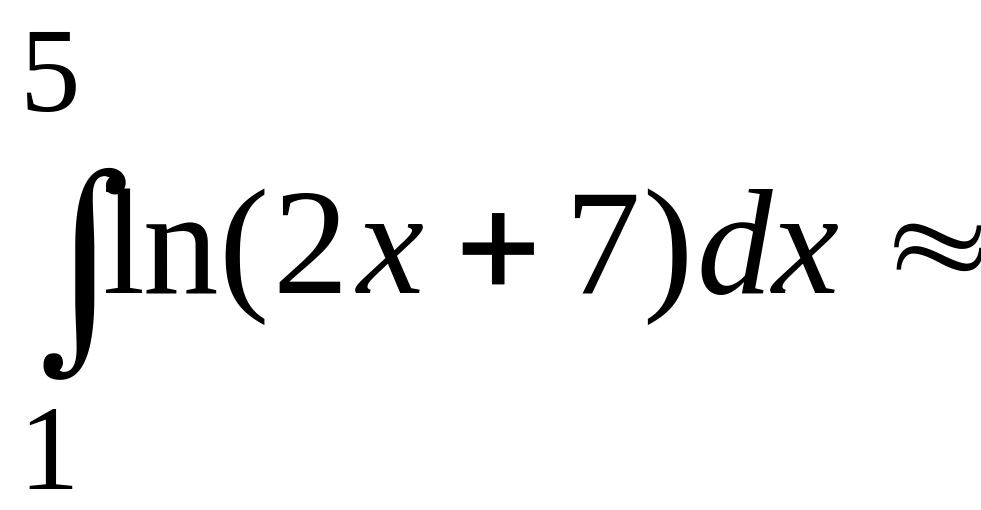
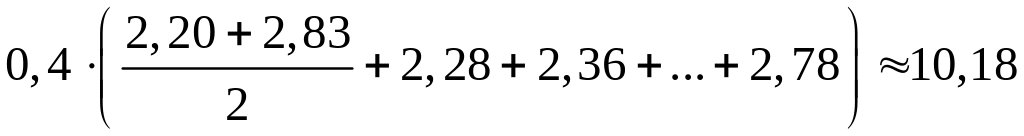 .
.
2. Приступаем к оценке абсолютной погрешности полученного результата по формуле
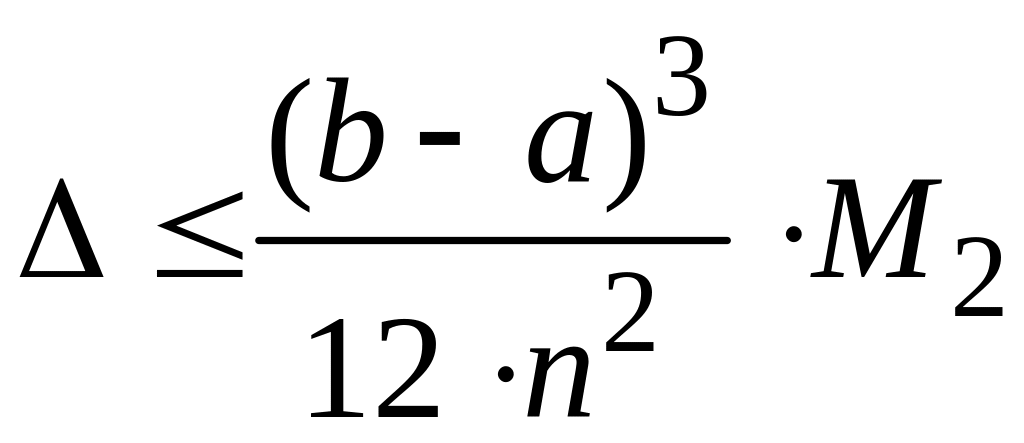 ,
,
где
a,
b
соответственно нижний и верхний пределы
интегрирования, n
число разбиений отрезка интегрирования
на части,
![]() ,
а
,
а
![]() подынтегральная
функция. В нашем случае имеем
подынтегральная
функция. В нашем случае имеем
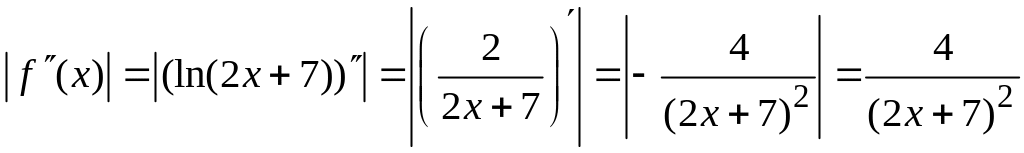 .
.
Функция
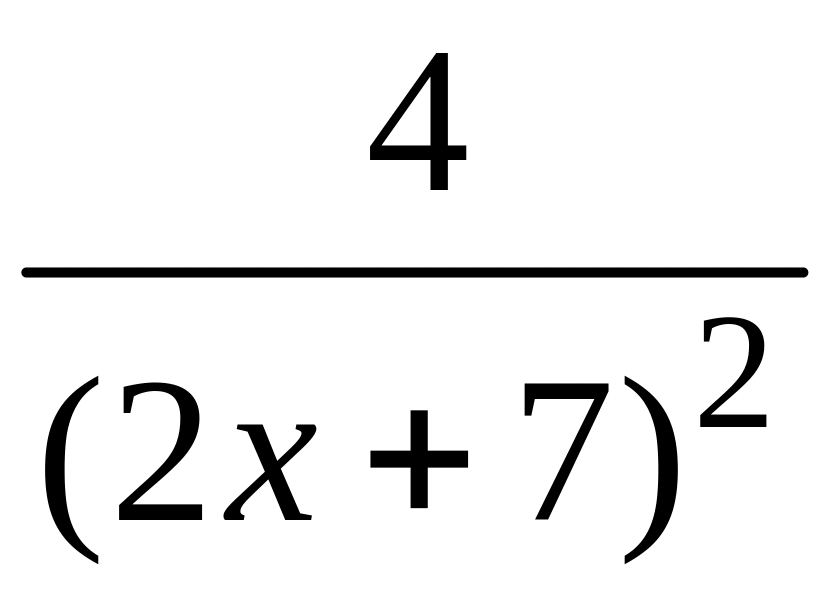 монотонно убывает на [1; 5], поэтому
достигает своего максимального значения
в левой концевой точке этого отрезка,
т.е. при
монотонно убывает на [1; 5], поэтому
достигает своего максимального значения
в левой концевой точке этого отрезка,
т.е. при
![]() .
Следовательно,
.
Следовательно,
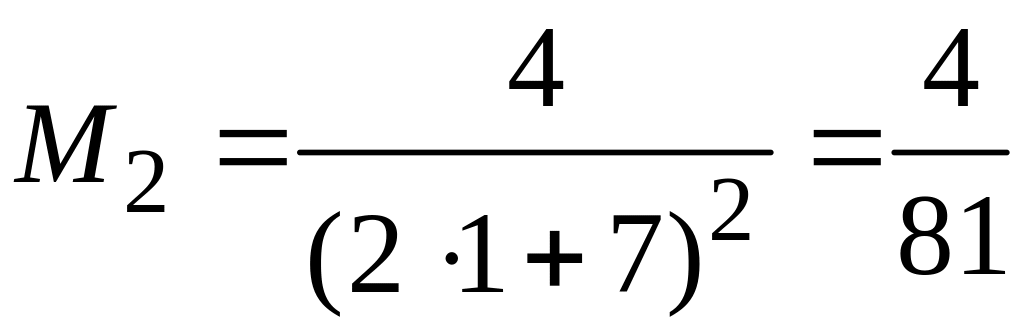 .
.
Таким
образом,
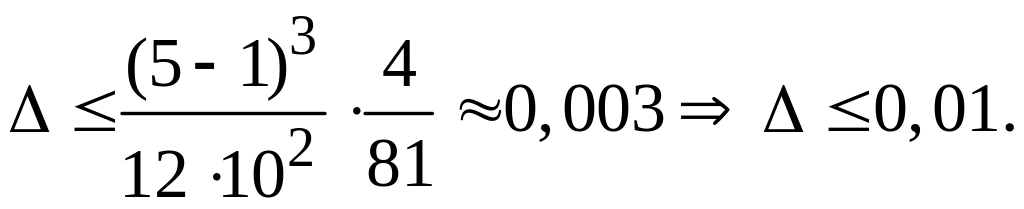
ТЕМА V. Дифференциальные уравнения
ВОПРОСЫ К ТЕМЕ
Понятие дифференциального уравнения, примеры. Дифференциальное уравнение первого порядка. Основные понятия. Задача Коши, теорема существования и единственности ее решения.
Простейшие типы дифференциальных уравнений первого порядка и способы их интегрирования.
Дифференциальные уравнения второго порядка, основные понятия.
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, теорема о структуре его общего решения.
Характеристическое уравнение. Отыскание уо.о. в случае различных ситуаций для корней характеристического уравнения.
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Теорема о структуре его общего решения.
Отыскание уч.н. для различных стандартных правых частей.
Моделирование свободных колебаний динамических систем.
Моделирование вынужденных колебаний динамических систем.
ТИПОВОЙ РАСЧЕТ 5
ЗАДАЧА 5.1. Для дифференциальных уравнений без начальных условий найти их общие решения. При наличии начальных условий найти соответствующие этим условиям частные решения.
Вариант 1.
1. xy2y1 = y2. |
2. x2dy+(y2+2)dx = 0. |
3. xyy = x3; y(1)=0. |
4. xyy = x2sin2x; y()=1. |
5. y7y+10y = 0; y(0)=2, y(0)= 1. |
6. y4y+3y = 0; y(0)=0, y(0)=1. |
7. y2y = 3x2+1. |
8. y+8y+16y = 3e2x. |
