
5066
.pdf
21
опорные оптимальные планы X 1 , X 2 , ..., X k и записать оптимальное решение в виде выпуклой линейной комбинации этих планов:
|
|
|
|
|
|
|
k |
|
X опт. t1 X 1 t2 X 2 ... tk X k , где t j 0, |
t j 1. |
|||||||
|
|
|
|
|
|
|
j |
1 |
Решить симплексным методом:
1. |
Z |
x1 |
max |
|
|
|
4x1 |
3x2 |
12, |
|
|
x1 |
x2 |
2, |
|
|
x1 |
x2 |
2, |
|
|
x1,2 |
0 . |
|
3. |
Z |
x1 |
2x2 |
max |
x1 x2 5, 2x1 6, x2 5,
x1,2 0.
5. |
Z |
x2 |
x3 |
max |
|
|
|
|
x1 |
x2 |
|
x3 |
|
1, |
|
|
|
x2 |
|
2x3 |
x4 |
2, |
|
|
x j |
0, j |
1,...,4. |
|
|
||
7. |
Z |
2x1 |
|
3x2 |
5x3 |
min |
|
|
2x1 |
x2 |
x3 |
|
4, |
|
|
|
x1 |
2x2 |
|
x4 |
12, |
|
|
|
x j |
0 , j 1,...,4. |
|
|
|||
9. |
Z |
x1 |
2x2 |
2x3 |
x4 |
max |
|
|
x1 |
x3 |
|
0.5x4 |
1, |
|
|
|
x2 x3 |
|
x4 |
1, |
|
||
|
x j |
0, |
j |
1,...,4. |
|
|
|
2. Z |
2x1 |
x2 |
3x3 2x4 |
x5 |
max |
|||
|
x1 |
x2 |
x3 |
|
1, |
|
||
|
x1 |
x2 |
|
x4 |
1, |
|
||
|
x1 |
x2 |
|
|
x5 |
1, |
|
|
|
x j |
0 , j |
1,...,5. |
|
|
|
||
4. Z |
4x1 |
2x2 |
max |
|
|
|
||
2x1 |
x2 |
14, |
|
|
|
|
||
|
x1 |
x2 |
10, |
|
|
|
|
|
|
x1 |
|
5, |
|
|
|
|
|
|
x1,2 |
0 . |
|
|
|
|
|
|
6. Z |
2x1 |
3x2 |
5x3 |
max |
|
|||
x1 |
x3 |
1, |
|
|
|
|
||
|
x2 |
x3 |
|
6, |
|
|
|
|
x j |
0, |
j |
1, 2, 3. |
|
|
|
||
8. Z |
x1 |
2x2 |
x3 |
2x4 |
|
x5 |
min |
|
x1 |
2x2 |
|
x3 |
|
|
2, |
|
|
2x1 |
x2 |
|
x4 |
|
0, |
|
||
x1 |
3x2 |
|
|
x5 |
|
6, |
|
|
x j |
0 , j |
1,...,5 . |
|
|
|
|||
10. Z |
x1 |
2x2 |
3x3 |
x4 |
2x5 |
min |
||
|
x1 |
3x2 |
|
4x3 |
|
|
6, |
|
|
|
2x2 |
|
5x3 |
x4 |
|
4, |
|
|
|
x2 |
|
2x3 |
x5 |
1, |
|
|
|
x j |
0, |
j |
1,...,5. |
|
|
|
|
22
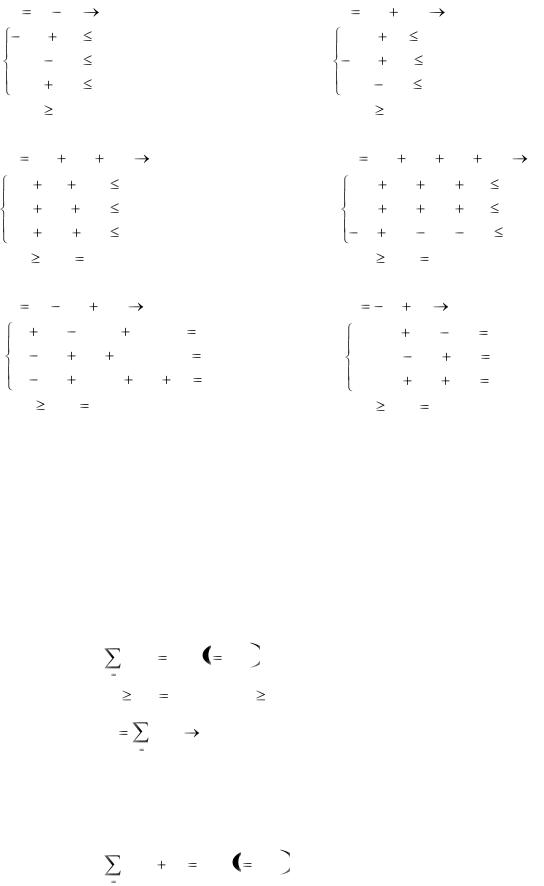
11. Z |
x1 |
x2 |
max |
|
|
12. Z |
2x1 |
2x2 |
max |
|
|
|||||
2x1 |
x2 |
2, |
|
|
|
x1 |
x2 |
5, |
|
|
|
|||||
x1 |
2x2 |
2, |
|
|
2x1 |
x2 |
2, |
|
|
|
||||||
x1 |
|
x2 |
5, |
|
|
|
|
x1 |
2x2 |
2, |
|
|
|
|||
x1,2 |
0. |
|
|
|
|
x1,2 |
0. |
|
|
|
|
|
|
|||
13. Z |
2x1 |
3x2 |
5x3 |
max |
|
14. Z |
2x1 |
3x2 |
6x3 |
3x4 |
max |
|||||
x1 |
|
x2 |
|
x3 |
3, |
|
|
2x1 |
x2 |
|
x3 |
x4 |
1, |
|||
2x1 |
|
3x2 |
x3 |
5, |
|
|
2x1 |
x2 |
|
x3 |
x4 |
2, |
||||
2x1 |
|
2x2 |
3x3 |
6, |
|
|
|
x1 |
4x2 |
2x3 |
2x4 |
3, |
||||
x j |
|
0, |
j |
1, 2, 3. |
|
|
|
x j |
0, |
j |
1,...,4. |
|
|
|||
15. Z |
x2 |
2x3 2x5 |
min |
|
16. Z |
x4 |
|
x5 |
|
max |
|
|
||||
x1 |
|
3x2 |
|
x3 |
2x5 |
7, |
|
x1 |
|
|
x4 |
2x5 |
1, |
|
||
|
|
2x2 |
|
4x3 |
x4 |
|
2, |
|
x2 |
|
|
2x4 |
x5 |
2, |
|
|
|
|
4x2 |
|
3x3 |
|
8x5 x6 |
6, |
|
|
x3 |
|
3x4 |
x5 |
3, |
|
|
x j |
|
0, |
j |
1,...,6. |
|
|
|
x j |
0, |
j |
1,...,5. |
|
|
|||
5. МЕТОД ИСКУССТВЕННОГО БАЗИСА (М-задача)
Метод искусственного базиса применяется при решении задач линейного программирования, системы ограничений которых не являются каноническими.
Рассмотрим задачу в общем виде:
n |
|
|
|
|
|
|
|
|
|
aij x j |
ai0 |
i 1, m , |
(1) |
||||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x j |
0( j |
1,n), |
|
ai0 |
0. |
|||
|
n |
|
|
|
|
|
|
|
Z |
c j x j |
max. |
(2) |
|||||
|
j 1 |
|
|
|
|
|
|
|
Пусть система (1) не является системой с базисом. Прибавим к левой части каждого уравнения системы (1) переменную уi ≥ 0, которую назовем искусственной. Система примет вид:
n
|
|
|
(3) |
aij x j yi ai 0 i 1, m . |
|||
j1
(3)– система с базисом.

23
Составим новую целевую функцию:
n |
|
m |
|
|
T |
c j x j M |
yi |
max. |
(4) |
j 1 |
|
i 1 |
|
|
Задача нахождения максимума функции (4) при ограничениях (3) называется М-задачей.
Замечание 1. Если исходная задача решается на минимум, то целевая функция М-задачи составляется так:
n |
m |
T |
c j x j M yi min. |
j 1 |
i 1 |
В обоих случаях М может принимать сколь угодно большое положительное значение.
Замечание 2. Искусственные неизвестные следует вводить только в те ограничения, которые не содержат базисных неизвестных.
Связь между решениями исходной и М-задачей устанавливается следующими теоремами.
Теорема 1. Если в оптимальном плане Y  1 , 2 ,..., n , 0,...,0
1 , 2 ,..., n , 0,...,0 М-задачи все искусственные переменные равны нулю, то соответствующее решение X
М-задачи все искусственные переменные равны нулю, то соответствующее решение X 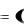 1 , 2 ,..., n
1 , 2 ,..., n  исходной задачи также является оптимальным.
исходной задачи также является оптимальным.
Теорема 2. Если в оптимальном плане М-задачи хотя бы одна из искусственных переменных отлична от нуля, то исходная задача решения не имеет.
Алгоритм метода искусственного базиса имеет свои особенности:
1)симплексная таблица имеет две оценочные строки: М-строку и Z- строку. Оценка в М-задаче имеет вид: а + bМ, где М > 0 сколь угодно большое число. Следовательно, знак оценки определяется знаком коэффициента b. Число а записываем в Z-строку (первую строку оценки), а коэффициент b – в М-строку (вторую строку);
2)разрешающий столбец выбирается по оценкам М-строки;
3)если все искусственные переменные вышли из базиса, задача решается дальше обычным симплекс-методом;
4)если М-задача решена, но искусственные переменные не вышли из базиса, то исходная задача решения не имеет.
24
Пример 1.
Z 5x1 |
2x2 x3 |
max |
||
2x1 |
x2 |
x3 |
5, |
|
3x1 |
2x2 |
x3 |
6, |
|
5x1 |
3x2 |
4x3 |
1, |
|
x j |
0, |
j |
1, 2, 3. |
|
Преобразуем систему ограничений к системе уравнений:
2x1 |
x2 |
x3 x4 |
5, |
3x1 |
2x2 |
x3 |
6, |
5x1 |
3x2 |
4x3 |
x5 1. |
Второе и третье ограничения не содержат базисных неизвестных, поэтому мы добавляем искусственные переменные именно в эти уравнения:
2x1 |
x2 |
x3 x4 |
|
5, |
3x1 |
2x2 |
x3 |
y1 |
6, |
5x1 |
3x2 |
4x3 |
x5 |
y2 1. |
Целевая функция М-задачи:
|
|
T 5x1 |
x2 |
x3 M y1 y2 |
max . |
|
|
|
|||
Составляем симплексную таблицу: |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Сj |
Б |
0 |
|
5 |
|
2 |
|
-1 |
0 |
0 |
θ |
ai 0 |
|
x1 |
|
x2 |
|
x3 |
x4 |
x5 |
|||
|
|
|
|
|
|
||||||
0 |
x4 |
5 |
|
2 |
|
1 |
|
1 |
1 |
0 |
5/2 |
M |
y1 |
6 |
|
3 |
|
2 |
|
1 |
0 |
0 |
2 |
M |
y2 |
1 |
|
5 |
|
3 |
|
4 |
0 |
-1 |
1/5 |
|
Z |
0 |
|
-5 |
|
-2 |
|
1 |
0 |
0 |
|
|
M |
-7 |
|
-8 |
|
-5 |
|
-5 |
0 |
1 |
|
0 |
x4 |
23/5 |
|
0 |
|
-1/5 |
|
-3/5 |
1 |
2/5 |
23/2 |
M |
y1 |
27/5 |
|
0 |
|
1/5 |
|
-7/5 |
0 |
3/5 |
27/3 |
5 |
x1 |
1/5 |
|
1 |
|
3/5 |
|
4/5 |
0 |
-1/5 |
- |
|
Z |
1 |
|
0 |
|
1 |
|
5 |
0 |
-1 |
|
|
M |
-27/5 |
|
0 |
|
-1/5 |
|
7/5 |
0 |
-3/5 |
|
0 |
x4 |
1 |
|
0 |
|
-1/3 |
|
1/5 |
1 |
0 |
|
0 |
x5 |
9 |
|
0 |
|
1/3 |
|
-7/5 |
0 |
1 |
|
5 |
x1 |
2 |
|
1 |
|
2/3 |
|
1/3 |
0 |
0 |
|
|
Z |
10 |
|
0 |
|
4/3 |
|
8/3 |
0 |
0 |
|
25
Оптимальный план: X îïò .  2, 0, 0 ,
2, 0, 0 ,
Zmax 10.
Замечание. Как только искусственные переменные выходят из базиса, элементы М-строки обращаются в ноль, и в дальнейшем М-строка из рассмотрения исключается.
Пример 2.
Z 2x1 3x2 max x1 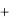 x2 1,
x2 1,
3x1 2x2 6,
x1,2 0.
Вводим балансовые переменные:
x1 |
x2 x3 |
1, |
3x1 |
2x2 |
x4 6. |
Система не каноническая. Составляем М-задачу:
T 2x1 3x2 My max
x1 |
x2 |
x3 |
1, |
3x1 |
2x2 |
x4 |
y 6, |
x j |
0, j |
1,...,4, |
|
y 0.
Решаем М-задачу симплексным методом:
Сj |
Б |
ai 0 |
2 |
3 |
0 |
0 |
θ |
|
x1 |
x2 |
x3 |
x4 |
|||||
|
|
|
|
|||||
0 |
x3 |
1 |
1 |
1 |
1 |
0 |
1 |
|
M |
y |
6 |
3 |
2 |
0 |
-1 |
2 |
|
|
Z |
0 |
-2 |
-3 |
0 |
0 |
|
|
|
M |
-6 |
-3 |
-2 |
0 |
1 |
|
|
2 |
x1 |
1 |
1 |
1 |
1 |
0 |
|
|
M |
y |
3 |
0 |
-1 |
-3 |
-1 |
|
|
|
Z |
2 |
0 |
-1 |
2 |
0 |
|
|
|
M |
-3 |
0 |
1 |
3 |
1 |
|
М-задача решена (нет отрицательных оценок в М-строке), но в этом решении искусственная неизвестная y осталась в базисе, следовательно,

26
исходная задача не имеет оптимального решения, так как область допустимых решений этой задачи пустая.
Решить следующие задачи:
1. |
Z |
x1 |
x2 |
max |
|
2x1 |
x2 |
2, |
|
|
|
x1 |
2x2 |
2, |
|
|
x1 |
x2 |
5, |
|
|
x1,2 |
0. |
|
3. |
Z |
x1 |
2x2 |
min |
x1 x2 8, x1 x2 2,
x1,2 0.
5. |
Z |
3x1 |
x2 |
x3 |
max |
|
|
2x1 |
|
x2 |
x3 |
2, |
|
|
x1 |
2x2 |
|
8, |
|
|
|
x1 |
|
x2 |
|
5, |
|
|
x j |
0, |
j |
1, 2, 3. |
|
|
7. |
Z |
4x1 |
2x2 |
x3 |
min |
|
|
x1 |
|
3x2 |
x3 |
4, |
|
|
|
|
2x2 |
x3 |
1, |
|
|
x j |
0, |
j 1, 2, 3. |
|
||
9. |
Z |
x1 |
2x2 |
min |
|
|
x1 x2 8, x1 x2 2, x1 3,
x1,2 0.
11. Z 2x1 3x2 |
min |
3x1 2x2 6, x1 4x2 4,
x1,2 0.
2. Z |
3x1 |
x2 3x3 |
34x4 min |
|
x1 |
2x2 |
x3 |
x4 |
0, |
2x1 |
2x2 |
3x3 3x4 |
9, |
|
x1 |
x2 |
2x3 |
x4 |
6, |
x j |
0, j |
1,...,4. |
|
|
4. Z |
x1 |
max |
|
|
x1 2x2 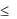 0, x1
0, x1  x2
x2 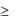 1, x1
1, x1 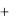 x2
x2 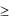 1,
1,
x1,2 0.
6. Z x1 2x2 max
|
x1 |
x2 |
1, |
|
|
|
|
x1 |
x2 |
5, |
|
|
|
|
x1 |
|
|
1, |
|
|
|
x1,2 |
0. |
|
|
|
|
8. Z |
2x1 |
2x2 |
3x3 |
max |
||
x1 |
x2 |
2x3 |
1, |
|
||
|
2x2 |
3x3 |
8, |
|
||
x j |
0, |
j |
1, 2, 3. |
|
||
10. Z |
x1 |
2x2 |
|
x3 |
max |
|
|
x1 |
x2 |
2x3 |
4, |
||
|
x1 |
2x2 |
|
|
3, |
|
|
x1 |
4x2 |
|
|
3, |
|
|
x j |
0, |
j |
1, 2, 3. |
||
12. Z |
x1 |
4x2 |
x3 |
max |
||
|
x1 |
x2 |
x3 |
14, |
||
2x1 |
5x2 |
x3 |
0, |
|||
|
x j |
0, |
j |
1, 2, 3. |
||
27
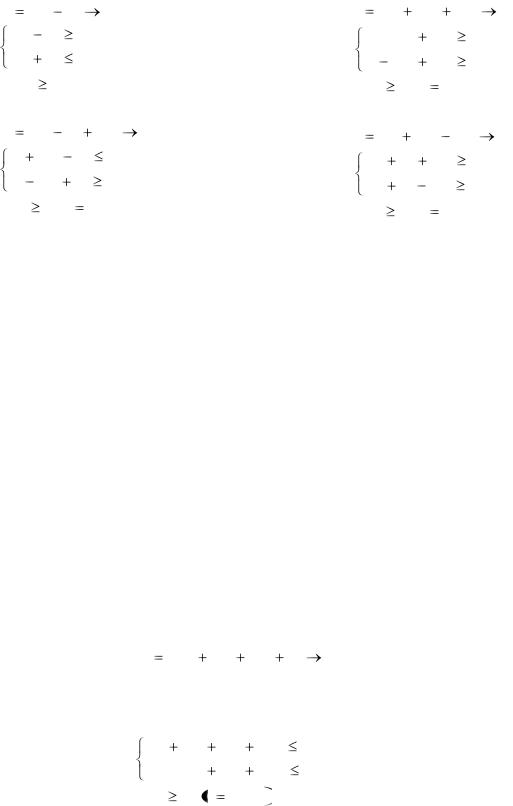
13. Z 2x1 x2 max |
14. |
2x1 x2 1, x1 x2 4,
x1,2 0.
15. Z |
2x1 |
x2 |
5x3 |
min |
16. |
x1 |
x2 |
x3 |
4, |
|
|
x1 |
5x2 |
x3 |
5, |
|
|
x j |
0, |
j 1, 2, 3. |
|
|
|
Z 6x1 4x2 4x3 min x1  x2 2x3 1,
x2 2x3 1,
x1 2x2 2x3 6,
x j |
0, j 1, 2, 3. |
Z 3x1 2x2 4x3 min x1 x2 2x3 4,
3x1 x2 4x3 7,
x j |
0, j 1, 2, 3. |
6. ДВОЙСТВЕННОСТЬ
Пример 1. Рассмотрим задачу об оптимальном плане выпуска продукции: для изготовления 4 видов продукции используется 2 вида сырья. Запасы сырья и его расход на изготовление единицы каждого вида продукции даны в таблице:
Виды сырья |
|
Запасы |
|
Виды продукции |
|
||
|
I |
II |
III |
|
IV |
||
|
|
|
|
||||
А |
|
160 |
4 |
3 |
1 |
|
1 |
Б |
|
900 |
- |
4 |
9 |
|
12 |
Доход |
|
12 |
5 |
4 |
|
1 |
|
|
|
|
|
|
|
|
|
Определить оптимальный план выпуска продукции из условия максимизации прибыли.
Математическая формулировка (модель) задачи: Максимизировать функцию
Z |
12x1 |
5x2 |
4x3 |
x4 max, |
||
при ограничениях |
|
|
|
|
|
|
4x1 |
3x2 |
x3 |
x4 |
160, |
|
y1 |
|
||||||
|
4x2 |
9x3 |
12x4 |
900, |
|
y2 |
x j |
0 |
j 1,...,4 . |
|
|
|
|
Предположим, что некоторая организация желает приобрести сырье, которым располагает предприятие. Надо оценить каждую единицу, используемых ресурсов. Будем такую оценку условно называть ценой.
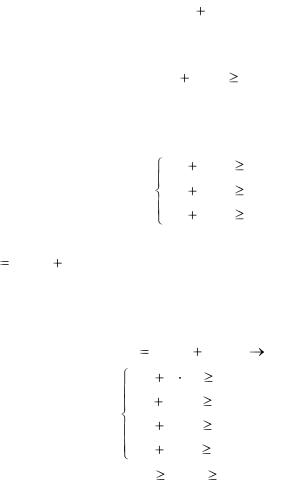
28
Обозначим соответственно, через y1 и y2 цену единицы сырья А и Б. Производство продукции вида I приносит предприятию доход 12
денежных единиц. При этом расходуется 4 единицы сырья А и 0 единиц сырья Б. Выручка от продажи сырья, расходуемого на единицу продукции I по ценам y1 и y2 , составит
4 y1 0  y2 .
y2 .
Эта величина должна быть не меньше тех доходов, которые предприятие получит от реализации продукции вида I, следовательно,
4 y1 0  y2 12.
y2 12.
Аналогичные рассуждения в отношении единицы продукции вида II, III, IV приводят к следующим неравенствам:
3y1 |
4 |
y2 |
5, |
|
y1 |
9 |
y |
2 |
4, |
y1 |
12y |
2 |
1. |
|
Общая стоимость всех запасов сырья, приобретаемого организацией, составит W 160y1 900y2 .
Покупатель будет стремиться купить сырье как можно дешевле, т.е. минимизировать функцию W .
Получим задачу:
W |
160y1 |
900y2 |
|
min |
4 y1 |
0 y2 |
12, |
|
x1 |
|
||||
3y1 |
4 y2 |
5, |
|
x2 |
y1 |
9 y2 |
4, |
|
x3 |
y1 |
12y2 |
1, |
|
x4 |
y1 |
0, y2 |
0. |
|
|
Получили задачу, двойственную данной. Следовательно, для стандартной задачи нужно выполнить следующие действия, для того чтобы получить ей двойственную:
1)число неизвестных в двойственной задаче равно числу ограничений в исходной;
2)неравенства в системе ограничений двойственной задачи будут противоположного смысла, чем неравенства в системе ограничений исходной задачи; сохраняется неотрицательность переменных;
3)свободные члены ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи, а коэффициенты целевой функции исходной задачи превращаются в свободные члены двойственной задачи;
4)в исходной задаче целевая функция минимизируется, а в двойственной – максимизируется.

29
По решению одной из задач можно сразу определить решение другой.
Решим исходную задачу симплекс-методом:
Сj |
Б |
0 |
12 |
5 |
4 |
1 |
0 |
0 |
θ |
|
ai 0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
||||
|
|
|
||||||||
0 |
x5 |
160 |
4 |
3 |
1 |
1 |
1 |
0 |
40 |
|
0 |
x6 |
900 |
0 |
4 |
9 |
12 |
0 |
1 |
- |
|
|
Z = |
0 |
-12 |
-5 |
-4 |
-1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
x1 |
40 |
1 |
3/4 |
1/4 |
1/4 |
1/4 |
0 |
160 |
|
0 |
x6 |
900 |
0 |
4 |
9 |
12 |
0 |
1 |
100 |
|
|
Z = |
480 |
0 |
4 |
-1 |
2 |
3 |
0 |
|
|
12 |
x1 |
15 |
1 |
23/36 |
0 |
-1/12 |
1/4 |
-1/36 |
|
|
4 |
x3 |
100 |
0 |
4/9 |
1 |
4/3 |
0 |
1/9 |
|
|
|
Z = |
580 |
0 |
40/9 |
0 |
10/3 |
3 |
1/9 |
|
|
|
|
|
|
|
|
|
y1 |
y2 |
|
|
|
|
|
|
15, 0,100,0 . |
Zmax 580 ден. ед.при X |
|||||
Следовательно, для двойственной задачи |
|
||||
|
|
|
3,1/9 . |
||
Wmin 580 ед.при Y |
|||||
Неизвестные в двойственной задаче равны соответствующим оптимальным оценкам базисных переменных исходной задачи плюс коэффициент, стоящий в таблице над соответствующей базисной
переменной (Сj), т.е. y1 |
3 0 |
3; y2 |
1/ 9 |
0 |
1/ 9 . |
Проверим: |
|
|
|
|
|
|
W 160y1 |
900y2 |
min . |
||
При y1 3, y2 1/ 9 , Wmin |
160 3 |
900 1/ 9 |
480 |
100 580 . |
|
Пример 2. В двойственной задаче к основной переменные могут иметь любой знак. Составим двойственную задачу к основной:
Z 3x1 x2 x3 max
2x1 |
x2 |
x3 |
6, |
y1 |
x1 |
2x2 |
x3 |
4, |
y2 |
x j |
0, j |
1, 2, 3. |
|
|
30
Двойственная задача имеет следующий вид:
W 6 y1 4 y2 min
2 y1 |
y |
2 |
3, |
x1 |
y1 |
2 y |
2 |
1, |
x2 |
y1 |
y2 |
1. |
x3 |
|
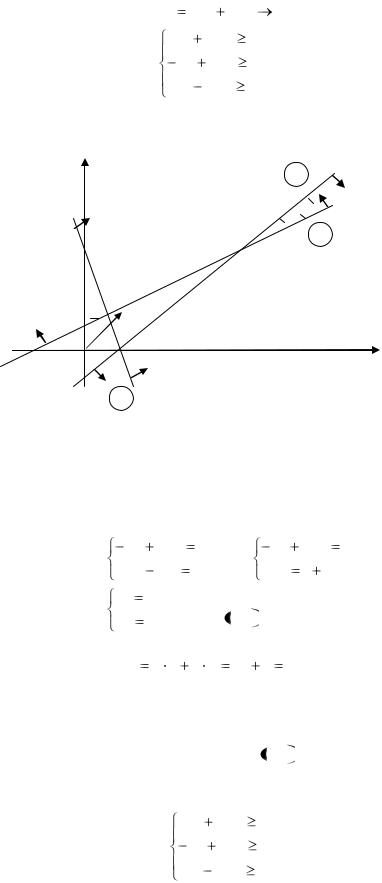
Решим двойственную задачу графически
y2 |
3 |
|
|
А |
2 |
n
y1
1
Координаты точки А дают значения неизвестных y1 и y2 , при которых функция W принимает минимальное значение.
Найдем координаты этой точки:
y1 |
2 y2 |
3, |
y1 |
2 y2 3, |
y1 |
y2 |
1, |
y1 |
1 y2 , |
y1 |
3, |
|
|
|
y2 |
2, |
A |
3, 2 , |
|
Wmin |
6 3 |
4 2 |
18 8 |
26. |
По решению двойственной задачи найдем решение исходной по второй
теореме двойственности (теореме равновесия). |
|
||
Подставим координаты точки |
|
A 3, 2 |
в систему ограничений |
двойственной задачи: |
|
|
|
2 y1 |
y2 |
3, |
|
y1 |
2 y2 |
1, |
|
y1 |
y2 |
1. |
|
