636_Nosov_V.I._Seti_radiodostupa_CH.1_

Полученный результат подтверждает, что принятое кодовое слово содержит ошибку (введенную нами), поскольку S ≠ 0.

Локализация ошибки

Допустим, в кодовом слове имеется ошибок, расположенных на позициях X j1 , X j2 ,..., X j . Тогда полином ошибок, определяемый уравнениями (4.50) и (4.51), можно записать следующим образом

расположение ошибки. Для коррекции искаженного кодового слова нужно

У нас имеется 2t неизвестных (t значений ошибок и t расположений) и система 2t уравнений. Впрочем, эту систему 2t уравнений нельзя решить обычным путем, поскольку уравнения в ней нелинейные (некоторые неизвестные входят в уравнение в степени). Методика, позволяющая решить эту систему уравнений, называется алгоритмом декодирования кода Рида-Соломона.

Если вычислен ненулевой вектор синдрома (один или более его символов не равны нулю), это означает, что в принятом кодовом слове Z(X) есть ошибка (ошибки). Далее нужно узнать расположение ошибки (или ошибок). Полином локатора ошибок можно определить следующим образом

141

Корнями (Х) будут 1 , 1 ,..., 1 . Величины, обратные корням (Х) ,

1 2

будут представлять номера расположений моделей ошибки E(Х). Тогда, воспользовавшись авторегрессионной техникой моделирования [5], мы составим из синдромов матрицу, в которой первые t синдромов будут использоваться для предсказания следующего синдрома

Воспользуемся авторегрессионной моделью уравнения (4.63), взяв матрицу наибольшей размерности с ненулевым определителем. Для кода (7, 3) с коррекцией двухсимвольных ошибок матрица будет иметь размерность 2 2, и модель запишется следующим образом (4.64)

Чтобы найти коэффициенты 1 и 2 полинома локатора ошибок (Х), сначала необходимо вычислить обратную матрицу для уравнения (4.65). Обратная матрица для матрицы [А] определяется следующим образом

142

данном примере) l и l' обозначают 1-ю и 2-ю ошибки. Поскольку мы имеем дело с 2-символьными ошибками, полином ошибок можно записать следующим образом (4.73)

индексация номеров расположения ошибок является сугубо произвольной. Итак, в этом примере мы обозначили величины

ошибки, а индекс l – l-ю ошибку. Поскольку каждое значение ошибки связано с конкретным месторасположением, систему обозначений можно упростить,

любое из четырех синдромных уравнений. Выразим из уравнения (4.61) S1 и

S2

144

Чтобы найти значения ошибок E1 и E2 нужно определить обратную матрицу для уравнения (4.76)

Теперь мы можем найти из уравнения (4.76) значения ошибок

Исправление принятого полинома Z(X) с помощью найденного полинома ошибок E(X)

145

Показанный алгоритм восстанавливает принятый полином Z(X), выдавая

декодированное сообщение.

Поскольку символы сообщения содержатся в крайних правых k = 3 символах, декодировано будет следующее сообщение

Это сообщение в точности соответствует тому, которое было выбрано для этого примера (смотри уравнение (4.44)).

Эффективность кодирования – это снижение необходимого отношения Eb/N0 для системы с кодированием по сравнению с системой без кодирования (при одном и том же виде модуляции) для достижения заданной вероятности ошибок. Часто этот параметр называют энергетическим выигрышем кода – ЭВК.

В таблице 4.11 приведены значения ЭВК для некоторых блочных кодов при использовании в гауссовом канале модуляции BPSK, вероятности ошибки 10-5 при отношении Eb/N0.= 9,6 дБ без использования кодирования.

Таблица 4.11 Значения ЭВК блочных кодов

В таблице 4.12 приведены значения требуемого отношения Eb/N0 для блочного кода Рида-Соломона при использовании в гауссовом канале модуляции 32-MFSK с возможностью коррекции t символов и n = 31.

147

5. СВЕРТОЧНЫЕ КОДЫ

Блочные коды являются одним из двух видов кодов с коррекцией ошибок, широко используемых при беспроводной передаче. Второй вид – это сверточные коды. Блочный код (п, k) обрабатывает данные блоками по k бит, генерируя на выходе блок из п бит (п > k) для каждого k -битовго блока на входе. Если прием и передача данных происходят относительно непрерывным потоком то блочный код (в частности, с большим значением п) может быть не так удобен как код, который генерирует избыточные биты непрерывно. В последнем случае обнаружение и исправление ошибок выполняется непрерывно, и именно в этом состоит преимущество сверточных кодов[8, 17, 18, 21].

Сверточный код задается тремя параметрами: п, k и К. Код (п, k, К) обрабатывает входящие данные порциями по k бит и генерирует выходную последовательность, состоящую из п бит для каждых k бит входа. До этого момента принципы работы сверточных и блочных кодов не отличаются. Для сверточных кодов п и k, как правило, являются очень малыми числами. Разница между двумя типами кодов состоит в том, что сверточные коды используют память, которая характеризуется длиной кодового ограничения К. По сути, текущая п – битовая входная последовательность кода (п, k, К) зависит не только от значений текущего входного блока, состоящего из k бит, но также и от предыдущих (К -1) k - битовых блоков. Следовательно, текущая выходная п -битовая последовательность является функцией последних (K k) входных битов.

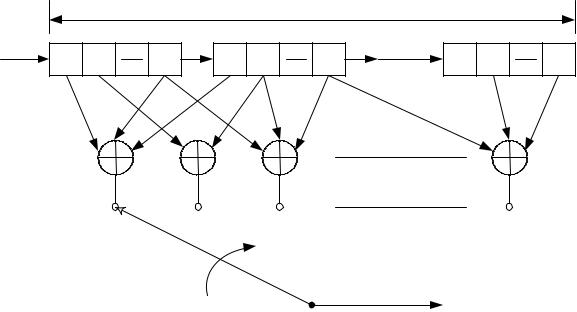
Свѐрточный код создаѐтся прохождением передаваемой информационной последовательности через линейный сдвиговый регистр с конечным числом состояний. В общем, регистр сдвига состоит из К (k -битовых) ячеек и линейного преобразователя, состоящего из п функциональных генераторов и выполняющего алгебраические функции как показано на рисунке. 5.1.

Входные данные к кодеру, которые считаются двоичными, продвигаются вдоль регистра сдвига по k бит за раз. Число выходных битов для каждой k - битовой входной последовательности равно п. Следовательно, кодовая скорость, определѐнная как Rc = k/n, согласуется с определением скорости блочного кода. Параметр К называется длиной кодового ограничения (или кодовым ограничением) свѐрточного кода и указывает число разрядов в регистре сдвига.

5.1 Представление сверточного кодера

Чтобы иметь возможность описывать сверточный код, необходимо определить кодирующую функцию G(m) так, чтобы по данной входной последовательности m можно было быстро вычислить выходную последовательность U. Для реализации сверточного кодирования используется несколько методов; наиболее распространенными из них являются графическая

148

связь, векторы, полиномы связи, диаграмма состояния, древовидная и решетчатая диаграммы. Все они рассматриваются ниже.

Kk ячеек

Кодированная последовательность

Рис. 5.1 Сверточный кодер

Представление связи

При обсуждении сверточных кодеров в качестве модели будем использовать сверточный кодер, показанный на рисунке 5.2, а. На этом рисунке изображен сверточный кодер (2, 1, 3) с длиной кодового ограничения К = 3. В нем имеется п =2 сумматора по модулю 2; следовательно, скорость кодирования кода k/n равна 1/2. При каждом поступлении входной бит помещается в крайний левый разряд, а биты регистра смещаются на одну позицию вправо. Затем коммутатор на выходе дискретизирует выходы всех сумматоров по модулю 2 (т.е. сначала верхний сумматор, затем нижний), в результате чего формируются пары кодовых символов, образующих кодовое слово, связанное с только что поступившим битом. Это выполняется для каждого входного бита. На рисунке 5.2, б представлена схема сверточного кодера с параметрами (3, 2, 2).

Выбор связи между сумматорами и разрядами регистра влияет на характеристики кода. Всякое изменение в выборе связей приводит в результате к различным кодам. Связь, конечно же, выбирается и изменяется не произвольным образом. Задача выбора связей, дающая оптимальные дистанционные свойства, сложна и в общем случае не решается; однако для всех значений длины кодового ограничения, меньших 20, с помощью компьютеров были найдены хорошие коды [18].

В отличие от блочных кодов, имеющих фиксированную длину слова п, в сверточных кодах нет определенного размера блока.

149

Рис. 5.2 Сверточный кодер (2, 1, 3) а) и (3, 2, 2) б)

Один из способов реализации кодера заключается в определении п векторов связи, по одному на каждый из п сумматоров по модулю 2. Каждый вектор имеет размерность К и описывает связь регистра сдвига кодера с соответствующим сумматором по модулю 2. Единица на i-й позиции вектора указывает на то, что соответствующий разряд в регистре сдвига связан с сумматором по модулю 2, а нуль в данной позиции указывает, что связи между разрядом регистра и сумматором по модулю 2 не существует Для кодера на рисунке 5.2,а можно записать вектор связи (генераторный полином) g1 для верхних связей, a g2 – для нижних

Аналогичным образом можно записать генераторные полиномы для кодера на рис. 5.2, б, учитывая, что в этом кодере каждый раз два бита поступают на вход регистров сдвига, а на выходе генерируется три бита