
557_Obrabotka_informatsii_i_matematicheskoe_modelirovanie_2014_
.pdf
Литература
1.Testing goodness-of-fit of parametric AFT and PH models with residuals. / N. Balakrishnan, E. Chimitova, N. Galanova, M. Vedernikova // Communications in Statistics – Simulation and Computation. – 2013. – vol. 42, no. 6. – pp. 1352-1367.
2.Применение непараметрических критериев согласия к проверке адекватности моделей ускоренных испытаний / Галанова Н.С., Лемешко Б.Ю., Чимитова Е.В. // Автометрия, Т.48, №6 – С. 53-68 – Новосибирск, 2012г.
3.Accelerated Life Models. Modeling and Statistical Analysis / Bagdonavicius V., Nikulin M. // Chapman&Hall/CRC, 2002. 360 p.
4.Statistical Models and Methods for Lifetime Data / J.F. Lawless. – New Jersey: Wiley-Interscience, 2002. – 664 p.
ПОСТРОЕНИЕ ОСТОВНОГО ДЕРЕВА НА ТРЕУГОЛЬНЫХ ВЕКТОРНЫХ ЭЛЕМЕНТАХ ДЛЯ МОДЕЛИРОВАНИЯ МАГНИТНОГО ПОЛЯ
Домников П.А. НГТУ, Новосибирск
e-mail: p_domnikov@mail.ru, тел.: (383) 346-27-76
При расчетах двумерных магнитных полей с использованием векторного метода конечных элементов [1] решается векторное дифференциальное уравнение
|
|
|
rot |
1 |
rot A J . |
(1) |
|
|
|
|
|||
|
|
|
|
|
|
|
Соответствующая вариационная постановка имеет вид |
|
|||||
|
1 |
rot A rot d J d , |
(2) |
|||
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
где пробная вектор-функция |
H0 (rot ) . Дискретизация |
вариационной |
||||
постановки (2) приводит к следующей системе линейных алгебраических уравнений (СЛАУ)
Bq f , |
(3) |
где элементы конечноэлементной матрицы жесткости B определяются |
|
соотношением |
|
[B]ij rot i rot j d . |
(4) |
|
|
При использовании реберных векторных базисных функций матрица жесткости B имеет вырожденное ядро, состоящее из градиентных функций, ассоциированных с узлами конечноэлементной сетки. Для устранения данного вырожденного ядра существует метод деревьев-кодеревьев [2], в
31
котором из конечноэлементного базиса исключаются реберные функции, входящее в остовное дерево.
В [3] был предложен такой способ построения остовного дерева на регулярной прямоугольной сетке, который приводит к невырожденной трехдиагональной матрице жесткости. Однако при решении задач в областях сложной геометрической формы использование треугольных конечных элементов является более универсальным. Поэтому в данной работе был разработан алгоритм построения остовного дерева на нерегулярных треугольных сетках. При разработке данного алгоритма преследовалась цель получить такую конечноэлементную матрицу жесткости, ненулевые элементы которой были бы расположены как можно ближе к главной диагонали.
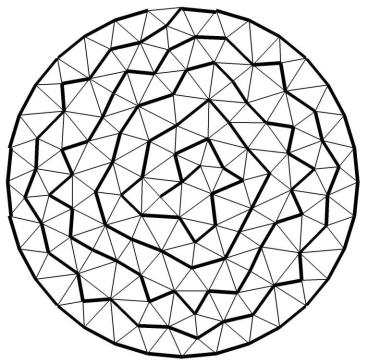
Разработанный алгоритм состоит из следующих шагов. Первым шагом строится остовное дерево по границе области. Затем в дерево включаются вершины и ребра внутри расчетной области, причем на каждом шаге в дерево включается первая непосещенная вершина (и соответствующее ей ребро) в порядке против часовой стрелки от текущей вершины. Посещенные вершины помещаются в стек. Если все соседи текущей вершины посещены, то следующая вершина достается из стека. После построения дерева нумеруются ребра кодерева, начиная с ребра, лежащего на границе области. Дальнейшая нумерация ребер происходит по элементам: сначала на текущем элементе нумеруются ребра кодерева в порядке против часовой стрелки, затем осуществляется переход в следующий элемент. Такой порядок обхода выбран для того, чтобы уменьшить расстояние ненулевых элементов матрицы до главной диагонали. Пример остовного дерева, полученного с использованием предложенного алгоритма, показан на рис.1. Для построения триангуляций был использован свободно распространяемый генератор сеток Gmesh [4].
Рисунок 1 – Вид построенного остовного дерева на треугольной сетке
32
Из рисунка видно, что при использовании нерегулярной треугольной сетки в общем случае не удается сгенерировать строго трехдиагональную матрицу жесткости (в отличие от ситуации с регулярной прямоугольной сеткой, описанной в [3]). Однако построение остовного дерева указанным способом приводит к матрице жесткости, ненулевые элементы которой располагаются очень близко к главной диагонали, что позволяет эффективно применять прямые методы для решения конечноэлементной СЛАУ и, в итоге, значительно сократить время решения задачи конечноэлементного моделирования магнитного поля.
Работа проводилась при финансовой поддержке Министерства образования и науки Российской Федерации.
Литература
1.Соловейчик Ю.Г., Рояк М.Э., Персова М.Г. Метод конечных элементов для решения скалярных и векторных задач // Учебное пособие. Сер. «Учебники НГТУ». – Новосибирск: НГТУ, 2007. – 899 с.
2.Bossavit A. Computational Electromagnetism: Variational Formulations, Complementarity, Edge Elements. Academic Press, 1998, 352 p.
3.Домников П. А. Трехдиагонализация матрицы жесткости в векторном МКЭ с использованием метода деревьев-кодеревьев // Обработка информационных сигналов и математическое моделирование: Российская науч.-технич. конф., [23–24 мая 2013 г.]: материалы конф. – Новосибирск : СибГУТИ, 2013. – С. 47–
4.Geuzaine C. and J.-F. Remacle. Gmsh: a three-dimensional finite element mesh generator with built-in preand post-processing facilities. International Journal for Numerical Methods in Engineering 79(11), pp. 1309-1331, 2009.
РАЗРАБОТКА СРЕДСТВ ОПТИМАЛЬНОГО ВЛОЖЕНИЯ ГРАФА ПАРАЛЛЕЛЬНОЙ ПРОГРАММЫ В ГРАФ ВЫЧИСЛИТЕЛЬНОЙ СЕТИ
ЗабрудскихА.Е. НГТУ, Новосибирск e-mail: zabrae6@gmail.com
Научный руководитель – Родионов А.С., профессор СибГУТИ
В настоящее время широкое распространение получили такие технологии распределенных вычислений как облачные вычисления и GRID-сети, когда вычислительная среда является разнородной, то есть вычислительные узлы обладают различной вычислительной мощностью, а каналы связи между ними имеют разную пропускную способность.
Возникает научная проблема – отсутствие алгоритмов и методов оптимизации параллельных программ с учетом повышения их живучести в разнородной среде. Поэтому, цель моей работы – разработка алгоритмов исходной загрузки модулей параллельной программы и последующего их
33
перераспределения в ходе выполнения с целью балансировки нагрузки и с учётом потребной живучести программ. В связи с этим возникают следующие задачи:
1)разработка средств распределения потоков данных при решении больших и очень больших задач;
2)разработка алгоритмов оптимального размещения задачи с учетом повышения ее живучести;
3)разработка алгоритма оптимизации использования вычислительных ресурсов при решении задач конкретных классов.
Для решения поставленных задач предполагается построение гиперсетевой модели потоков данных, что является научной новизной. Кроме того, предполагается моделирование вычислительной среды и процессов в ней при вычислении больших задач с помощью мультиагентной системы AGNES.
Предполагаемые результаты исследований:
1)алгоритмы оптимизации использования ресурсов распределенной вычислительной среды с целью повышения живучести процессов решения задач конкретных классов;
2)имитационные модели функционирования сетей при решении конкретных задач;
3)экспериментальное программное обеспечение, реализующее разработанные алгоритмы.
ПРИМЕНЕНИЕ ФУНКЦИЙ СЛОЖНОСТИ ДЛЯ ОБРАБОТКИ СИГНАЛОВ В СИСТЕМАХ РАЗВЕДКИ ПОЛЕЗНЫХ ИСКОПАЕМЫХ
Морозов Ю.В. НГТУ, Новосибирск e-mail: sibfrost24@mail.ru
Анализ структуры земной коры с целью разведки полезных ископаемых осуществляется на основе изображений разрезов, полученных разными способами, например с помощью сейсморазведки и электроразведки. Разрез представляет собой зависимость некоей геофизической характеристики от глубины и положения по горизонтали. Разрез можно представить как совокупность функций глубины для разных положений по горизонтали. В этом случае выявленные неоднородности этих функций будут соответствовать границам слоев земной коры. Наиболее простым способом выявления границ на сейсмическом и геоэлектрическом разрезах является обнаружение максимумов производных соответствующих характеристик [1]. Данный способ дает приемлемые результаты для геоэлектрического разреза, поскольку зависимость удельного электрического сопротивления от глубины имеет вид близкий к ступенчатому. Следовательно, ее производная имеет ярко выраженные максимумы. В то же время, зависимость относительной амплитуды сейсмической волны от времени ее прихода на поверхность очень
34
похожа на случайный процесс с резкими перепадами уровня. Это означает, что для обнаружения неоднородностей сейсмического сигнала необходимо использовать более сложные методы, чем поиск максимумов производных.
В настоящей работе предложен вариант обработки геоэлектрических и сейсмических сигналов, полученных на основе соответствующих разрезов, с помощью функций сложности [2], которые позволяют изучать локальное поведение сложных кривых. Главное свойство функции сложности – наличие локальных экстремумов в точках изменения свойств экспериментальной кривой.
Для формирования функции сложности экспериментальная кривая разбивается на равные интервалы, для каждого из которых формируется вектор признаков на основе отсчетов, включенных в интервал. На основе векторов признаков различными способами вычисляются значения функции сложности. Затем для функции сложности обнаруживают локальные экстремумы, которые соответствуют изменениям свойств экспериментальной кривой.
Функцию сложности задают как функцию сходства между векторами признаков, функцию невязки между исходной и аппроксимирующей кривой, а также функцию авторегрессии. В качестве самих векторов абсолютные значения экспериментальной кривой, нормированные значения экспериментальной кривой, статистические моменты экспериментальной кривой по каждому интервалу.
Функция сходства для интервала j имеет вид:
|
|
1 |
f j 1 f |
j 1 , f |
j |
|
|
|
|
|
( j ) |
|
|
|
|||
|
|
|
|
(1) |
||||
где f j f1 j , |
, fl j |
2 |
|
|
|
, |
||
– вектор из l |
отсчетов |
экспериментальной |
кривой на |
|||||
интервале j. Функция сходства имеет смысл скалярного произведения вектора для текущего интервала на средний вектор между соседними интервалами.
Функция невязки в случае аппроксимации экспериментальной кривой с помощью ортогональных тригонометрических функций имеет форму
|
|
|
|
( j ) |
|
l |
|
|
|
n |
2 |
|
|
|
|
||
|
|
|
|
fsj |
cij sj |
|
|
|
|
||||||||
|
|
|
|
|
|
|
s 1 |
|
|
i 1 |
, |
|
|
|
(2) |
||
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
c ji fsj sj |
|
i |
|
i |
, |
, |
i |
– |
система ортонормированных |
векторов с |
||||||
|
|
1 |
l |
||||||||||||||
s 1 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
координатами, |
соответствующих |
|
|
значениям |
некоторых |
базисных |
|||||||||||
тригонометрических функций. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Функция авторегрессии определяется выражением |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
l |
1 |
|
n |
|
2 |
|
|
|
|
|
|
|
( j ) min |
|
|
fsj |
c0 ci fs 1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
C |
s 1 b |
|
i 1 |
|
|
, |
(3) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где минимум берется по векторам C c0 , |
,cn . |
|
|
||||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
35 |
|
|
|
|
|
||

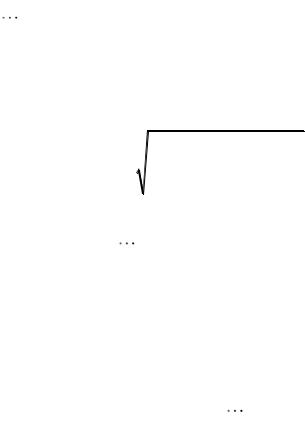
Как показало компьютерное моделирование (рисунки 1-3), у функции сходства затруднительно выделить локальные экстремумы, соответствующие разным состояниям исследуемой зависимости сейсмической волны от времени прихода.
Рисунок 1 – Зависимость относительной амплитуды сейсмической волны от времени прихода на поверхность для фиксированного положения
по горизонтали
Рисунок 2 – Функция сходства
Рисунок 3 – Функция авторегресии
Наиболее ярко выраженные экстремумы наблюдаются у функции авторегресии, поскольку ошибка приближения сильно зависти от характера
36
изменения аппроксимируемой функции. Минимум функции авторегрессии или максимум функции сходства позволяют оценить время прихода, соответствующее границе между слоями земной коры. Наличие этой границы подтверждается наличием максимума производной зависимости электрического сопротивления от глубины на геоэлектрическом разрезе.
Литература
1.Морозов Ю. В. Совместное моделирование сигналов при интерпретации геоэлектрических и сейсмических разрезов / Ю. В. Морозов // Решетневские чтения : материалы 27 междунар. науч. конф., посвящ. памяти генерала конструктора ракет.-космич. систем акад. М. Ф. Решетнева : в 2 ч., Красноярск,
12–14 нояб. 2013 г. – Красноярск, 2013. – Ч. 2. – С. 64–66.
2.Браверман Э.М. Структурные методы обработки эмпирических данных / Э.М. Браверман, И.Б. Мучник // М.: Наука. Главная редакция физиоматематической литературы, 1983. – 464 с.
ИССЛЕДОВАНИЕ АЛГОРИТМА РАНГОВОЙ СЕГМЕНТАЦИИ ТЕПЛОВИЗИОННОГО ИЗОБРАЖЕНИЯ
Подрезов Р.В., Райфельд М.А. НГТУ Новосибирск
e-mail: podrezov-r.v@mail.ru
Для ряда прикладных задач представляет интерес проблема бинарной яркостной сегментации полутоновых изображений. Изображения, адекватно описываемые бинарной моделью, являются достаточно распространенными (это касается и моделей тепловизионных изображений в задачах обнаружения объектов с внутренним тепловым источником). Предполагается, что такие изображения включают в себя области двух типов – статистически более яркого объекта и менее яркого фона.
Достаточно часто задачу сегментации приходится решать в условиях априорной неопределенности относительно вида функции распределения (ФР) яркости классов. В этом случае строятся гипотезы самого общего вида, как, например, гипотеза сдвига:
F1 (x) F0 (x ) , |
(1) |
либо гипотеза о том, что ФР фона больше ФР объекта для любых значений яркости:
F0 (x) F1 (x), x . |
(2) |
Выражения (1), (2) формализуют приведенное выше утверждение о том, что отсчеты объекта статистически более яркие, чем отсчеты фона.
Под фоном мы будем понимать все естественные образования: облака, атмосферу, почву, лес, снежный и ледяной покров и т.п. Фон есть окружающая среда, не имеющая внутреннего теплового источника. Объектом мы будем
37
называть транспортные средства, и их температура статистически выше фона из-за внутреннего нагрева.
Существующие методы
Существует значительное разнообразие алгоритмов сегментации изображений, применяющихся при указанных выше условиях. Большинство непараметрических алгоритмов сегментации изображений базируется на использовании оценок плотности вероятности (ПВ) наблюдений (гистограмм). Например, широко известен алгоритм квантования мод [1], осуществляющий пороговую классификацию отсчетов изображения. Порогам классификации в этом алгоритме соответствуют локальные минимумы гистограммы, расположенные между модами (которые ассоциируются с центрами распределений яркости соответствующих классов). Основной проблемой использования этого алгоритма является сложность локализации указанных минимумов. Вообще говоря, наличие минимумов можно гарантировать лишь при достаточно больших расстояниях между яркостными классами и для плотностей с ярко выраженными модами.
Описание алгоритма ранговой сегментации
Предлагается использовать процедуру пороговой сегментации, подобную по форме той, что используется для алгоритма квантования мод, применительно к рангам отсчетов изображения совместно с проверкой гипотезы об однородности изображения (т.е. принадлежности рабочей выборки и изображения в целом одному и тому же закону распределения). Обычно заранее неизвестно, имеются ли на изображении объекты, подлежащие обнаружению, или оно состоит только из элементов фона (является однородным). Поэтому представляет интерес получить решение этой задачи до выполнения собственно сегментации. С помощью рангового метода это можно сделать достаточно просто с устойчивыми показателями качества.
Пусть H1 – гипотеза о неоднородности изображения (альтернатива), H0 –
гипотеза, утверждающая о том, что изображение однородно. Решение принимается с использованием правила:
H |
, C |
|
|
|
( ) |
1 |
, |
(3) |
|
0 , C |
||||
H |
|
|
где C – порог принятия решения, который зависит от выбранного критерия.
В нашем случае это критерий Неймана-Пирсона, в соответствии с
которым: |
|
|
|
|
|
|
|
|
|
|
P(R | H |
0 ) |
, |
(4) |
|
|
|
|
|
|
( R ) C |
|
|
|
где – заданная вероятность ложной тревоги. |
|
|
||
Предположим, что изображение неоднородно, и на нем имеется l |
точек |
|||
фона и n l точек объекта (n – общее число точек на изображении). Согласно выражению (2) распределения классов не перекрываются, и их безошибочное разделение возможно с использованием правила:
38
|
0, |
R lˆ |
, |
(5) |
|
di (Ri ) |
i |
||
|
|
|
|
|
|
1, R lˆ |
|
|
|
|
|
i |
|
|
где lˆ |
– оценка кол-ва элементов фона на изображении, |
|
||
Ri |
– ранг i -той точки изображения. |
|
|
|
Сформируем рабочую выборку рангов{R1 , R2 , , Rm } |
объемом m из |
|||
отсчетов некоторого произвольного участка изображения. В рабочей выборке
будем оценивать количество элементов фона ˆ , построив вариационный ряд k
{R(1) , R( 2) , , R(m) }.
МП оценкой |
ˆ |
при гипотезе |
k |
минимум выражения [2]:
ˆ
k k1 ,
H1 , считается значение k1 , обеспечивающее
min C |
k1 |
|
|
C |
m k1 |
|
|
, |
(6) |
( k ) |
1 |
( k ) |
1 |
||||||
k |
R |
1 |
|
n R |
1 |
|
|
||
1 |
|
|
|
|
|
|
|
|
|
где C x |
y! |
биномиальный коэффициент. |
|
|
|
||
|
|
||
y |
x!( y x)! |
|
|
|
|
||
МП оценка lˆ при этом вычисляется согласно выражению [2]
lˆ R( k ) 1. |
(7) |
Принятие решения об однородности изображения выполняется в соответствии с критерием отношения максимального правдоподобия.
Отношение правдоподобия для упорядоченного рангового вектора наблюдений
рабочей выборки R можно представить в виде:
|
|
|
|
, k, l) |
|
|
|
|
|
|
|
max P(R / H1 |
|
|
m |
|
|
|
|||||
(R) |
|
|
|
|
|
ˆ |
|
ˆ |
. |
(8) |
|
|
k ,l |
|
|
|
|
|
Сn |
|
|
|
|
|
|
P(R / H |
0 |
) |
|
C k |
ˆ |
C m k |
ˆ |
|
|
|
|
|
|
|
R( k ) 1 |
n R( k ) 1 |
|
||||
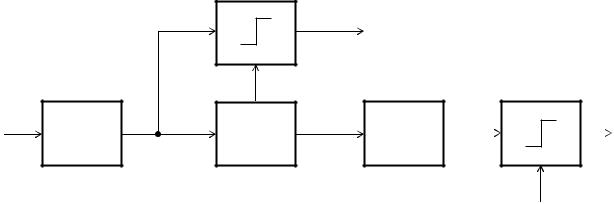
На рисунке 1 представлена схема рангового алгоритма.
Рисунок 1 – Схема рангового алгоритма
Где изображены блоки ранжирования, оценки кол-ва элементов фона, вычисления отношения правдоподобия, порога гипотезы однородности, а так же пороговые устройства.
39

Пример сегментации
Цифровое тепловизионное изображение размером 320x240 приведено на (рисунок 2).
Рисунок 2 – Исходное изображение
В ранжированном изображении яркость заменена рангами от 0 до 76799. В этом случае n 76800 . Ранжированное изображение, приведенное к диапазону яркостей монитора, выглядит следующим образом (рисунок 3).
Рисунок 3 – Ранжированное изображение
Рабочая выборка формируется из части отсчётов исходного изображения,
для чего оно |
разбивается |
на блоки 48x64, (m 3072) . Для каждого блока |
||||
строится вариационный ряд из рангов отсчётов. Далее в каждом |
i -м блоке |
|||||
вычисляются МП оценки ki |
и li в соответствии с алгоритмом (6), (7). Во |
|||||
избежание |
переполнения |
сравнение |
при |
вычислении |
максимума |
|
осуществляется для логарифма статистики. |
|
|
|
|||
Результирующая оценка lˆ выбирается в соответствии с выражением: |
||||||
|
|
lˆ l |
, min C ki C m ki . |
|
(9) |
|
|
|
i |
i |
li n li |
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
