Симонов Томографические измерителные информационные системы 2011

Поскольку выбор A не согласован с δ, то при А→ ∞, как видно из (2.117), величина A , вообще говоря, не будет стремиться к

нулю.

Таким образом, рассмотренные примеры показывают, что нельзя в качестве приближенного решения уравнения (2.110) брать его

точное решение с приближенной правой частью Р(l, θ) , т. е. нельзя братьэлемент μ(x, y) =T −1 P (l, θ) , таккак:

1) такого решения может не существовать на множестве L2

пространства R2 ;

2) если такое решение существует, то оно может не обладать свойством устойчивости к малым изменениям правой части Р(l, θ)

уравнения (2.110).

Условие устойчивости решения задачи (2.110) связано с общим физическим принципом детерминизма, и его невыполнение означает невозможность придать физический смысл найденному решению.

Другими словами, это означает, что при различных погрешностях в получении проекционных данных Р(l, θ) некоторое решение

уравнения (2.116), т. е. реконструкция изображения физической величины μ , все-таки происходит, и мы получим изображение μ ,

пусть и зашумленное, но обладающее вполне определенным физическим приближенным смыслом. Это подтверждается при практических исследованиях.

Возникает вопрос: что следует понимать под приближенным решением уравнения (2.110).

Ответ на этот вопрос, как показали авторы [11], зависит от структуры множества, в котором ищется приближенное решение и

которому принадлежит точное решение (т. е. решение μ0 (x, y) уравнения (2.110), соответствующее некоторой функции Р0 (l, θ) ).

Ими был развит подход для общего случая, когда приближенное решение не принадлежит множеству, где имеется точное решение. Идея этого подхода заключается в обосновании применимости принципа регуляризации к нахождению приближенных решений уравнения (2.110).

161

В [11] доказано, что применение принципа регуляризации к операторному уравнению I рода с линейным непрерывным оператором позволяет получить устойчивое решение.

где Х, Y – метрическое пространство; А – непрерывный оператор, такой, что обратный ему оператор А–1 (если он существует) не является непрерывным в пространстве Y.

Пусть Х0 – множество возможных решений уравнения (2.118) и некоторому элементу y0 Y соответствует решение уравнения

(2.118) x0 X0 , Ax0 = y0 , но вместо точных исходных данных у0 и А имеются приближенные данные yδ и А, а δ > 0 – оценка сверху погрешности задания у0. Требуется по yδ , А, δ найти приближение xδ к элементу x0 , которое было бы устойчиво к малым изме-

нениям у.

В п. 2.3.4 был приведен пример, показывающий, что в качестве

ям правой части. Поскольку числовой параметр δ > 0 характеризует погрешность правой части уравнения (2.118), то естественно определить приближенное решение xδ этого уравнения с помощью

оператора, зависящего от этого параметра так, чтобы при δ → 0 была сходимость

ρx0 (x0 , xδ ) → 0 .

Оператор Rα ( y) , зависящий от параметра α > 0 и действую-

щий из Y в X , называется регуляризирующим оператором для уравнения (2.118), если он обладает следующими свойствами:

162

1) существуют числа δl > 0 , α0 > 0 , такие, что оператор Rα ( y) определен для любых α (0,α0 ) и y Y , таких, что ρy ( y0 , y) ≤ δ0 ;

ρX0 , (x0 , xα ) ≤ ε , где xα = Rα ( y,α(δ, y)) .

Имея в виду свойства регуляризирующих операторов, естественно в качестве приближенного решения уравнения (2.118) с приближенно известной правой частью yδ брать значение регуляризи-

рующего оператора RαYδ c α = α(δ) . Получаемые приближенные

решения называют регуляризированными решениями.

Очевидно, что любой регуляризирующий оператор с указанным способом выбора параметра регуляризации α > 0, согласованного с δ, определяет устойчивый к малым изменениям правой части уравнения (2.118) метод приближенного решения этого уравнения.

Таким образом, задача нахождения приближенных решений уравнения (2.118), устойчивых к малым изменениям правой части, сводится к построению регуляризирующих операторов и к определению параметра регуляризации α > 0 по имеющейся информации о задаче реконструкции изображения. Указанный принцип построения приближенных решений уравнения (2.118) называется принципом регуляризации.

Построение регуляризирующих операторов рассмотрено в работах [3, 11]. Можно выделить несколько подходов в построении регуляризирующих операторов.

Вариационный метод. Пусть Ω[x] – стабилизирующий функционал, определенный на множестве Х Х . Рассмотрим элемент х Х ∩ Хδ и вариационную задачу

163

При использовании вариационного метода нахождения регуляризирующего решения уравнения (2.118) задача сводится к нахождению элемента Хδ, минимизирующего функционал Ω[x] на множестве Х ∩ Хδ . В качестве функционала Ω[x] выбирают такой,

который в составе сглаживающего функционала Mα [ x, yδ] имеет вид

При построении регуляризирующих операторов путем минимизации сглаживающего функционала Mα [ x, yδ] параметр регуляри-

зации α как функция δ определяется неоднозначно [11]. Это открывает возможность использования дополнительной априорной информации для нахождения приближенного решения, устойчивого к изменениям исходных данных. В методе локальной регуляризации (рассматривается ниже) рассмотрим априорный способ выбора α . А в этом методе выбор α определяется по невязке. Пусть имеется

ным. Условия разрешимости этого уравнения должны обладать следующими свойствами [11]: пусть

m(α) = Mα [ xα, yδ], ϕ(α) = ρ2y ( A xα, yδ ) , ϕ(α) = Ω[ xα ],

1)функции m(α) и ϕ(α) являются неубывающими, а функция

ψ(α) монотонно не возрастающей;

ϕ(α) и ψ(α) строго монотонны;

3)функции m(α) , ϕ(α) и ψ(α) полупрерывны справа и слева для любого α > 0 .

164

На практике определение α по невязке осуществляется следующим образом. Берется конечная монотонно убывающая последова-

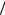α = (1γ) .

Приближенные устойчивые решения уравнения (2.118) можно построить с помощью итерационных методов. Основная задача при этом состоит в построении аппроксимирующей последовательности и выборе правила согласования номера последовательностей итерации с уровнем погрешности исходных данных.

Построение регуляризирующих операторов в случае, когда оператор A уравнения (2.118) является интегральным оператором типа свертки:

−∞

где y (t ) L2 (−∞,∞) , K (t ) L1 (−∞,∞) , x(τ) L2 (−∞,∞) .

Обозначим через y (ν) , K (ν) , x(ν) соответственно фурьеобразы функций y (t ) , K (t ) , x(τ) . Пусть ψ( y (ν),ν) = y (ν)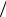K (ν) . Рассмотрим операторы вида R f ( y,α) = F −1{ψ( y (ν),ν) − f (ν,α)} , где F −1 – преобразование обратное преобразованию F ; f (ν,α) – некоторая заданная функция.

Для фурье-преобразования оператор Rf ( y,α) имеет вид

165

регуляризирующим оператором для уравнения (2.122), то функция

функция, такая, что:

1)она кусочно непрерывна на любом конечном отрезке;

2)M (ν) ≥ 0 , M (0) ≥ 0 , при ν ≠ 0 ;

3)M (ν) ≥ C > 0 для достаточно больших ν ;

166

При этих условиях регуляризованное решение определяется по формуле xα = Rf ( yδ,α) , где f (ν,α) берется в виде (2.124).

Функцию f (ν,α) в компьютерной томографии называют

функцией «окна», так как она с ее свойствами а)–з) обладает не только регуляризирующими свойствами в зависимости от значения параметра регуляризации α, но и фильтрующими свойствами, т. е. значения ее зависят также от области работы оператора (2.122).

n

Полагая М (ν) = ∑ gn ν2n , где gn > 0 – заданные не отрица- n =0

тельные постоянные, можно получить стабилизаторы n -го порядка. Целесообразность рассмотрения различных типов регуляризирующих операторов состоит в том, чтобы для конкретной задачи выбрать наилучший в некотором смысле оператор. Далее в гл. 3 рассматриваются некоторые типы регуляризирующих «окон» применительно для параллельной и веерной геометрии рентгеновского пучка, а в гл. 4 анализируются вопросы точности входных данных yδ и точности реконструированного изображения в зависимости от

параметра регуляризации α и других параметров реконструкции.

Метод локальной регуляризации. Указанные выше подходы используют главным образом либо информацию количественного характера об уровне погрешности задания оператора и исходных проекционных данных, либо информацию качественного характера, когда задан класс корректности решаемой задачи.

Во многих задачах томографии имеется дополнительная информация об искомой функции, искомом точном решении и других исходных данных, полученная, например, путем моделирования томографического процесса. Использование этой информации при построении регуляризирующих алгоритмов позволяет повысить эффективность применения регуляризации.

Характерным примером этого является задача нахождения формы радиоимпульса х(t), испущенного источником излучения, по результатам его регистрации y(t) на больших расстояниях, если известна импульсная функция трассы K(t). Эта задача сводится к решению интегрального уравнения I рода типа свертки (2.122). При

167

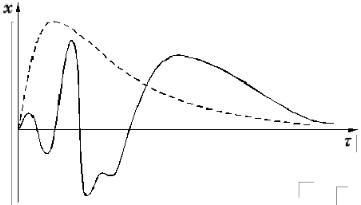
этом характерной дополнительной информацией о данной задаче является информация о форме импульса x(τ) (рис. 2.23).

Рис. 2.23. Графики типичных радиоимпульсов

Интуитивно можно предположить, что каждому интервалу резкого и плавного изменения функции х(τ) при решении уравнения (2.122) должен соответствовать свой параметр регуляризации α.

Данный подход может использоваться в томографии через определение функции отклика у (функции изображения) на δ- функцию х в виде тонкого стержня, реконструкцию которого необходимо провести. Здесь необходимо иметь информацию о точной форме сигнала х (точная форма томографического стержня), а также информацию об импульсной функции томографа в виде заданной апертуры детектора.

Снова рассмотрим уравнение (2.122). Пусть элементу g0 (t ) L2 соответствует единственный элемент x0 (τ) L2 , но вместо эле-

мента y0 (t ) задано его приближение yδ (t ) , такое, что yδ (t ) = y0 (t) + N (t ) ,

где N (t ) – случайная функция с математическим ожиданием

Случайная функция N (t ) априорно определена. Тогда можно найти регуляризирующий оператор вида [11]

где р – целые числа. Число α выбирается либо по невязке, либо другим способом [11].

2.3.6. Построение регуляризирующих алгоритмов

Рассмотрим задачу нахождения приближенных решений основного уравнения компьютерной томографии (2.110).

где L(l, θ) – прямая в R2, задаваемая уравнением x cos θ + y sin θ = l

(l (−∞,∞),θ (0, π)) .

x cos θ + y sin θ = l , то уравнение прямой L(l, θ + π) имеет вид x cos(θ+ π) + y sin (θ+ π) = −xcos θ − y sin θ,

поэтому

169

2.Пусть P(ν,θ) – фурье-образфункции P(l,θ) по переменной l , а

μ(ν1,ν2 ) – фурье-образ функции μ(x, y) . Тогда справедливо равен-

где ν = (ν12 + ν22 )1 2 . Тогда, применяя к соотношению

∞ ∞

Р(l,θ) = ∫ ∫ μ(x, y)δ(x cos θ + y sin θ −l )dx dy

−∞−∞

оператор преобразования Фурье по переменным х, у и учитывая связь этого преобразования с преобразованием Радона (2.87), получим (2.127). Преобразуем правую часть уравнения (2.125)

π

Обозначая ∫Р(l, θ)dθ = S (x, y) , получим из (2.128) следующий

0

оператор Kμ [12]

где Kμ ≡ K (x, y)*μ(x, y) , * – свертка; K (x, y) = (x2 + y2 )−12 ; ξ , η

– координаты локальной области (точки) в круге r = х2 + у2 . При фиксированном α > 0 существует единственное решение

μα (x, y) уравнения (2.129), которое можно записать в явном виде

[11]:

170