
Никитенко Нестационарные процессы переноса и 2011
.pdf
трон-фононное взаимодействие. Роль фононов в прыжковом транспорте, пожалуй, противоположна той, которую они играют в транспорте по делокализованным (протяжённым) состояниям – там рассеяние на фононах уменьшает проводимость, а прыжковая проводимость в неупорядоченной среде возможна только благодаря взаимодействию с фононами.
В том случае, когда разность энергий состояний λ и λ' не превышает максимальной энергии фонона, Eλ − Eλ' < ωD ( ωD – деба-
евская частота), основную роль играют переходы с испусканием или поглощением одного фонона. При слабом перекрытии волновых функций состояний λ и λ' , задача решается в 1-м порядке квантовомеханической теории возмущений [1:1, 4]:
νλλ' = |
2π |
|
Hλλ' |
|
2 N ph , |
(1.54) |
|
|
|
||||||
|
где Hλλ' – матричный элемент гамильтониана электрон-фононного взаимодействия, взятый с волновыми функциями начального и конечного состояний, Ψλ и Ψλ' . Рассмотрим взаимодействие локализованного электрона и акустического фонона с волновым числом q и частотой ω = qs = Eλ − Eλ' 
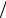 , где s – скорость звука. В уравнении (1.54) N ph – энергетическая плотность состояний фононов с
, где s – скорость звука. В уравнении (1.54) N ph – энергетическая плотность состояний фононов с
энергией E = ω (и импульсом p = |
q ) [35]: |
|
|
|
|||||||
N |
ph |
= |
Ω |
4πp2 |
dp |
= |
Ωq2 |
|
, |
(1.55) |
|
(2π )3 |
dE |
2π2 |
s |
||||||||
|
|
|
|
|
|
||||||
где Ω – объём образца. Малые деформации (периодические в пространстве и времени) создают линейные (по деформации) поправки к энергии электрона, которые характеризуются величиной с размерностью энергии – константой деформационного потенциа-
ла Edef . Эта константа служит мерой изменения энергии электрона при малых относительных деформациях: δE=Edef divu= Edef δΩ Ω, где u - вектор деформации, δΩ
Ω, где u - вектор деформации, δΩ Ω – относительное изменение объёма вследствие деформации в данном месте [1:2], u = er x exp(iqr) . Таким образом, электрон-фононное взаимодействие записывается в виде [1:2, 4] H = iEdef qxexp(iqr), где x – амплитуда деформации, а
Ω – относительное изменение объёма вследствие деформации в данном месте [1:2], u = er x exp(iqr) . Таким образом, электрон-фононное взаимодействие записывается в виде [1:2, 4] H = iEdef qxexp(iqr), где x – амплитуда деформации, а
51

квадрат модуля матричного элемента, взятого с осцилляторными волновыми функциями, xn,n+1 2 = Cq {nq , nq +1}, где первое и второе
выражение в скобках отвечают случаю поглощения и испускания фонона (т. е. переходу вверх или вниз по энергии),
Cq = |
(2mω) = |
|
(2Ωsqd ) , m = Ωd , |
d – плотность вещества [1:1], |
||||||||||||||||||
q |
|
|
( |
qs kT |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
= exp |
|
|
−1 −1 . Таким образом, из (1.54), (1.55) следует |
||||||||||||||||||
|
|
|
ν |
λλ' |
= |
Edef |
2q3 |
n |
, n |
+1 |
|
∫ |
Ψ |
* exp(iqr)Ψ |
λ' |
dΩ |
|
2 , |
(1.56) |
|||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
{ q |
q |
} |
|
|
λ |
|
|
|
|
||||
|
|
|
|
|
|
2π |
|
s |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где q = ω s = Eλ − Eλ'
s = Eλ − Eλ' 
 s . Множитель в фигурных скобках создаёт основную зависимость от энергии ( nq и nq +1 – для переходов
s . Множитель в фигурных скобках создаёт основную зависимость от энергии ( nq и nq +1 – для переходов
вверх и вниз, соответственно). Поскольку волновые функции локализованных состояний убывают экспоненциально с удалением от
центра локализации, Ψ exp(−γr ) , где γ – обратный радиус локализации, а множитель exp(iqr) в интеграле (1.56) быстро осциллирует, этот интеграл «набирается» в области qr <<1, где одна из
подъинтегральных волновых функций экспоненциально мала в случае сильной локализации ( γr >>1 ). Поэтому основная зависи-
мость частоты перехода от r является экспоненциально убывающей функцией, νλλ' exp(−2γr ). Итого, основная зависимость час-
тоты перехода от разности энергий и расстояния между ЛС, следующая из (1.56), выглядит следующим образом [1:5]:
νλλ' = νλλ0 |
|
E |
− E |
|
|
|
E |
λ |
− E |
λ' |
|
|
|
|
|
|
|
|
|||||||||||||
' exp |
λ |
λ' |
− 2γr |
sh |
|
|
|
|
|
|
. |
(1.57) |
|||
2kT |
|
|
|
2kT |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Вычисление интеграла в (1.50) было выполнено Миллером и Абрахамсом для случая переходов между водородоподобными примесными центрами в легированных полупроводниках [1:3–5,
37]. Показано, что фактор νλλ0 |
' |
в (1.51) зависит от разности энергий |
||||||||||||||||||||||
и расстояния лишь по степенному закону, |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
E |
− E |
|
|
|
|
e |
2 |
γ |
2 |
r |
2 |
|
|
E |
− |
E |
2 |
−4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
νλλ0 |
' = |
|
|
λ |
|
λ |
' |
|
|
Edef |
|
|
|
1 |
+ |
|
|
. |
(1.58) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
λ' |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
πs |
5 4 |
d |
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
6πε0 |
|
|
sγ |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52

Очевидно, уравнения (1.57), (1.58) удовлетворяют условию (1.51). Легко заметить, что главные асимптотические зависимости час-
тот переходов от разности энергий |
E = Eλ' |
− Eλ при |
|
|
E |
|
kT >>1 |
|
|
||||||
имеют следующий вид: νλλ' exp(− |
E kT ), |
E > 0 , и νλλ' ≈ const, |
|||||
E < 0 (если пренебречь степенными зависимостями, |
например |
||||||
(1.58)). Такие же асимптотические зависимости получены и для случая многофононных переходов (именно такие переходы характерны для неупорядоченных органических материалов, когда E может достигать многих десятых электронвольта, так что E >> ωD ). По-видимому, наиболее простым объяснением может
служить следующее [1:4]. Энергия локализованного носителя подвержена случайным колебаниям с частотой ω вследствие взаимодействия с фононами (иначе – вследствие колебаний размеров и глубины потенциальных ям, в которых носители локализованы, см. штриховые линии на рис. 1.9). Для сильно локализованных состояний в органических материалах классический надбарьерный переход (через точку М) практически невозможен. Туннельный переход (стрелка 2 на рис. 1.9) возможен, когда энергии промежуточных состояний находятся в пределах узкой полосы порядка интеграла перекрытия I . Вероятность реализации такого состояния в единицу времени (стрелки 1 и 3 на рис. 1.9) для переходов вверх по энер-
гии пропорциональна ωexp(− E kT ) . Время, в течение которого
kT ) . Время, в течение которого
туннелирование возможно, пропорционально ширине полосы I , а вероятность туннелирования в единицу времени составляетI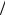 (т.е. вероятность туннелирования пропорциональна I 2 exp(−2γr) ). Именно асимптотические зависимости νλλ' , как
(т.е. вероятность туннелирования пропорциональна I 2 exp(−2γr) ). Именно асимптотические зависимости νλλ' , как
правило, определяют характеристики транспорта в неупорядоченных системах. Поэтому широкое распространение получила упрощённая модель, часто называемая моделью Миллера – Абрахамса, в
которой частота прыжков носителя на расcтояние r = rλλ' с ЛС
энергии E = Eλ на ЛС энергии E ' = Eλ' , определяется экспоненциальной зависимостью (которая также удовлетворяет условию
(1.51)), |
( |
|
) |
0 |
|
|
( |
) |
|
|
ν |
r, E, E ' |
−u |
(1.59а) |
|||||||
|
|
= ω |
exp |
|
r, E, E ' , |
53

где
u (r, E, E ')= 2γr +(E '− E)η(E '− E) kT (1.51)) – (1.59б)
kT (1.51)) – (1.59б)
прыжковый параметр, η(x) – единичная функция. Здесь обратный радиус локализации волновых функций γ и частотный фактор ω0 представляют собой феноменологические константы.
|
M |
|
r |
|
λ ' |
|
2 |
|
3 |
λ 1 |
E |
Рис. 1.9. Схема перехода между состояниями λ и λ' .
Кроме частоты, большое значение при вычислении проводимости неупорядоченных материалов играет темп переходов – вероятность переходов в единицу времени между ЛС, которая учитывает вероятность заполнения как начального, так и конечного состоя-
ний: Γλλ' = νλλ' fλ (1− fλ' ). Надо заметить, что частоту νλλ' также часто называют темпом переходов (англ. rate) [1:37]. Действительно, это темп переходов с ЛС λ на ЛС λ' при условиях fλ =1 и
fλ' = 0 , которые естественно выполняются в задаче одного носите-
ля (например, если выполняется численное моделирование движения одного носителя, и потом усредняются результаты многих испытаний [1:37, 14]). Величину ν , определяемую уравнениями (1.59), часто применяют в случае низкой концентрации носителей, когда числа заполнения очень малы (но могут зависеть от коорди-
нат и времени, в отличие от νλλ' ), так что применимы кинетиче-
ские уравнения типа (1.49). Именно такие задачи в основном рассматриваются в этой книге. Если же заселённость состояний близка
54
к равновесному распределению Ферми (1.50), удобно выражать проводимость через равновесный темп переходов
Γλλ' = νλλ' fF (Eλ ) 1− fF (Eλ' ) . Можно показать, что в этом случае
(при слабом и постоянном электрическом поле) образец можно рассматривать как сетку сопротивлений. Все ЛС – узлы этой сетки, причём в принципе любая пара ЛС связана между собой «проводом», обратное сопротивление которого при движении носителя от
ЛС λ на ЛС λ' , Zλλ−1' , пропорционально равновесному темпу переходов: Zλλ−1' = (e2 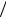 kT )Γλλ' [1:5]. Нетрудно убедиться, что, если ха-
kT )Γλλ' [1:5]. Нетрудно убедиться, что, если ха-
рактерные разности энергий велики по сравнению с kT , основная (экспоненциальная) зависимость равновесных темпов переходов от расстояний и энергий имеет вид, напоминающий (1.59):
Γλλ' = Γ(rλλ' , Eλ , Eλ' )≡ Γ(r, E, E ')= Γ0 exp −ς(r, E, E ') , |
(1.60а) |
||||||||||||
ς(r, E, E ')= 2γr + |
|
E − EF |
|
+ |
|
E '− EF |
|
+ |
|
E − E ' |
|
. |
(1.60б) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2kT |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Большой разброс величин Γλλ' (следовательно, и сопротивлений Zλλ' ) приводит к тому, что большая часть связей практически разо-
рвана, и лишь малая часть сетки реально создаёт проводимость, см.
разд. 1.6.
1.5.3. Проводимость с переменной длиной прыжка
Положение уровня Ферми в области состояний, квазинепрерывно распределённых по энергии, не даёт проводимости металлического типа, если эти состояния локализованы. При достаточно низких температурах в неупорядоченных материалах часто наблюдается «дробно–экспоненциальная» зависимость проводимости от
температуры, G exp(−const T1
T1 4 ) [1:4, 1:5].
4 ) [1:4, 1:5].
Рассмотрим температурную зависимость стационарной проводимости, которая контролируется термоактивированными прыжками по состояниям вблизи уровня Ферми, причём как изменения энергии носителя в ходе прыжка, так и длины прыжков разбросаны случайно и не зависят друг от друга. Проводимость может быть вычислена перемножением следующих величин: концентрации
55
электронов в области шириной kT вблизи уровня Ферми (которую можно оценить как g (EF )kT ), заряда носителя e , типичной длины прыжка a , разности частот термоактивированных прыжков вдоль и против поля, νexp(±eF0a kT ), и делением полученной плотности тока на напряжённость приложенного поля F0 . При достаточно слабом поле, eF0a
kT ), и делением полученной плотности тока на напряжённость приложенного поля F0 . При достаточно слабом поле, eF0a kT <1 , получается
kT <1 , получается
G e2a2 g (EF )ν . |
(1.61) |
Согласно (1.59), типичную частоту термоактивированных прыжков ν можно записать в следующем виде:
ν =ν |
0 |
|
( |
2γa + |
E kT |
) |
(1.62) |
|
exp − |
|
. |
Температуру считаем достаточно малой для того, чтобы можно было пренебречь изменением энергетического распределения
прыжковых центров g (E) |
вблизи уровня Ферми, если энергия из- |
меняется на величину E : |
g (E)≈ g (EF ). |
При сильной локализации, γa >>1 , вероятность прыжка резко убывает с ростом расстояния a. Поэтому типичная длина прыжка a связана с энергией активации E условием, что внутри сферы радиуса a и в области энергий от EF до EF + EF есть (в среднем) только одно соседнее состояние, на которое и происходит прыжок:
(4π 3)a3 g (EF ) |
E =1. |
(1.63) |
Уравнение (1.63) даёт связь между a и |
E , поэтому прыжковый |
|
параметр, т. е. выражение в круглых скобках в уравнение (1.62), можно рассматривать как функцию a. Максимальная вероятность прыжка, очевидно, достигается при минимальном значении прыж-
кового параметра. Значение a = (9 8π)1
8π)1 4 γg (EF )kT −1
4 γg (EF )kT −1 4 , при кото-
4 , при кото-
ром прыжковый параметр минимален, можно считать типичной прыжковой длиной. Подстановка этого значения в уравнения
(1.61) – (1.63) даёт закон Мотта:
|
|
G = G0 exp(−B T1 4 ), |
(1.64) |
||||
2 |
2 |
|
γ |
3 |
1 4 |
, |
|
гдеG0 e |
a |
g (EF )ν0 , B = B0 |
|
kg (EF ) |
|
||
56
B0 = (8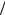 3)(9
3)(9 8π)1
8π)1 4 ≈ 2,06 . Мотт, выполнив усреднение по длинам
4 ≈ 2,06 . Мотт, выполнив усреднение по длинам
прыжка, получил значение B0 = 2(3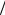 2π)1
2π)1 4 ≈1,66 [1:4]. Основную
4 ≈1,66 [1:4]. Основную
температурную зависимость даёт экспоненциальный множитель в уравнении (1.64). Надо заметить, что приведённые выше рассуждения носят качественный характер: в правой части (1.63) должна быть величина >1, а область в r – E пространстве выглядит сложнее, чем предполагалось при выводе (1.63). Более строгим подходом является теория протекания, при этом, однако, получено
B0 = 2.05 (см. разд. 1.6).
Выражение (1.64) относится к случаю слабого поля. В обратном предельном случае, eF0a kT >>1 , электрон совершает прыжки в
kT >>1 , электрон совершает прыжки в
основном вдоль поля без термической активации. При этом многими авторами (см. обзоры [1:3, 4, 38, 39]) было получено темпера-
турно-независимое выражение, G exp(−B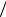 F01
F01 4 ), в котором на-
4 ), в котором на-
пряжённость поля «играет ту же роль», что и температура в уравнении (1.64). Данная закономерность послужила основанием кон-
цепции эффективной температуры, введённой Шкловским и Эф-
росом [1:3, 40]. Действительно, пусть температура равна нулю. Прыжок вдоль поля без термической активации со значительной вероятностью приводит к повышению энергии носителя на величину eF0a , как это имело бы место в случае термической актива-
ции при температуре Teff ≈ eF0a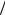 k . Применение численного моде-
k . Применение численного моде-
лирования для случая гауссовского распределения ЛС по энергии [1:38] и методов теории протекания [1:39] даёт следующую зависимость эффективной температуры от напряжённости поля и температуры:
Teff (T , F0 )= T s +(ξeF0a k )s 1
k )s 1 s ,
s ,
где s = 2 [1:38] и 1,5 [1:39]. Однако числа ξ получаются несколько
различными для случаев дисперсионного и квазиравновесного транспорта ( ξ = 0,6 и ξ = 0,9 соответственно) [1:38]. Это говорит о
том, что концепция эффективной температуры не даёт универсального описания всех режимов транспорта, хотя может быть хорошим первым приближением.
57

1.5.4. Дрейф, диффузия и соотношение Эйнштейна
Вданном разделе на простом примере показано, каким образом
ив каких приближениях из уравнения баланса типа (1.36) получается дрейфово-диффузионное уравнение типа (1.8) для прыжкового транспорта и соотношение Эйнштейна (1.13) между подвижностью
икоэффициентом диффузии. Рассмотрим кубическую решётку ЛС
содинаковой энергией (изоэнергетические ЛС), a – постоянная
решётки. Для простоты будем считать, что состояния локализованы настолько сильно ( 2γa >>1), что можно учитывать только прыжки
между ближайшими ЛС. Электрическое поле напряжённости F0
направлено вдоль оси x. Будем использовать так называемую модель Миллера-Абрахамса (1.59) для частот прыжков. Частоты прыжков поперёк и вдоль поля обозначим как
ν1 = ν→ = ν0 exp(−2γa), а против поля – |
|
ν← = ν0 exp(−2γa −δ)≈ ν1 −ν1δ, δ = eF0a kT . |
(1.65) |
Следует напомнить, что сильная локализация означает экспоненциальную малость интеграла перекрытия, I exp(−2γa) (см.
раздел 1.1). Чтобы исключить делокализованные состояния в этой модельной системе, будем считать, что интеграл перекрытия настолько мал, что критерий Андерсона выполнен, т.е. все состояния локализованы, хотя разброс энергий ЛС E0 настолько мал, что эти
ЛС можно считать изоэнергетическими: I << E0 << eF0a . Пусть числа заполнения всех состояний f малы. Таким образом, уравнение баланса (1.49) принимает следующий вид:
|
|
|
|
|
∂f (x, y, z,t) |
= Γz |
+ Γy + Γx + ΔΓx , |
|
|
|
(1.66) |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
где |
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
( |
|
|
) |
|
( |
|
|
) |
1 |
( |
|
) |
|
( |
|
) |
||
Γ |
x |
x + a, y, z,t |
− f |
x, y, z,t |
x − a, y, z,t |
− f |
x, y, z,t |
||||||||||||
|
= ν f |
|
|
|
+ ν f |
|
|
|
, |
||||||||||
аналогично Γy , Γz – темпы переходов вдоль соответствующих
осей. Электрическое поле влияет на характер движения лишь вдоль оси x . Используя (1.65), получаем
58

ΔΓx = ν1 1−exp(−δ) f (x + a, y, z,t )− f (x, y, z,t ) . (1.67)
Предполагая, что функция f изменяется достаточно плавно вдоль любой из координат, и ограничиваясь первыми неисчезающими членами разложения по длине прыжка a , в предельном случае слабого поля ( δ = eF0a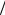 kT <<1 ) из (1.66) получаем дрейфово-
kT <<1 ) из (1.66) получаем дрейфово-
диффузионное уравнение:
|
∂f (x, y, z,t) |
= D |
∂ |
2 |
|
2 |
|
|
|
∂ |
2 |
f −V |
∂f |
|
|
|||
|
|
|
|
+ |
∂ |
+ |
|
|
, |
(1.68) |
||||||||
|
∂t |
∂x |
2 |
|
2 |
∂z |
2 |
∂x |
||||||||||
|
|
|
|
|
∂y |
|
|
|
|
|
|
|||||||
где |
D = ν1a2 ≈ (ν 6)a2 , ν1 |
– характерная частота ухода носителя, |
||||||||||||||||
V = μF0 – скорость дрейфа, |
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|||
|
D μ = a F |
|
1−exp |
−eF a kT |
. |
|
(1.69) |
|||||||||||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0 0 |
) |
|
|
|||
В |
предельном |
случае |
|
|
слабого |
|
|
поля, |
|
δ = eF0a kT <<1 , |
||||||||
1−exp(−δ)≈ δ , так что из (1.69) следует μ = (e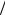 kT )D , то есть со-
kT )D , то есть со-
отношение Эйнштейна выполнено. Однако при конечной длине прыжка это соотношение легко может быть нарушено [1:10, 11]. Действительно, при T= 300 К и a =1 нм δ >1, если
F0 > 2,5 105 В/см. Такие напряжённости обычны как в эксперимен-
тальной практике, так и в органической электронике (благодаря тонкости слоя).
С ростом поля отношение D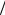 μ возрастает (поскольку прыжки
μ возрастает (поскольку прыжки
против поля подавлены, дрейфовая скорость перестаёт расти с увеличением поля, и подвижность уменьшается), и в обратном случае eF0a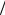 kT >>1 из (1.69) следует D
kT >>1 из (1.69) следует D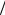 μ ≈ a0 F0 >> kT
μ ≈ a0 F0 >> kT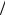 e . Например, при
e . Например, при
F0 =106 В/см и a0 =1 нм D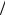 μ = 0,1 B ≈ 4kT
μ = 0,1 B ≈ 4kT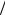 e (при комнатной тем-
e (при комнатной тем-
пературе).
При выводе уравнения (1.69) предполагалась малость производных по координатам, например: a ∂ρ ∂x << ρ , a ∂2ρ
∂x << ρ , a ∂2ρ ∂x2 << ∂ρ
∂x2 << ∂ρ ∂x .
∂x .
Подставив в данные неравенства гауссовское решение уравнения (1.69), нетрудно получить условия применимости сделанного
дрейфово – диффузионного приближения по координате и времени: t >> v1−1 x −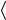 x
x

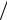 2a , т. е. в ограниченной области пространства применимость данного приближения наступает лишь спустя неко-
2a , т. е. в ограниченной области пространства применимость данного приближения наступает лишь спустя неко-
59
торое время после генерации носителей в виде тонкого слоя. Обобщая (подробнее см. обзор [1:37]), нужно заметить, что на-
рушения соотношения Эйнштейна в неупорядоченных органических материалах связаны: 1) с нелинейными эффектами в достаточно сильных полях, когда выводимая из экспериментальных данных подвижность растёт с ростом поля медленнее, чем коэффициент диффузии; 2) с сильной неравновесностью начального (после генерации) энергетического распределения носителей заряда и 3) с вырождением энергетического распределения носителей, когда их концентрация достаточно высока и, соответственно, высоко нахо-
дится квазиуровень Ферми EF .
1. Эффект конечности длины прыжка, рассмотренный выше, следует отделять от особенностей дрейфа в неупорядоченной среде. Согласно данным времяпролётных экспериментов (см. раздел 2.1) и численного моделирования [1:14], величина D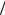 μ в неупоря-
μ в неупоря-
доченных органических материалах возрастает с увеличением напряжённости поля (и степени беспорядка), при этом D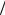 μ при не
μ при не
слишком сильных полях возрастает как F02 и может превышать kT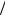 e на несколько порядков величины, т.е. много больше, чем рассмотрено выше, даже при условии eF0a
e на несколько порядков величины, т.е. много больше, чем рассмотрено выше, даже при условии eF0a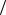 kT <1 . Этот эффект (так
kT <1 . Этот эффект (так
называемая полевая диффузия) вызван случайным разбросом времён освобождения носителей с глубоких ЛС в неупорядоченной среде (он существует и при наличии делокализованных состояний, т.е. не является особенностью прыжкового транспорта, хотя зависимости от параметров могут отличаться) в условиях, когда заселённость ЛС не слишком отличается от равновесной. При этом ещё применимо уравнение, похожее на (1.69). Полевая диффузия (при eF0a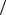 kT <1 ) рассмотрена в гл. 4.
kT <1 ) рассмотрена в гл. 4.
2. В этой же главе рассмотрен и случай сильно неравновесного распределения носителей, когда энергетическая релаксация (а также транспорт) идёт в режиме прыжков вниз по энергии (на начальном временном интервале, длительность которого растёт с уменьшением температуры). В этом случае тем более нет оснований для применимости соотношения Эйнштейна. Отношение коэффициента диффузии к подвижности не зависит от температуры, но зависит
60
