
Красавин Компютерныы практикум в среде МатЛаб 2015
.pdf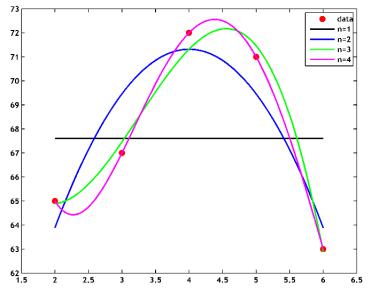
axis([1.5 6.5 62 73])
set(gca, 'LineWidth',1)
set(gca, 'FontName', 'Trebuchet MS') set(gca, 'FontSize', 8)
set(gca, 'FontWeight', 'bold')
Рис. 13.1. Фитирование данных многочленами различной степени
В примере 13.4 рассматривается фитирование данных по численности населения США в различные годы (рис. 13.2).
Пример 13.4.
load census % загрузка данных о численности населения США в различные годы; этот файл поставляется вместе с MatLab
%pop - значения численности начеления,
%cdate - сетка по годам
[p,ErrorEst] = polyfit(cdate,pop,2); % аппроксимация данных многочленом второго порядка
%p – коэффициенты полинома
%ErrorEst - невязка аппроксимации (погрешность)
%вычисление аппроксимированных данных по полученной зависимости
151

[pop_fit,delta] = polyval(p,cdate,ErrorEst);
%pop_fit - аппроксимированные данные
%delta – погрешность
%построение графика численности населения США в различные годы figure
plot(cdate,pop,'d','MarkerSize',8,'MarkerFaceColor','b') hold on
plot(cdate,pop_fit,'g-','LineWidth',2) plot(cdate,pop_fit+3*delta,'r:','LineWidth',2) plot(cdate,pop_fit-3*delta,'r:','LineWidth',2)
xlabel('Годы', 'FontName', 'Trebuchet MS', 'FontSize', 8, 'FontWeight', 'bold');
ylabel('Население (миллионов)', 'FontName', 'Trebuchet MS', 'FontSize', 8,'FontWeight', 'bold');
grid on
legend({'Данные','Фитинг','Погрешность}, 'Location', 'NorthWest') set(gca, 'LineWidth',1)
set(gca, 'FontName', 'Trebuchet MS') set(gca, 'FontSize', 8)
set(gca, 'FontWeight', 'bold')
Рис. 13.2. Фитирование данных численности населения США
152
13.2. Аппроксимация методом наименьших квадратов
В случае, если задана сетка координат |
и вектор значений |
|||||
на этой сетке, то функция lsqcurvefit используется для |
||||||
фитирования |
значений |
|
заданной |
функциональной |
||
зависимостью |
|
|
, где |
|
– параметры функции , |
|
определяемые |
по |
методу наименьших квадратов. Функция |
||||
α, |
|
α |
|
|
||
lsqcurvefit находит значения α , минимизируя выражение |
||||||
|
|
min |
α, |
|
. |
|
Пример 13.5 иллюстрирует использование функции lsqcurvefit для фитирования имеющегося массива данных суммой двух экспонент (рис. 13.3).
Пример 13.5.
% исходные данные
Data = ...
[0.0000 |
5.8955 |
0.1000 |
3.5639 |
0.2000 |
2.5173 |
0.3000 |
1.9790 |
0.4000 |
1.8990 |
0.5000 |
1.3938 |
0.6000 |
1.1359 |
0.7000 |
1.0096 |
0.8000 |
1.0343 |
0.9000 |
0.8435 |
1.0000 |
0.6856 |
1.1000 |
0.6100 |
1.2000 |
0.5392 |
1.3000 |
0.3946 |
1.4000 |
0.3903 |
1.5000 |
0.5474 |
1.6000 |
0.3459 |
1.7000 |
0.1370 |
1.8000 |
0.2211 |
1.9000 |
0.1704 |
2.0000 |
0.2636]; |
t = Data(:,1); % первый столбец данных y = Data(:,2); % второй столбец данных
153

%построение графика зависимости y от t figure
axis([0 2 -0.5 6]) hold on
plot(t,y,'r.','MarkerSize',20)
%Поиск решения с помощью метода наименьших квадратов в виде
%y = c(1)*exp(-lambda(1)*t) + c(2)*exp(-lambda(2)*t), где
%x(1) = c(1)
%x(2) = lambda(1)
%x(3) = c(2)
%x(4) = lambda(2)
%Задаем вид искомой зависимости в форме анонимной функции
F = @(x,xdata)x(1)*exp(-x(2)*xdata) + x(3)*exp(-x(4)*xdata);
x0 = [1 1 1 1]; % начальные значения c(1), lambda(1), c(2) и lambda(2)
x = lsqcurvefit(F,x0,t,y) % метод наименьших квадратов
% построение графика полученной зависимости plot(t,F(x,t),'LineWidth',2)
hold off
set(gca, 'LineWidth',1)
set(gca, 'FontName', 'Trebuchet MS') set(gca, 'FontSize', 8)
set(gca, 'FontWeight', 'bold')
Рис. 13.3. Фитирование данных суммой двух экспонент
154
x =
3.0069 10.5864 2.8890 1.4003
13.3. Сплайны
Сплайном называется кусочно-полиномиальная функция,
определенная |
на отрезке |
, |
и имеющая |
на нем некоторое |
количество |
непрерывных |
производных. |
Сплайны часто |
используются в задаче интерполяции табличных значений функции. На каждом из отрезков между заданными точками координат значения функции интерполируются многочленами определенной степени, которые сшиваются на границах отрезков. В MatLab интерполяция сплайнами (рис. 13.4) осуществляется при помощи функции interp1. В примере 13.6
проиллюстрировано |
использование |
этой |
функции |
для |
интерполяции значений простой функции |
sin |
. |
|
|
Пример 13.6. |
|
|
|
|
x = 0:pi/2:2*pi; % сетка по x |
|
|
|
|
v = sin(x); % вычисление значений синуса на заданной сетке по x xq = 0 : pi/16 : 2*pi; % сетка интерполяции
vq1 = interp1(x,v,xq,'nearest'); % приближение по соседним элементам
vq2 = interp1(x,v,xq); % линейная интерполяция
vq3 = interp1(x,v,xq,'spline'); % интерполяция кубическими сплайнами
vq4 = interp1(x,v,xq,'pchip'); % интерполяция кубическими эрмитовыми сплайнами
% построение результатов интерполяции figure
plot(xq,sin(xq),'Color',[0.1 0.7 1],'LineWidth',2.5) hold on
plot(xq,vq1,'r--','LineWidth',2.5); plot(xq,vq2,'Color',[0.5 0.1 1],'LineWidth',2.5); plot(xq,vq3,'Color','k','LineWidth',2.5); plot(xq,vq4,'Color',[1 0.5 0.1],'LineWidth',2.5); plot(x,v,'o')
axis([0 2*pi -1.1 1.1])
155

box on grid on
legend({'Original','Nearest','Linear','Spline','Pchip'})
set(gca, 'LineWidth',1)
set(gca, 'FontName', 'Trebuchet MS') set(gca, 'FontSize', 8)
set(gca, 'FontWeight', 'bold')
Рис. 13.4. Интерполяция сплайнами
156

14
Частица в потенциальной яме.
Численное решение уравнения Шредингера
14.1. Уравнение Шредингера
Рассмотрим квантово-механическую задачу о движении частицы в потенциальном поле. Квадрат модуля волновой функции |ψ , | для такой системы определяет плотность вероятности обнаружить частицу в момент времени в точке пространства с радиусом-вектором . Временная эволюция функции ψ ,
описывается нестационарным уравнением Шредингера
|
ψ , |
|
|
∆ψ , |
, ψ , , |
|
|
, |
|||||
где – масса частицы; |
– внешнее потенциальное поле. |
|||||
2 |
||||||
Для независящего от времени потенциала решения нестационарного уравнения Шредингера можно искать в виде
ψ , |
|
. |
|
Частица, находящаяся в состоянии, описываемом волновой функцией ψ , , имеет конкретное значение энергии . Подставив ψ , в первое уравнение, получаем стационарное уравнение Шредингера:
2∆
или
,
157

где
2∆
оператор энергии (гамильтониан) системы.
Пусть оператор |
имеет |
собственных функций |
и |
|||
соответствующих им собственных значений энергии |
. Число |
|||||
может быть конечным или бесконечным; значения |
могут быть |
|||||
дискретными |
(дискретный |
спектр) или |
непрерывными |
|||
(непрерывный |
спектр), |
некоторые значения |
могут |
совпадать |
||
(вырожденные состояния), рис. 14.1. Состояние с наименьшей энергией называется основным состоянием системы. Общее решение уравнения Шредингера можно представить в виде суперпозиции собственных функций гамильтониана:
ψ.
Здесь символ ∑ означает суммирование по всем дискретным состояниям и интегрирование по состояниям непрерывного спектра.
Рис. 14.1. Классификация собственных значений оператора энергии
158

14.2. Бесконечная потенциальная яма
Рассмотрим задачу о частице в одномерной потенциальной яме шириной с бесконечно высокими стенками (рис. 14.2).
Рис. 14.2. Бесконечная одномерная потенциальная яма
Гамильтониан этой системы имеет вид
2,
где – масса частицы; |
|
– потенциал ямы, |
|
|
|||||||
|
|
|
0, |
если 0 |
0, |
; |
|
|
|||
Перейдем для удобства к |
∞, |
если |
. |
|
|
||||||
1; |
|
|
безразмерной системе единиц, положив |
||||||||
1, тогда гамильтониан запишется следующим образом: |
|||||||||||
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как потенциал ямы |
бесконечен при |
|
и |
, |
то решение |
||||||
|
|
2 |
|
|
|
|
0в области |
|
|||
уравнения Шредингера существует только |
. |
||||||||||
Подставляя |
выражение |
для гамильтониана |
в |
0уравнение |
|||||||
Шредингера, получаем:
159

|
|
|
|
|
1 |
Ψ |
|
Ψ |
0; |
0 |
, |
. |
1,…,, |
|
|
Разобьем |
|
|
|
, |
|
0 |
|
на |
отрезков |
, |
и |
||||
область2 |
|
|
|
|
|
, |
|||||||||
длиной |
|
/ |
Ψ |
при |
этом |
0; |
;…; |
|
|
|
|
||||
аппроксимируем |
|
|
|
1 |
трехточечной разностной формулой: |
|
|||||||||
|
|
|
Ψ |
|
|
|
Ψ |
2Ψ |
Ψ |
|
, |
|
|
||
тогда получаем: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ψ |
Ψ |
1 |
Ψ |
|
|
|
2Ψ Ψ |
Ψ |
0; |
|
1,…, |
, |
|
|
где |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выберем в качестве ортонормированного базиса систему
функций |
|100…0 ; |
Φ |
|010…0 ; |
… ;Φ |
|000…1 , |
||
где |
Φ |
||||||
|
единица означает, что частица находится на соответствующем |
||||||
отрезке, например, базисная функция |
Φ. |
отвечает ситуации, когда |
|||||
частица находится на |
отрезке |
Размерность этого базиса |
|||||
будет равна числу отрезков разбиения, |
|
. Любая волновая функция |
|||||
Ψможет быть разложена по базисным функциям Φ:
ΨΦ ,
где коэффициенты разложения будут получены далее в расчете, а оператор энергии действует на базисные функции следующим образом:
Φ |
1 |
Φ |
2Φ Φ . |
2 |
|||
|
|
160 |
|
