Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Кудрявтсев Методы оптимизатсии 2015

.pdf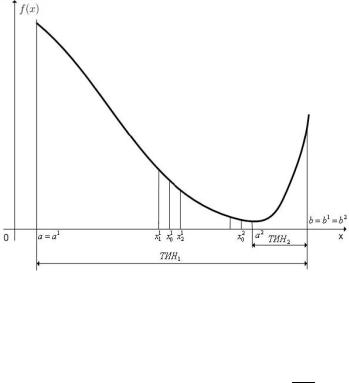

Скачиваний:

Добавлен:

12.11.2022

Размер:

1.51 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Рис. 2.3. Метод дихотомии

Поскольку после каждой итерации длина ТИН уменьшается в два раза, можно априорно оценить количество итераций по задан-

ной точности

решения. Действительно, после

первой

итерации

|ТИН |

после второй итерации |ТИН!|

Но, так как

т.д. Тогда после r-й итерации имеем |ТИН | .

условие окончания поиска |ТИН | + , получаем

+ . За-

менив знак неравенства на равенство и выразив r, получим оценку количества итераций.

Замечание 1. Если производная целевой функции считается достаточно просто, можно видоизменить метод дихотомии. На концах рассматриваемого отрезка вычисляют производные целевой функции, отрезок делят пополам и вычисляют производную в средней точке. Для следующей итерации выбирают тот отрезок из двух получившихся, на концах которого знаки производной различны (по определению унимодальной функции ее производная меняет знак на отрезке поиска только один раз).

Замечание 2. В методе дихотомии на каждой итерации значение функции вычисляется дважды. Однако, как было указано в разделе 1.6, в общем случае стараются уменьшить количество таких вычислений. Поэтому более эффективными являются методы, где новые «экспериментальные» точки на каждой (по возможности) итерации выбираются таким образом, чтобы значение функции приходилось вычислять только один раз.

Метод Фибоначчи

Идея метода Фибоначчи [4] состоит в том, чтобы определять новые «экспериментальные» точки с помощью чисел Фибоначчи,

при этом количество точек фиксировано и равно n. На начальном
	,	,		равен	и извест-
этапе интервал неопределенности длины
но значение функции в точках		!	(рис. 2.4).		2 , 3
				F

Рис. 2.4. Выбор точек в методе Фибоначчи

# и сократить интер-

На следующем этапе надо выбрать точку

2.4). Если

!2,

, 3

! ,

то интервал неопреде-

вал неопределенности. Если

(данный случай изображен на рис.

ленности будет равен

2 , 3

то интервал неопределенности будет ра-

вен

. Точку #

надо выбрать таким образом, чтобы миними-

зировать наибольшую из длин интервалов

. Это

, 3

2 !

длину

интервалов

можно

достигнуть,

обеспечив

одинаковую 2

, 3

симметрично относитель-

! (т.е. поместив точку

но точки

). Таким образом новый интервал неопределенности

2 , 3

равен #

длины

. Рассуждая аналогичным образом, разместим

точку

& симметрично относительно точки

! и получим следующий

интервал неопределенности длины

равный

. На каждом по-

следующем

этапе

требуется

проводить

только

одно вычисление

2 , 3

функции. Следует отметить, что так как новые точки размещаются

симметрично относительно существующей внутренней точки, то, на-

отношение

A F

равна длине интервала ! и,

пример, длина интервала

следовательно,

более общем виде можно записать со-

2!. В, 3

2 , 3

между длинами интервалов неопределенности

На заключительном

этапе для получения интервала неопреде-

A F .

ленности

разместим

точки

(на интервале неопреде-

ленности F

симметрично

относительно середины отрезка и на

расстоянии

ε,

друг от друга, т.е. можно записать, что

A F

ε,

A F

2ε,

A F

3ε.

, 2,

то получимF 1, F 1, F

2, F F

A F

Если ввести обозначения

Полагая

1,2, … , 1.

соотношение

или при

O F

достаточно малым, будем считать

4 1,2, … , 1

O F

Если

O F

4 1,2, … , 1

и тогда

O F

начальный интервал неопределенности

имеет длину

, то после проведения

шагов он станет

равным

2/, 3

(

F ,

т.е. он сократится в

(считая, что значение

является доста-

разF

A ε

точно малым).

Можно заметить, что

F F F F!ε F F

A ε

A F

(

F F F F

Используя

соотноше-

Найдем

выражение

F F

A F F

ние

получим

F F .

F F F

Продолжая подобные преобразования

раз, получим

(

) *

После нахождения

значения

определяется положение первой

A ε

точки для вычисления значения функции. После этого числа Фибоначчи больше не нужны, так как все последующие точки определяются на основе правила симметрии.

Как уже отмечалось, числа Фибоначчи задаются рекуррентным

соотношением

Вычислять

рекуррентным образом можно с помощью вы-

числа ФибоначчиFне F

A F

, 2, F

F 1.

ражения

O 0,618

+, - ) ,*

(2.1)

√

√&

где

(2.2)

– решение квадратного уравнения

Тогда

можно пренебречь.

При больших

значениях i

членом

Q A Q 1 0.

F O

(2.3)

√&

+, -

Можно заметить, что из (2.3) следует

F O √&

и, следова-

тельно,

O Q,

(2.4)

т.е. при больших i отношение двух соседних чисел Фибоначчи примерно постоянно. Q

Следует обратить внимание, что значение иррациональное, а числа Фибоначчи целые. Для вывода соотношения (2.1) рассмот-

рим бесконечный ряд вида

F 1, F 1, F F A F , 2.

— числа ФибоначчиS T ∑ F T

где

Кроме, того введем еще два ряда:

S T ∑/ F T .

S T ∑/

F T

Исходя из рекуррентного соотношения

F F A F , можем

записать:

A F

T F

S T A S T .

S T F A F T A F T A P

Представим ряд S T в

развернутом виде:

A F

A F T

A F T … .

Данное выражение

T F

A F T

может быть записано как

Аналогично получим S T

TF .

T TF

T TS

TF TF

T T

F TF .

T A S

или

A S T

TF TS T TF

Исходя из того, что

, получим

T T

T 1 T

U S

√5 A 1

√5

0 0

Вычисляя корни знаменателя

Q ,

√

Q , T

O 0,618

S T √0& <0 0 0 0 =.

где

представим выражение для

в виде

Используя формулу суммы членов геометрической прогрессии, представим:

W1 A

A P X

T T

;

A :

A P E ;

T C1 A

A :

;

1 W1 A

A <

A P X

T T

X A P ;.

:1 A

A W

X A W

Подставляя указанные выражения в формулу для

, получим

A···;.

√5

Сопоставляя полученное выражение с выражением для ряда

! "! #

# ! "! #

" # ! "! #

найдем, что

√5

, F

√5

, … , F

√5

Алгоритм метода состоит из двух этапов.

2/ ,

Вычисляем величины

ТИН

Первый этап состоит из N-1 итерации для

=1, 2,..., N-1. Рас-

смотрим схему r-й итерации, когда

A |

ТИН

A | ТИН

; в?

/ ,

Вычисляем значения

ТИН

то

Если

выполняем присваивание

противном случае

В обоих

случаях

Данный этап алгоритма обладает тем свойством, что после выполнения N-1 итерации имеет место следующая ситуация:

ТИН

3 ТИН

. Таким образом, на N-1 итерации сужения ТИН не

ТИН

происходит:

причем

точка

оказывается в середине

Второй этап позволяет определить, с какой стороны от точки

свободный

A B

Z | ТИН

лежит точка минимума. Для этого:

Находим точку

, где

–

параметр алгоритма.

ТИН

;

Вычисляем значение

Если

то выполняем присваивание

ТИН

в противном случае

В качестве приближенного значения точки минимума

может

быть принята любая точка последнего ТИН.

Некоторые свойства метода Фибоначчи

Утверждение

1. Для любого r =1, 2,..., N-2 метод Фибоначчи

обладает следующим свойством: одна из точек

совпадает

с одной из точек

2/ , 3

ТИН

Доказательство. Пусть на r-й итерации выполняется

Так

как

A | ТИН

| F

, тогда

Рассмотрим

точку

A | ТИН

то

A </

= F

ТИН | F /

A | ТИН

| F

Доказательство для случая

проводится аналогич-

но. Указанное свойство

позволяет на каждой итерации (кроме пер-

вой) производить испытания только в одной точке.

Утверждение 2. Точки , расположены симметрично отно-

сительно концов ТИН.

/ /

/ / A

Доказательство.

В соответствии с алгоритмом имеем:

/ /

/ W1

/ WF

Фибоначчи следует, что

Так как из определения чиселF

, второе выражение можно записать

как F

. Отсюда получаем, что

Утверждение 3. В результате любой итерации r =1, 2,..., N - 2

длина ТИН уменьшается в

раз.

Доказательство. Из утверждения 2

следует,

что

3, 2

отрез-

поэтому достаточно рассмотреть только один

из /

/ / A / FF

/ / FF

ков

. Рассмотрим первый отрезок:

Утверждение 4. Из утверждения 3 и (2.4) следует, что при достаточно больших N в результате одной итерации длина ТИН уменьшается в τ раз.

Утверждение 5. В результате						N итераций длина ТИН стано-
вится равной				.
		1
после второй итерации \| ТИН \| / 1 ,
Доказательство. Действительно, после первой итерации
\| ТИН!\| / Y						Y	1
							/ Y

и т.д.; после	N-		2 итерации		имеем	Y		Y
					Y
					28

после 1

| ТИН

| /

N- итерации длина ТИН не меняется, после N-й итерации

) *

длина ТИН уменьшается ровно в два раза (так как из утверждения

2 и выражения

делит ТИН

следует, что

Метод | ТИН |

пополам):

Фибоначчи является достаточно эффективным (см. раздел 2.1.3) методом одномерной оптимизации, однако в нем доставляет неудобство тот факт, что после выбора значения параметра N следует обязательно сделать N-1 итераций, без возможности остановки даже в том случае, когда длина очередного ТИН стала меньше заданной точности решения. От этого недостатка можно избавиться следующим образом: из (2.4) следует, что отношение соседних чисел Фибоначчи примерно постоянно, следовательно, на каждой итерации можно выбирать экспериментальные точки так, чтобы они делили ТИН в одном и том же отношении τ, которое не зависит от N. Эти рассуждения ложатся в основу метода золотого сечения.

Метод золотого сечения

Метод золотого сечения является почти таким же эффективным, как метод Фибоначчи, но позволяет остановить вычисления на любой итерации [4]. Определение золотого сечения дается следующим образом: говорят, что точка c выполняет золотое сечение от-


резка [a, b], если 2		Q		.	Кроме того из определения золотого се-
чения следует, что		Q			Кроме того из определения золотого се-
			)			1	1 Q.
	2		)		)2	2

После того как выполнено j шагов, будет получен интервал неопределенности, для которого справедливо соотношение

							.
Так как при золотом		сечении отрезка отношение интервалов посто-
		F	F	F	F A F
янное и равное Q, то						F
		можно записать:
								P Q
и	F			F		F

						29

1 A

1 A Q.

O 0,618

из решения уравнения

Откуда Q находится

A Q 1 0

√

. Исходя из полученного, можно записать:

Q ,

и т.д. Следовательно, после выполнения n шагов интервал неопре-

lim

. Поскольку

деленности становится равным

что поиск методом золотого сечения

, то можно сказать,F

· Q

является предельной формой поиска метода Фибоначчи.

Алгоритм метода:

2/ , 3

4 1, /

/, , ТИН

Выполняем присваивание

/ · Q.

· Q,

/ A

Вычисляем величины

Если

;

Вычисляем значения

то выполняем присваивание

в противном случае

/ ,

ТИН

|ТИН

| +

В обоих случаях

Если

, то заканчиваем вычисления; иначе вы-

полняем присваивание r = r+1 и переходим к шагу 2.

В качестве приближенного значения точки минимума

может

быть принята любая точка последнего ТИН.

Некоторые свойства метода золотого сечения

Утверждение 1. Для любого r ≥ 1 метод золотого сечения об-

ладает следующим свойством: одна из точек

совпадает с

. Чтобы

одной из точек

2/ , 3

ТИН

Доказательство.

Пусть на

-й итерации выполняется

, тогда

доказать

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.20222.92 Mб1Кувяткина Международные стандарты учета и отчетности 2012.pdf
#
12.11.202210.45 Mб26Кудинова Практическиы курс аглиыского языка для студентов международник Ч.1 2014.pdf
#
12.11.202210.79 Mб22Кудинова Практическиы курс англиыского языка для студентов международник Ч.2 2014.pdf
#
12.11.202212.14 Mб28Кудинова Практическиы курс англиыского языка для студентов международник Ч.3 2014.pdf
#
12.11.202210.38 Mб14Кудинова Практическиы курс англиыского языка для студентов международник Ч.4 2014.pdf
#
12.11.20221.51 Mб12Кудрявтсев Методы оптимизатсии 2015.pdf
#
12.11.20221.39 Mб7Кузмина, Что такое ядерная медецина 20112.pdf
#
12.11.2022688.18 Кб5Кушин Методы регистратсии излучениы 2015.pdf
#
12.11.20222.76 Mб8Лабораторный практикум Атомная физика.pdf
#
12.11.20221.65 Mб2Лабораторный практикум Конструкционные материалы ядерных реакторов.pdf
#
12.11.20224.42 Mб4Лабораторный практикум курса общей физики. Раздел Атомная физика.pdf