
ЛР4_КОЭД_Шакиров_Ибрагимова_МО417
.docxМинистерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Уфимский государственный авиационный технический университет»
Кафедра вычислительной математики и кибернетики
Лабораторная работа №4
«Прогнозирование временных рядов»
по дисциплине:
«Компьютерная обработка экспериментальных данных»
Выполнили:
студенты группы МО-417
Ибрагимова К.Б.
Шакиров А.Р.
Проверила:
Харисова Э.А.
Уфа 2022
Задание и порядок выполнения работы:
Загрузить N значений временного ряда, соответственно варианту. Для данной выборки найти оценки математического ожидания и дисперсии. Построить график xt = (t), t=1, 2, …, N полученных значений временного ряда.
Использовать постоянную модель (n=0) для прогнозирования значений временного ряда при = 0,1 и = 0,3. St1 считать прогнозом на момент времени t+1. Начальное значение S01 найти как среднее арифметическое пяти первых значений временного ряда. На каждом шаге сравнить предсказанное xtˆ и действительное xt значения, выписывая ошибку предсказания xt = xt - xtˆ, t=1, 2, …, N. Вычислить дисперсию s2[xtˆ] ошибки предсказания по данным эксперимента.
Оценить начальные значения коэффициентов линейной модели A0(0) и A1(0), воспользовавшись методом наименьших квадратов, то есть по значениям xt = (t) нужно построить аппроксимирующую прямую. Точка пересечения этой линии с осью ординат определяет величину A0(0), а тангенс угла наклона к оси абсцисс – величину A1(0).
Используя операторы экспоненциального сглаживания первого и второго порядков (пункт «Многократное экспоненциальное сглаживание»), получить сглаженные значения St1 и St2, t=1, 2, …, N при значениях постоянной сглаживания = 0,1 и = 0,3. Построить графики (всего четыре графика).
Использовать линейную модель (n=1) для прогнозирования значений временного ряда х с интервалом упреждения τ =∆t, что равносильно m=1 при = 0,1 и = 0,3. На каждом шаге сравнить предсказанное xtˆ и действительное xt значения, выписывая ошибку предсказания xt = xt - xtˆ, t=1, 2, …, N. Вычислить дисперсию ошибки предсказания по данным эксперимента s2[xtˆ].
Выполнить пункт 5) для m=5.
Представить рекомендацию по выбору модели (порядка полинома) для заданного временного ряда по приведенному в пункте «Выбор модели» алгоритму.
Ход работы:
Загрузим 30 значений временного ряда, соответственно варианту 10.

Рисунок 1 – Исходные данные
Для данной выборки найдем оценки математического ожидания и дисперсии.

Рисунок 2 – Оценки математического ожидания и дисперсии
Построим график xt = (t), t=1, 2, …, 30 полученных значений временного ряда.

Рисунок 3 – График значений временного ряда
Используем постоянную модель (n=0) для прогнозирования значений временного ряда при = 0,1.
St1 будем считать прогнозом на момент времени t+1. Начальное значение S01 найдем как среднее арифметическое пяти первых значений временного ряда. С помощью рекуррентной формулы рассчитаем следующие значения:
![]()
На каждом шаге сравним предсказанное xtˆ и действительное xt значения, выписывая ошибку предсказания xt = xt - xtˆ, t=1, 2, …, N.

Рисунок 4 – Прогнозные значения St1 и ошибка предсказания xt
Вычислим дисперсию s2[xtˆ] ошибки предсказания по данным эксперимента по формуле:

![]()
Рисунок 5 – Дисперсия ошибки предсказания s2[xtˆ]
Проделаем аналогичные вычисления при = 0,3.

Рисунок 6 – Прогнозирование значений временного ряда
Оценим начальные значения коэффициентов линейной модели A0(0) и A1(0), воспользовавшись методом наименьших квадратов.
По значениям xt = (t) построим аппроксимирующую прямую. Точка пересечения этой линии с осью ординат определяет величину A0(0), а тангенс угла наклона к оси абсцисс – величину A1(0).
Найдем значения a1 и a0 по формулам:


![]()
Рисунок 7 – Коэффициенты уравнения
Найдем зависимость вида y = a0 + a1*x.

Рисунок 8 – Зависимость вида y = 33,5333 + 1,2*x
Построим аппроксимирующую прямую.

Рисунок 9 – Аппроксимирующая прямая
Используя операторы экспоненциального сглаживания первого и второго порядков, получим сглаженные значения St1 и St2, t=1, 2, …, N при значениях постоянной сглаживания = 0,1 и = 0,3.
Получим сглаженные значения St1 и St2 при постоянной сглаживания = 0,1. Начальные значения получим по формулам:


Рисунок 10 – Сглаженные значения St1 и St2 при постоянной сглаживания = 0,1
Получим сглаженные значения St1 и St2 при постоянной сглаживания = 0,3.

Рисунок 11 – Сглаженные значения St1 и St2 при постоянной сглаживания = 0,3
Построим графики сглаженных значений.

Рисунок 12 – Сглаженные значения
Используем линейную модель (n=1) для прогнозирования значений временного ряда х с интервалом упреждения τ =∆t, что равносильно m=1 при = 0,1.
Найдем коэффициенты линейной модели по формулам:

На каждом шаге будем сравнивать предсказанное xtˆ и действительное xt значения, выписывая ошибку предсказания xt = xt - xtˆ, t=1, 2, …, N.

Рисунок 13 – Коэффициенты линейной модели и ошибка предсказания xt
После того как получим оценки коэффициентов модели, вычислим оценку будущего наблюдения:
При m = 1, n = 1 формула вида

примет вид
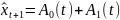
и вычислим дисперсию s2[xtˆ] ошибки предсказания по данным эксперимента:

![]()
Рисунок 14 – Оценка будущего наблюдения и дисперсия s2[xtˆ]
ошибки предсказания при m=1
Проделаем аналогичные вычисления при = 0,3.

Рисунок 15 – Вычисления при = 0,3
Выполним предыдущий пункт при m=5.
При m = 5, n = 1 формула вида
примет вид

При = 0,1

Рисунок 16 – Вычисления при m=5 и = 0,1
При = 0,3

Рисунок 17 – Вычисления при m=5 и = 0,3
Дисперсия ошибки предсказания s2[xtˆ] при m=5 увеличилась по сравнению с дисперсией ошибки предсказания при m=1.
Для определения порядка полинома на основе выборки вычислим разности первого порядка ∆x(t) = xt+1 — xt. Если среднее разностей (п-1)-го порядка отлично от нуля, а среднее разностей n-го порядка равно нулю, то моделью служит полином (n—1)-й степени
При подборе модели опишем не весь ряд целиком, так как модель должна хорошо представлять лишь некоторый отрезок.

Рисунок 18 – Выбор модели (порядка полинома)
Так как среднее разностей 1-порядка равно нулю, то моделью служит полином нулевого порядка, т. е. константа.
Вывод
В ходе выполнения лабораторной работы были изучены методы прогнозирования значений временного ряда.
