
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ИНФОРМАТИКИ И РОБОТОТЕХНИКИ
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И КИБЕРНЕТИКИ
|
|
|
||
|
УТВЕРЖДАЮ Проректор университета по научной работе ФИО |
|||
|
|
|
||
|
"___" ______________ _______г. |
|||
|
|
|
||
ОТЧЕТ О ПРОВЕДЕНИИ ЛАБОРАТОРНОЙ РАБОТЫ № 2 «Точечные оценки параметров методом моментов» |
||||
|
||||
по предмету: Статистическое моделирование |
||||
Преподаватель |
|
Е.Ю. Сазонова |
||
|
|
|
||
|
|
|
||
|
|
|
||
Исполнители |
|
К.Б. Ибрагимова А.Р. Шакиров |
||
Уфа 2021
Лабораторная работа №2
Ибрагимова, Шакиров
14.04.2021
Точечные оценки параметров методом моментов.
Сгенерируем выборки. x1 - с нормальным распределением, x2 - с показательным, x3 - с биномиальным.
set.seed(0) a_real <- 16 si_real <- 24 x1 <- rnorm(628, a_real, si_real) lam_real <- 8 x2 <- rexp(600, lam_real) size.binom <- 27 prob.binom <- 0.6 np_real <- size.binom*prob.binom x3 <- rbinom(600, size.binom, prob.binom) str(x1)
## num [1:628] 46.31 8.17 47.92 46.54 25.95 ...
str(x2)
## num [1:600] 0.23085 0.14893 0.00155 0.00664 0.06357 ...
str(x3)
## int [1:600] 17 18 20 14 16 20 17 17 18 18 ...
Найдем оценки неизвестных параметров Теоретические моменты для нормального закона распределения - a (коэффициент сдвига), σ (коэффициент масштаба)
Точечные оценки параметров нормального распределения: a = математическое ожидание нормального распределения σ = среднеквадратическое отклонение нормального распределения
a <- mean(x1) si <- sd(x1) cat(sprintf("для нормального закона распределения: a = %f и si = %f \n", a, si ))
## для нормального закона распределения: a = 15.523792 и si = 23.773510
cat(sprintf("отличается от заданного a на %f, от заданного σ на %f", abs(a - a_real), abs(si - si_real) ))
## отличается от заданного a на 0.476208, от заданного <U+03C3> на 0.226490
Теоретические моменты для показательного закона распределения - 1/λ
Точечные оценки параметров показательного распределения: λ = 1 / математическое ожидание
lam <- 1/mean(x2) cat(sprintf("для показательного закона распределения: lam = %f\n", lam ))
## для показательного закона распределения: lam = 7.584327
cat(sprintf("отличается от заданного на %f\n", abs(lam - lam_real) ))
## отличается от заданного на 0.415673
Теоретические моменты для биномиального закона распределения - np
Точечные оценки параметров показательного распределения: p = математическое ожидание / кол-во успехов n = математическое ожидание / вероятность успеха
p <- mean(x3)/size.binom; #27 n <- mean(x3)/prob.binom; #0.6 np <- n*p cat(sprintf("для биномиального закона распределения: np = %f\n", np ))
## для биномиального закона распределения: np = 16.313532
cat(sprintf("отличается от заданного на %f\n", abs(np - size.binom*prob.binom) ))
## отличается от заданного на 0.113532
Точечные оценки являются достаточно точными.
Реализация нахождения оценок на сгенерированной выборке
Создадим 20 выборок с n=10, распределенной по НЗР:
n <- 10 varCount <- 20 a_real <- 16 si_real <- 24 xs <- rnorm(n * varCount, a_real, si_real) M <- matrix (xs , varCount , n)
Вычислим значения оценок и посмотрим получившиеся векторы оценок.
method.moment <- function (x) (2/n) * sum(x) method.max_likely <- function (x) ((n+1) /n ) * max(x) method.ordinal_stats <- function (x) (2 * quantile(x , c(0.5)))
rez1 <- apply(M, 1, method.moment) rez2 <- apply(M, 1, method.max_likely) rez3 <- apply(M, 1, method.ordinal_stats) str(rez1)
## num [1:20] 18.4 60.7 27.4 19.6 41 ...
str(rez2)
## num [1:20] 53.9 66.6 43.4 48.5 73.4 ...
str(rez3)
## num [1:20] 22.2 65.8 41.6 28.5 29.4 ...
Отобразим получившиеся значения на графике:
vecmax<-c(max(max(rez1),max(rez2),max(rez3))) vecmin<-c(min(min(rez1),min(rez2),min(rez3))) plot(rez1, col = "red", ylim = c(vecmin, vecmax)) lines(rez1, col = "red", ylim = c(vecmin, vecmax)) par(new=T) plot(rez2 , col = "blue", ylim = c(vecmin, vecmax)) lines(rez2 , col = "blue", ylim = c(vecmin, vecmax)) par(new=T) plot(rez3 , col = "green", ylim = c(vecmin, vecmax)) lines(rez3 , col = "green", ylim = c(vecmin, vecmax))

par(new=F)
Вычислим среднеквадратическое отклонение, максимальное и минимальное значение, величину размаха:
p11 <- sd(rez1) p12 <- sd(rez2) p13 <- sd(rez3) pN10 <- c(p11,p12,p13) max1 <- max(rez1) max2 <- max(rez2) max3 <- max(rez2) maxN10 <- c(max1,max2,max3) min1 <- min(rez1) min2 <- min(rez2) min3 <- min(rez2) minN10 <- c(min1,min2,min3) R1<-max1-min1 R2<-max2-min2 R3<-max3-min3 RN10 <- c(R1,R2,R3) tabN10 = data.frame( sd = c(p11, p12, p13), max = c(max1, max2, max3), min = c(min1, min2, min3), r = c(R1, R2, R3) ) tabN10
## sd max min r ## 1 17.16001 68.62087 7.795118 60.82575 ## 2 13.36537 85.86603 37.659836 48.20619 ## 3 19.28662 85.86603 37.659836 48.20619
Отобразим на сколько отличается оценка от заданного параметра
plot(abs(rez1 - si_real), col = "red", main = "Δsi (метод моментов)") lines(abs(rez1 - si_real), col = " red")

plot(abs(rez2 - si_real), col = "blue", main = "Δsi (метод максимального правдоподобия)") lines(abs(rez2 - si_real) , col = "blue")

plot(abs(rez3 - si_real), col = "green", main = "Δsi (метод порядковых статистик)") lines(abs(rez3 - si_real), col = "green")

Метод моментов показывается наиболее точным.
Создадим 20 выборок с n=40, распределенной по НЗР:
n <- 40 varCount <- 20 xs <- rnorm (n* varCount, a_real, si_real) M <- matrix (xs , varCount , n)
Вычислим значения оценок и посмотрим получившиеся векторы оценок.
rez1 <- apply(M, 1, method.moment) rez2 <- apply(M, 1, method.max_likely) rez3 <- apply(M, 1, method.ordinal_stats) str(rez1)
## num [1:20] 26.2 45.2 28.1 26.5 41.7 ...
str(rez2)
## num [1:20] 52.8 69.9 88.2 44.8 84.8 ...
str(rez3)
## num [1:20] 31.1 46.3 19 31.3 25.2 ...
Отобразим получившиеся значения на графике:
vecmax<-c(max(max(rez1),max(rez2),max(rez3))) vecmin<-c(min(min(rez1),min(rez2),min(rez3))) plot ( rez1 , col = " red ", ylim = c(vecmin, vecmax)) lines ( rez1 , col = " red", ylim = c(vecmin, vecmax)) par ( new =T ) plot ( rez2 , col = " blue ", ylim = c(vecmin, vecmax)) lines ( rez2 , col = " blue ", ylim = c(vecmin, vecmax)) par ( new =T ) plot ( rez3 , col = " green ", ylim = c(vecmin, vecmax)) lines ( rez3 , col = " green ", ylim = c(vecmin, vecmax))

par ( new =F )
Вычислим среднеквадратическое отклонение, максимальное и минимальное значение, величину размаха:
p11 <- sd( rez1 ) p12 <- sd( rez2 ) p13 <- sd( rez3 ) pN40 <- c(p11,p12,p13) max1 <- max( rez1) max2 <- max( rez2) max3 <- max( rez2) maxN40 <- c(max1,max2,max3) min1 <- min( rez1) min2 <- min( rez2) min3 <- min( rez2) minN40 <- c(min1,min2,min3) R1<-max1-min1 R2<-max2-min2 R3<-max3-min3 RN40 <- c(R1,R2,R3) tabN40 = data.frame(sd = c(p11, p12, p13), max = c(max1, max2, max3), min = c(min1, min2, min3), r = c(R1, R2, R3)) tabN40
## sd max min r ## 1 8.373561 49.02938 17.44370 31.58567 ## 2 12.078280 93.98770 44.84408 49.14362 ## 3 10.930758 93.98770 44.84408 49.14362
Отобразим на сколько отличается оценка от заданного параметра
plot(abs(rez1 - si_real), col = "red", main = "Δsi (метод моментов)") lines(abs(rez1 - si_real), col = " red")

plot(abs(rez2 - si_real), col = "blue", main = "Δsi (метод максимального правдоподобия)") lines(abs(rez2 - si_real) , col = "blue")

plot(abs(rez3 - si_real), col = "green", main = "Δsi (метод порядковых статистик)") lines(abs(rez3 - si_real), col = "green")

Метод моментов показывается наиболее точным.
Создадим 20 выборок с n=160, распределенной по НЗР:
n <- 160 varCount <- 20 xs <- rnorm (n* varCount, a_real, si_real) M <- matrix (xs , varCount , n)
Вычислим значения оценок и посмотрим получившиеся векторы оценок.
rez1 <- apply(M, 1, method.moment) rez2 <- apply(M, 1, method.max_likely) rez3 <- apply(M, 1, method.ordinal_stats) str(rez1)
## num [1:20] 29.8 30.7 29.1 37.9 31.5 ...
str(rez2)
## num [1:20] 92.8 85.2 68.7 67.5 64.2 ...
str(rez3)
## num [1:20] 28.1 30.9 32 46.5 33.9 ...
Отобразим получившиеся значения на графике:
vecmax<-c(max(max(rez1),max(rez2),max(rez3))) vecmin<-c(min(min(rez1),min(rez2),min(rez3))) plot ( rez1 , col = " red ", ylim = c(vecmin, vecmax)) lines ( rez1 , col = " red", ylim = c(vecmin, vecmax)) par ( new = T ) plot ( rez2 , col = " blue ", ylim = c(vecmin, vecmax)) lines ( rez2 , col = " blue ", ylim = c(vecmin, vecmax)) par ( new = T ) plot ( rez3 , col = " green ", ylim = c(vecmin, vecmax)) lines ( rez3 , col = " green ", ylim = c(vecmin, vecmax))

par ( new = F )
Отобразим на сколько отличается оценка от заданного параметра
plot(abs(rez1 - si_real), col = "red", main = "Δsi (метод моментов)") lines(abs(rez1 - si_real), col = " red")

plot(abs(rez2 - si_real), col = "blue", main = "Δsi (метод максимального правдоподобия)") lines(abs(rez2 - si_real) , col = "blue")

plot(abs(rez3 - si_real), col = "green", main = "Δsi (метод порядковых статистик)") lines(abs(rez3 - si_real), col = "green")

Метод моментов показывается наиболее точным.
Вычислим среднеквадратическое отклонение, максимальное и минимальное значение, величину размаха:
p11 <- sd( rez1 ) p12 <- sd( rez2 ) p13 <- sd( rez3 ) pN160 <- c(p11,p12,p13) max1 <- max( rez1) max2 <- max( rez2) max3 <- max( rez2) maxN160 <- c(max1,max2,max3) min1 <- min( rez1) min2 <- min( rez2) min3 <- min( rez2) minN160 <- c(min1,min2,min3) R1<-max1-min1 R2<-max2-min2 R3<-max3-min3 RN160 <- c(R1,R2,R3) tabN160 = data.frame( sd = c(p11, p12, p13), max = c(max1, max2, max3), min = c(min1, min2, min3), r = c(R1, R2, R3) ) tabN160
## sd max min r ## 1 4.693123 41.12446 23.14060 17.98387 ## 2 9.109022 92.84680 57.76678 35.08002 ## 3 5.369449 92.84680 57.76678 35.08002
Сравним минимальные и максимальные величины, величину размаха, среднеквадратическое отклонение между оценками для выборок объема 10,40,160 для НЗР.
id <- c("метод моментов для n = 10", "метод максимального правдоподобия для n = 10", "метод порядковых статистик для n = 10", "метод моментов для n = 40", "метод максимального правдоподобия для n = 40", "метод порядковых статистик для n = 40", "метод моментов для n = 160", "метод максимального правдоподобия для n = 160", "метод порядковых статистик для n = 160") p <- c(pN10,pN40,pN160) max <- c(maxN10,maxN40,maxN160) min <- c(minN10,minN40,minN160) R <- c(RN10,RN40,RN160) tableNZR <- data.frame(N = id, sd = p, Max = max, Min = min, R = R) tableNZR
## N sd Max Min ## 1 метод моментов для n = 10 17.160011 68.62087 7.795118 ## 2 метод максимального правдоподобия для n = 10 13.365367 85.86603 37.659836 ## 3 метод порядковых статистик для n = 10 19.286619 85.86603 37.659836 ## 4 метод моментов для n = 40 8.373561 49.02938 17.443702 ## 5 метод максимального правдоподобия для n = 40 12.078280 93.98770 44.844080 ## 6 метод порядковых статистик для n = 40 10.930758 93.98770 44.844080 ## 7 метод моментов для n = 160 4.693123 41.12446 23.140599 ## 8 метод максимального правдоподобия для n = 160 9.109022 92.84680 57.766780 ## 9 метод порядковых статистик для n = 160 5.369449 92.84680 57.766780 ## R ## 1 60.82575 ## 2 48.20619 ## 3 48.20619 ## 4 31.58567 ## 5 49.14362 ## 6 49.14362 ## 7 17.98387 ## 8 35.08002 ## 9 35.08002
Сравним графически среднеквадратические отклонения трех оценок для значений n=10, n=40 и n=160 для НЗР.
plot (pN10 , col = " red") lines (pN10 , col = " red")

plot (pN40 , col = " blue") lines (pN40 , col = " blue")

plot (pN160 , col = " green") lines (pN160 , col = " green")
 Среднеквадратичное отклонение
с увеличением n уменьшается.
Среднеквадратичное отклонение
с увеличением n уменьшается.
Создадим 20 выборок с n=10, распределенной по ЭЗР:
n <- 10 varCount <- 20 lam_real <- 8 xs <- rexp(n* varCount, lam_real) M <- matrix (xs , varCount , n)
Вычислим значения оценок и посмотрим получившиеся векторы оценок.
rez1 <- apply(M, 1, method.moment) rez2 <- apply(M, 1, method.max_likely) rez3 <- apply(M, 1, method.ordinal_stats) str(rez1)
## num [1:20] 0.303 0.578 0.109 0.249 0.184 ...
str(rez2)
## num [1:20] 0.464 0.788 0.142 0.459 0.398 ...
str(rez3)
## num [1:20] 0.2267 0.5148 0.0766 0.1141 0.1466 ...
Отобразим получившиеся значения на графике:
vecmax<-c(max(max(rez1),max(rez2),max(rez3))) vecmin<-c(min(min(rez1),min(rez2),min(rez3))) plot ( rez1 , col = " red ", ylim = c(vecmin, vecmax), main="1/lam") lines ( rez1 , col = " red", ylim = c(vecmin, vecmax)) par ( new =T ) plot ( rez2 , col = " blue ", ylim = c(vecmin, vecmax)) lines ( rez2 , col = " blue ", ylim = c(vecmin, vecmax)) par ( new =T ) plot ( rez3 , col = " green ", ylim = c(vecmin, vecmax)) lines ( rez3 , col = " green ", ylim = c(vecmin, vecmax))

par ( new =F )
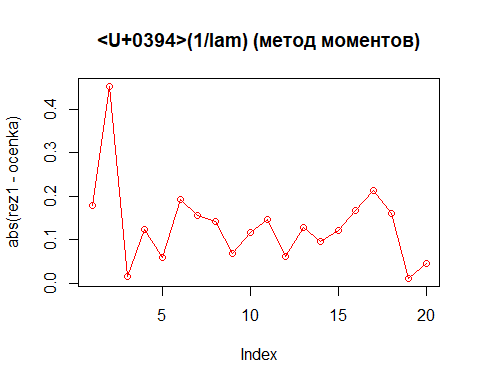
Отобразим на сколько отличается оценка от заданного параметра
ocenka <- 1/lam_real plot(abs(rez1 - ocenka), col = "red", main = "Δ(1/lam) (метод моментов)") lines(abs(rez1 - ocenka), col = "red")
plot(abs(rez2 - ocenka), col = "blue", main = "Δ(1/lam) (метод максимального правдоподобия)") lines(abs(rez2 - ocenka), col = "blue")

plot(abs(rez3 - ocenka), col = "green", main = "Δ(1/lam) (метод порядковых статистик)") lines(abs(rez3 - ocenka), col = "green")

Метод порядковых статистик показывается наиболее точным.
Вычислим среднеквадратическое отклонение, максимальное и минимальное значение, величину размаха:
p11 <- sd( rez1 ) p12 <- sd( rez2 ) p13 <- sd( rez3 ) pN10 <- c(p11,p12,p13) max1 <- max( rez1) max2 <- max( rez2) max3 <- max( rez2) maxN10 <- c(max1,max2,max3) min1 <- min( rez1) min2 <- min( rez2) min3 <- min( rez2) minN10 <- c(min1,min2,min3) R1<-max1-min1 R2<-max2-min2 R3<-max3-min3 RN10 <- c(R1,R2,R3) tabeN10 <- data.frame( sd = c(p11, p12, p13), max = c(max1, max2, max3), min = c(min1, min2, min3), r = c(R1, R2, R3) ) tabeN10
## sd max min r ## 1 0.09676093 0.5775761 0.1094630 0.4681131 ## 2 0.19709799 0.9706065 0.1422553 0.8283513 ## 3 0.09920512 0.9706065 0.1422553 0.8283513
Создадим 20 выборок с n=40, распределенной по ЭЗР:
n <- 40 varCount <- 20 xs <- rexp(n* varCount, lam_real) M <- matrix(xs , varCount , n)
Вычислим значения оценок и посмотрим получившиеся векторы оценок.
rez1 <- apply(M, 1, method.moment) rez2 <- apply(M, 1, method.max_likely) rez3 <- apply(M, 1, method.ordinal_stats) str(rez1)
## num [1:20] 0.214 0.258 0.267 0.251 0.275 ...
str(rez2)
## num [1:20] 0.551 0.921 0.76 0.4 0.576 ...
str(rez3)
## num [1:20] 0.175 0.183 0.129 0.153 0.174 ...
Отобразим получившиеся значения на графике:
vecmax<-c(max(max(rez1),max(rez2),max(rez3))) vecmin<-c(min(min(rez1),min(rez2),min(rez3))) plot ( rez1 , col = " red ", ylim = c(vecmin, vecmax)) lines ( rez1 , col = " red", ylim = c(vecmin, vecmax)) par ( new =T ) plot ( rez2 , col = " blue ", ylim = c(vecmin, vecmax)) lines ( rez2 , col = " blue ", ylim = c(vecmin, vecmax)) par ( new =T ) plot ( rez3 , col = " green ", ylim = c(vecmin, vecmax)) lines ( rez3 , col = " green ", ylim = c(vecmin, vecmax))

par ( new =F )
Отобразим на сколько отличается оценка от заданного параметра
ocenka <- 1/lam_real plot(abs(rez1 - ocenka), col = "red", main = "Δ(1/lam) (метод моментов)") lines(abs(rez1 - ocenka), col = "red")

plot(abs(rez2 - ocenka), col = "blue", main = "Δ(1/lam) (метод максимального правдоподобия)") lines(abs(rez2 - ocenka), col = "blue")

plot(abs(rez3 - ocenka), col = "green", main = "Δ(1/lam) (метод порядковых статистик)") lines(abs(rez3 - ocenka), col = "green")

Метод порядковых статистик показывается наиболее точным.
Вычислим среднеквадратическое отклонение, максимальное и минимальное значение, величину размаха:
p11 <- sd( rez1 ) p12 <- sd( rez2 ) p13 <- sd( rez3 ) pN40 <- c(p11,p12,p13) max1 <- max( rez1) max2 <- max( rez2) max3 <- max( rez2) maxN40 <- c(max1,max2,max3) min1 <- min( rez1) min2 <- min( rez2) min3 <- min( rez2) minN40 <- c(min1,min2,min3) R1<-max1-min1 R2<-max2-min2 R3<-max3-min3 RN40 <- c(R1,R2,R3) tabeN40 <- data.frame(sd = c(p11, p12, p13), max = c(max1, max2, max3), min = c(min1, min2, min3), r = c(R1, R2, R3)) tabeN40
## sd max min r ## 1 0.03572868 0.3120266 0.1688482 0.1431784 ## 2 0.16309205 0.9209055 0.2512482 0.6696572 ## 3 0.03149770 0.9209055 0.2512482 0.6696572
Создадим 20 выборок с n=160, распределенной по ЭЗР:
n <- 160 varCount <- 20 xs <- rexp(n* varCount, lam_real) M <- matrix (xs , varCount , n)
Вычислим значения оценок и посмотрим получившиеся векторы оценок.
rez1 <- apply(M, 1, method.moment) rez2 <- apply(M, 1, method.max_likely) rez3 <- apply(M, 1, method.ordinal_stats) str(rez1)
## num [1:20] 0.251 0.26 0.233 0.265 0.256 ...
str(rez2)
## num [1:20] 0.597 0.622 0.836 0.96 0.686 ...
str(rez3)
## num [1:20] 0.155 0.182 0.164 0.17 0.198 ...
Отобразим получившиеся значения на графике:
vecmax<-c(max(max(rez1),max(rez2),max(rez3))) vecmin<-c(min(min(rez1),min(rez2),min(rez3))) plot ( rez1 , col = " red ", ylim = c(vecmin, vecmax)) lines ( rez1 , col = " red", ylim = c(vecmin, vecmax)) par ( new =T ) plot ( rez2 , col = " blue ", ylim = c(vecmin, vecmax)) lines ( rez2 , col = " blue ", ylim = c(vecmin, vecmax)) par ( new =T ) plot ( rez3 , col = " green ", ylim = c(vecmin, vecmax)) lines ( rez3 , col = " green ", ylim = c(vecmin, vecmax))

par ( new =F )
Отобразим на сколько отличается оценка от заданного параметра
ocenka <- 1/lam_real plot(abs(rez1 - ocenka), col = "red", main = "Δ(1/lam) (метод моментов)") lines(abs(rez1 - ocenka), col = "red")

plot(abs(rez2 - ocenka), col = "blue", main = "Δ(1/lam) (метод максимального правдоподобия)") lines(abs(rez2 - ocenka), col = "blue")

plot(abs(rez3 - ocenka), col = "green", main = "Δ(1/lam) (метод порядковых статистик)") lines(abs(rez3 - ocenka), col = "green")

Метод порядковых статистик показывается наиболее точным.
Вычислим среднеквадратическое отклонение, максимальное и минимальное значение, величину размаха:
p11 <- sd( rez1 ) p12 <- sd( rez2 ) p13 <- sd( rez3 ) pN160 <- c(p11,p12,p13) max1 <- max( rez1) max2 <- max( rez2) max3 <- max( rez2) maxN160 <- c(max1,max2,max3) min1 <- min( rez1) min2 <- min( rez2) min3 <- min( rez2) minN160 <- c(min1,min2,min3) R1<-max1-min1 R2<-max2-min2 R3<-max3-min3 RN160 <- c(R1,R2,R3) tabeN160 <- data.frame(sd = c(p11, p12, p13), max = c(max1, max2, max3), min = c(min1, min2, min3), r = c(R1, R2, R3)) tabeN160
## sd max min r ## 1 0.01401841 0.2729419 0.2126402 0.0603017 ## 2 0.13931988 0.9773929 0.5059789 0.4714139 ## 3 0.01885297 0.9773929 0.5059789 0.4714139
Сравним минимальные и максимальные величины, величину размаха, среднеквадратическое отклонение между оценками для выборок объема 10,40,160 для ЭЗР.
id <- c("метод моментов для n = 10", "метод максимального правдоподобия для n = 10", "метод порядковых статистик для n = 10", "метод моментов для n = 40", "метод максимального правдоподобия для n = 40", "метод порядковых статистик для n = 40", "метод моментов для n = 160", "метод максимального правдоподобия для n = 160", "метод порядковых статистик для n = 160") p <- c(pN10,pN40,pN160) max <- c(maxN10,maxN40,maxN160) min <- c(minN10,minN40,minN160) R <- c(RN10,RN40,RN160) tableEZR <- data.frame(N = id, sd = p, Max = max, Min = min, R = R) tableEZR
## N sd Max Min ## 1 метод моментов для n = 10 0.09676093 0.5775761 0.1094630 ## 2 метод максимального правдоподобия для n = 10 0.19709799 0.9706065 0.1422553 ## 3 метод порядковых статистик для n = 10 0.09920512 0.9706065 0.1422553 ## 4 метод моментов для n = 40 0.03572868 0.3120266 0.1688482 ## 5 метод максимального правдоподобия для n = 40 0.16309205 0.9209055 0.2512482 ## 6 метод порядковых статистик для n = 40 0.03149770 0.9209055 0.2512482 ## 7 метод моментов для n = 160 0.01401841 0.2729419 0.2126402 ## 8 метод максимального правдоподобия для n = 160 0.13931988 0.9773929 0.5059789 ## 9 метод порядковых статистик для n = 160 0.01885297 0.9773929 0.5059789 ## R ## 1 0.4681131 ## 2 0.8283513 ## 3 0.8283513 ## 4 0.1431784 ## 5 0.6696572 ## 6 0.6696572 ## 7 0.0603017 ## 8 0.4714139 ## 9 0.4714139
Сравнить графически среднеквадратические отклонения трех оценок для значений n=10, n=40 и n=160 для ЭЗР.
plot ( RN10 , col = " red ") lines ( RN10 , col = " red ")

plot ( RN40 , col = " blue ") lines ( RN40 , col = " blue ")

plot ( RN160 , col = " green " ) lines ( RN160 , col = " green " )

Среднеквадратичное отклонение с увеличением n уменьшается.
