линал теория к экзамену

Вопрос 1. Матрицы, действия с матрицами (сложение матриц, умножение на число, умножение матриц, транспонирование).

1. Сложение матриц – это алгоритм вычисления новой матрицы С при помощи попарного суммирования соответствующих элементов матриц А и В.

2. Умножение матриц на число:

3. Умножение матриц:

4. Транспонирование матриц

Вопрос 2. Определители квадратных матриц порядка n. Определение по индукции через разложение по первой строке.

1. Определители квадратных матриц порядка n:

2. Определение по индукции через разложение по первой строке:

Вопрос 3. Минор, алгебраическое дополнение. Теорема о разложении определителя по элементам строки (столбца) (без доказательства).

1. Минор:

2. Алгебраическое дополнение:

3. Теорема о разложении определителя по элементам строки (столбца):

Вопрос 4. Свойства определителей. Перестановка строк, транспонирование, линейное свойство. Следствия из свойств. Определители треугольной матрицы, блочной матрицы (без доказательства).

1. Свойства определителей:

2. Перестановка строк, транспонирование – написаны выше.

3. Определители треугольной матрицы:

4. Определители блочной матрицы:

Вопрос 5. Следствие из теоремы о разложении определителя (фальшивое разложение) (без доказательства).

Вопрос 6. Обратная матрица. Теорема об обратной матрице (с доказательством).

Вопрос 7. Матричная запись систем линейных алгебраических уравнений. Правило Крамера решения системы линейных алгебраических уравнений (с доказательством).

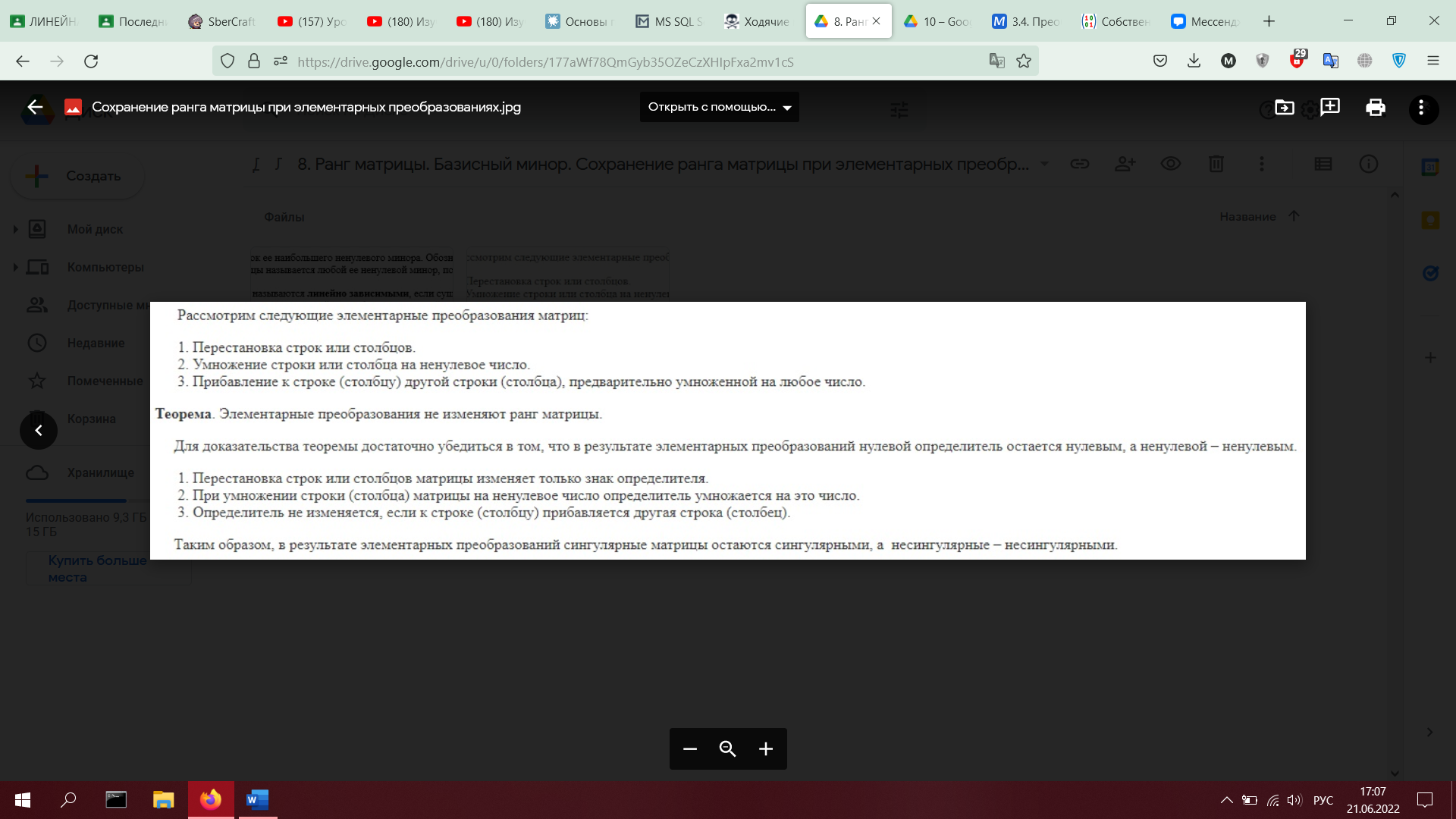
8. Ранг матрицы. Базисный минор. Сохранение ранга матрицы при элементарных преобразованиях (без доказательства).

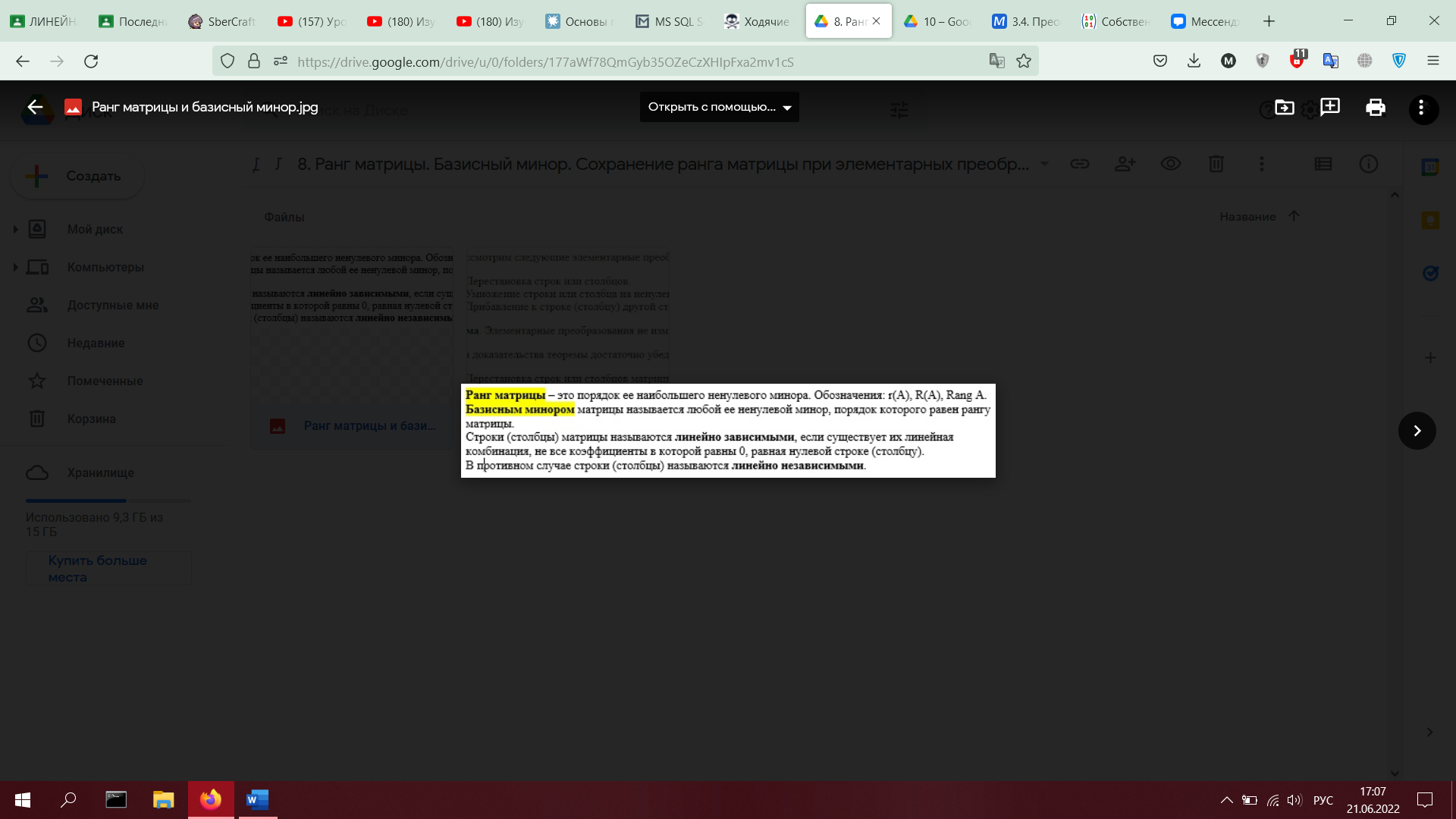
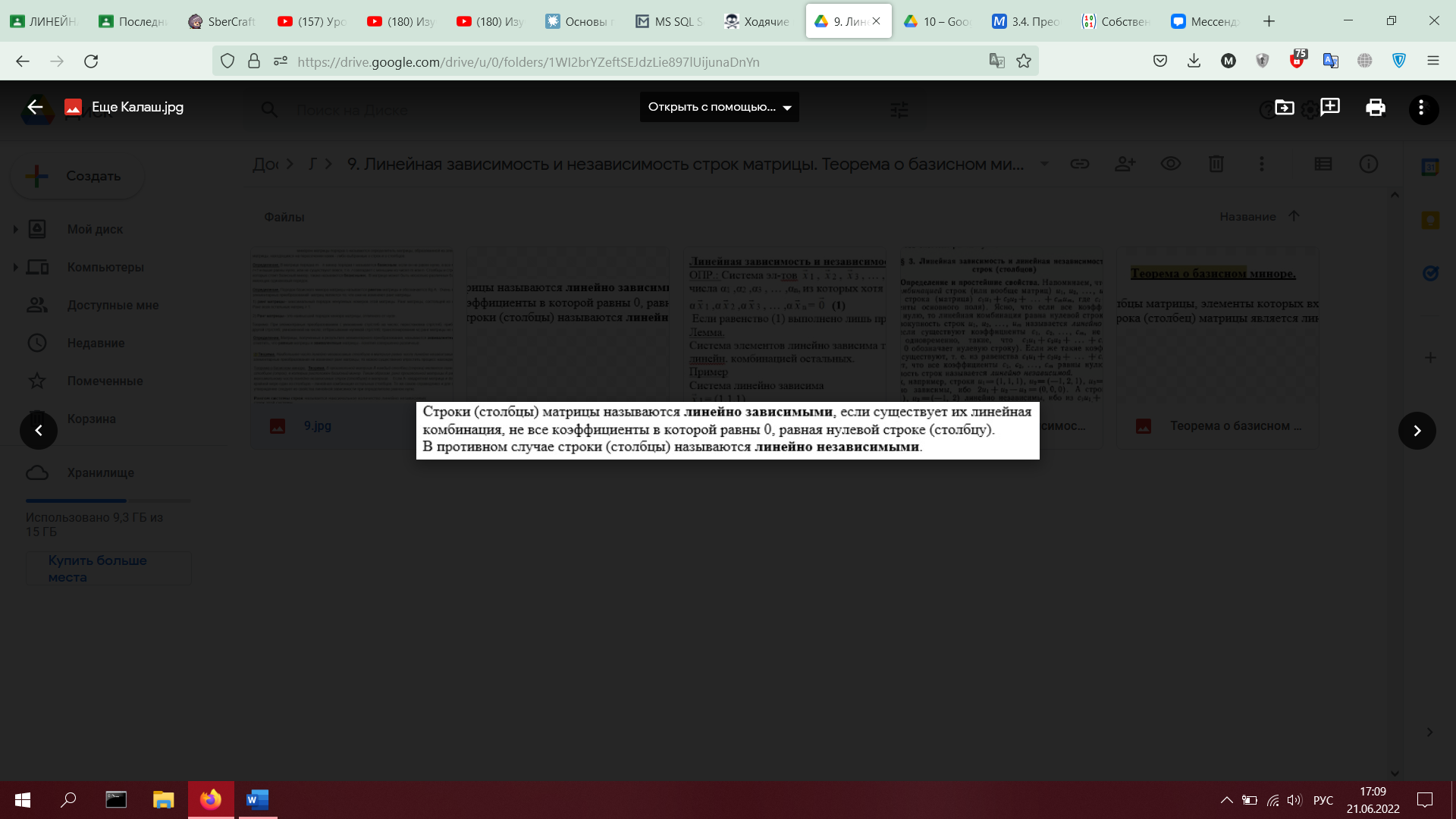
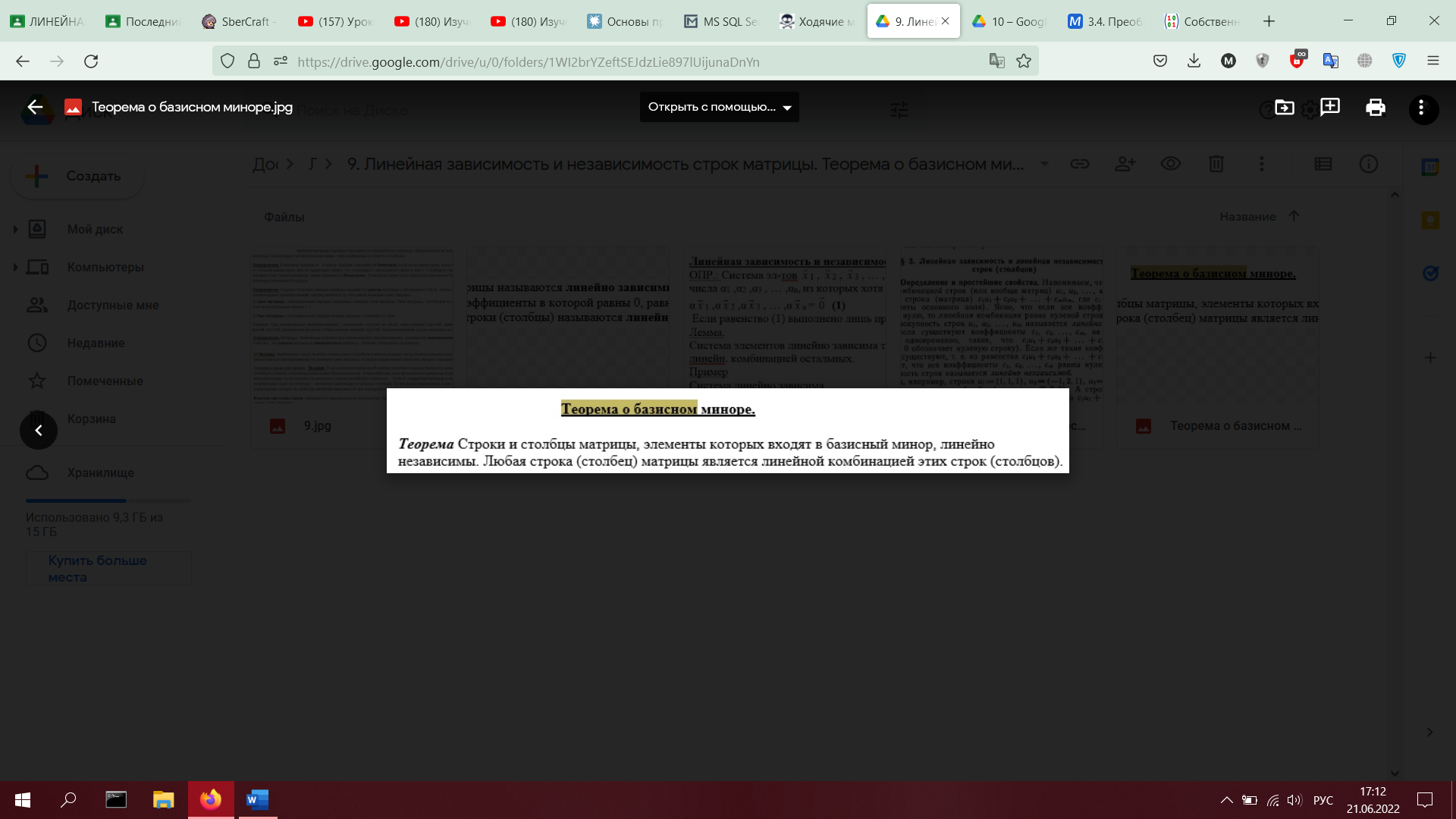
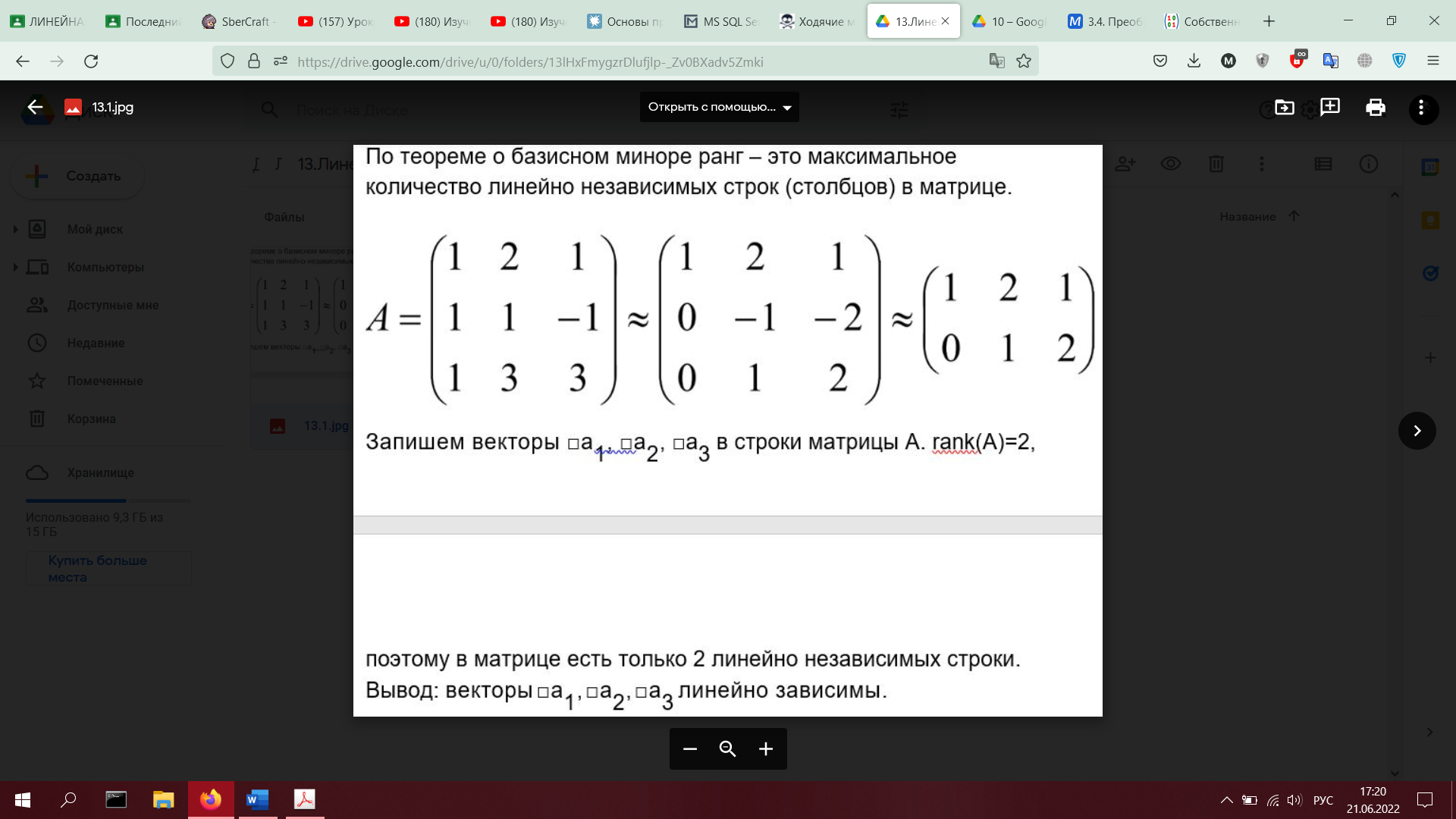
9. Линейная зависимость и независимость строк матрицы. Теорема о базисном миноре (без доказательства). Второе определение ранга матрицы: ранг – максимальное количество линейно независимых строк (столбцов) в матрице.

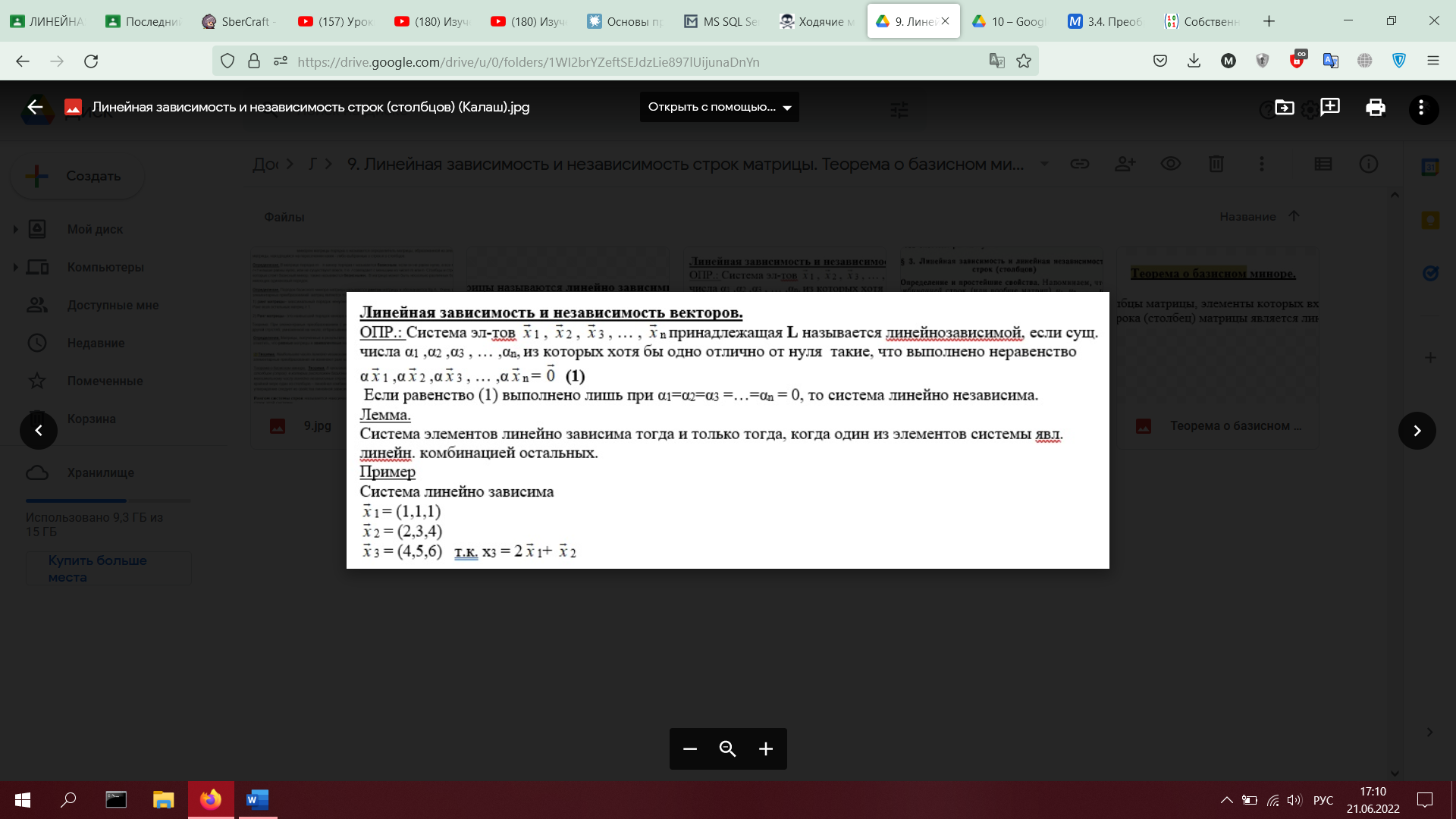
10. Теорема Кронекера – Капелли (с доказательством). Метод Гаусса на примере.

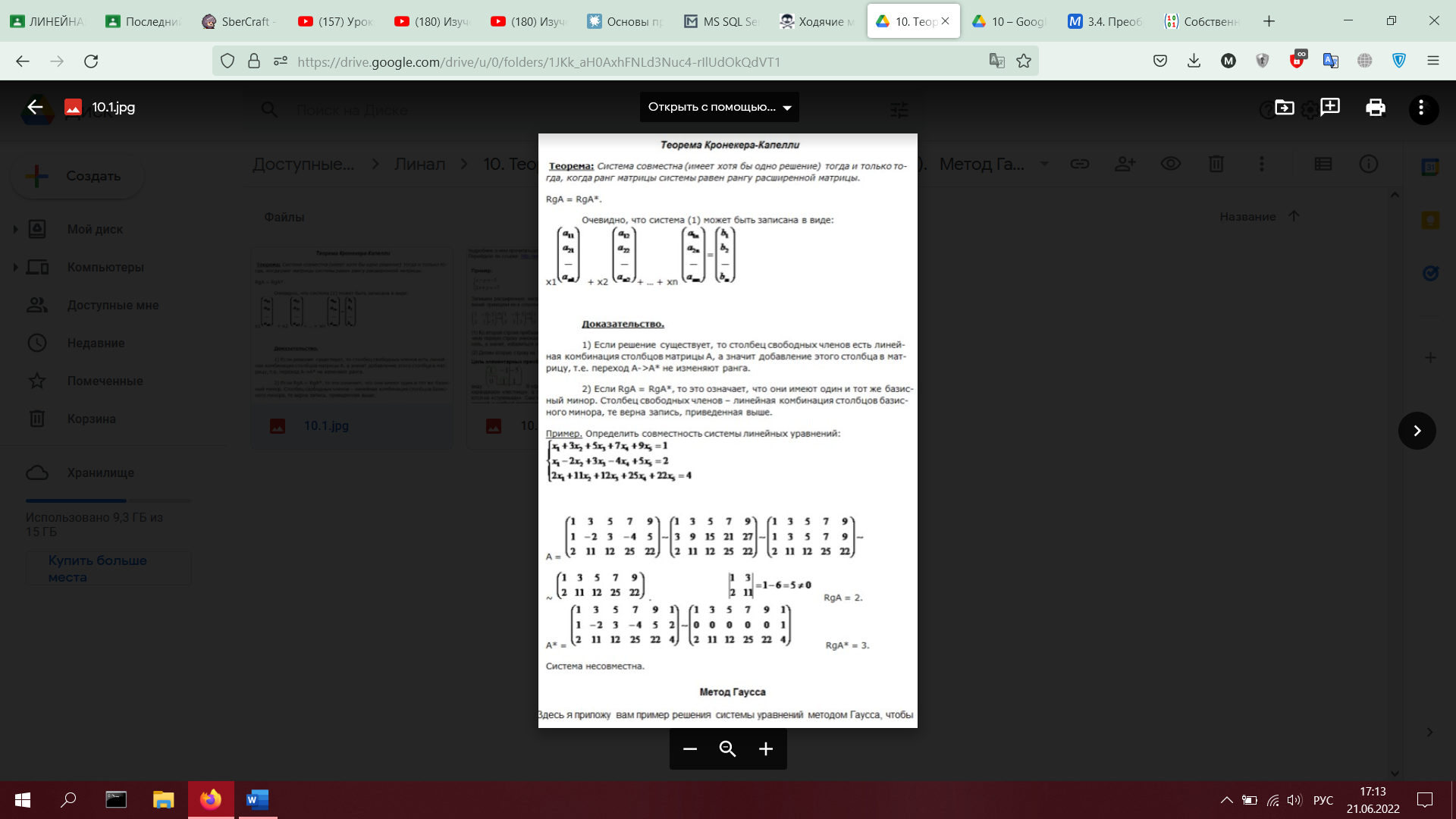
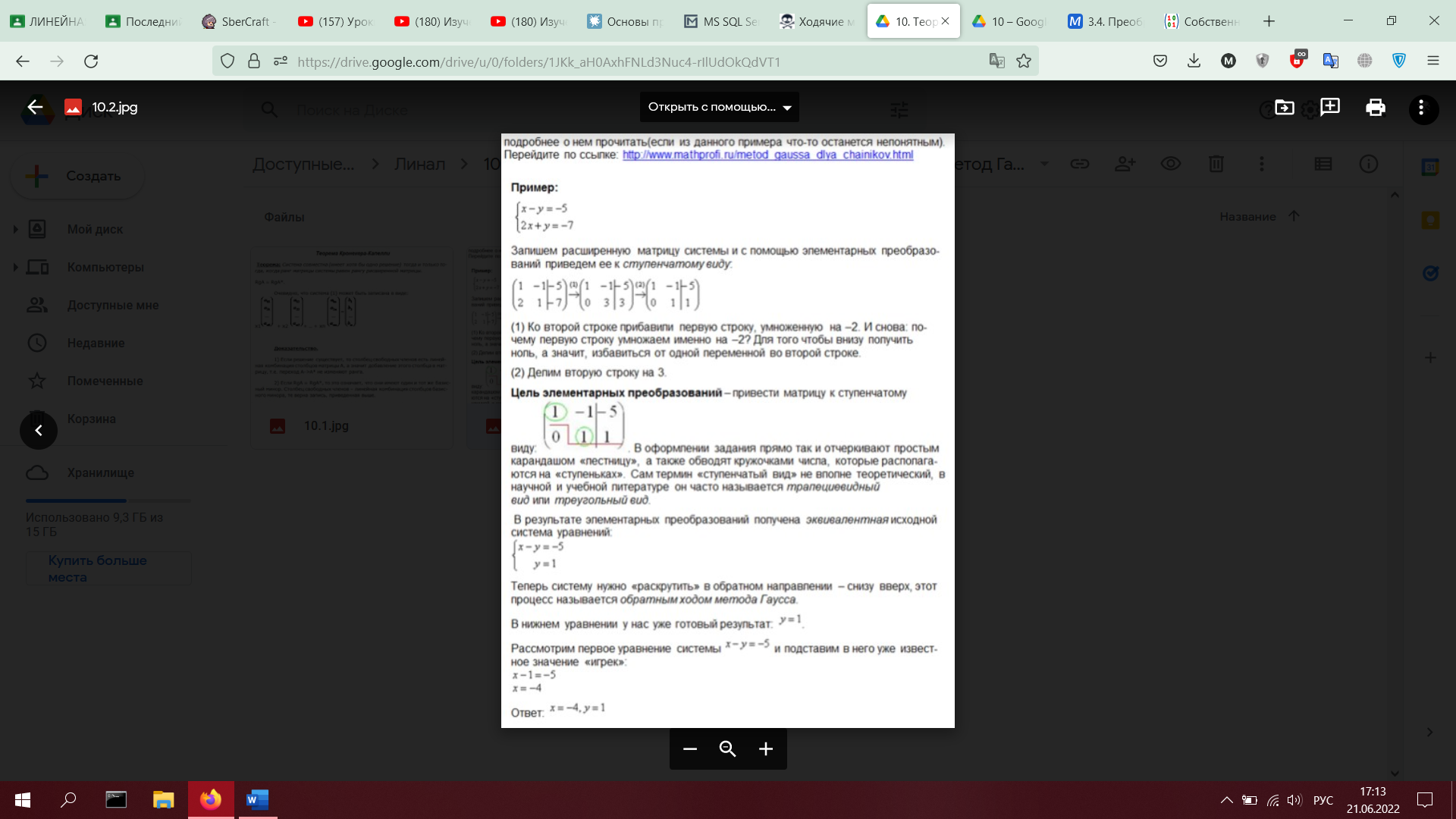
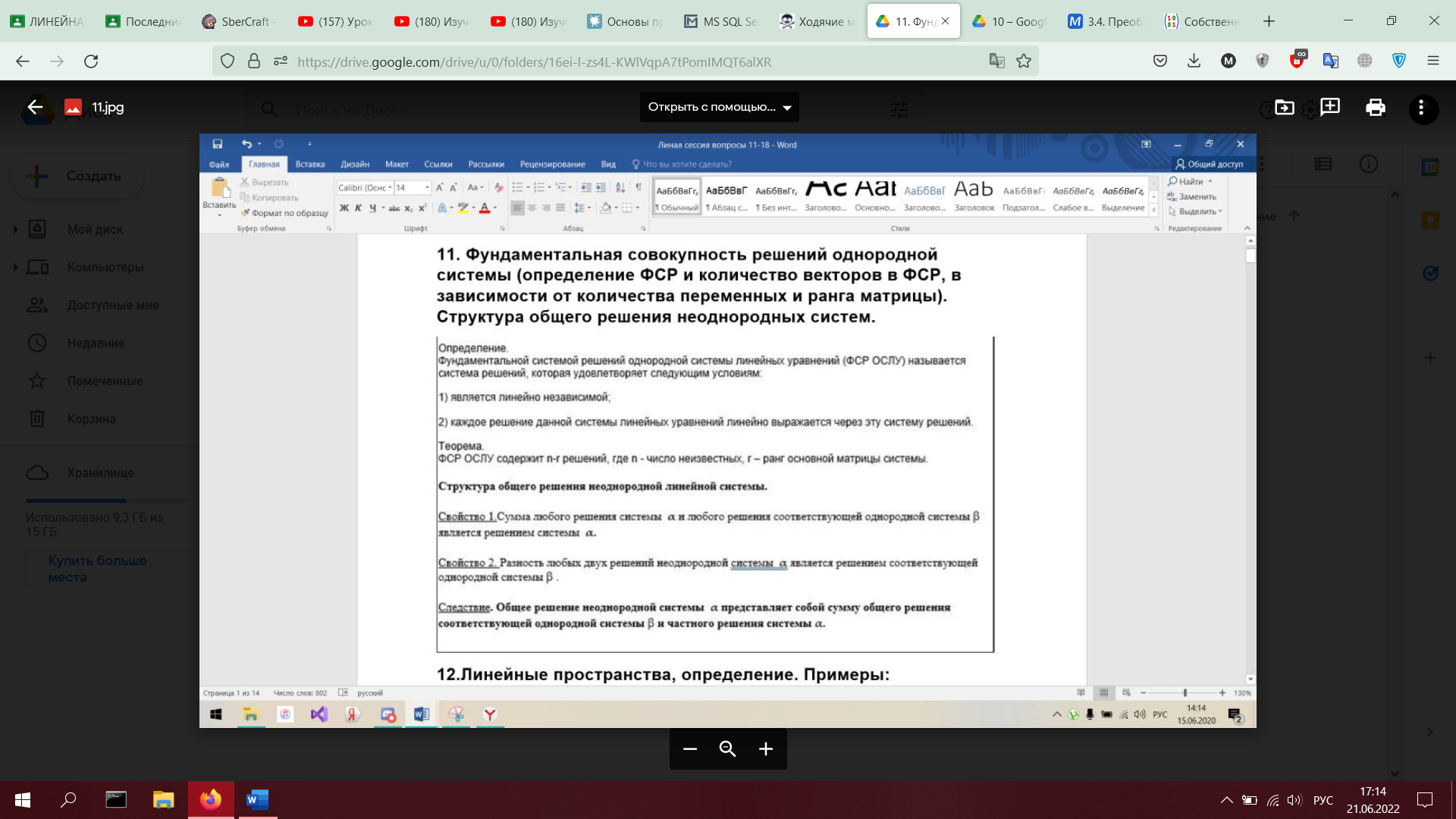
11. Фундаментальная совокупность решений однородной системы (определение ФСР и количество векторов в ФСР, в зависимости от количества переменных и ранга матрицы). Структура общего решения неоднородных систем.

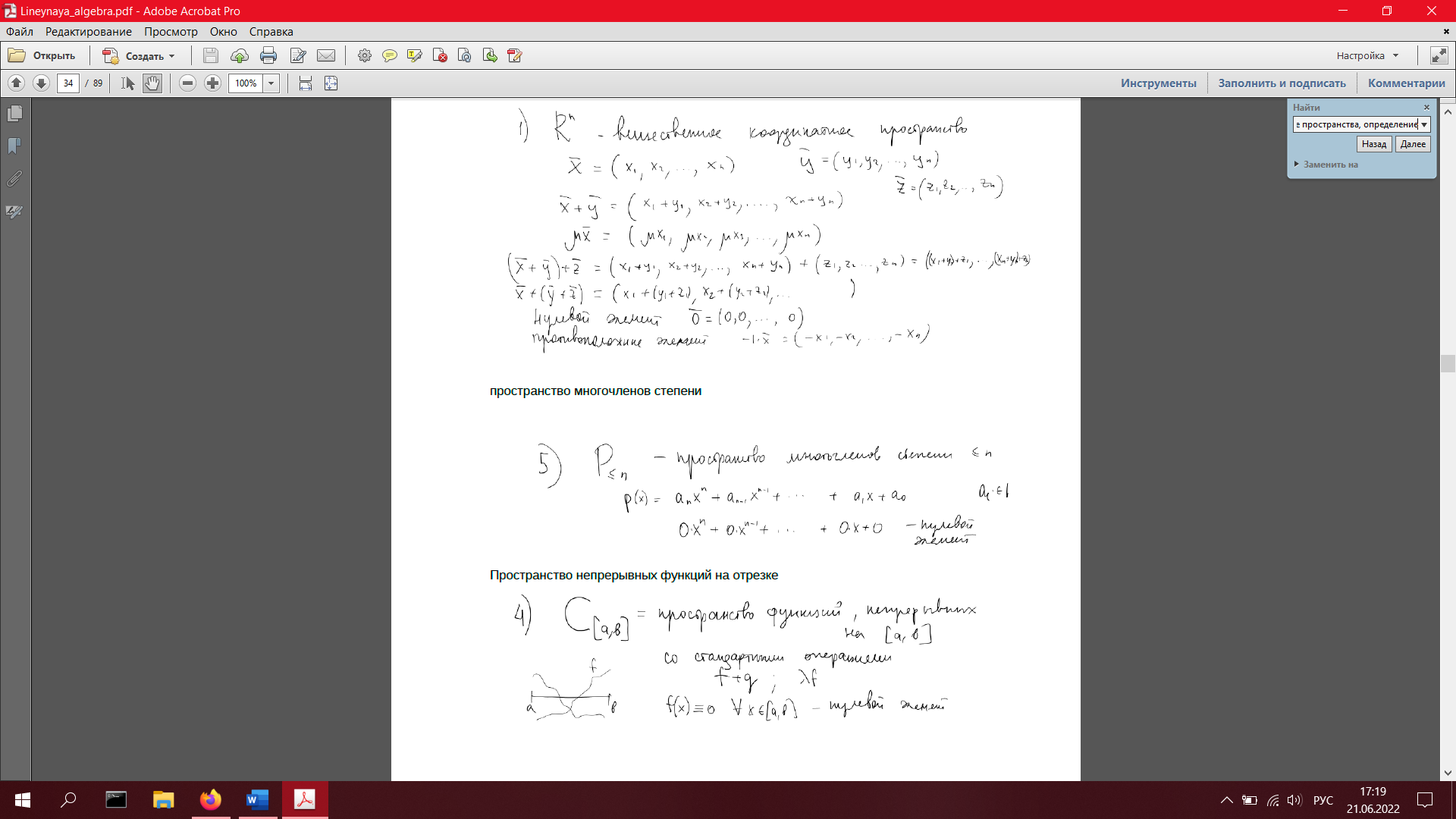
12. Линейные пространства, определение. Примеры: координатное вещественное пространство R^n, пространство многочленов степени ≤n, пространство непрерывных функций на отрезке [a,b].

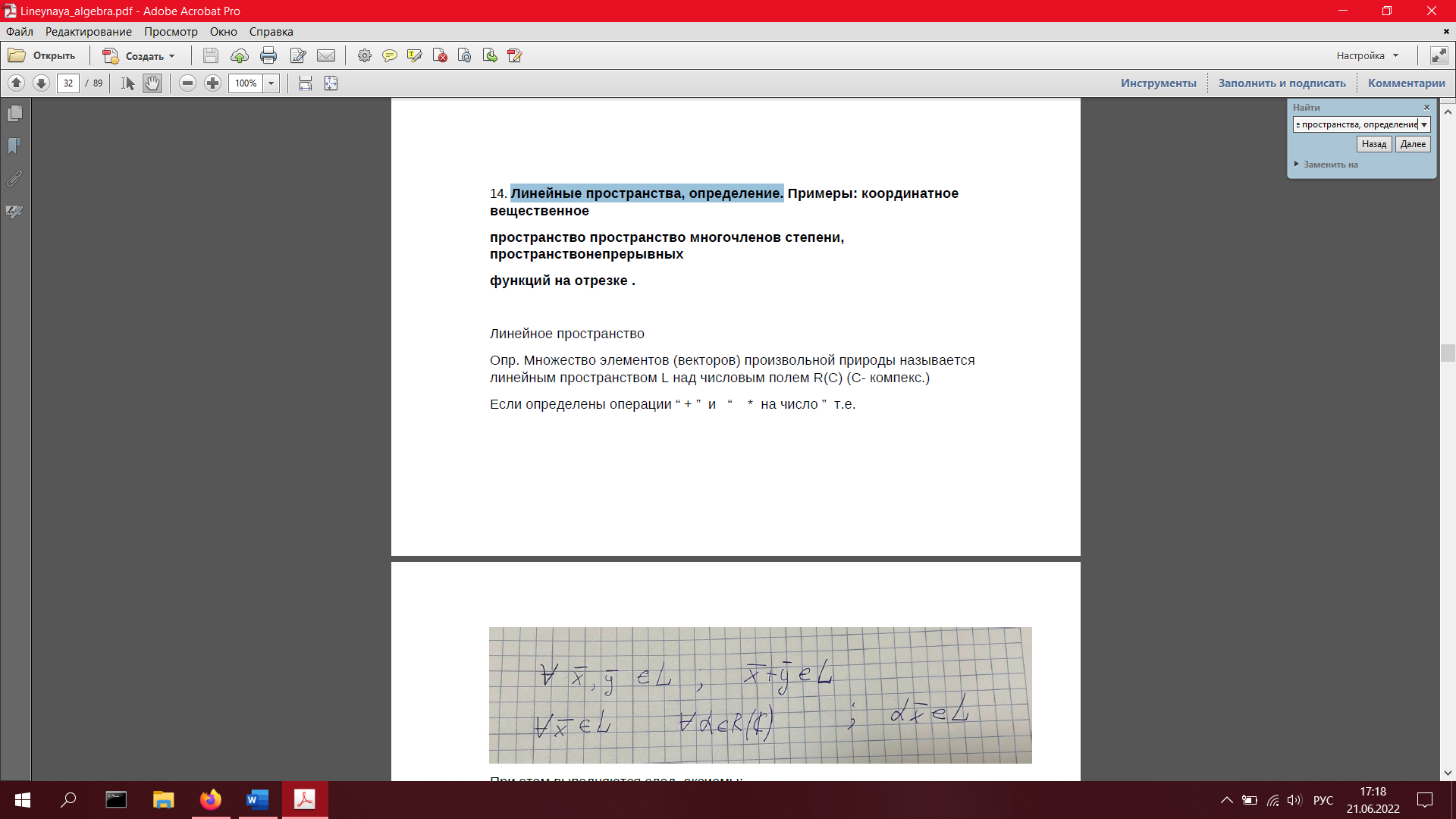
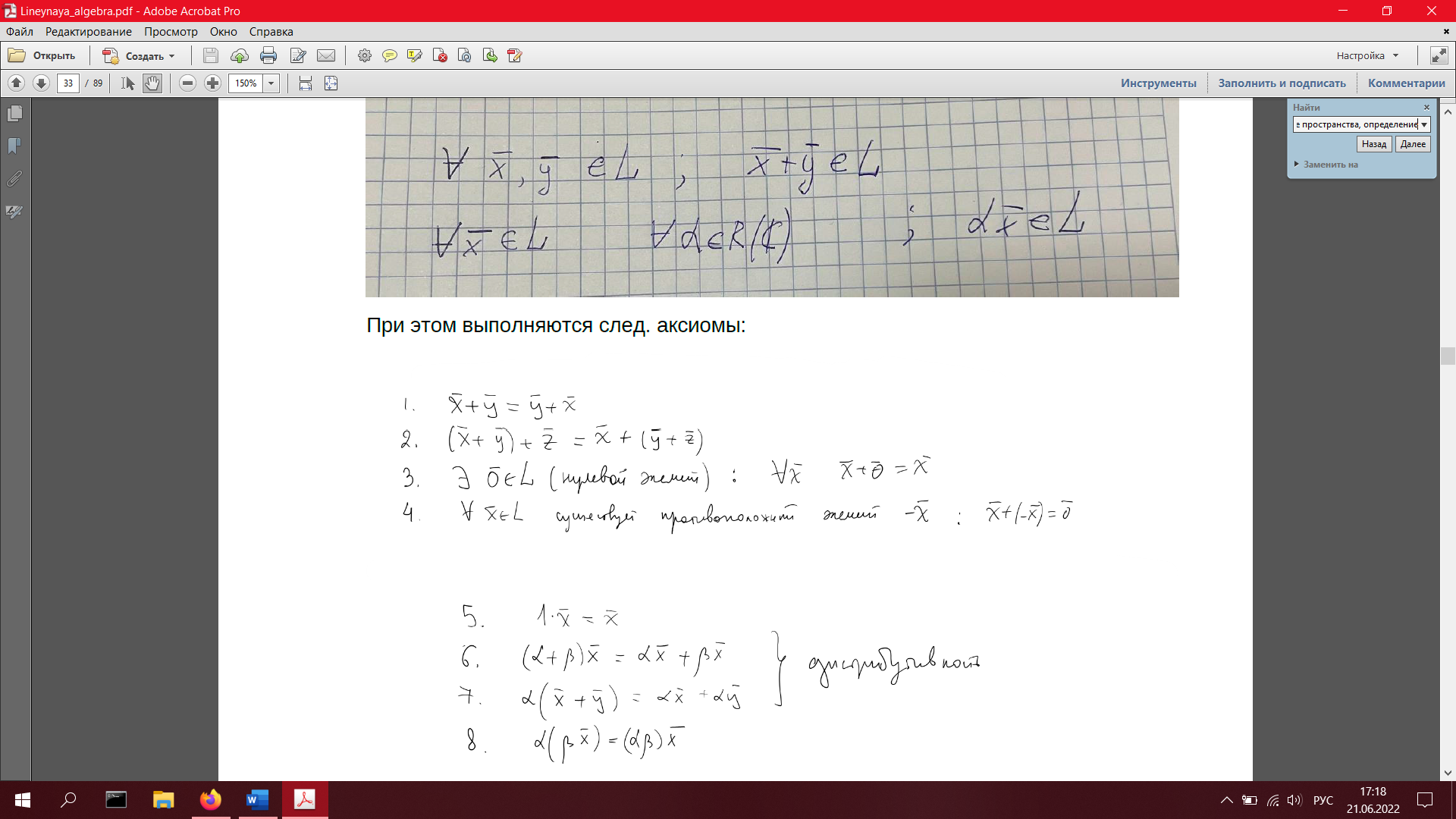
Координатное вещественное пространство

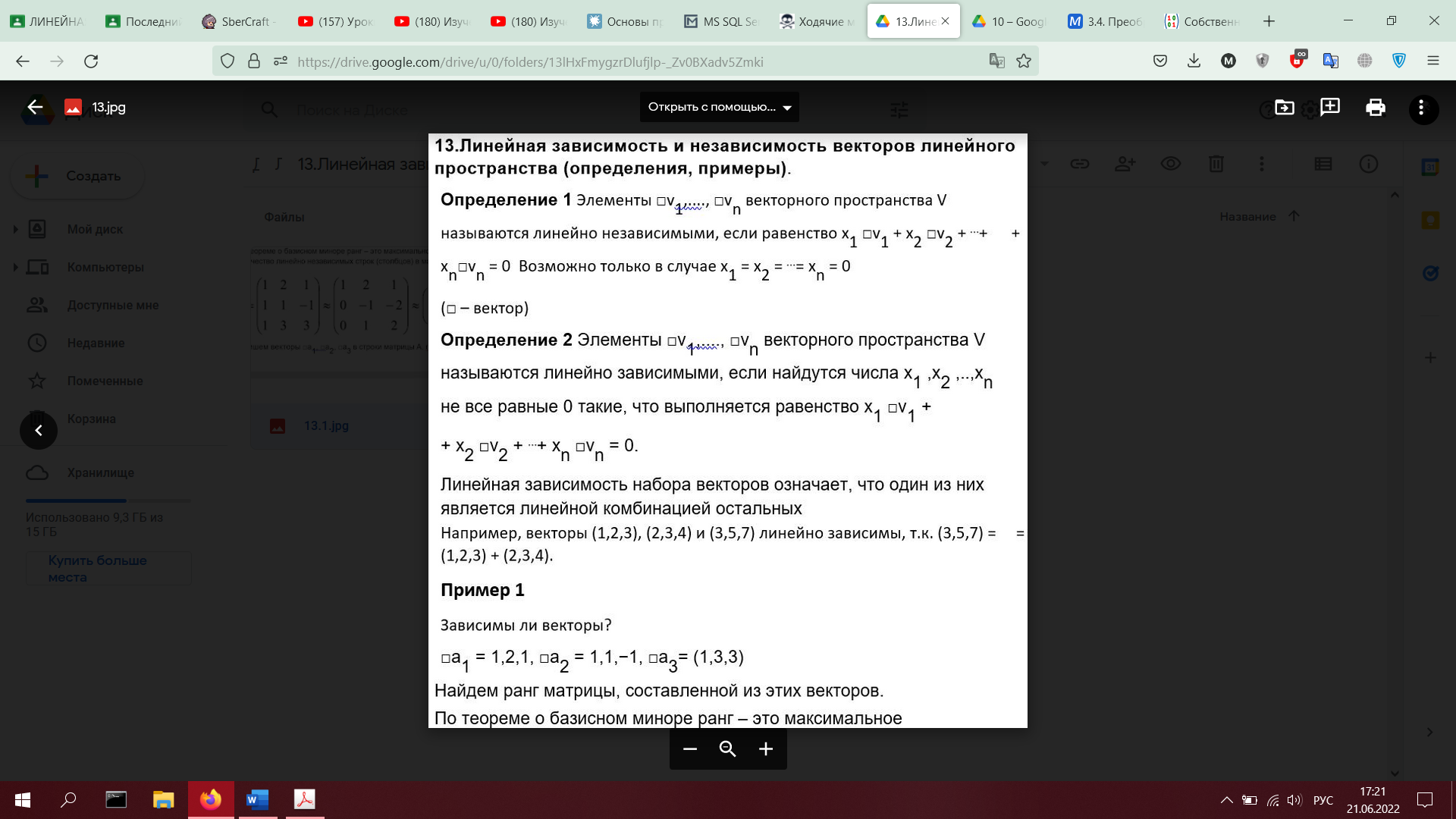
13. Линейная зависимость и независимость векторов линейного пространства (определения, примеры).

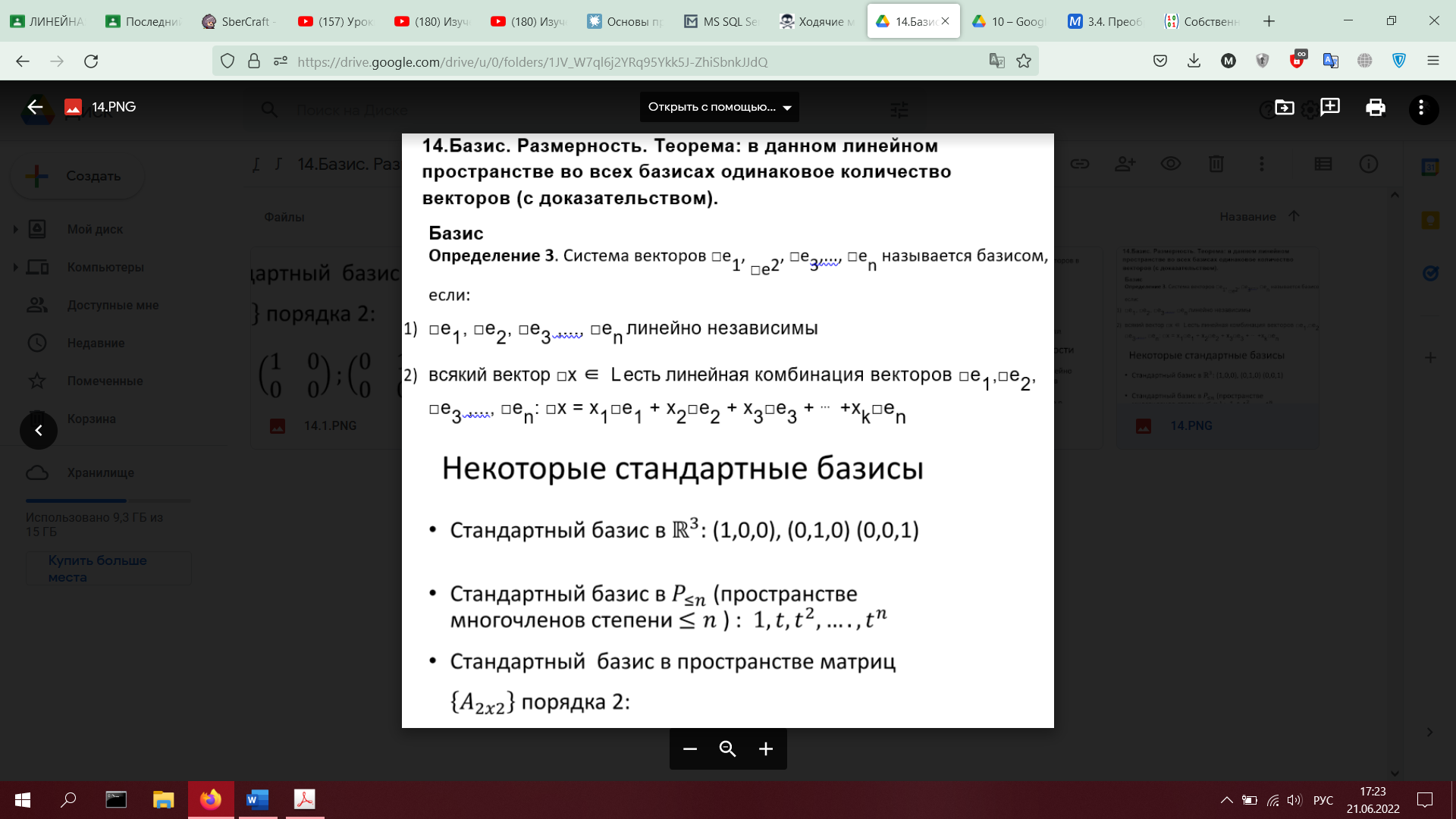
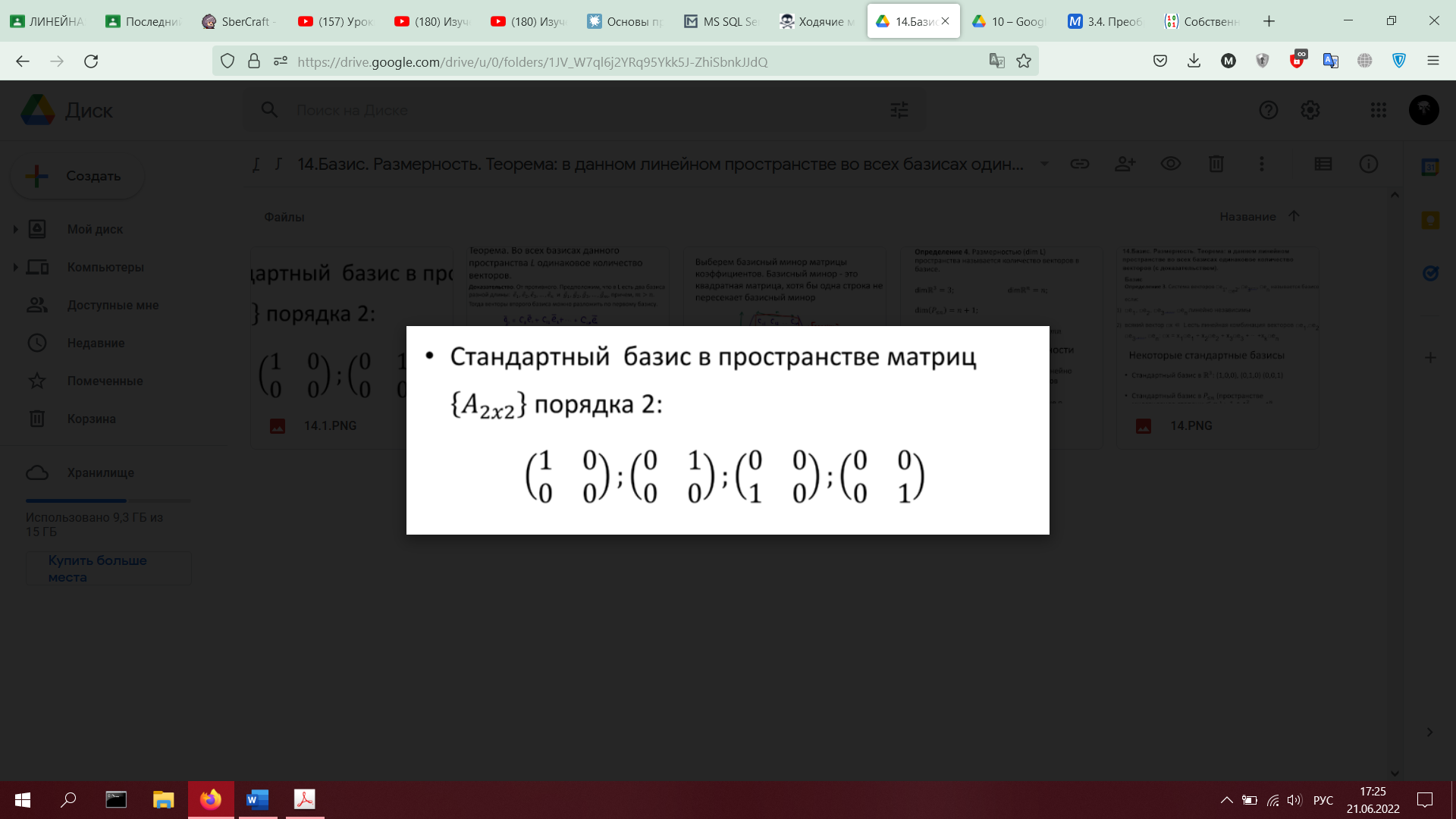
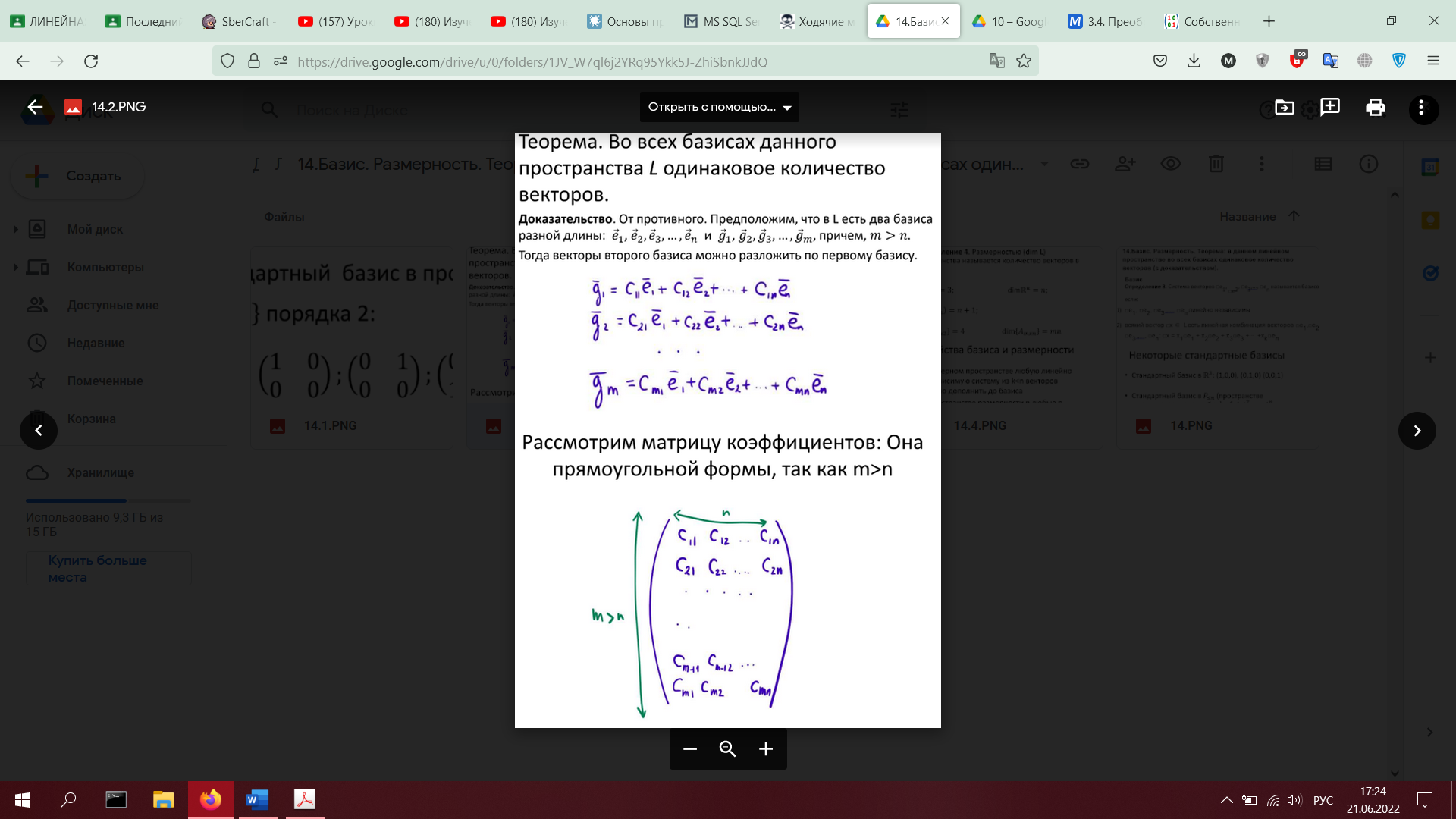
14. Базис. Размерность. Теорема: в данном линейном пространстве во всех базисах одинаковое количество векторов (с доказательством).

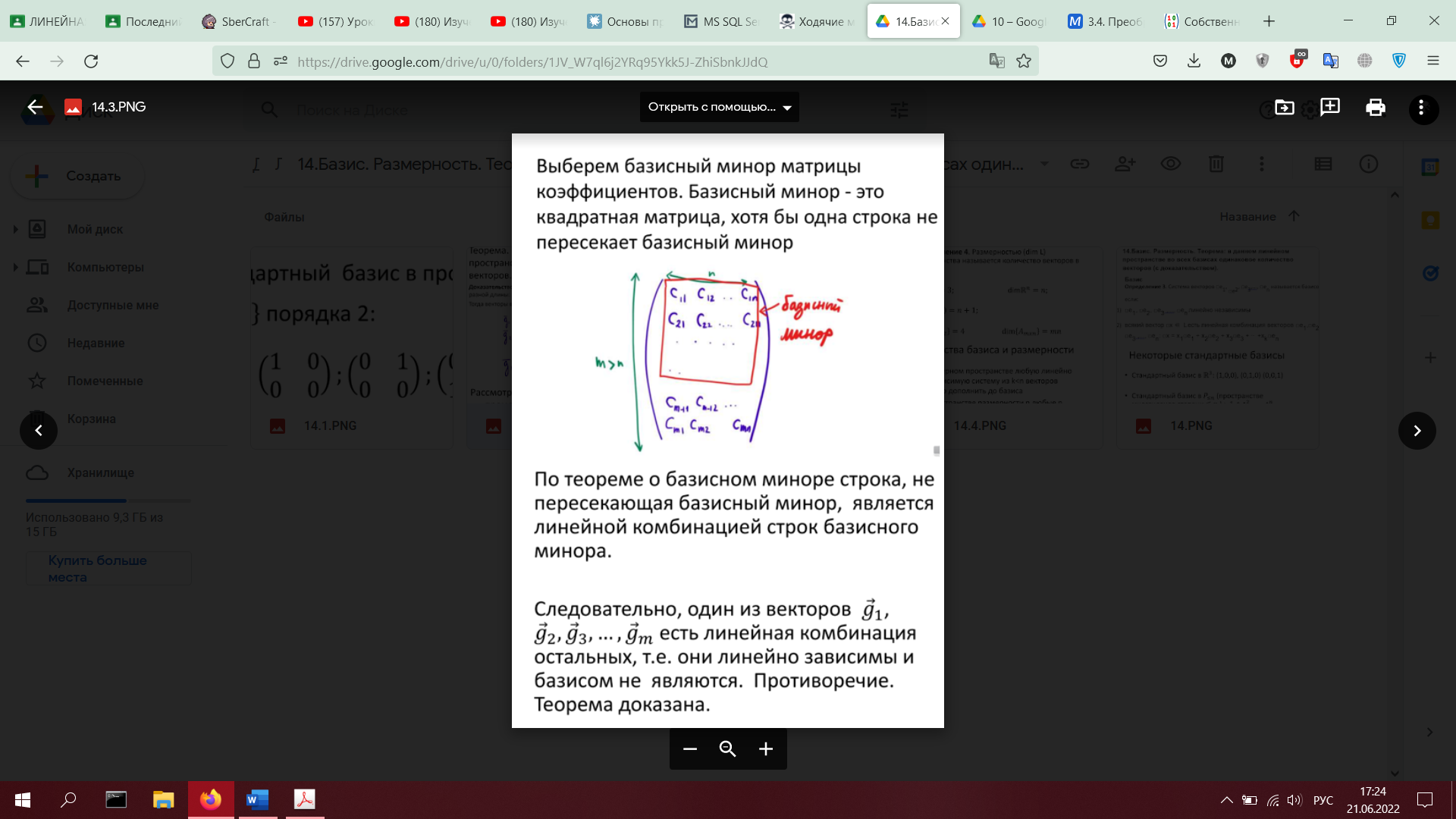
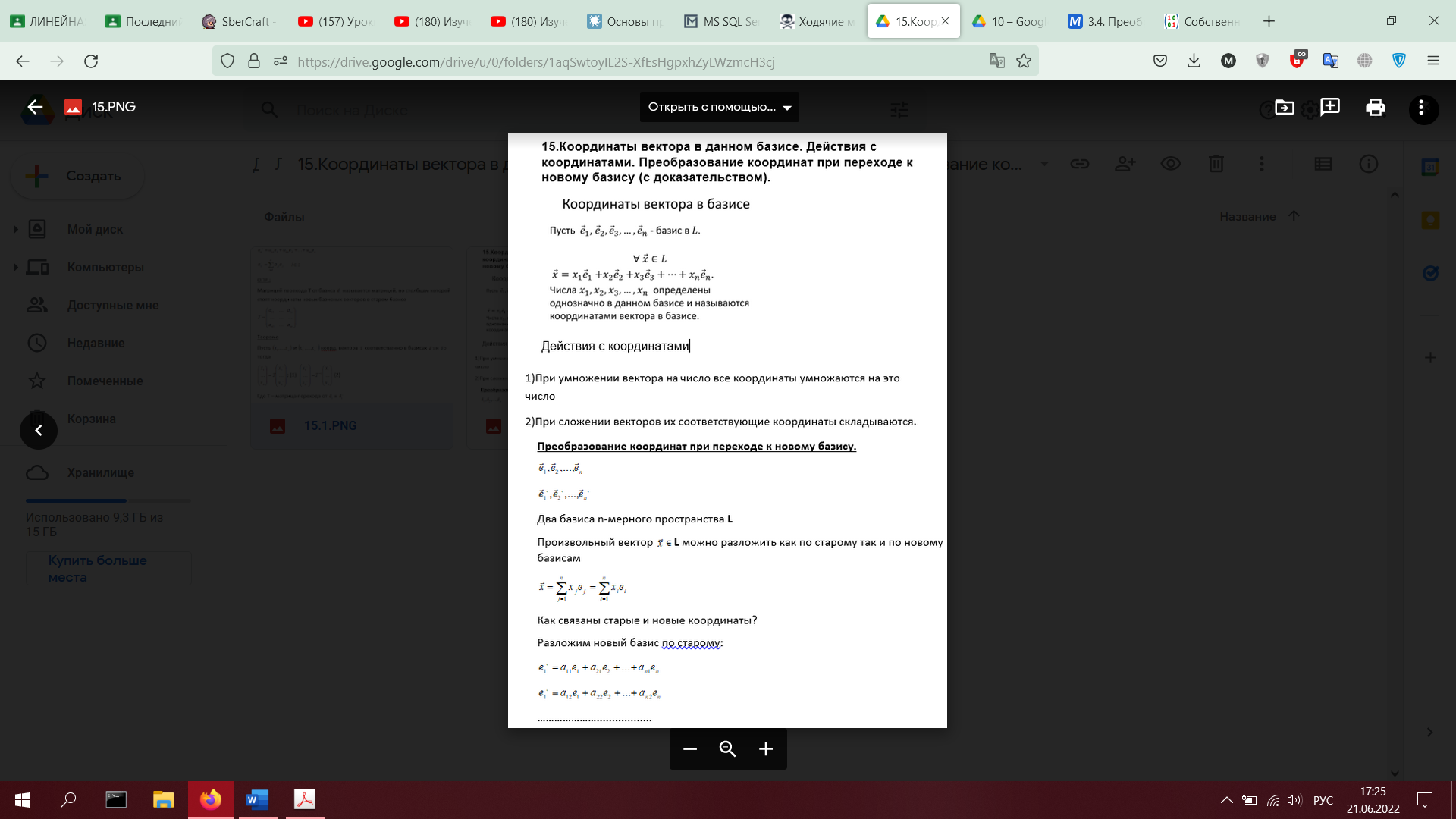
15. Координаты вектора в данном базисе. Действия с координатами. Преобразование координат при переходе к новому базису (с доказательством).

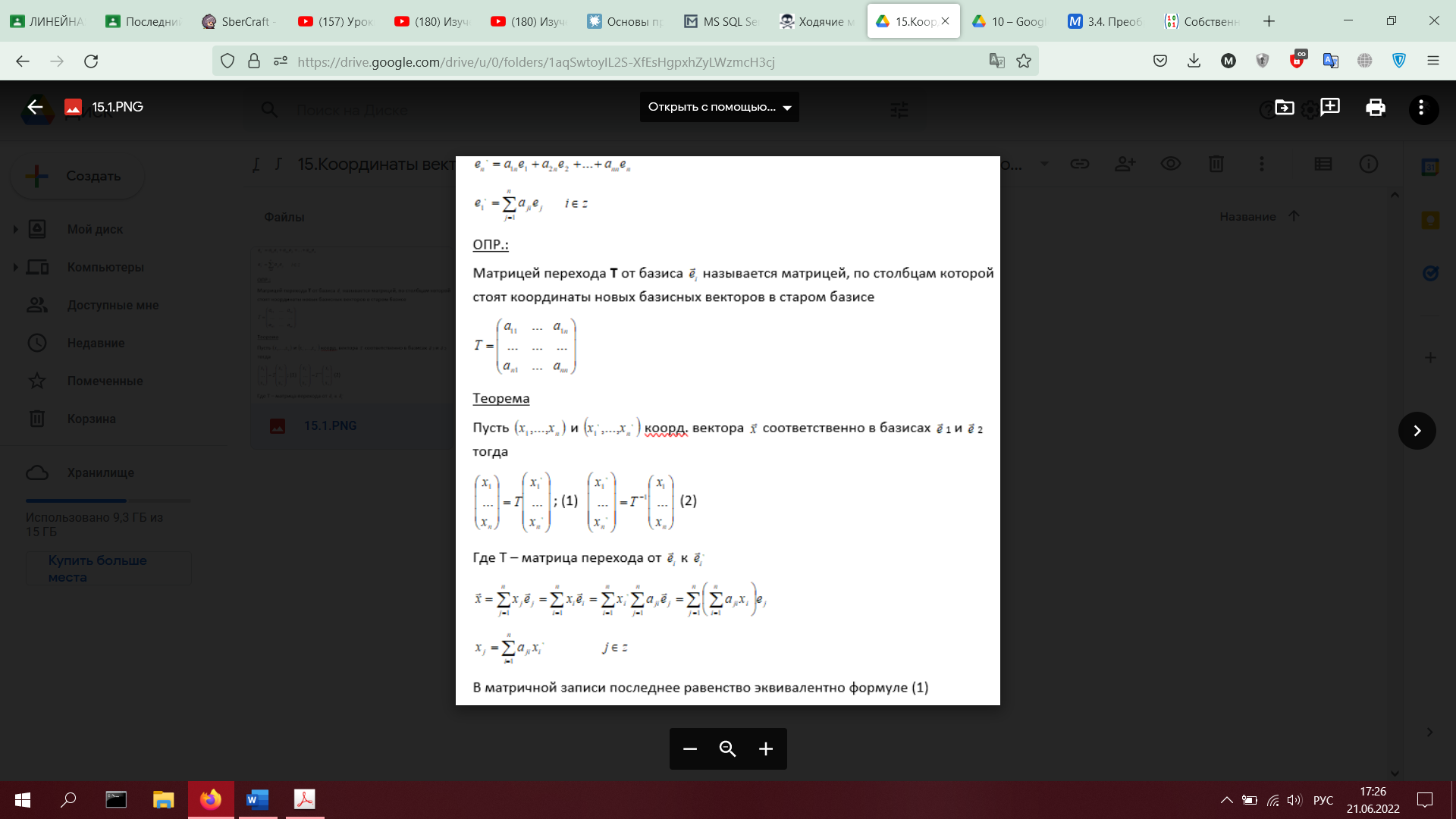
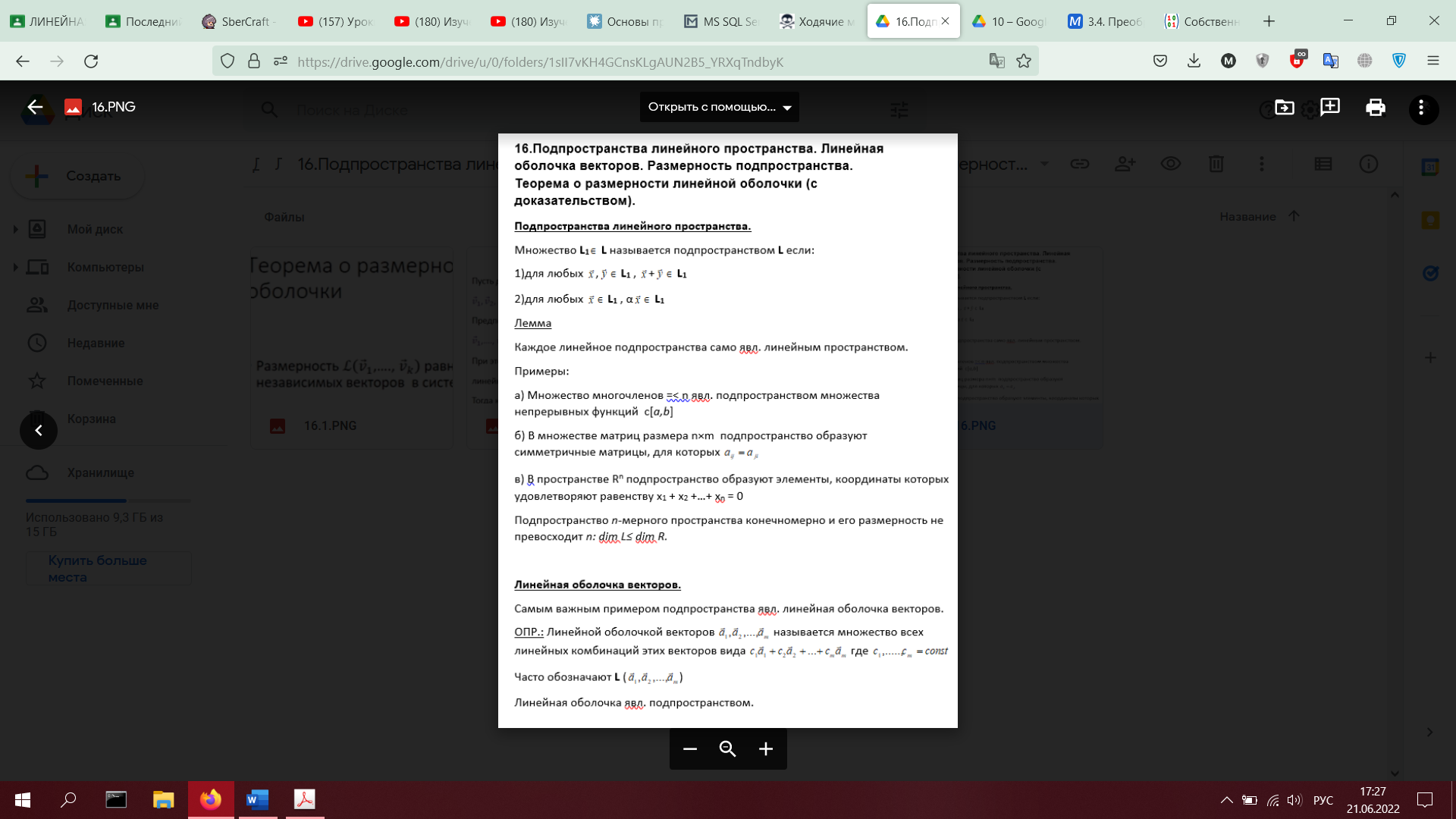
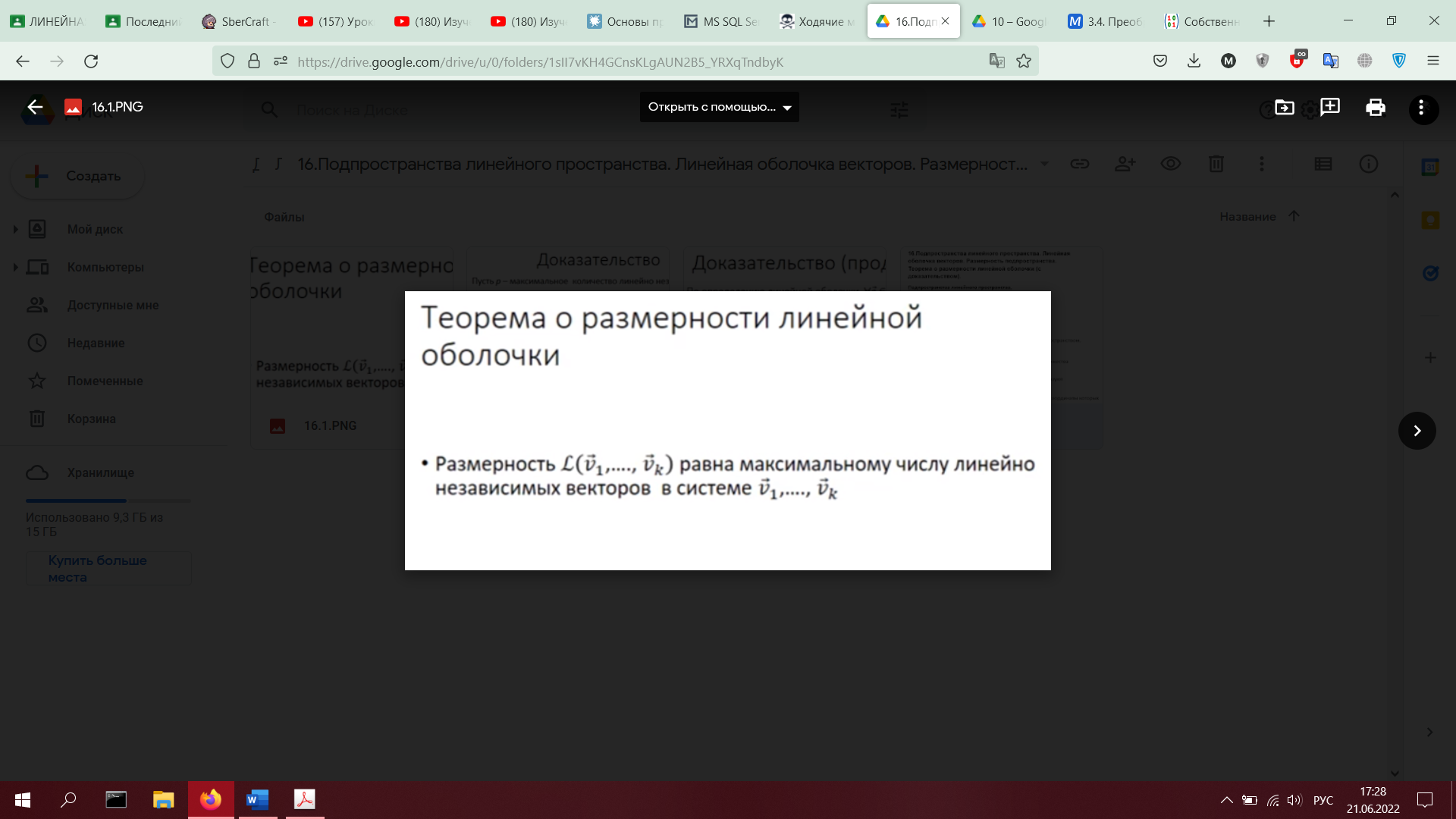
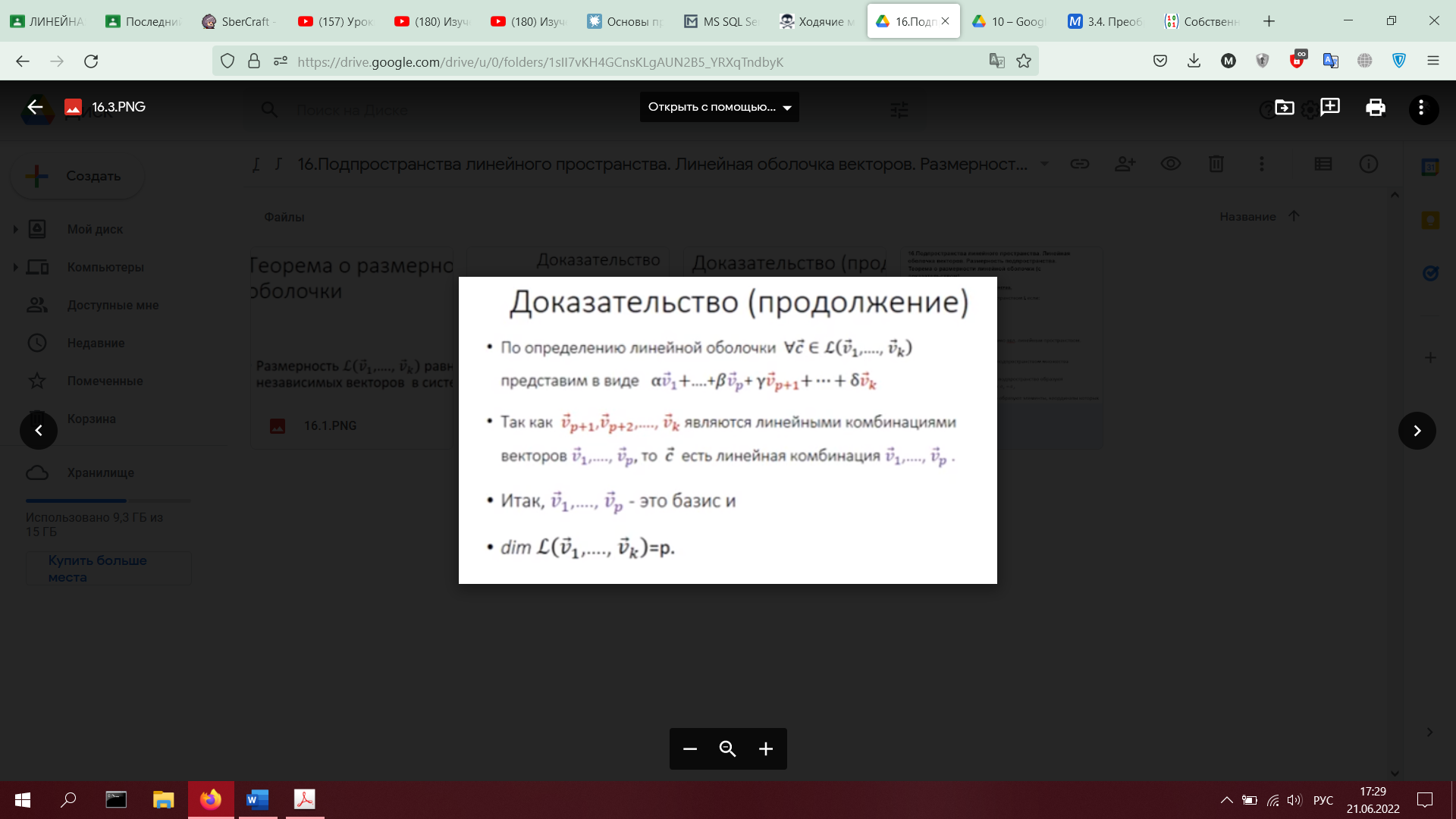
16. Подпространства линейного пространства. Линейная оболочка векторов. Размерность

подпространства. Теорема о размерности линейной оболочки (с доказательством).

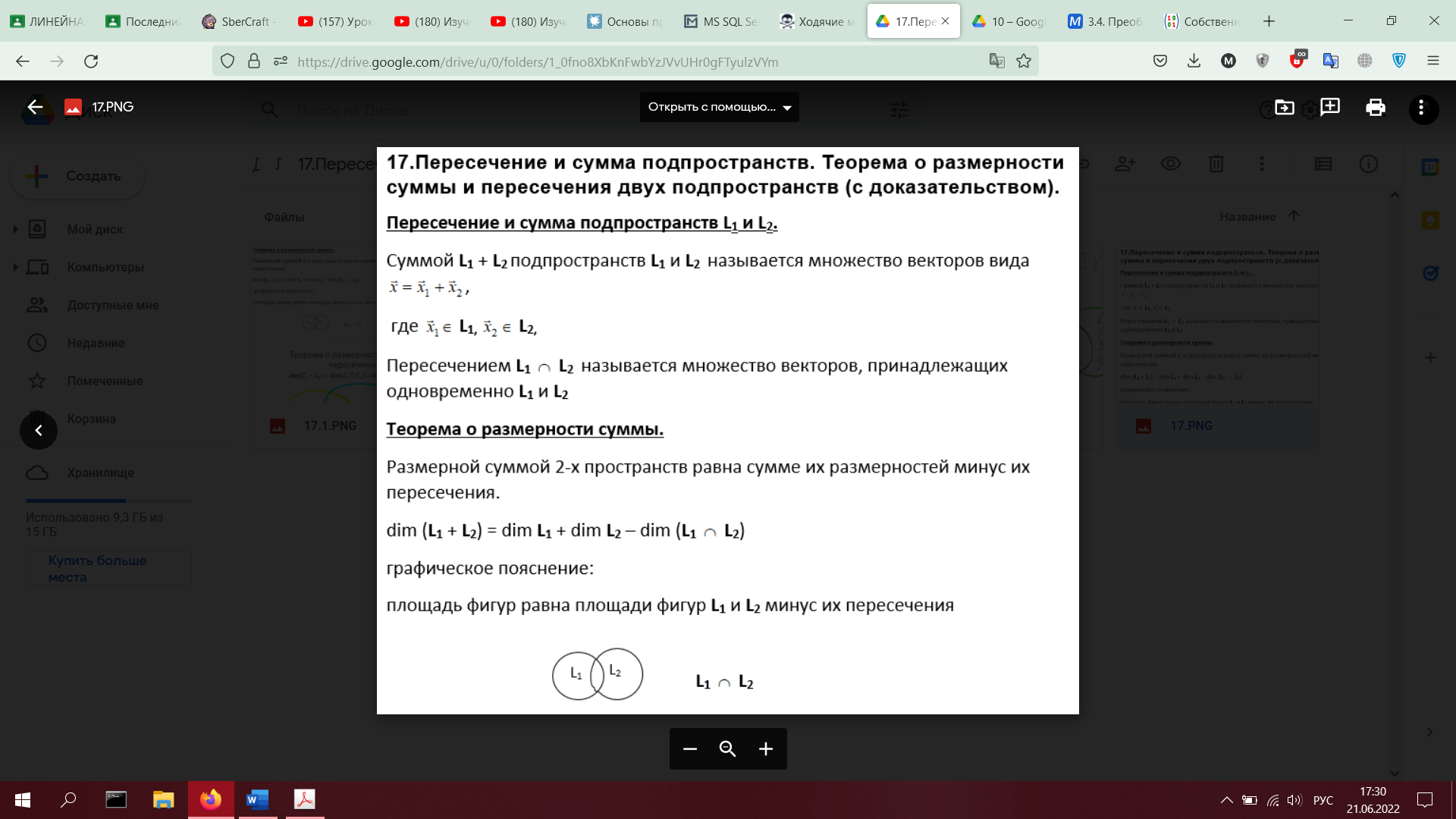
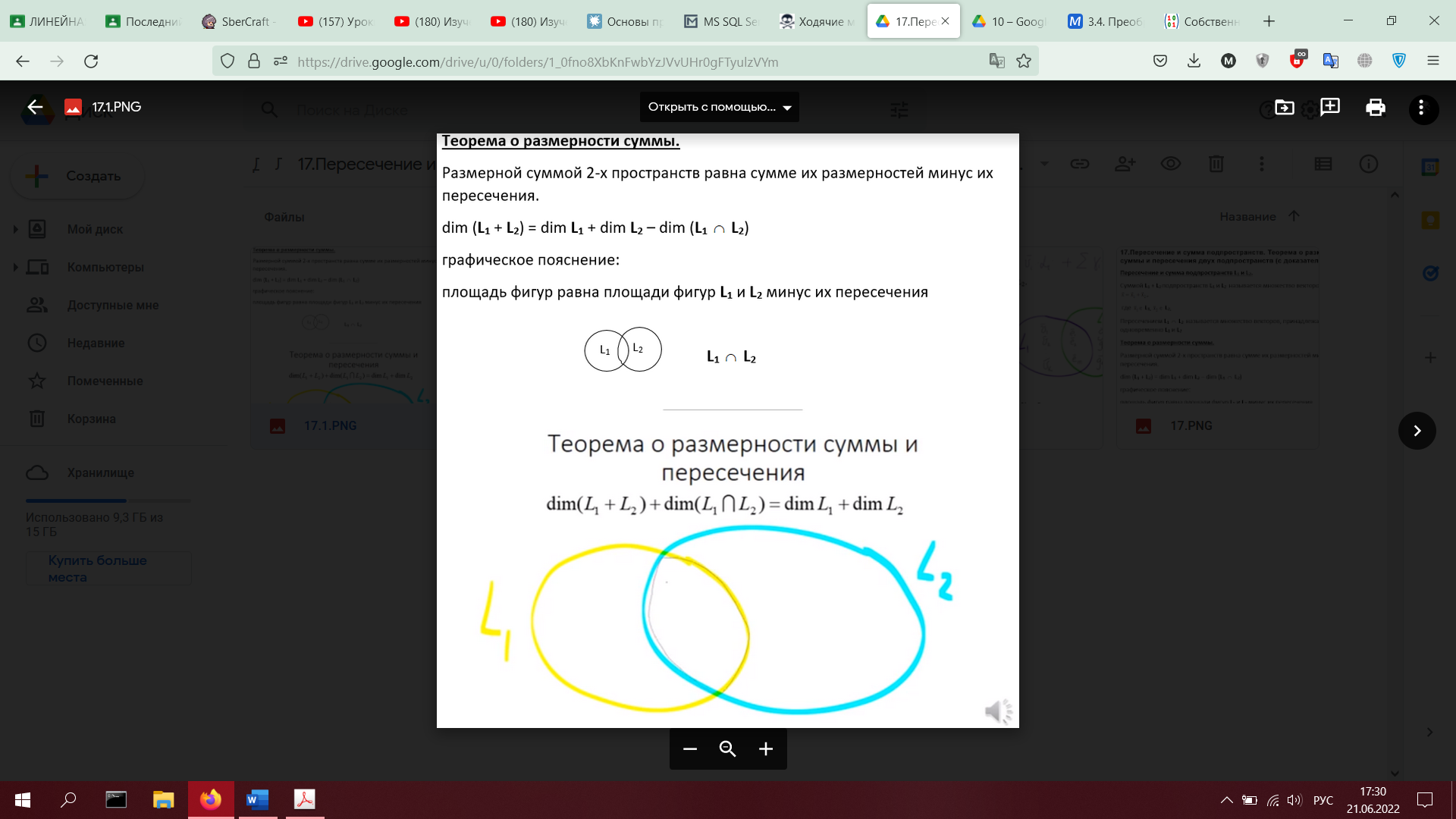
17. Пересечение и сумма подпространств. Теорема о размерности суммы и пересечения двух подпространств (с доказательством).

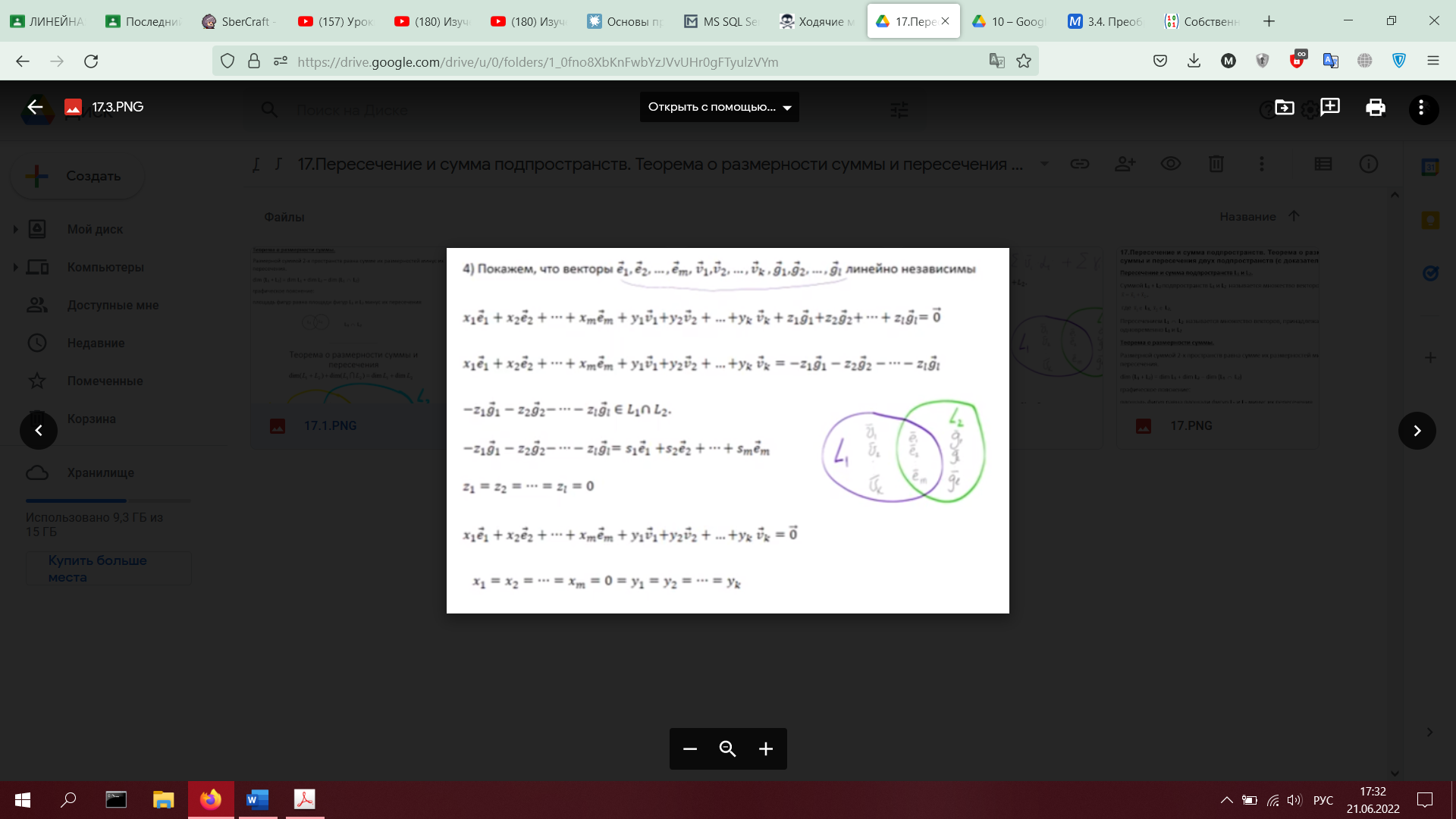
18. Прямая сумма подпространств. Определение.

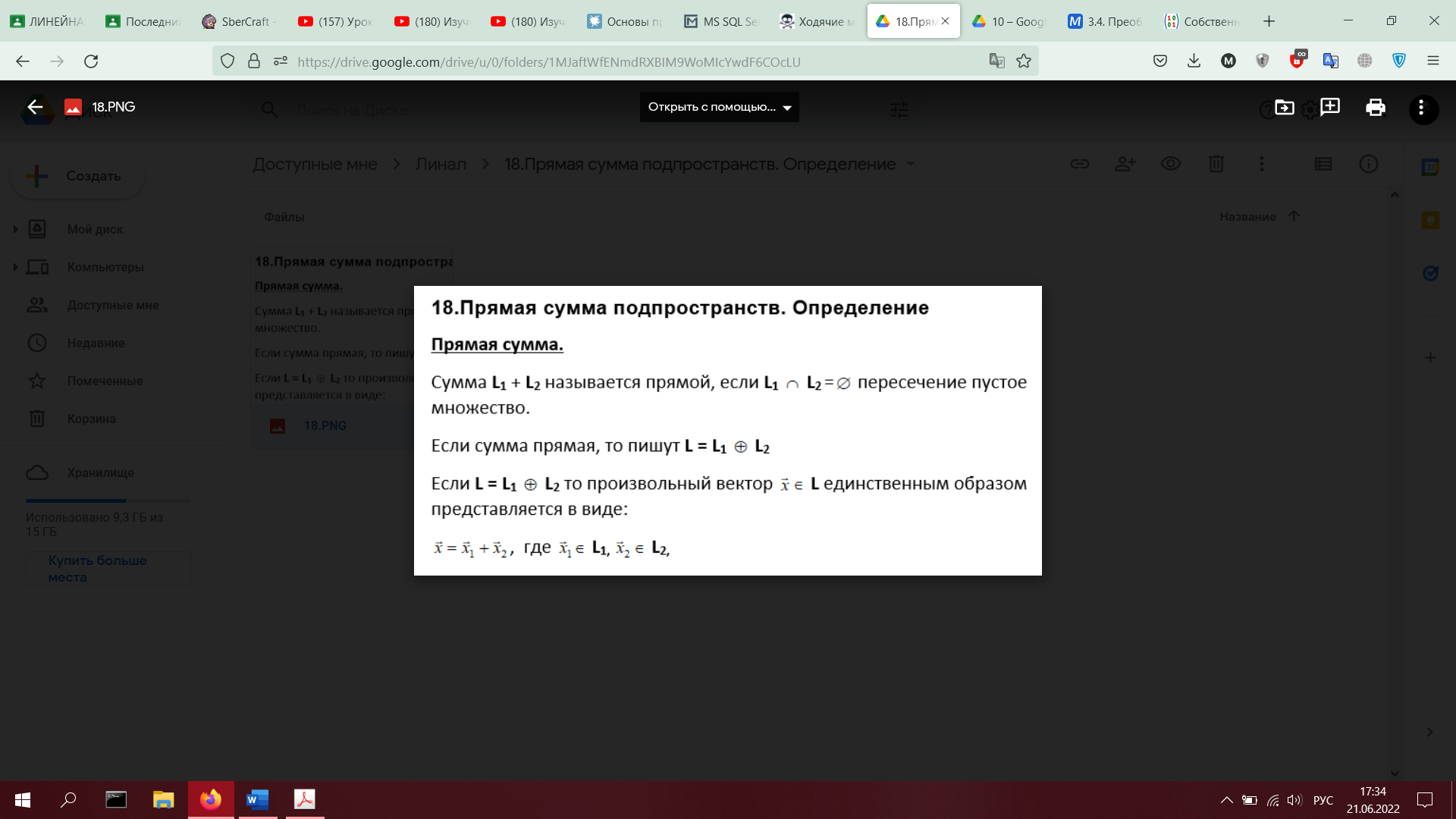
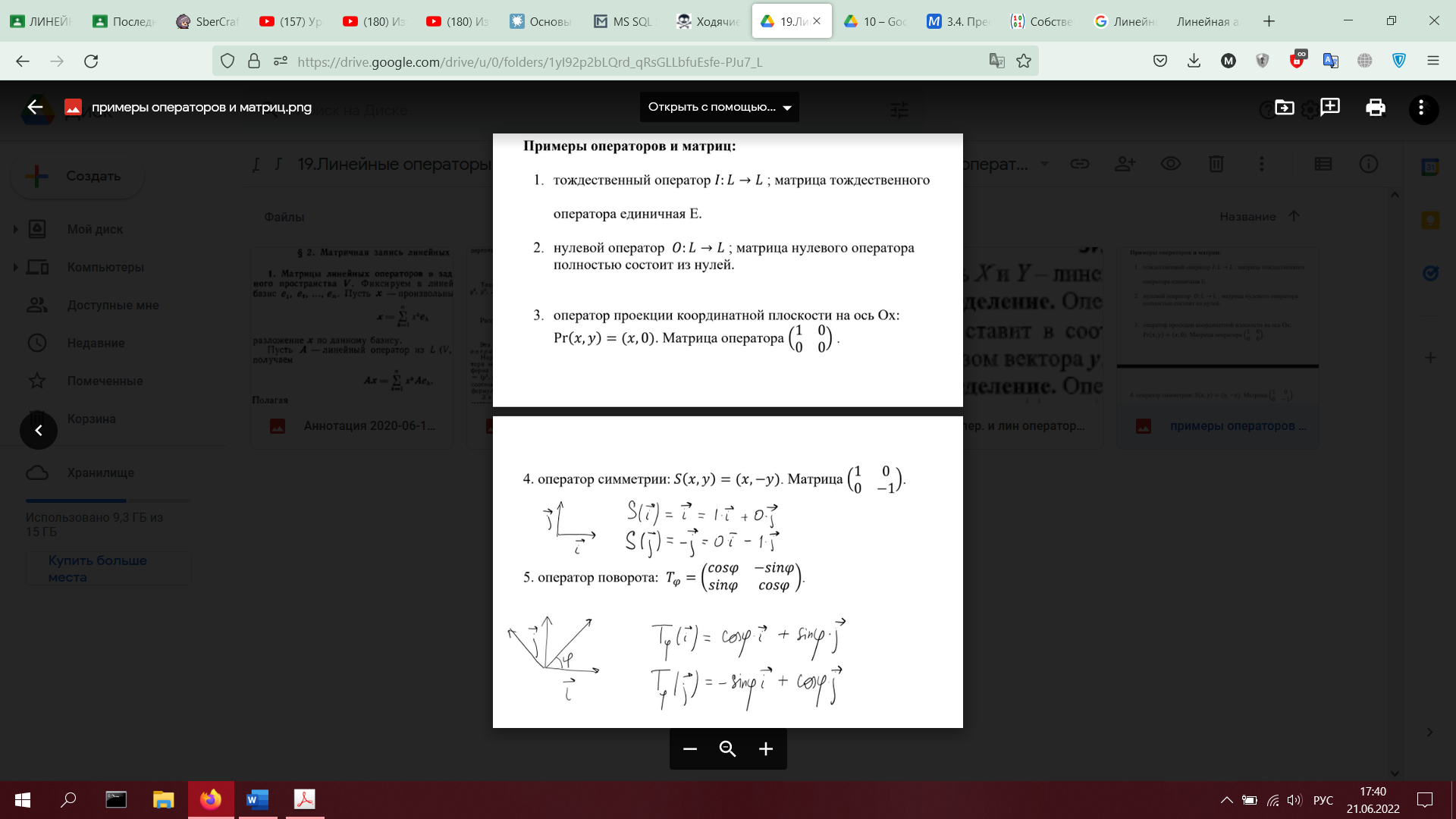
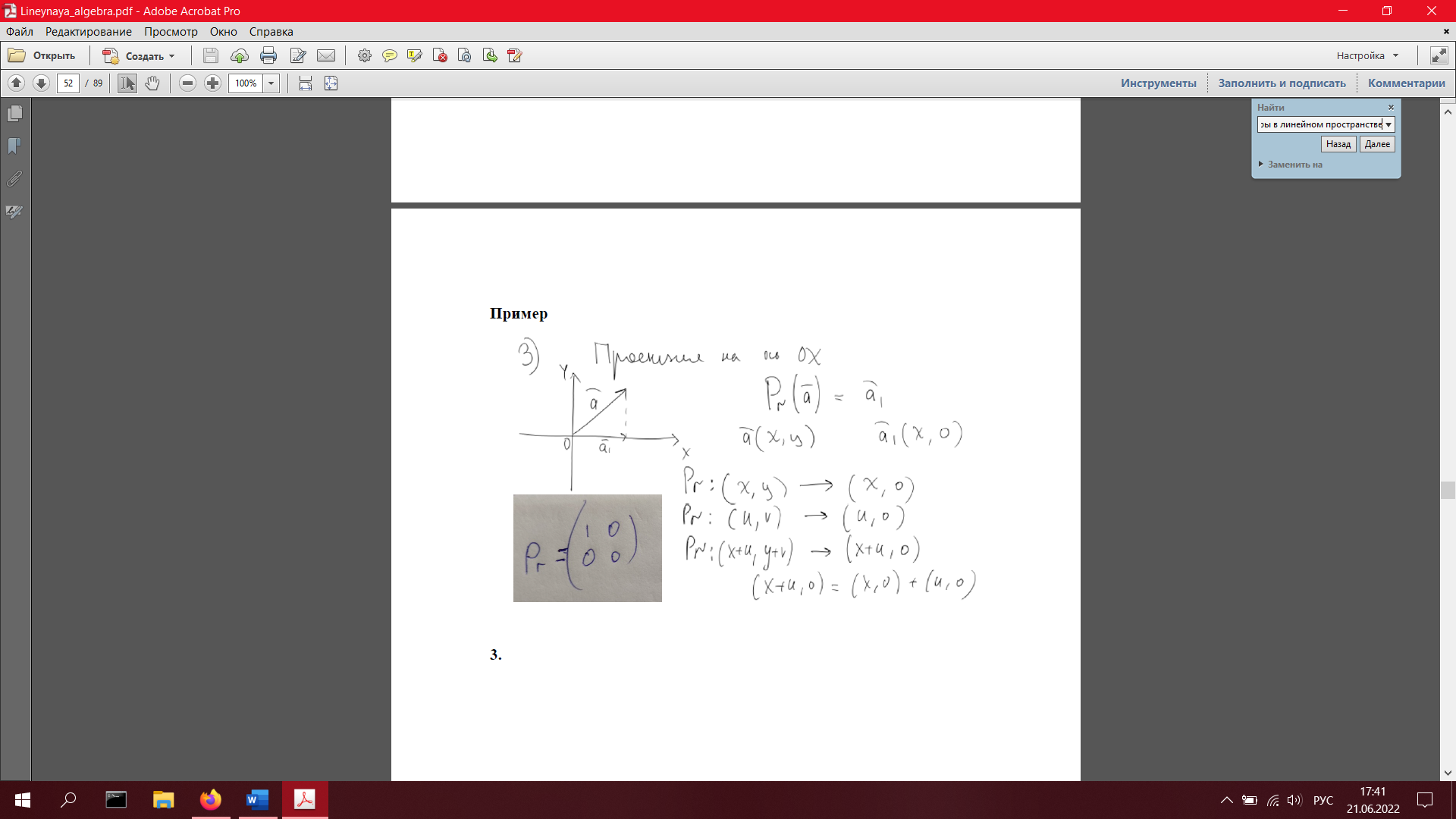
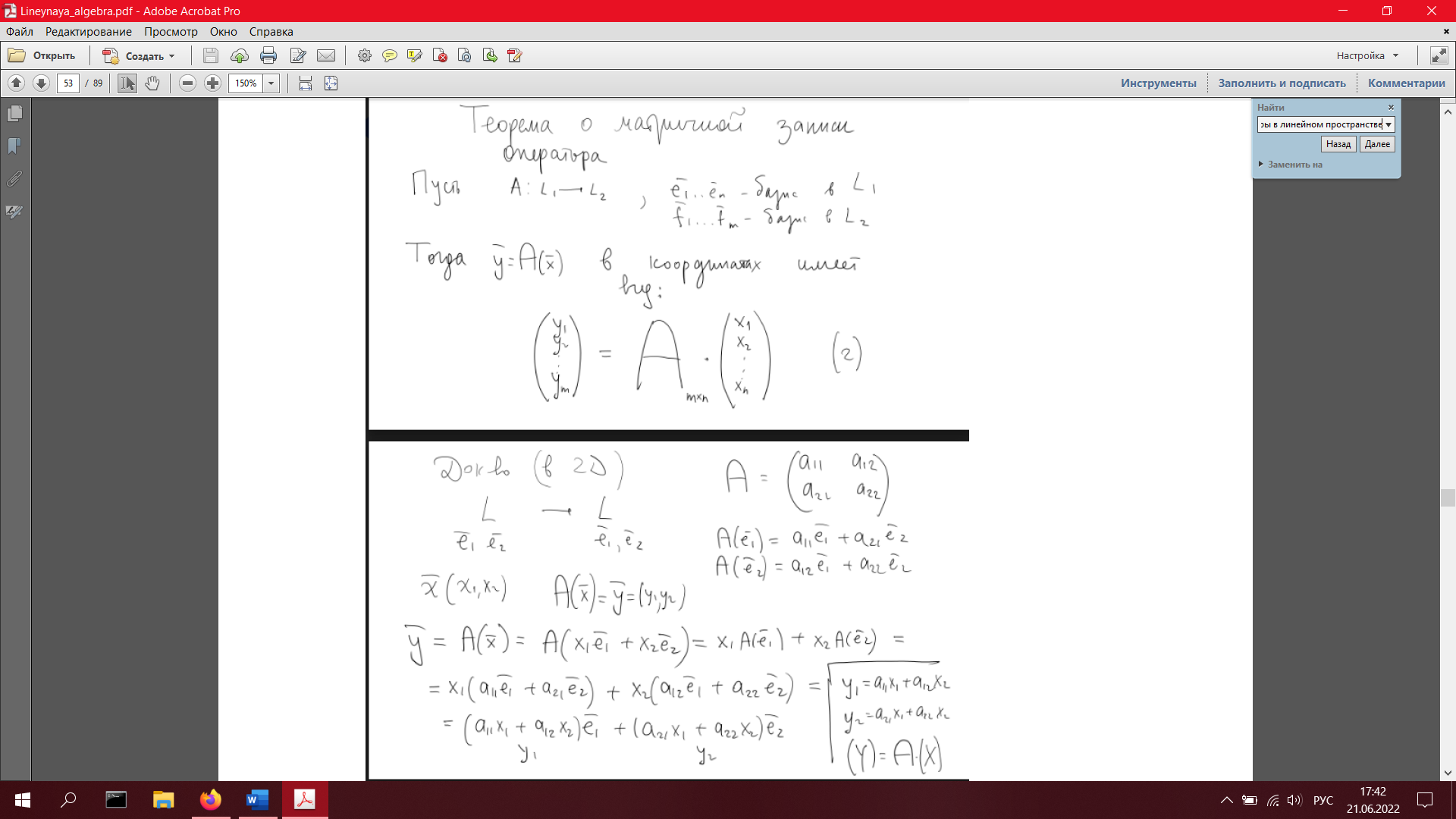
19. Линейные операторы в линейном пространстве. Матрица оператора. Примеры операторов и соответствующих матриц. Теорема о матричной записи линейного оператора (с доказательством в размерности 2).

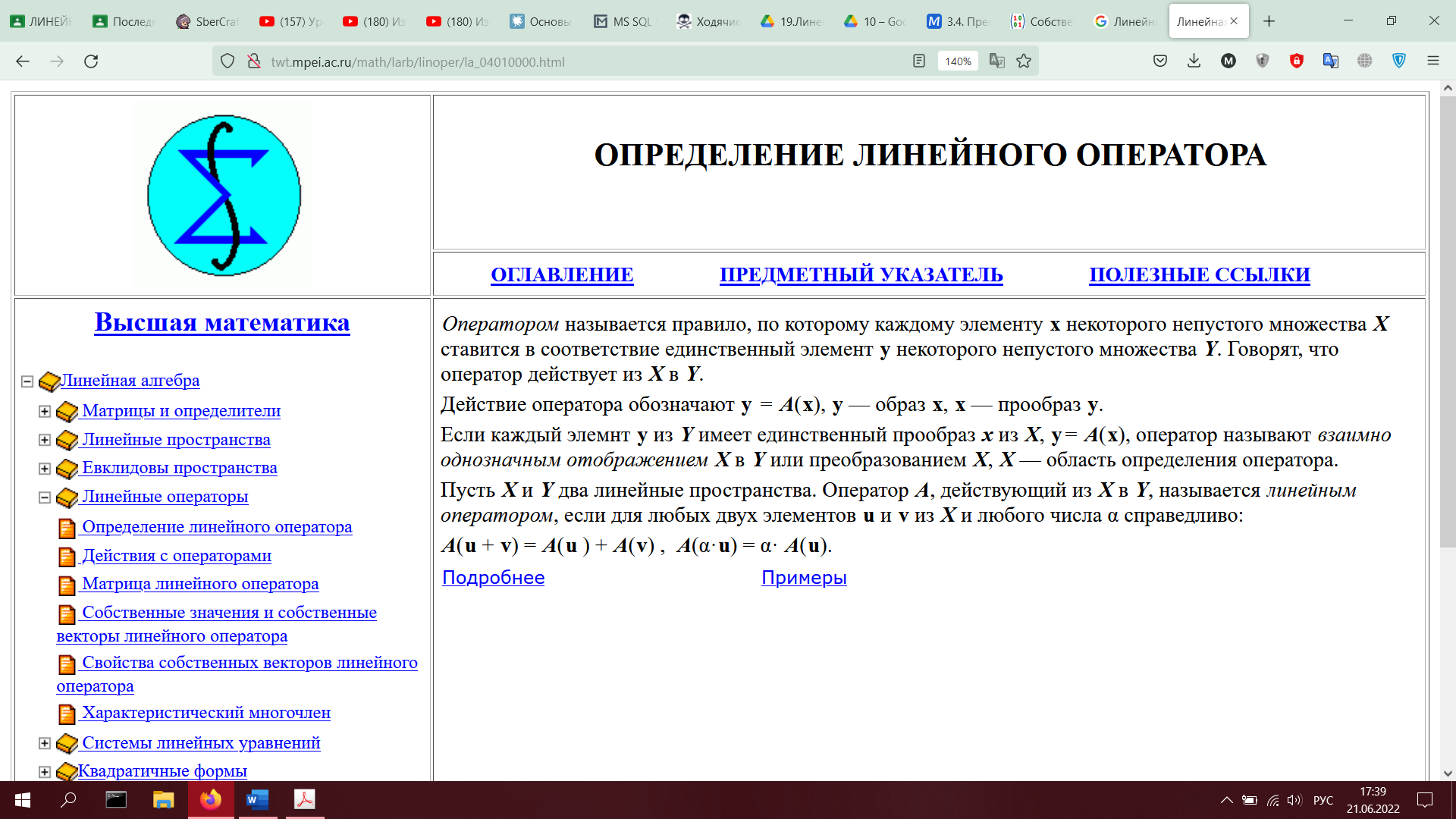
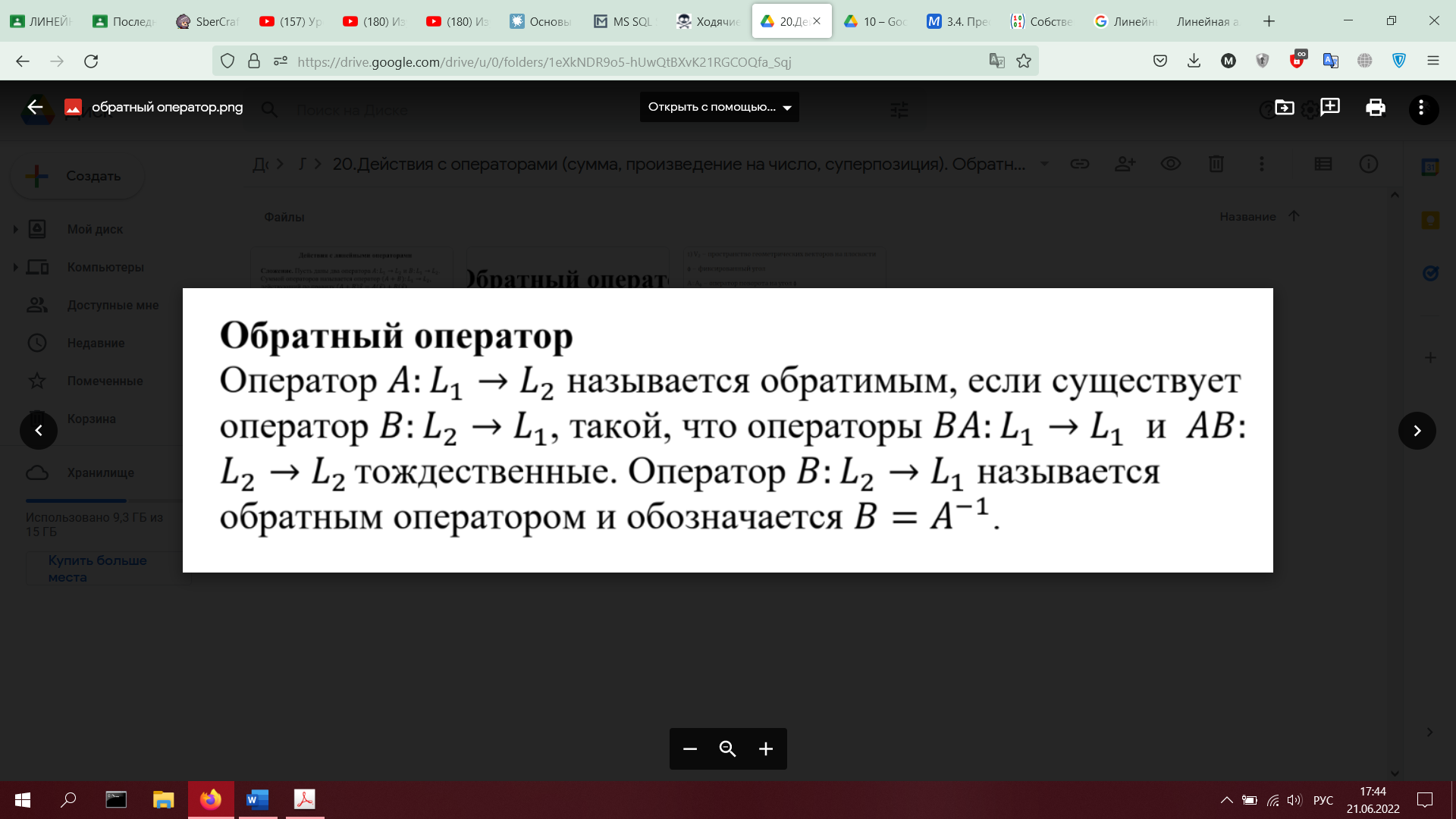
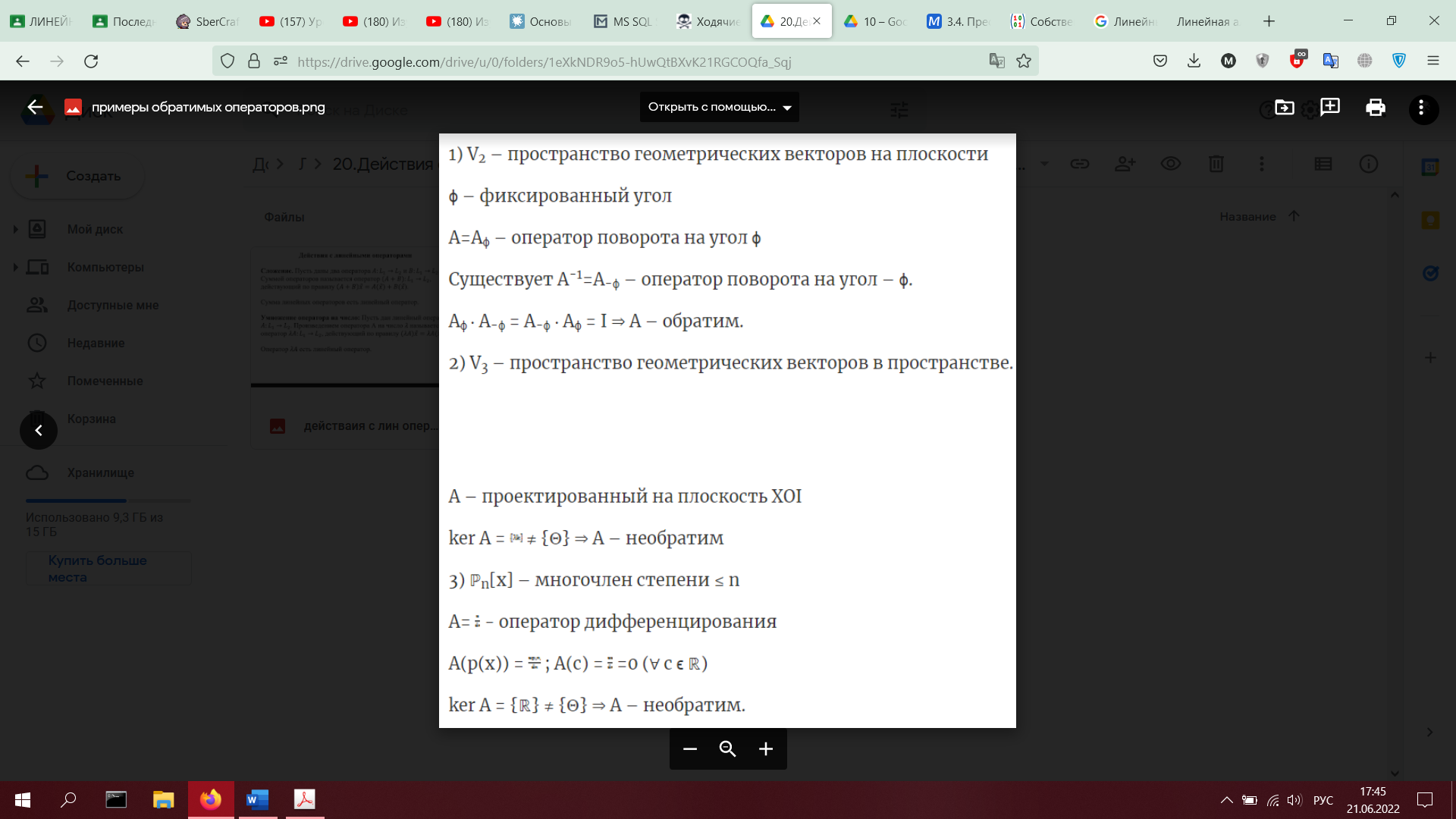
20. Действия с операторами (сумма, произведение на число, суперпозиция). Обратный оператор.(определения и примеры)

21. Ядро и образ линейного оператора. Теорема о размерности ядра и образа линейного оператора (с доказательством).

ИЛИ

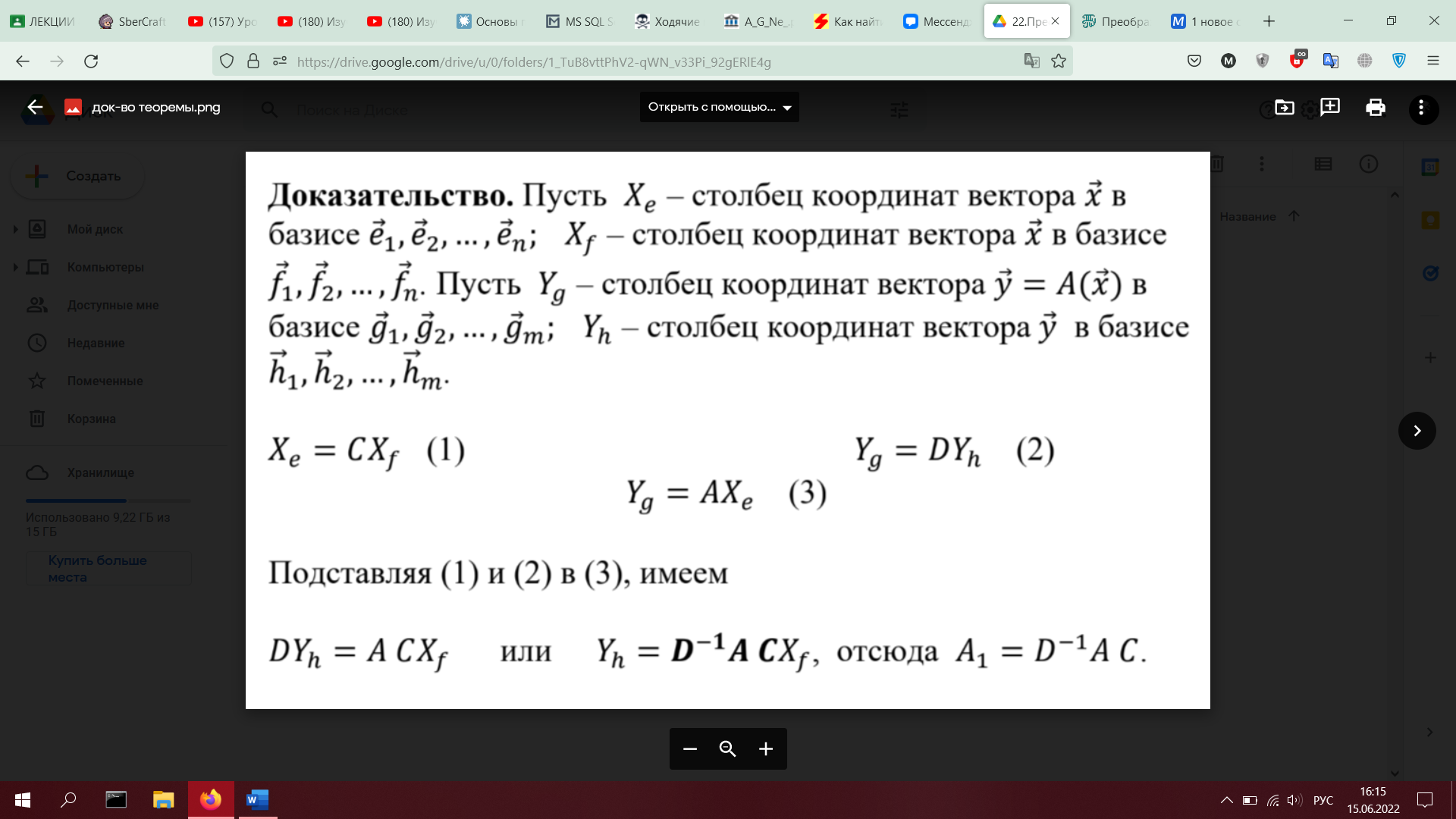
22. Преобразование матрицы оператора при переходе к новому базису (с доказательством).

23. Собственные векторы и собственные значения линейного оператора. Алгоритм нахождения собственных векторов.

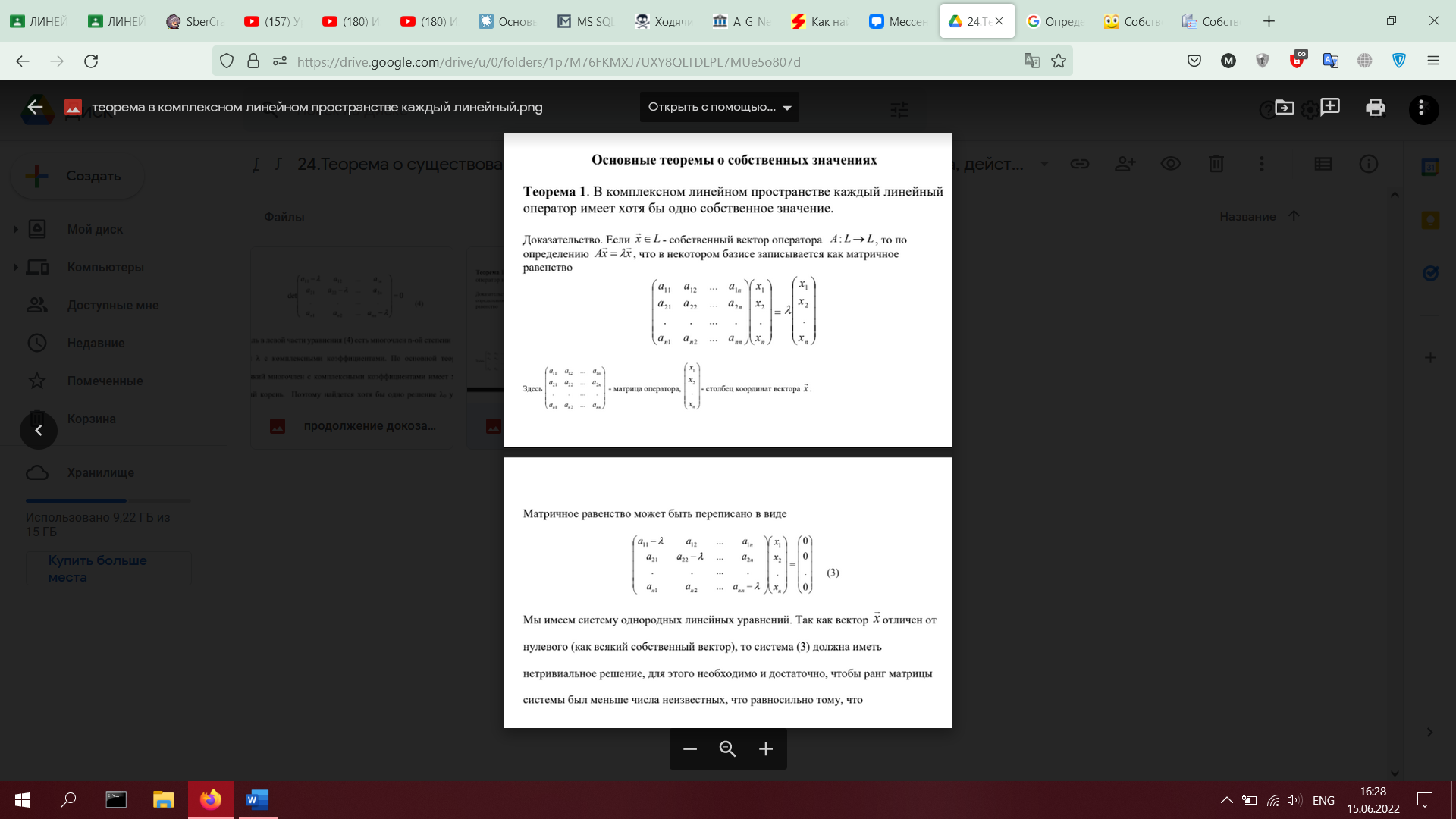
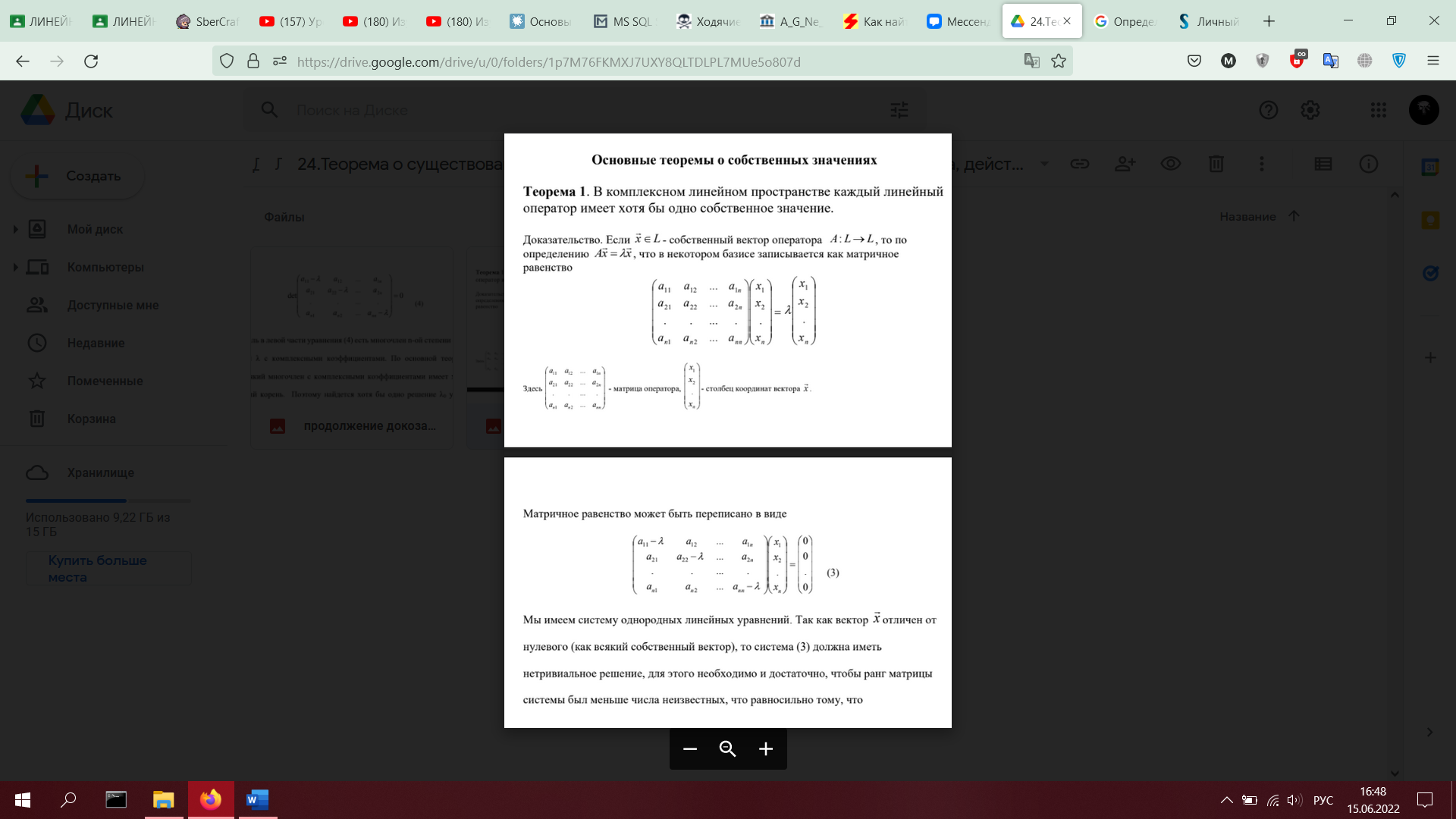
24. Теорема о существовании хотя бы одного собственного значения у оператора, действующего в комплексном линейном пространстве (с доказательством).

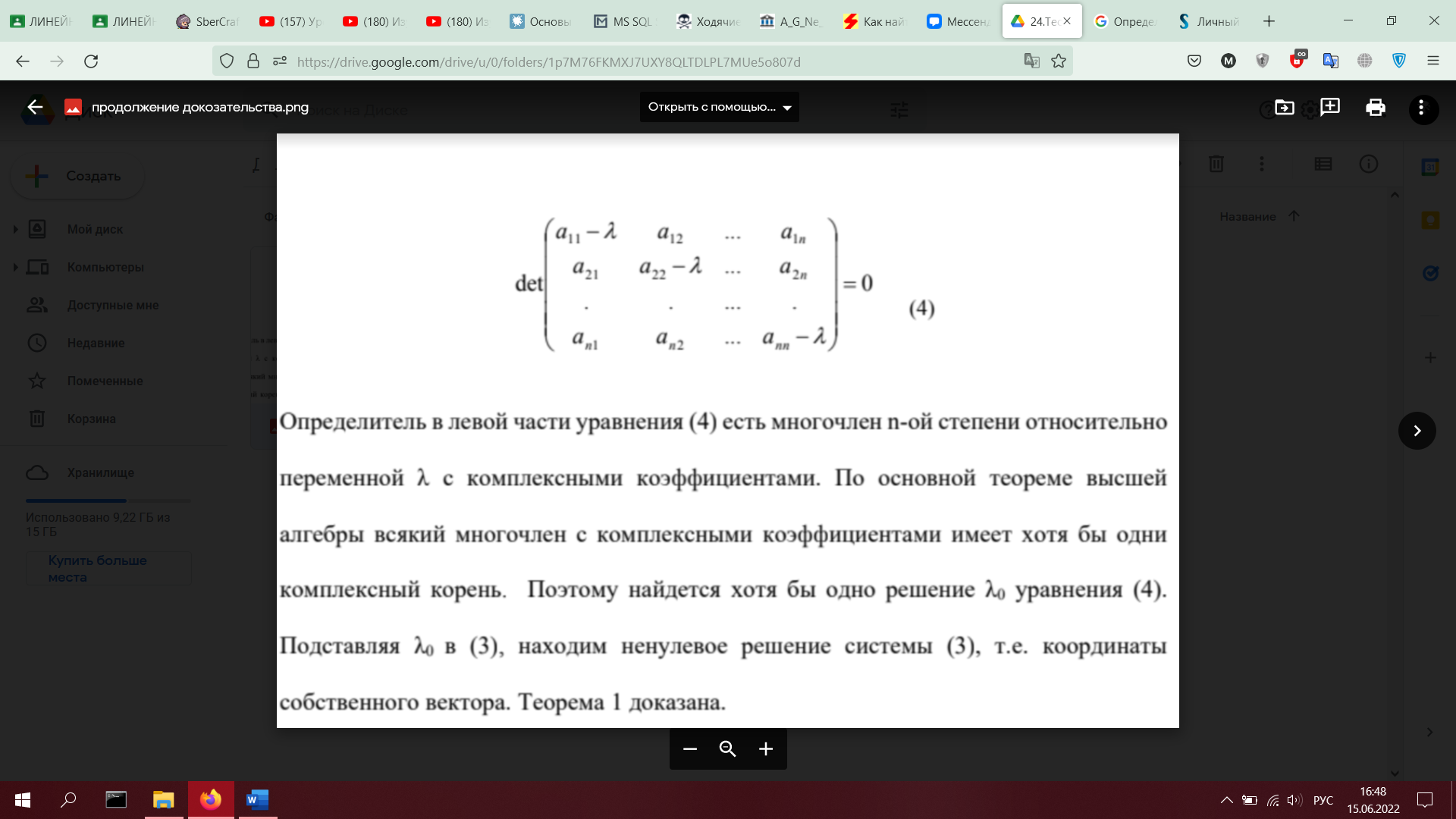
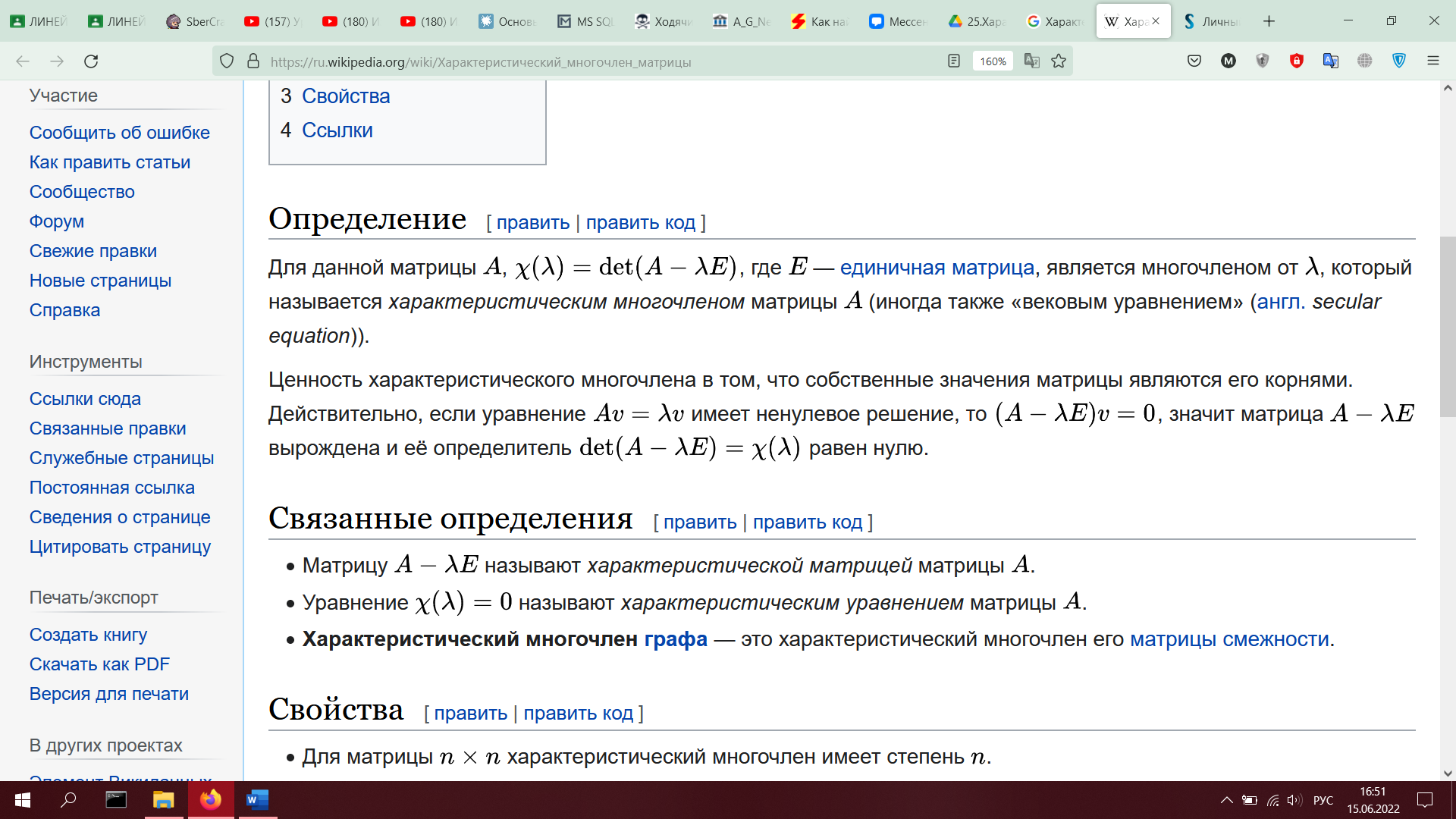
25. Характеристический многочлен, его инвариантность (с доказательством).

Характеристический многочлен матрицы — многочлен, определяющий её собственные значения.

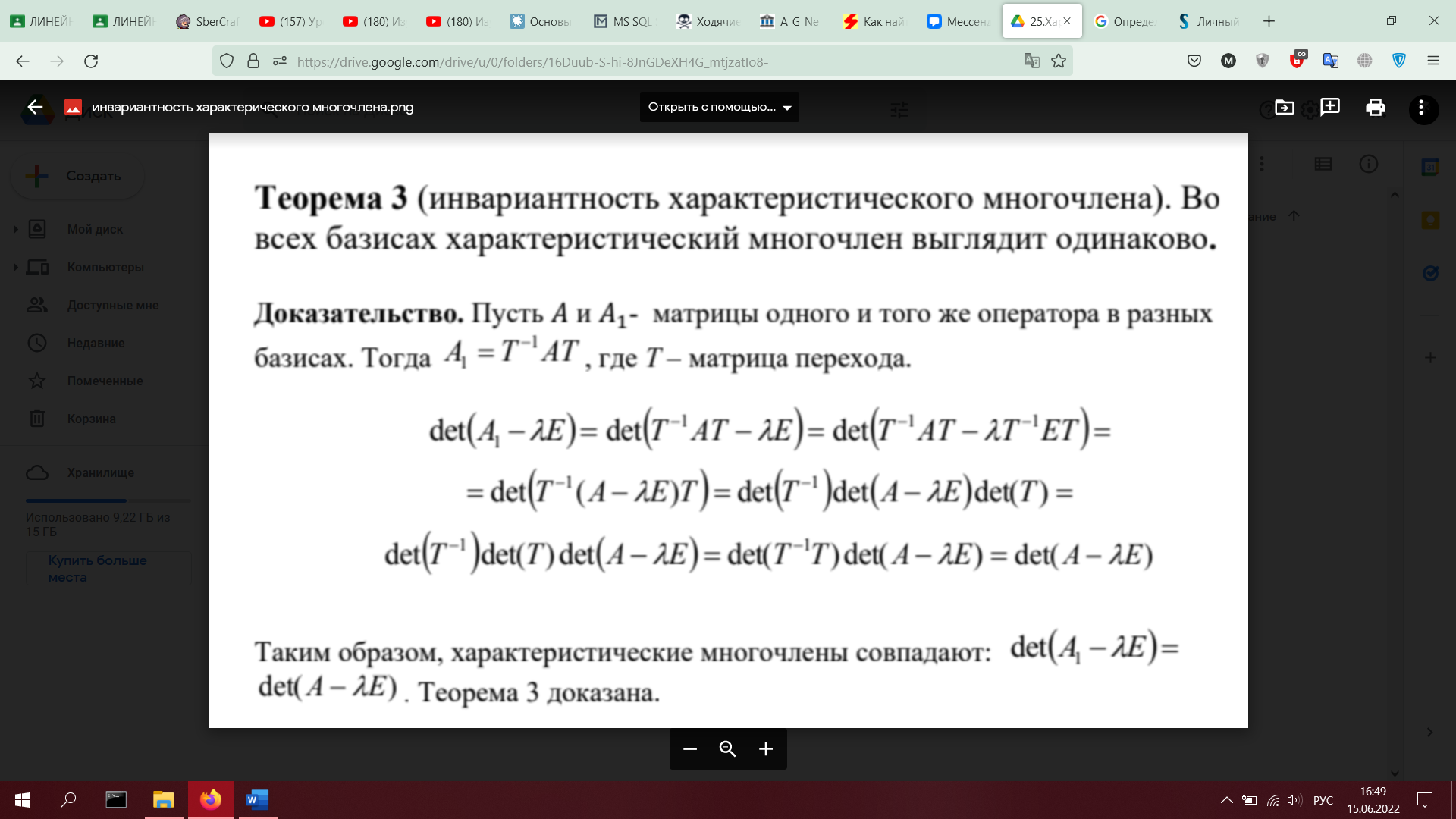
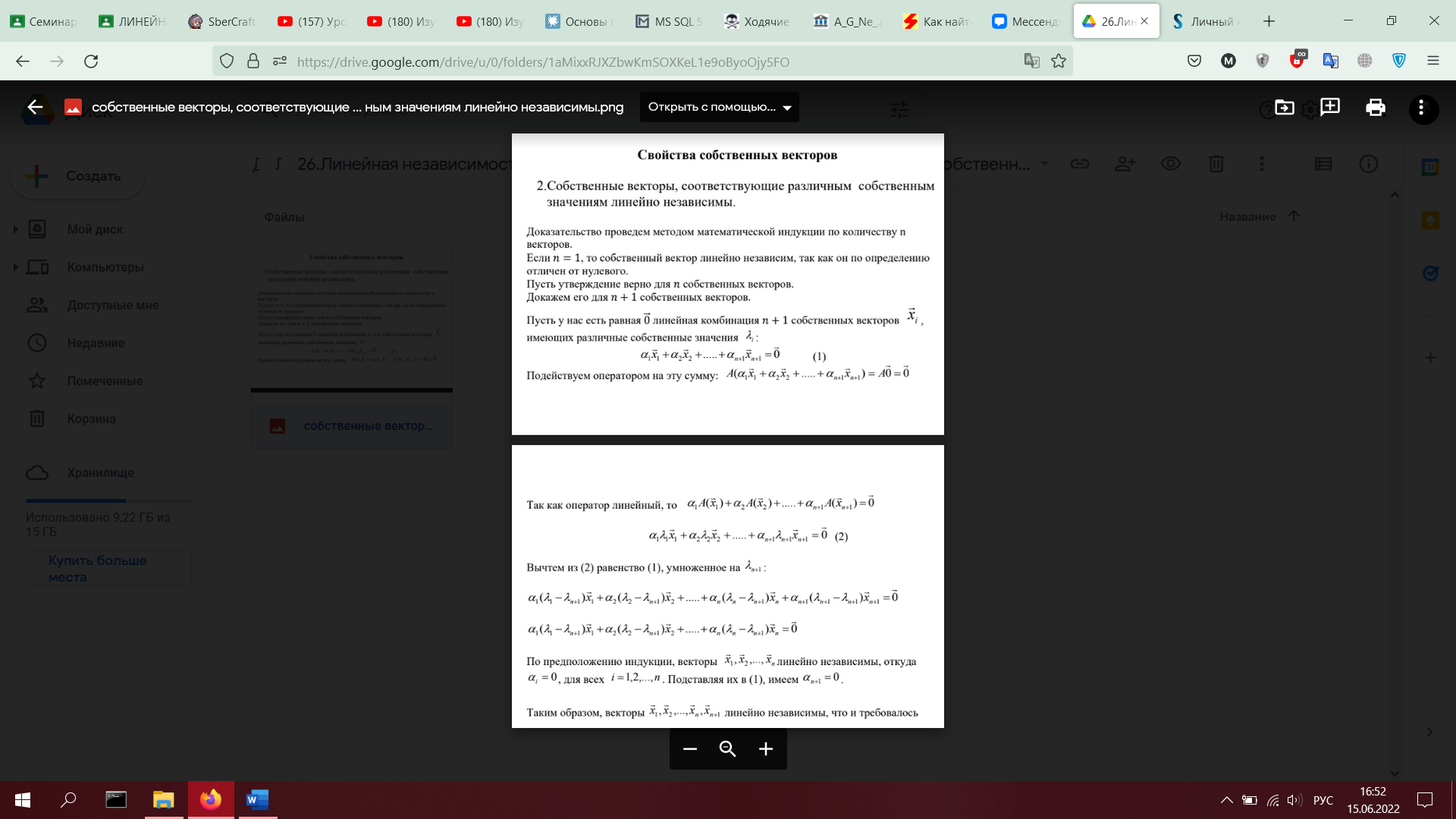
26. Линейная независимость собственных векторов, соответствующих разным собственным значениям (с доказательством).

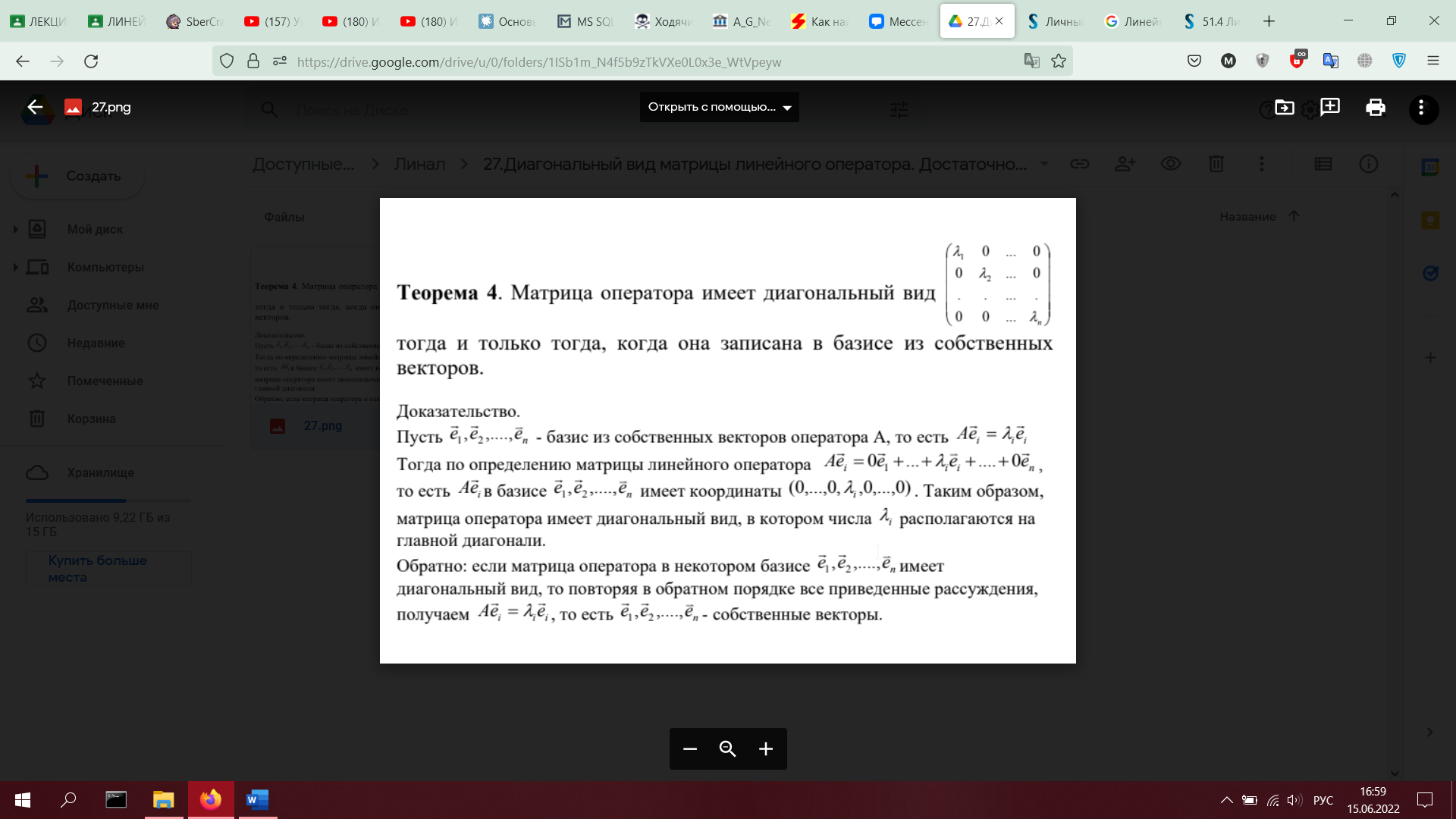
27. Диагональный вид матрицы линейного оператора. Достаточное условие приводимости матрицы оператора к диагональному виду (с доказательством).

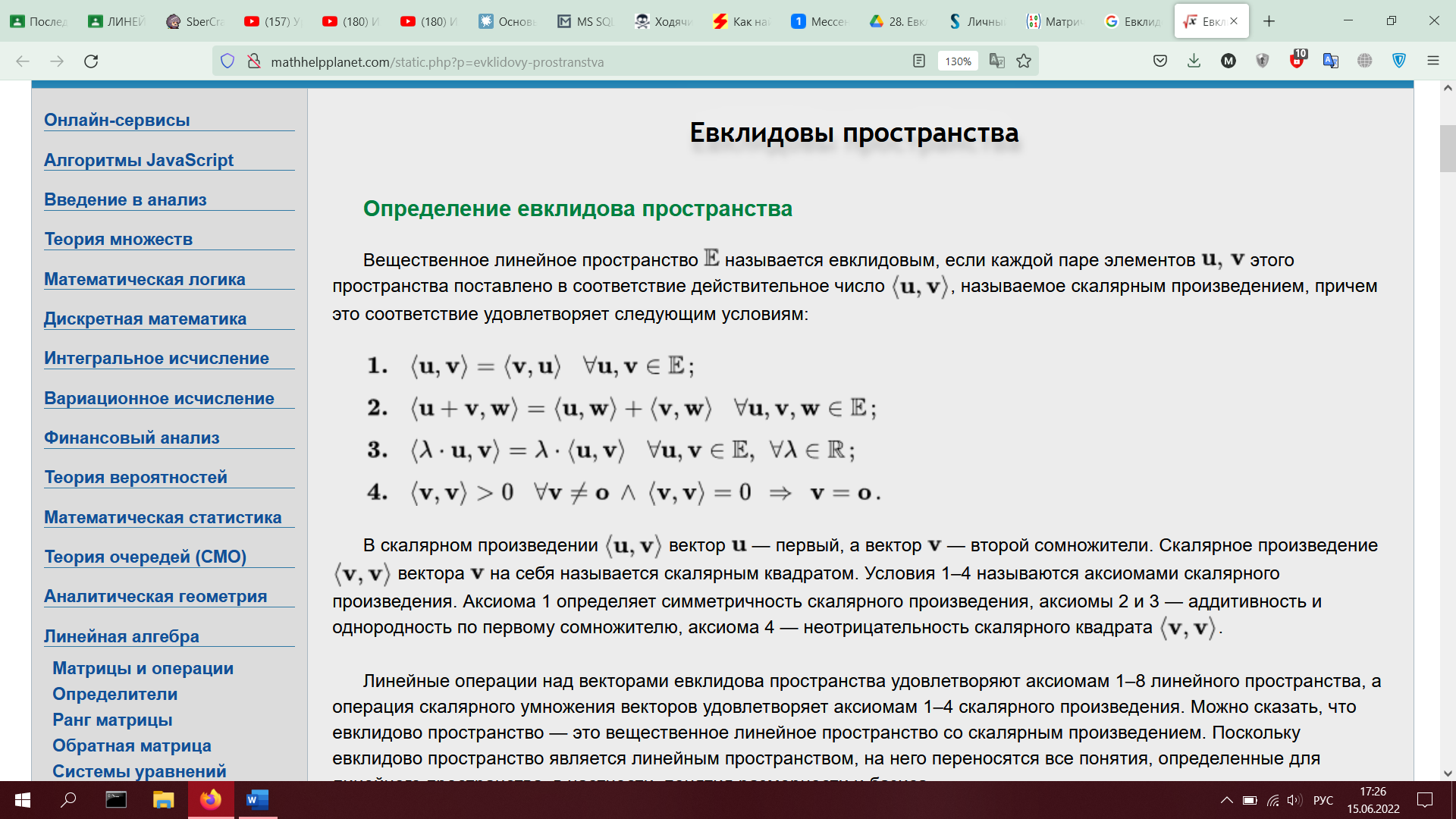
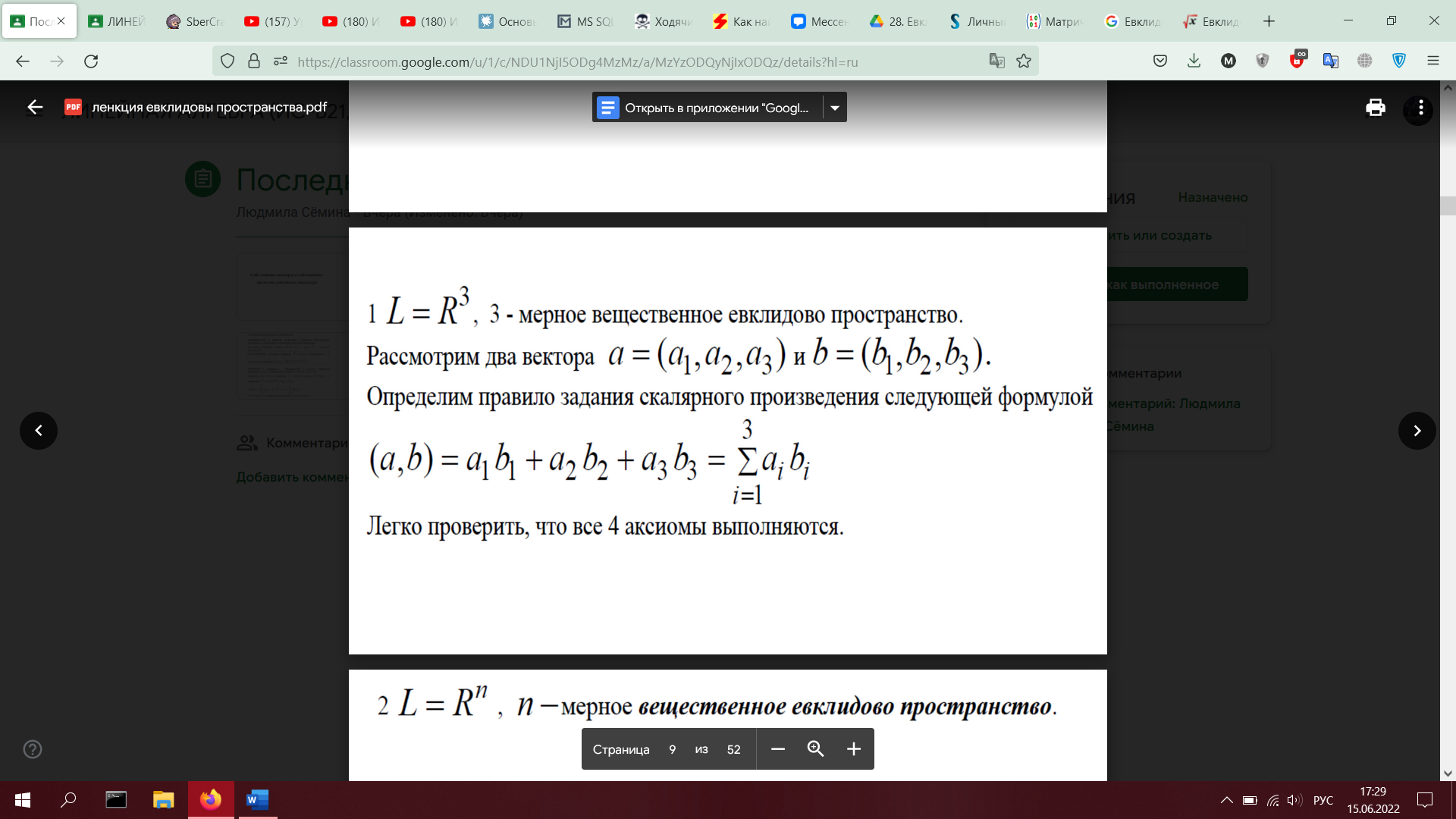
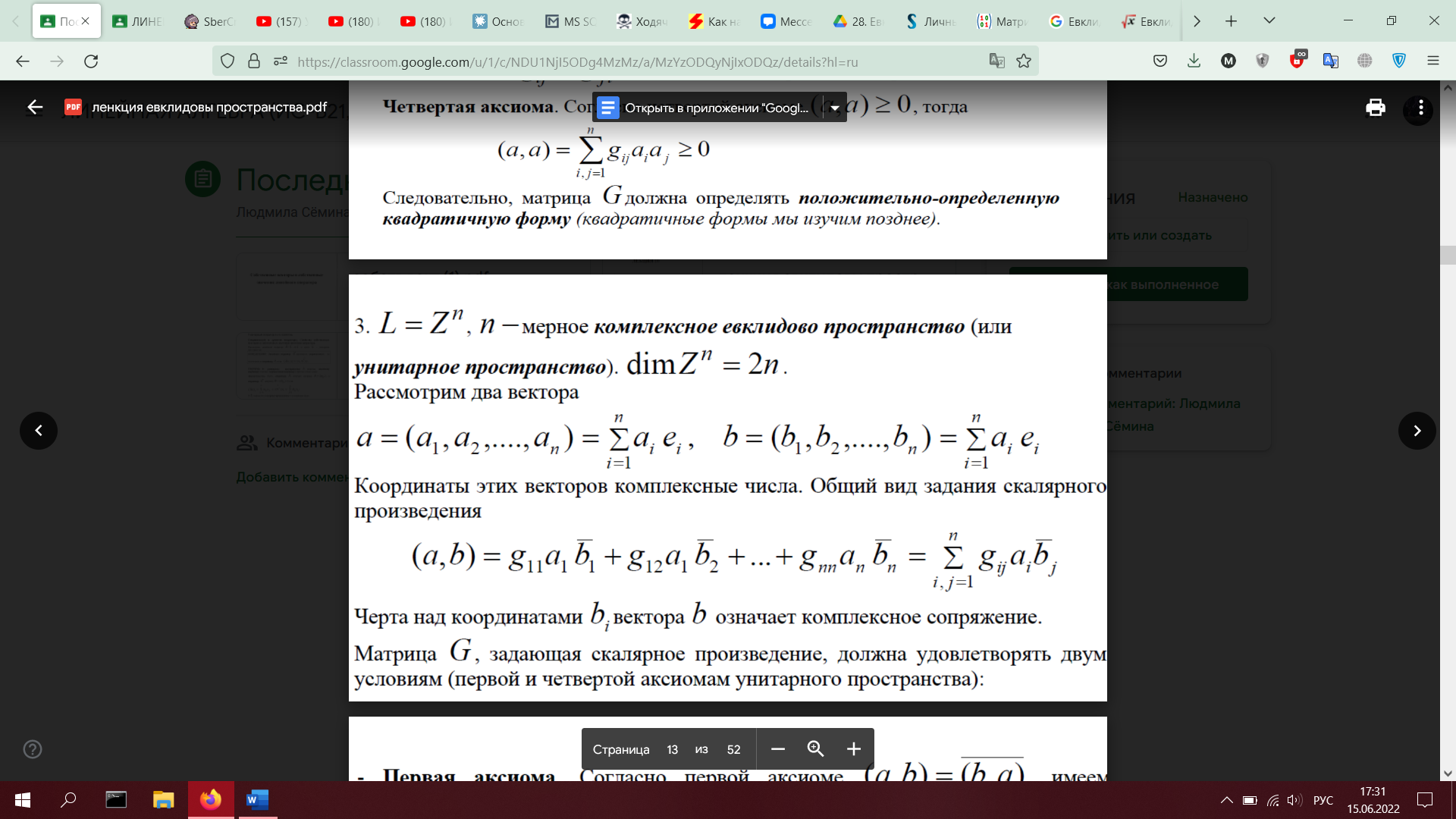
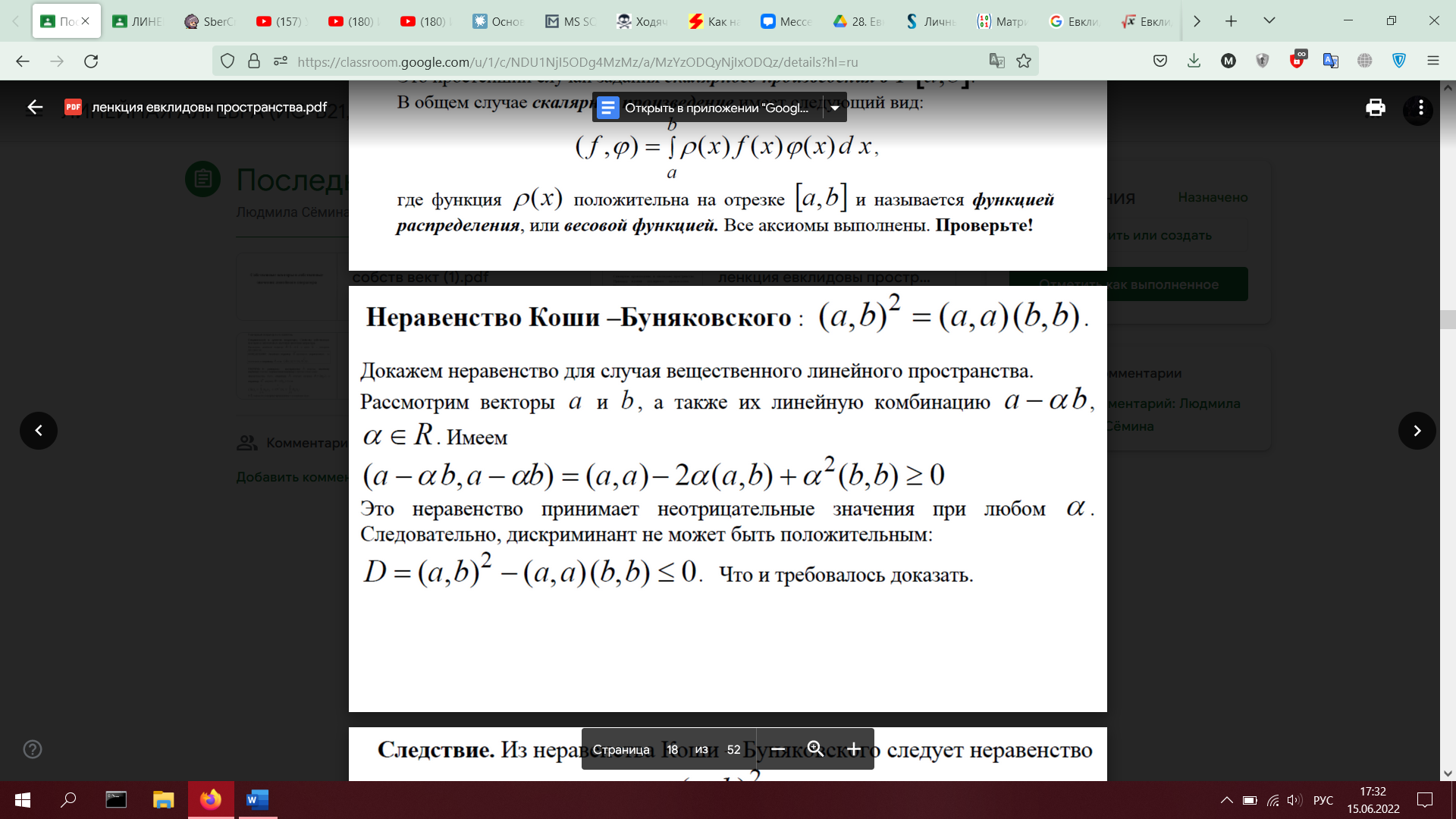
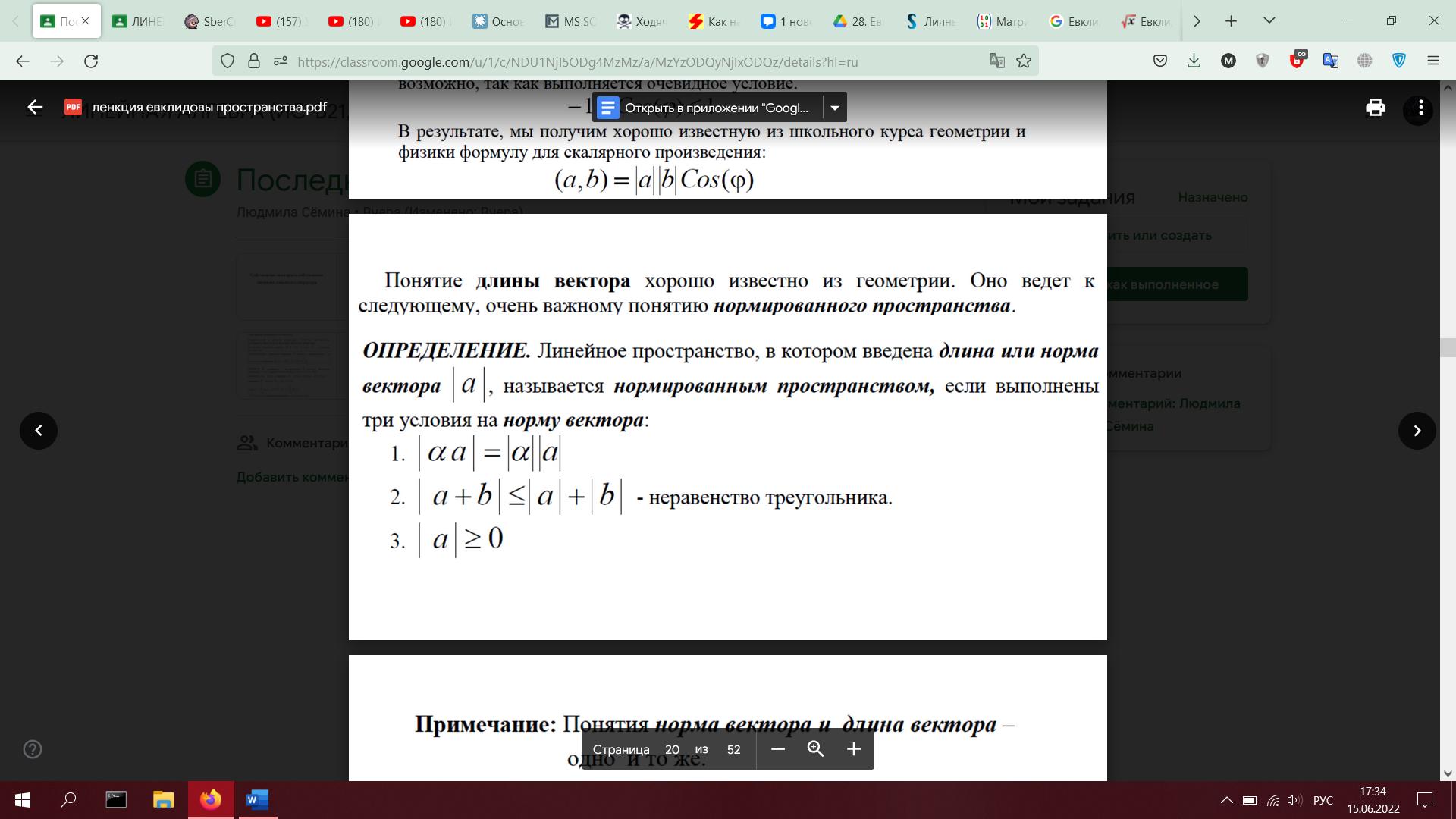
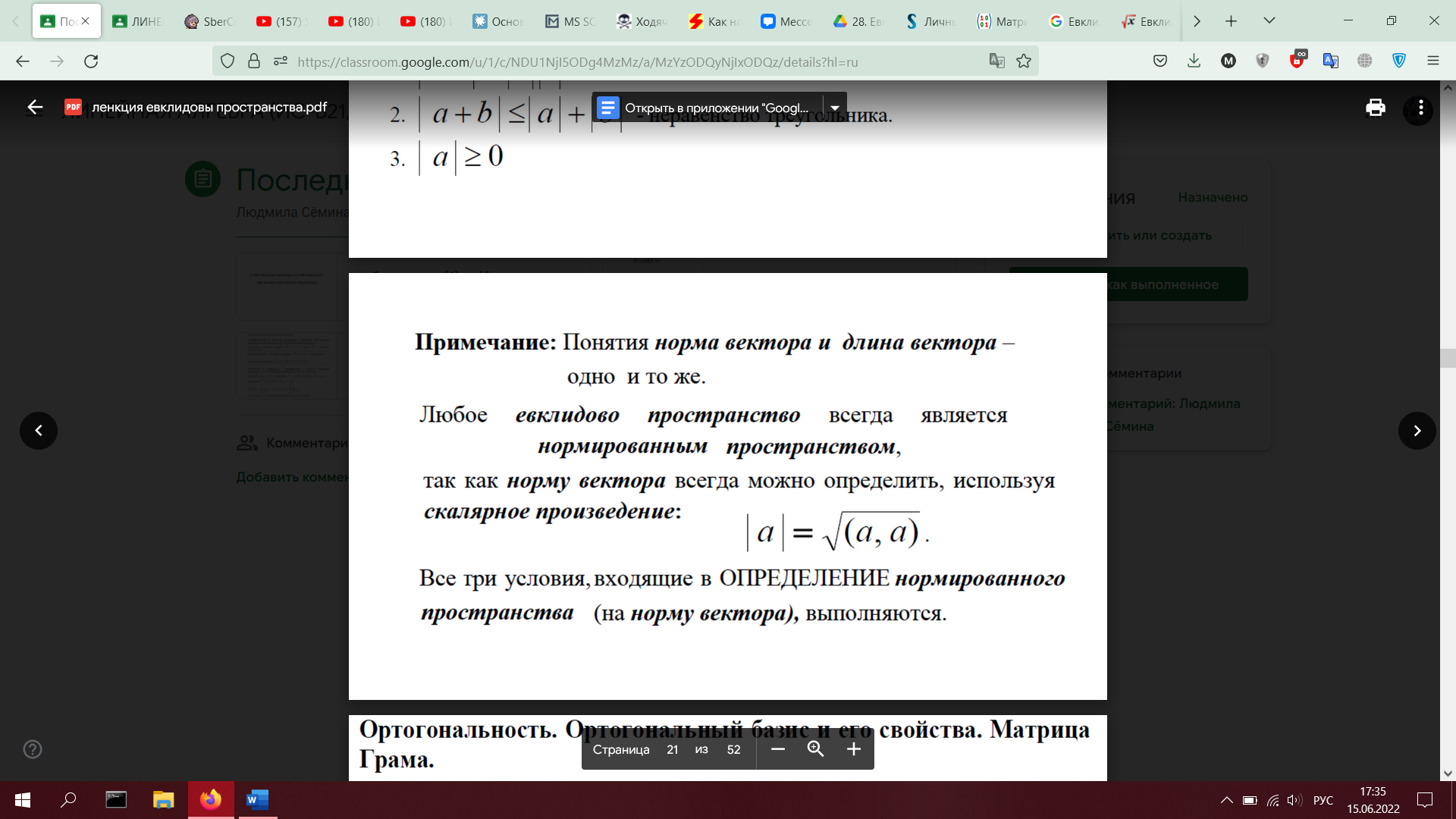
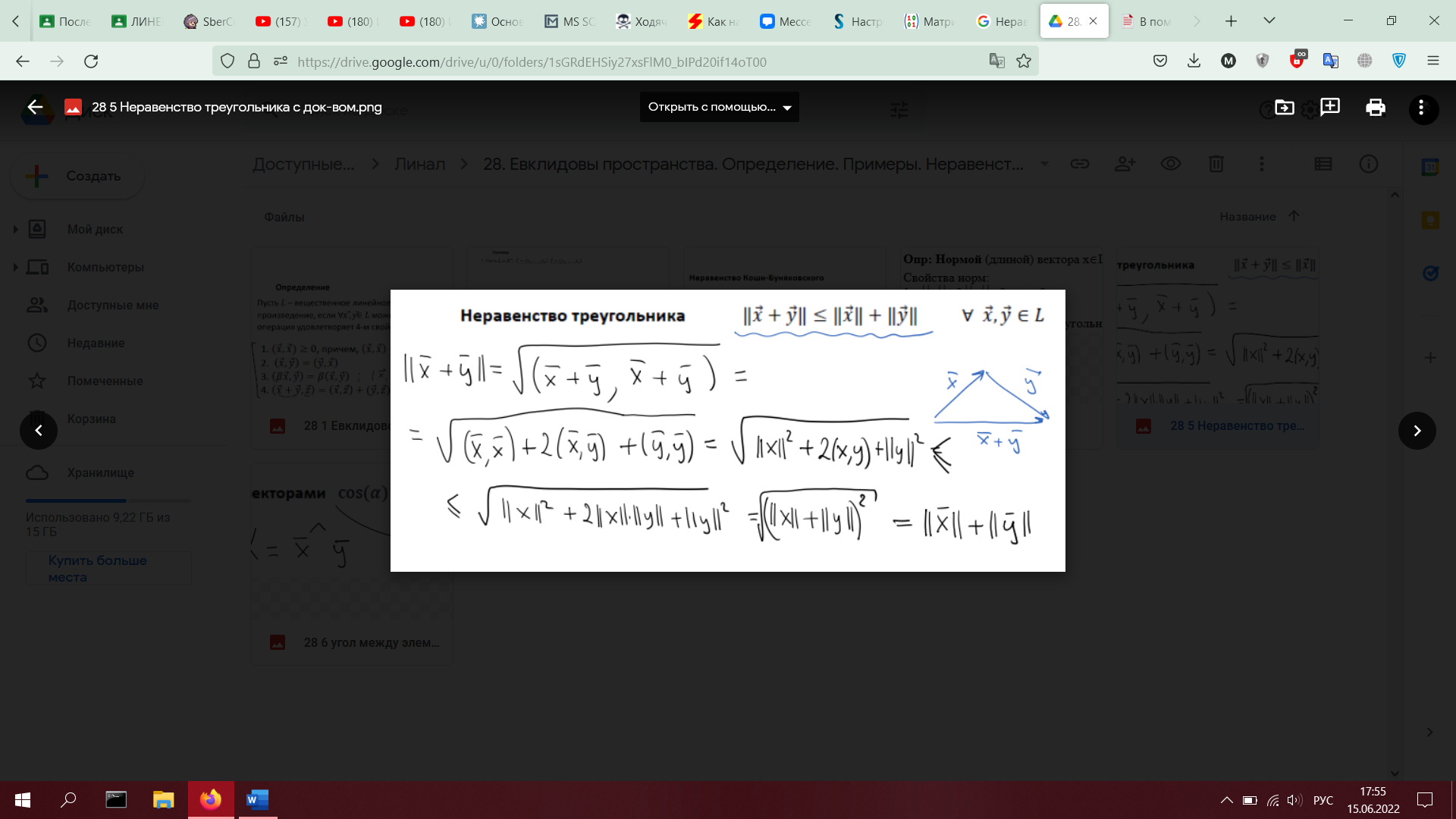
28. Евклидовы пространства. Определение. Примеры. Неравенство Коши-Буняковского. Норма элемента. Неравенство треугольника. Угол между элементами (доказать оба неравенства)

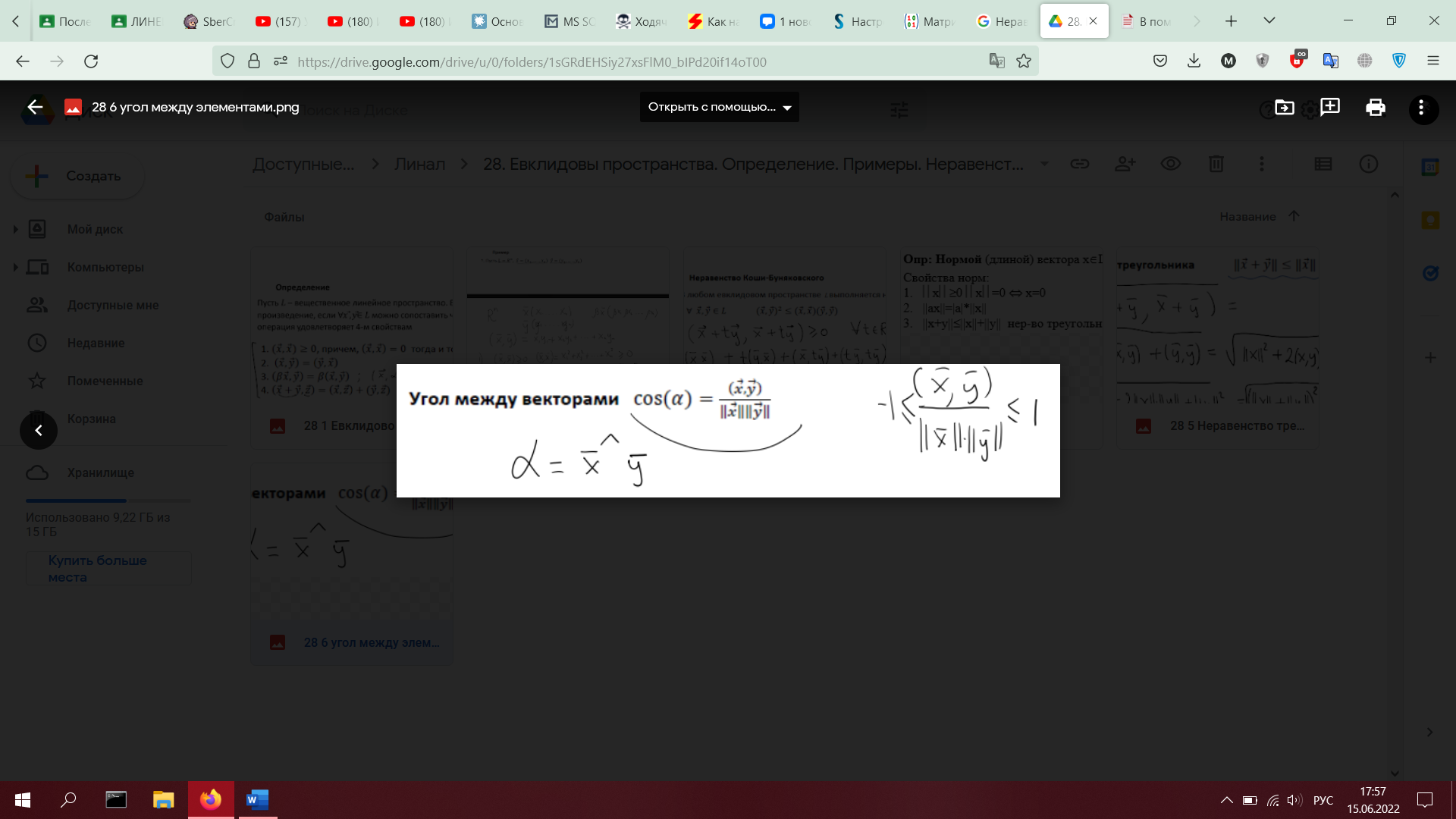
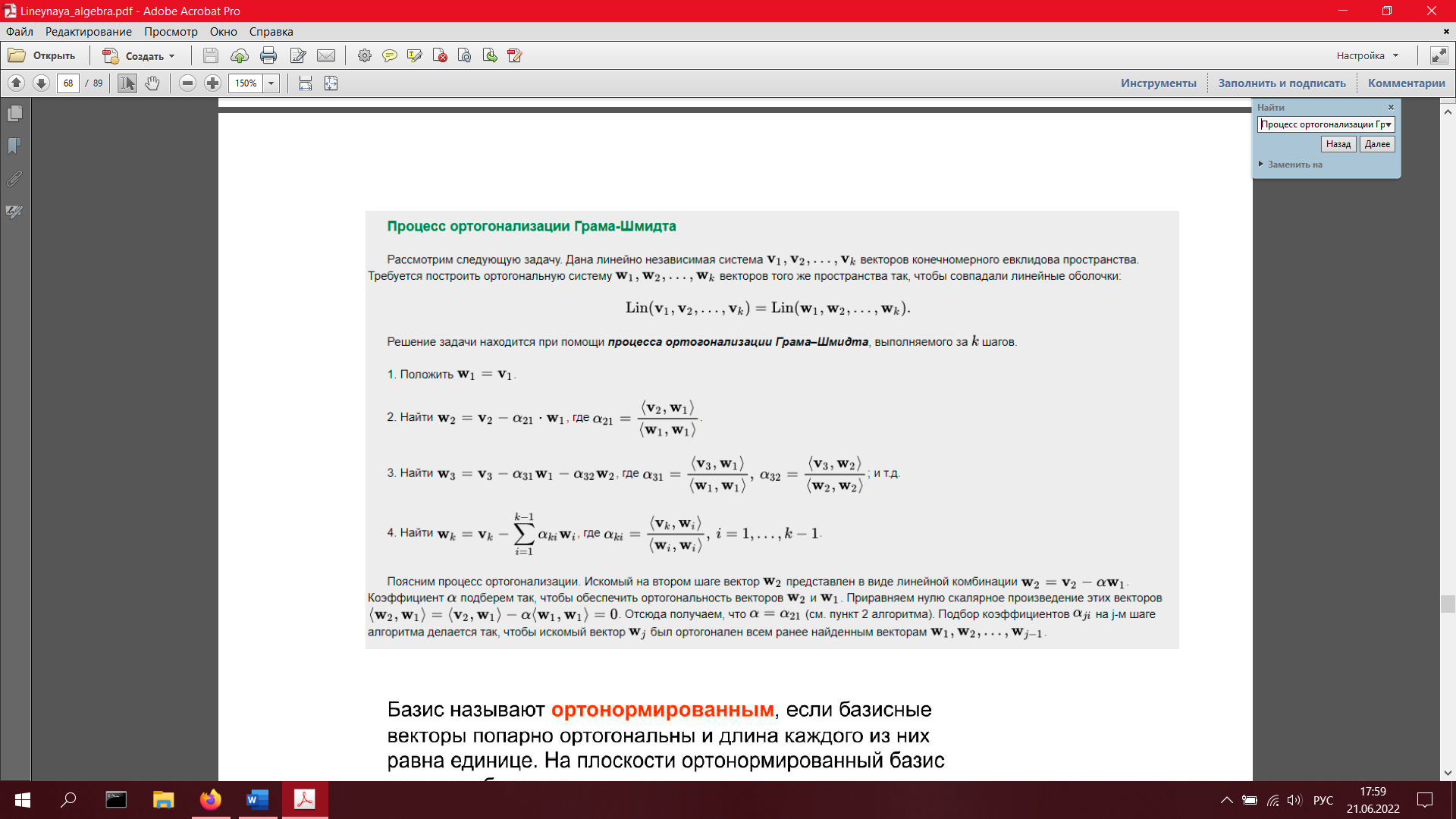
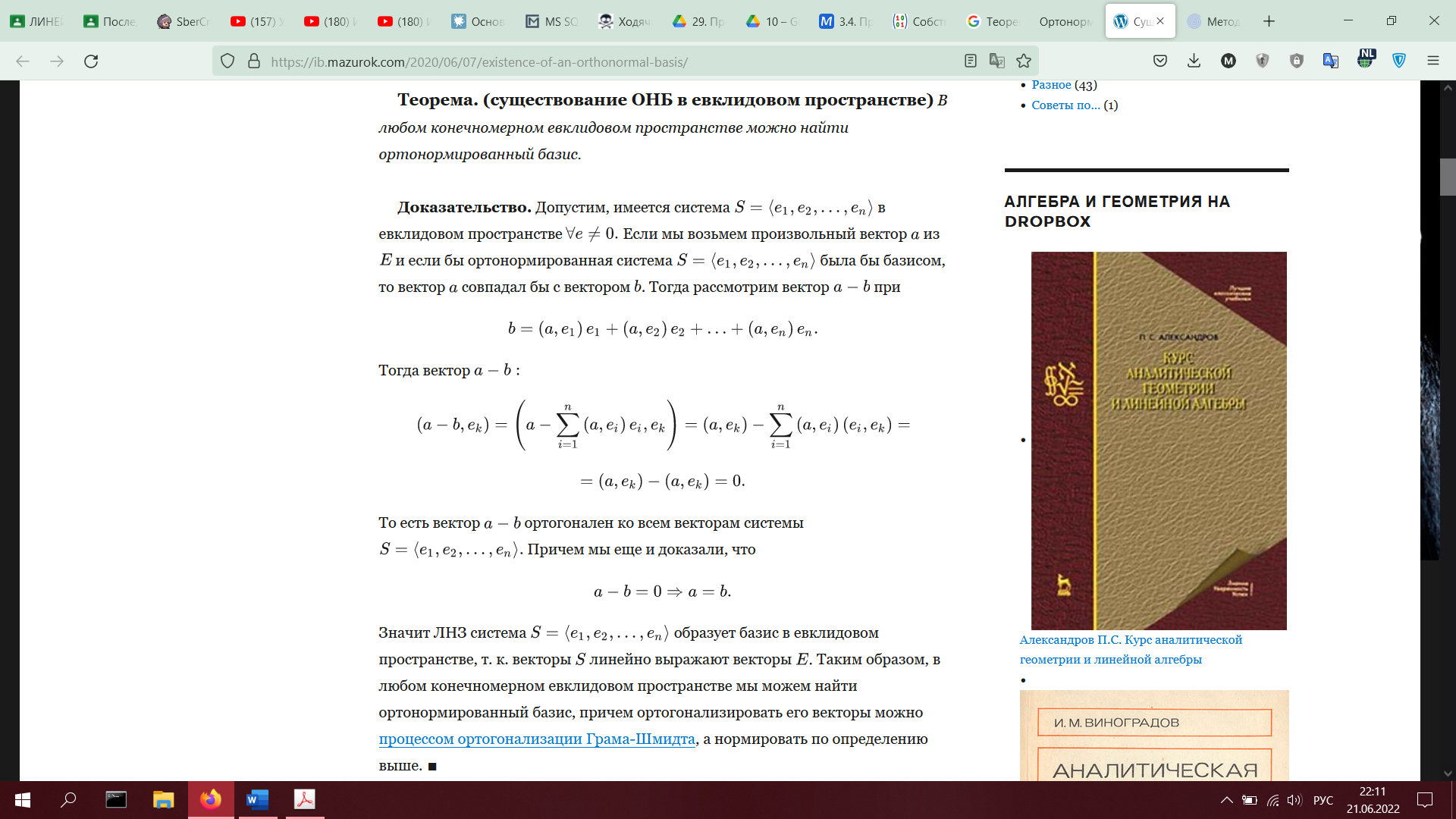
29. Процесс ортогонализации Грама-Шмидта. Ортонормированный базис. Теорема о существовании ортонормированного базиса в конечномерном пространстве (с доказательством).

ИЛИ

30. Матрица Грама и её применение к вычислению скалярных произведений (показать на примере)

ОБЩЕЕ ПОНЯТИЕ О МАТРИЦЕ ГРАММА , ЕСЛИ ДОЕБЕТСЯ

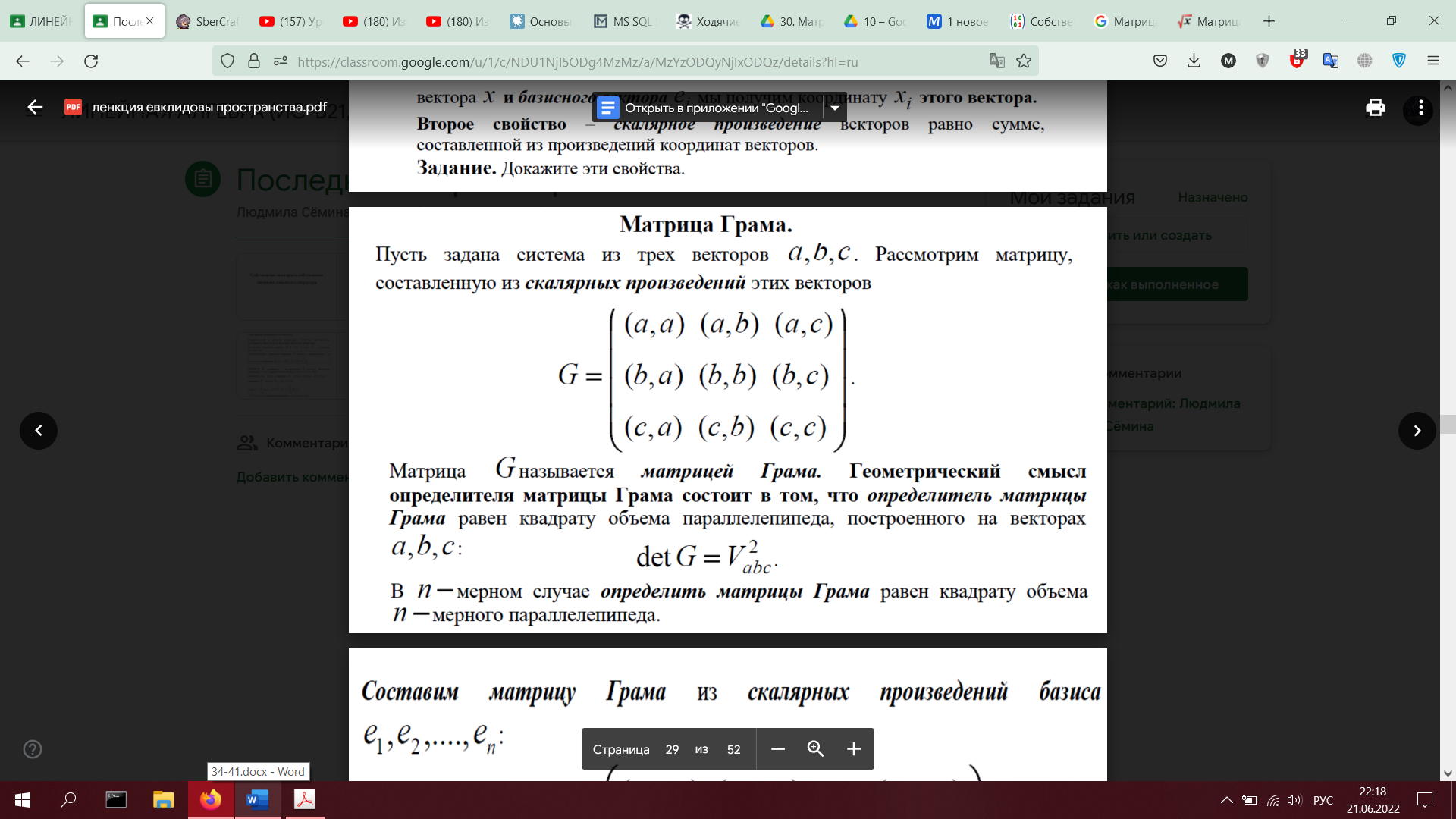
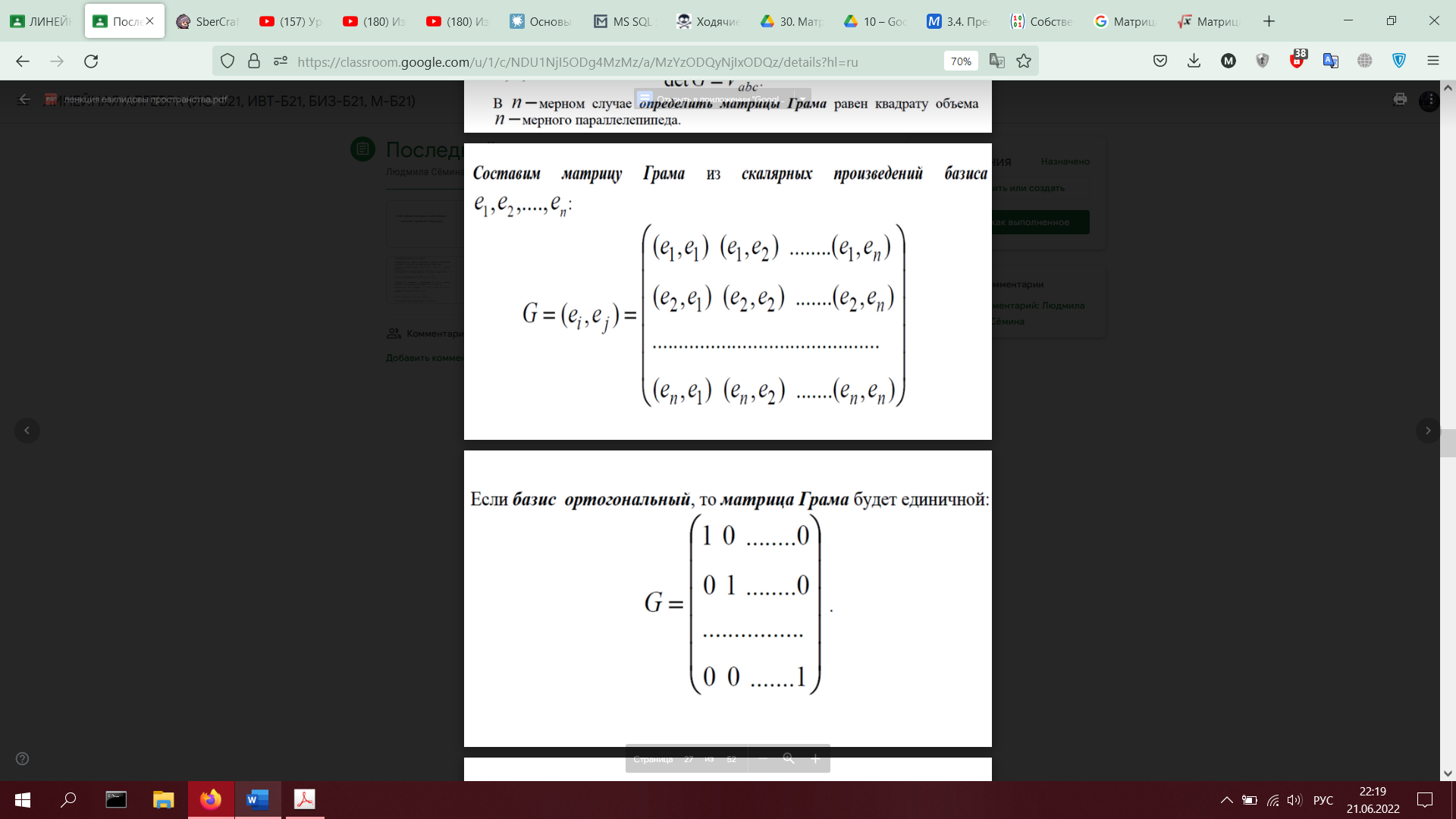
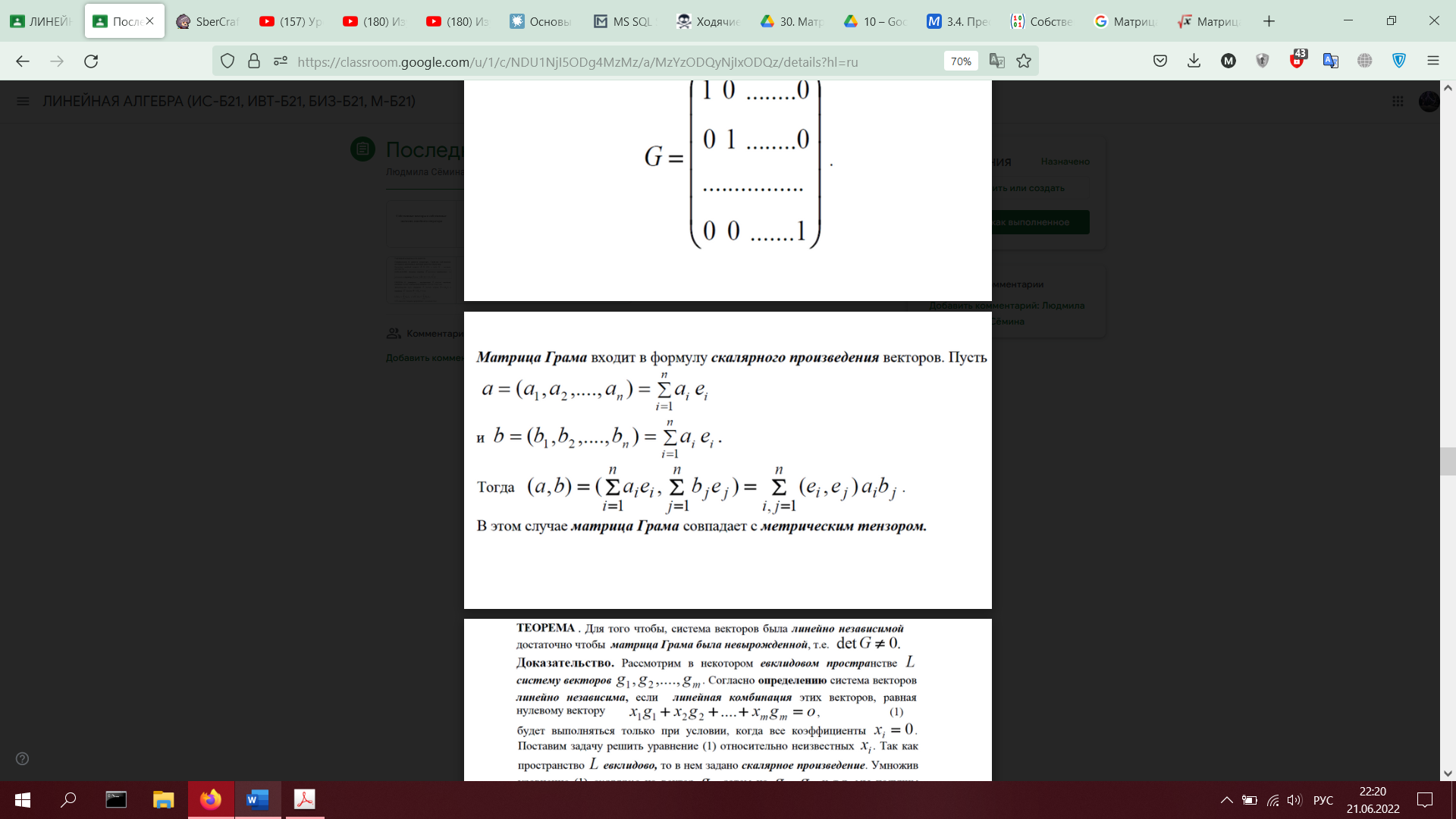
САМ ПРИМЕР

31. Вычисление объема n-мерного параллелепипеда с помощью матрицы Грама (дать определение параллелепипеда и объема, сформулировать теорему без доказательства).

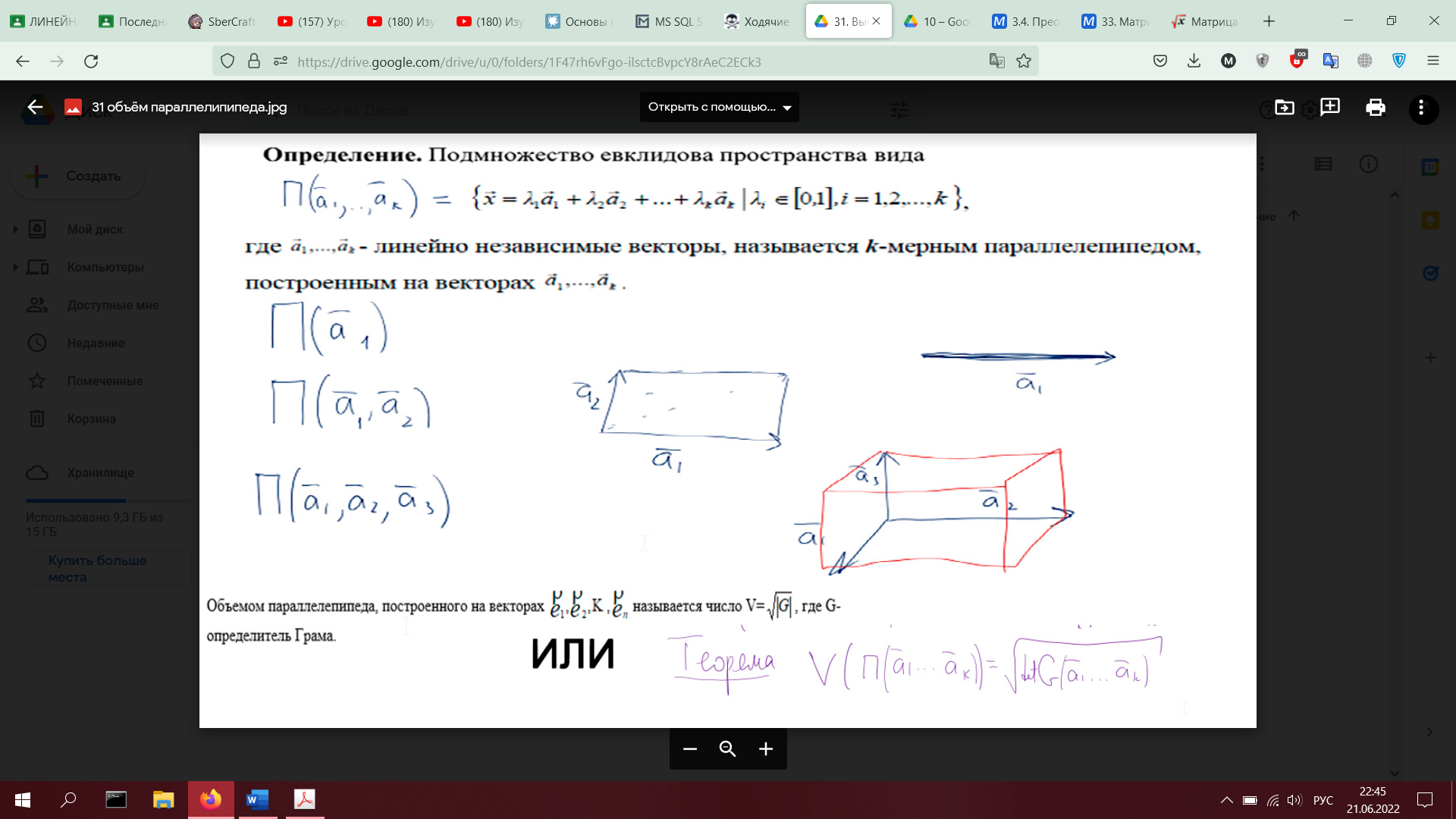
32. Ортогональное дополнение. Теорема о разложении евклидова пространства в прямую сумму любого его подпространства и ортогонального дополнения к этому подпространству (с доказательством).

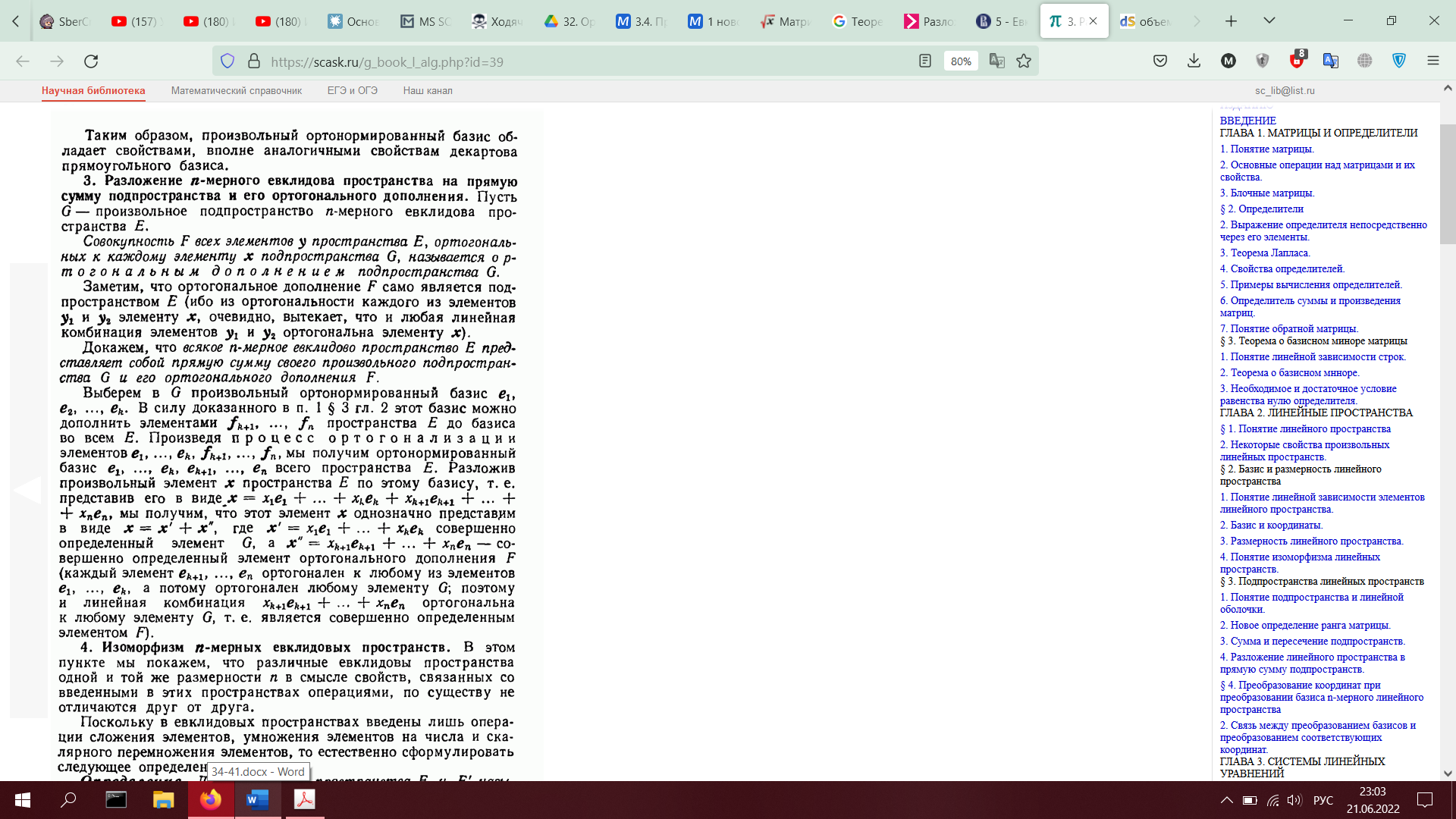
ИЛИ

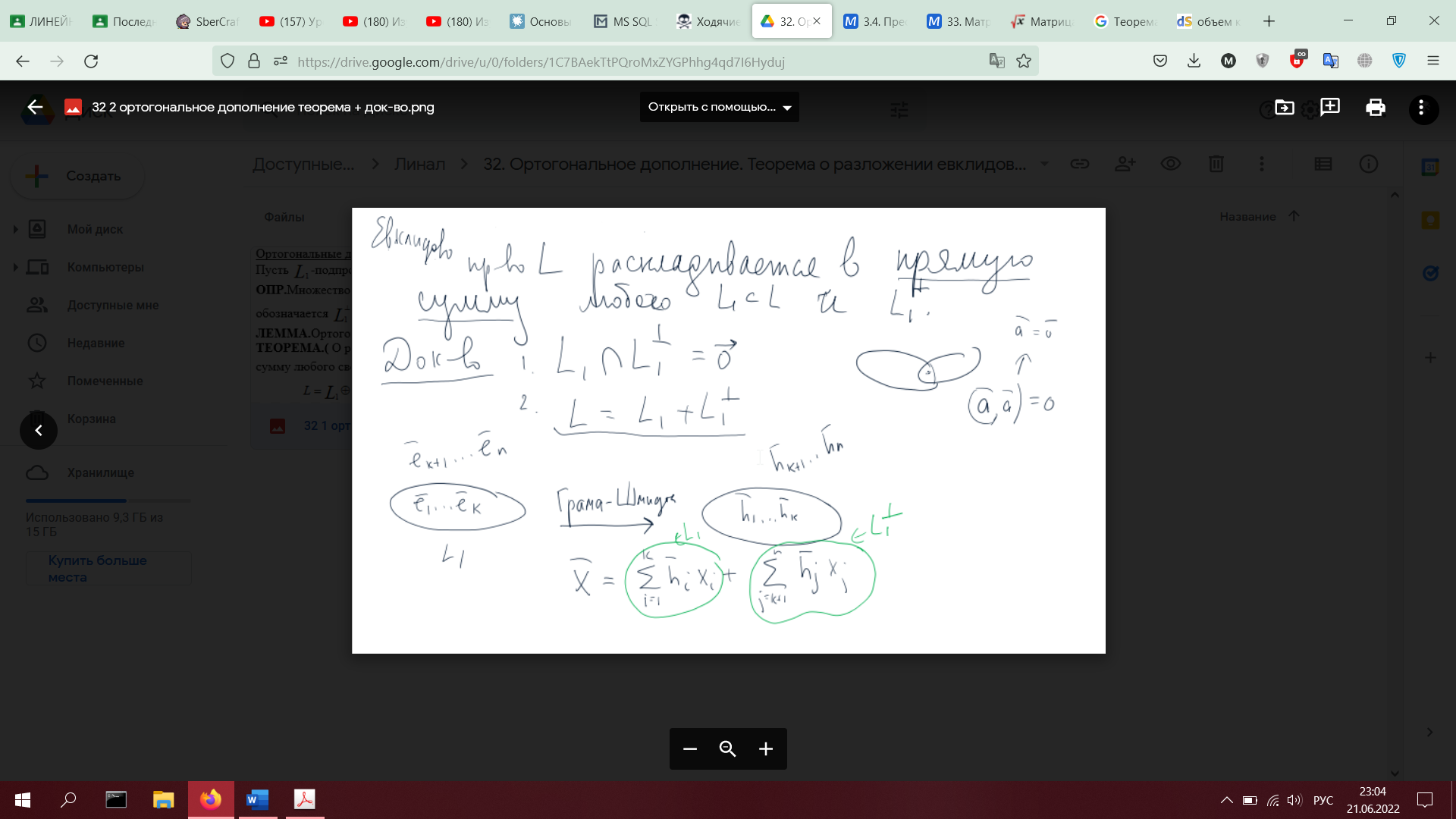
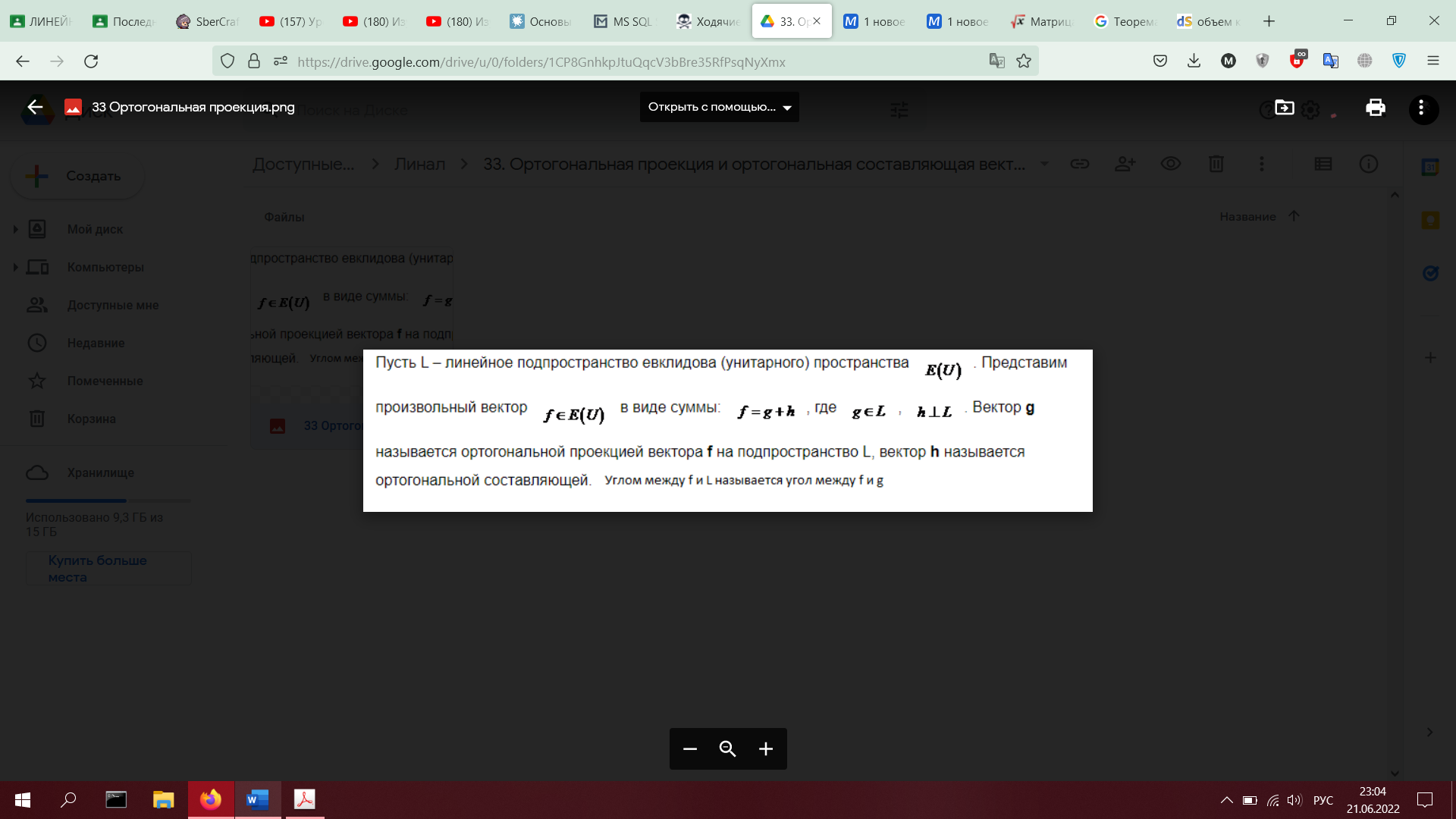
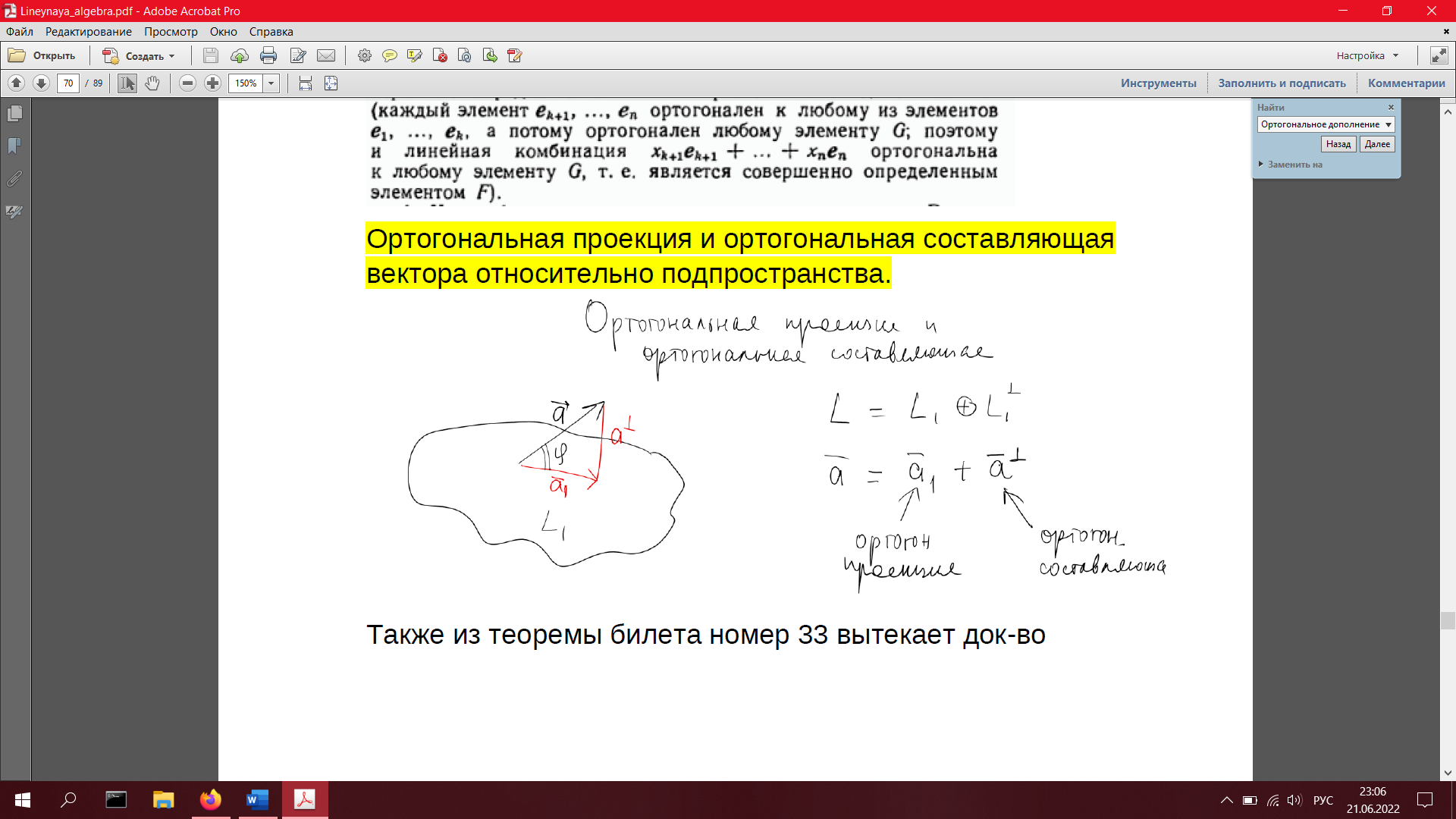
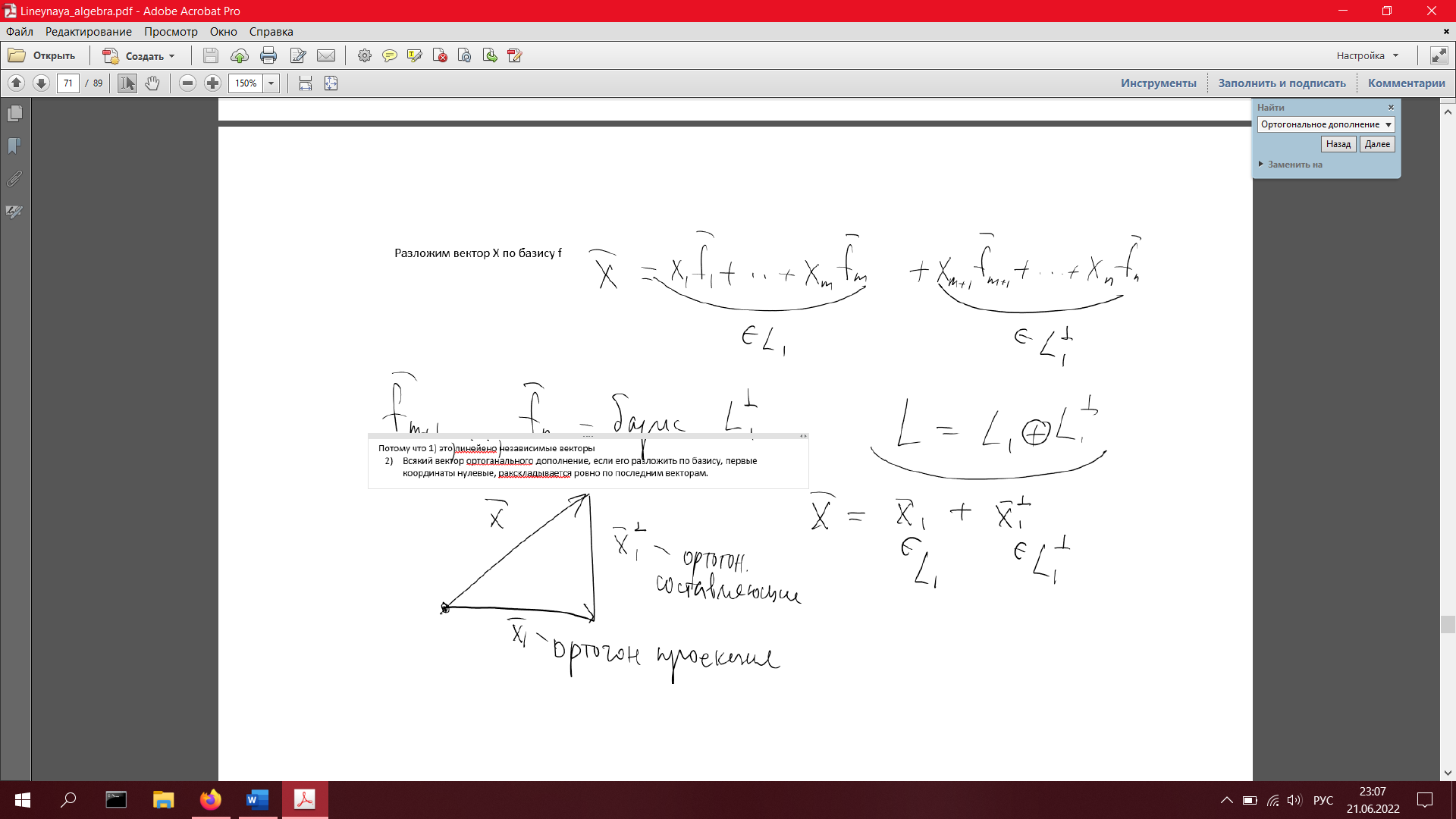
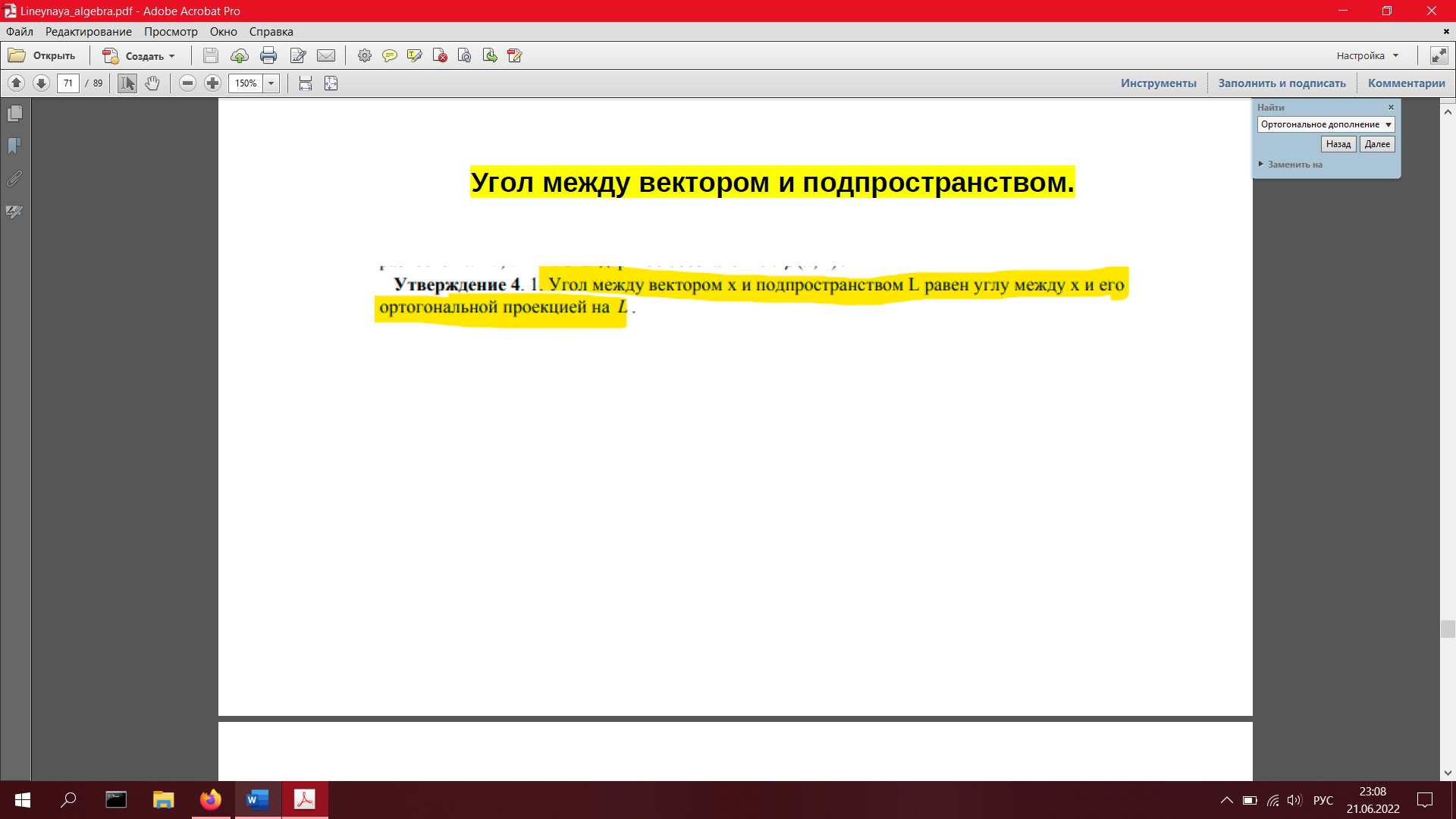
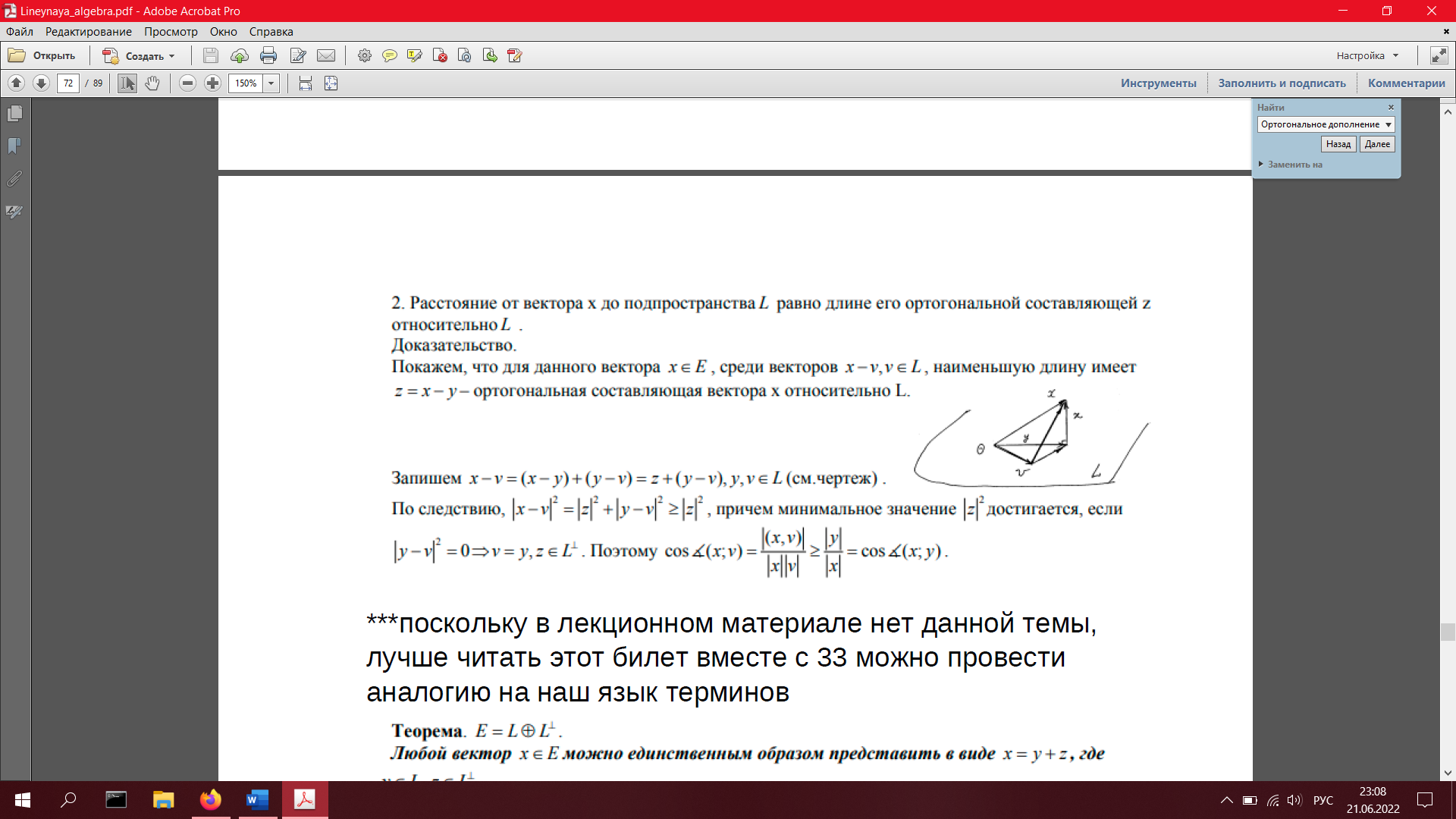
33. Ортогональная проекция и ортогональная составляющая вектора относительно подпространства. Угол между вектором и подпространством (определения)

ИЛИ

34. Сопряженный оператор. Матрица сопряженного оператора в ортонормированном базисе (с доказательством)

35. Самосопряженный оператор (Эрмитов). Основные свойства: вещественность собственных значений, ортогональность собственных векторов, соответствующих разным собственным значениям, существование ортонормированного базиса из собственных векторов (уметь доказывать все свойства, кроме теоремы о существовании ортонормированного базиса).

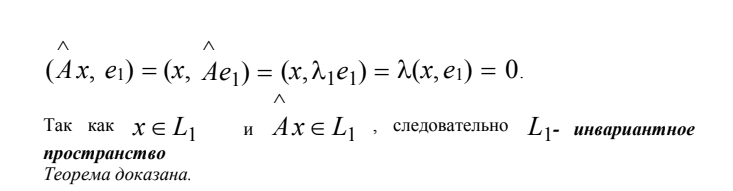
36. Ортогональный оператор. Сохранение длин и углов, геометрический смысл. Ортогональная матрица и её свойства. Ортогональный оператор в 2-мерном случае и теорема об общем виде ортогонального оператора (уметь доказывать все свойства, кроме теоремы об общем виде)

Таким образом, ортогональный оператор сохраняет скалярное произведение, а значит, он сохраняет длины векторов и углы между ними. 

геометрический смысл ортогонального оператора в R¹и R².

В случае пространства R¹ базисный вектор е ортогональным оператором A переводится в вектор Aе   R¹. Следовательно, Aе = lе, где l =   (свойство 4°), т. е. Aе =   е. А это означает, что A – либо тождественный оператор (Aе = е), либо центральная симметрия (Aе = – е).

Ортогональный оператор в 2-мерном случае ???

теорема об общем виде ортогонального оператора- ???

37. Квадратичные формы. Изменение матрицы формы при замене базиса (доказать).

38. Приведение квадратичной формы к каноническому виду методом Лагранжа(на пр имере)

39. Нормальный вид квадратичной формы. Закон инерции квадратичных форм.

40. Теорема о приведении квадратичной формы к каноническому виду с помощью ортогонального преобразования.

41. Знакоопределенные квадратичные формы. Критерий Сильвестра (без доказательства)

ИЛИ