
171101
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”
ОБЧИСЛЕННЯ ПОЛІНОМІВ ЛЕЖАНДРА РІЗНИМИ МЕТОДАМИ
МЕТОДИЧНІ ВКАЗІВКИ
до лабораторної роботи з курсу “Основи фізичної геодезії”
для студентів геодезичних спеціальностей
Затверджено на засіданні кафедри
вищої геодезії та астрономії. Протокол № 10 від 15.05.2017 р.
Львів – 2017
Обчислення поліномів Лежандра різними методами : метод. вказівки до лабораторної роботи з курсу “Основи фізичної геодезії” для студентів геодезичних спеціальностей / уклад.: Б. Б. Джуман, О. М. Марченко. – Львів : Видавництво Львівської політехніки, 2017. – 8 с.
Укладачі |
Джуман Б. Б., канд. техн. наук, асист., |
|
Марченко О. М., д-р фіз.-мат. наук, проф. |
Відповідальний за випуск Заблоцький Ф. Д., д-р техн. наук, проф.
Рецензент |
Зазуляк П. М., д-р фіз.-мат. наук, проф. |
2

ЗАГАЛЬНІ ПОЛОЖЕННЯ
У різних задачах фізичної геодезії, особливо для дослідження гравітаційного поля Землі, використовують поліноми Лежандра. Вони формують повну систему функцій і їх можна визначити як розв’язок диференційного рівняння Лежандра другого порядку [1]
(1- x2 ) × P'' (x) - 2x × P' (x) + n(n +1) × P (x) = 0, |
(1) |
||
n |
n |
n |
|
де Pn (x) – поліном Лежандра n-го порядку, а змінна x має область визначення [−1;+1]. Для спрощення приймемо, що n завжди ціле невід’ємне, тому збігається з індексом полінома. Для прикладних задач фізичної геодезії доволі зручно ввести заміну x = cosθ , що пов’язано з використанням сферичної системи координат. У такому випадку рівняння (1) матиме такий вигляд:
sin2 q× P'' (cosq) - 2cosq× P' |
(cosq) + n(n +1) × P (cosq) = 0 . |
(2) |
||||||||||||||
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
Ввівши поняття норми поліномів Лежандра |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ò1 Pn2 (x)dx |
|
|
|
|
|
||||
|
Pn |
|
|
|
= |
= |
2 |
|
, |
(3) |
||||||
|
|
|
||||||||||||||
|
|
|
|
|
2n +1 |
|||||||||||
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отримаємо систему функцій |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (x) , |
|
|
|||||||
|
|
|
|
|
(x) = |
|
2n +1 |
|
(4) |
|||||||
|
|
P |
|
|||||||||||||
|
|
|
|
|
n |
|
2 |
|
|
n |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
яка утворюватиме ортонормовану систему функцій на відрізку [-1;+1], тобто
|
+1 |
|
|
|
|
|
|
|
|
ò |
|
|
|
|
(5) |
||
|
Pk (x)Pl (x)dx = dkl , |
|||||||
|
−1 |
|
|
|
|
|||
де δkl |
– символ Кронекера, тобто dkl = |
ì1, |
k = l |
. |
|
|||
í |
k ¹ l |
|
||||||
|
|
|
|
|
î0, |
|
|
|
Також поліноми Лежандра можна отримати зі степеневих поліномів, провівши ортогоналізацію Грамма-Шмідта. Оскільки поліноми Лежандра є поліномами від x степені n, вони мають n нулів. Усі ці нулі є дійсними
і містяться в |
інтервалі −1≤ x ≤ +1, або, відповідно до запису (2), |
0 ≤ θ ≤ π . Отже, |
поліноми Лежандра змінюють свій знак n разів на цьому |
інтервалі [2]. |
|
Вигляд перших семи поліномів Лежандра зображено на рис. 1. Практично поліноми Лежандра можна обчислювати різними способами:
розкладом функції оберненої відстані в ряд Маклорена, гіпергеометричними рядами, рекурентними формулами та іншими.
3
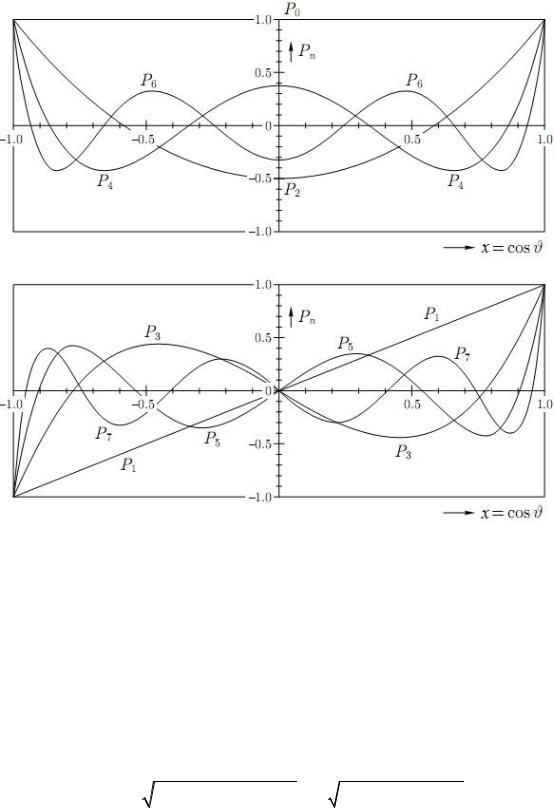
Рис. 1. Поліноми Лежандра як функції x = cosθ : n парне (зверху) і n непарне (знизу)
Обчислення поліномів Лежандра розкладом функції оберненої відстані в ряд Маклорена
Відстань l між двома точками зі сферичними координати P(r,θ,λ) та P′(r′,θ′,λ′) можна задати так:
|
|
|
|
|
|
l2 = r2 + r′2 − 2rr′cosψ , |
|
|
(6) |
||||||||||||
де ψ – кут між радіус-векторами r і r′ |
(рис. 2). Прийнявши |
r′ < r , |
|||||||||||||||||||
справедливою буде рівність |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
= |
|
|
1 |
|
|
= |
|
|
|
|
|
1 |
|
, |
(7) |
|||
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
r2 − 2rr′cosψ + r′2 |
r 1 |
− 2αcosψ + α2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
де α = |
r′ |
. Ввівши функцію f |
(α) = (1− 2αcosψ + α |
2 |
|
− |
1 |
|
|
|
|
||||||||||
) |
2 , перепишемо (7) так |
||||||||||||||||||||
r |
|
|
|||||||||||||||||||
|
|
|
|
|
1 |
= 1 f (α). |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8) |
|||||||
|
|
|
|
|
|
l |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Рис. 2. Просторова відстань l
Розклавши функцію f (α) |
у ряд Маклорена по α , отримаємо формулу |
||||||||||
|
1 |
∞ |
(n) |
(0) |
|
|
1 |
∞ |
|
|
|
1 = |
å |
f |
|
an = |
åPn (cosy)an . |
(9) |
|||||
r |
|
|
|
r |
|||||||
l |
n=0 |
n! |
n=0 |
|
|
||||||
Із формули (9) можна легко отримати вираз для обчислення поліномів |
|||||||||||
Лежандра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (cosy) = |
|
f (n) (0) |
. |
(10) |
||||
|
|
|
|
|
|
||||||
|
|
|
|
n |
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обчислення поліномів Лежандра з використанням гіпергеометричного ряду
Гіпергеометричну функцію F можна представити за допомогою ряду,
який має такий вигляд |
|
|
|
|
|
|
|
|
|
|
|
∞ é k−1 |
(a + l)(b + l) ù |
k |
|
ab z |
|
a(a +1)b(b +1) z2 |
|
||||
F(a,b;c; z) =1+ åêÕ |
|
ú z |
|
=1+ |
|
|
|
+ |
|
|
+ ... (11) |
|
|
c 1! |
c(c +1) |
2! |
|||||||
k=1 ë l=0 |
(1+ l)(c + l) û |
|
|
|
|
||||||
Поліноми Лежандра можна розкласти за допомогою гіпергеометричного |
|||||||||||
ряду як |
|
|
|
|
|
|
|
|
|
|
|
|
P (cosq) = F(-n,n +1;1;1- cosq). |
|
(12) |
||||||||
|
n |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обчислення поліномів Лежандра з використанням рекурентної формули
Рекурентною називається формула, яка дозволяє обчислити наступні члени числової послідовності через знання попередніх членів. У випадку
поліномів Лежандра рекурентна формула має такий вигляд |
|
||||||
P |
(x) = |
2n +1 xP (x) - |
n |
P |
(x) . |
(13) |
|
|
|||||||
n+1 |
|
n +1 |
n |
n +1 n−1 |
|
|
|
|
|
|
5 |
|
|
|
|
Очевидно, формула (13) справедлива тільки у випадку, якщо n ³1. Для знаходження чергового полінома Лежандра за рекурентною формулою необхідно мати значення двох попередніх поліномів.
Приклад обчислень поліномів Лежандра
Вхідні дані : q = 28° .
Обчислимо P0 (x) з використанням формули (10). Оскільки нульова похідна
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
від функції рівна самій |
функції, отримаємо |
|
f (0) (a) = (1- 2acosy + a2 )− |
|
. |
|||||||||||||||||
|
2 |
|||||||||||||||||||||
Значення цієї функції при α = 0 буде |
f (0) (0) = (1- 2 ×0 ×cosy + 02 )− |
1 |
=1, своєю |
|||||||||||||||||||
2 |
||||||||||||||||||||||
чергою, 0!=1. Остаточно отримаємо P (x) = |
|
f |
(0) (0) |
=1. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
|
|
|
|
0! |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Знайдемо вираз P1(x), використовуючи формули (11) та (12). Оскільки в |
||||||||||||||||||||||
такому випадку n =1, отримаємо |
|
|
|
1- x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
P (x) = F(-1,2;1; |
) . |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
За формулою (11) знайдемо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1− x |
|
|
|
|
|
|
|||||||
|
|
|
1- x |
|
|
-1× 2 |
|
|
|
|
|
|
||||||||||
F(-1,2;1; |
) =1 |
+ |
2 |
|
|
|
= x , |
|
|
|
|
|||||||||||
2 |
1 |
|
|
|
|
1! |
|
|
|
|
|
|
||||||||||
тобто P1(x) = x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знайдемо вираз P2 (x) |
за рекурентною формулою. У такому випадку |
|||||||||||||||||||||
n =1. Взявши за основу формулу (13), |
отримаємо |
|
|
|
|
|
|
|
|
|||||||||||||
P |
(x) = |
2 ×1+1 xP (x) - |
|
|
1 |
|
|
P |
|
(x) . |
|
|
|
|
||||||||
1 |
+1 |
|
|
|
|
|
||||||||||||||||
1+1 |
|
|
1+1 |
1 |
|
|
|
|
1−1 |
|
|
|
|
|
||||||||
Знаючи значення P0 (x) і P1(x), після незначних математичних перетворень
P2 (x) = 12 (3x2 -1) .
Знайдемо значення перших трьох поліномів Лежандра в точці θ = 28° .
P0 (cos25°) = 1;
P1(cos25°) = cos25° = 0.883;
P2 (cos25°) = 12 (3cos2 25° -1) =0.669.
6
ЛІТЕРАТУРА
1.Марченко О. М. Дослідження гравітаційного поля, топографії океану та рухів земної кори в регіоні Антарктики : монографія / О. М. Марченко, К. Р. Третяк, А. Я. Кульчицький, Ю. І. Голубінка, Д. О. Марченко, Н. П. Третяк. – Львів: Видавництво Львівської політехніки, 2012. – 308 с.
2.Джуман Б. Б. Про побудову моделі локального гравітаційного поля /
Б. Б. Джуман. – Геодинаміка. – № 1(14), 2013. – C. 29–33.
Вхідні дані
Варіант № |
θ,° |
Варіант № |
θ,° |
Варіант № |
θ,° |
1 |
5 |
11 |
55 |
21 |
105 |
2 |
10 |
12 |
60 |
22 |
110 |
3 |
15 |
13 |
65 |
23 |
115 |
4 |
20 |
14 |
70 |
24 |
120 |
5 |
25 |
15 |
75 |
25 |
125 |
6 |
30 |
16 |
80 |
26 |
130 |
7 |
35 |
17 |
85 |
27 |
135 |
8 |
40 |
18 |
90 |
28 |
140 |
9 |
45 |
19 |
95 |
29 |
145 |
10 |
50 |
20 |
100 |
30 |
150 |
7
НАВЧАЛЬНЕ ВИДАННЯ
ОБЧИСЛЕННЯ ПОЛІНОМІВ ЛЕЖАНДРА РІЗНИМИ МЕТОДАМИ
МЕТОДИЧНІ ВКАЗІВКИ
до лабораторної роботи з курсу “Основи фізичної геодезії”
для студентів геодезичних спеціальностей
Укладачі |
Джуман Богдан Богданович |
|
Марченко Олександр Михайлович |
Редактор |
Анна Весній |
Комп’ютерне верстання |
Марти Гарасимів |
Здано у видавництво 29.06.17. Підписано до друку 04.08.2017. Формат 60×84 1/16. Папір офсетний. Друк на різографі.
Умовн. друк. арк. 0,65. Обл.-вид. арк. 0,4. Наклад 30 прим. Зам. 171101.
Видавець і виготівник: Видавництво Львівської політехніки
Свідоцтво суб’єкта видавничої справи ДК № 4459 від 27.12.2012 р.
вул. Ф. Колесси, 4, Львів, 79013
тел. +380 32 2582146, факс +380 32 2582136 vlp.com.ua, ел. пошта: vmr@vlp.com.ua
8
ОБЧИСЛЕННЯ ПОЛІНОМІВ ЛЕЖАНДРА РІЗНИМИ МЕТОДАМИ
МЕТОДИЧНІ ВКАЗІВКИ
до лабораторної роботи з курсу “Основи фізичної геодезії”
для студентів геодезичних спеціальностей
9
