Добавил:

Justeeeek100500 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

Супутникова геодезія

Файл:

Усе

.pdf

Скачиваний:

Добавлен:

28.06.2022

Размер:

13.73 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 2414 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

16
2.7.1. Лінійна модель для визначення відносного	місцеположення.

Існує багато методів вирівнювання результатів вимірювань. Але тут розглянуто лише параметричне МНК-вирівнювання (вирівнювання за методом найменших квадратів). Воно базується на рівняннях, в яких спостереження подаються у вигляді функції невідомих параметрів. У випадку нелінійних рівнянь звичайно здійснюється розвинення в ряд Тейлора. Це вимагає знання наближених

								(2.76)

			I Ax				,

де I – вектор спостережень, A – твірна матриця,									– вектор невідомих параметрів.
де I – вектор спостережень, A – твірна матриця,								x	– вектор невідомих параметрів.
	Якщо ввести додаткові позначення: 02
	Якщо ввести додаткові позначення: 02						–	апріорна варіація, – коваріаційна
матриця, тоді матриця спостережень
				1
		Q1		1		,		(2.77)
		Q1		02		,		(2.77)
				02
а
					1
		P Q			1			(2.78)
1

є матрицею ваг. Припущення, що кількість спостережень дорівнює п, а невідомих – и, веде до твірної матриці A з п рядками та и стовпчиками. Для n > u система (2.74) перевизначена і взагалі взаємно неузгоджена через похибки спостережень чи шум. Для забезпечення узгодженості до вектора спостережень додається вектор шумів n , і тому рівняння (2.74) перетворюється в наступне:

(2.79)

Розв’зання цього рівняння стає однозначним за допомогою принципу

найменших квадратів

min .

Застосування цього принципу

приводить до

системи нормальних рівнянь

A T P I ,

(2.80)

розв’язок якої

PI ,

(2.81)

можна подати у спрощеному вигляді:

(2.82)

де

PA і

AT PI .

Матрицю Qx

отримаємо за

допомогою закону перетворення

коваріацій із

співвідношення

PI у вигляді

T ,

(2.83)

який шляхом зміни

1 зводиться до

1 .

(2.84)

У випадку визначення відносного місцеположення розглядаються лише фази несучих хвиль. Тому зрозуміло, як потрібно перейти від більш широкої моделі фаз до моделі коду. Крім того, лінеаризація та складання системи лінійних рівнянь залишаються по суті однаковими для фаз та їх комбінацій. Вони можуть бути виконані за аналогією для кожної з моделей. Тому для детального розгляду вибрані подвійні різниці. Модель для подвійних різниць у рівнянні (2.13), помножена на , записується у вигляді

ABjk (t) ABjk (t) N ABjk ,

(2.85)

де член ABjk , що відображає геометрію, визначається за формулою

ABjk (t) kB (t) Bj (t) kA (t) Aj (t) .

(2.86)

З цієї формули випливає, що для утворення подвійної різниці необхідно чотири спостереження. Кожен з чотирьох членів повинен бути лінеаризований, що веде до формули

jk (t) k

(t)

X k (t) X B0

Y k (t) YB0

kB0 (t)

Z k

(t) Z B0

Z B

Z Bk

0 (t)

X j (t) X

Y j (t) Y

(t)

Bj 0 (t)

Z j (t) Z B0

Z B

Bj 0 (t)

(t)

X k (t) X A0

X A

Y k (t) YA0

kA0 (t)

(2.87)

Z k (t) Z A0

Z A

kA0 (t)

(t)

X j (t) X A0

X A

Y j (t) YA0

Aj 0 (t)

Z j (t) Z A0

Z A .

Aj 0 (t)

Для того щоб отримати лінійну систему у вигляді I Ax , слід ввести наступні скорочення:

X k (t) X A0

X j

(t) X A0

a XA (t)

kA0 (t)

Aj 0 (t)

Y k (t) YA0

Y j (t) YA0

aYA (t)

kA0 (t)

Aj 0 (t)

Z k (t) Z A0

Z j (t) Z A0

aZA (t)

kA0 (t)

Aj 0 (t)

X k (t) X B0

X j

(t) X B0

a XB (t)

kB0 (t)

Bj 0 (t)

aYBjk (t)

Y k (t) Y

Y j (t) Y

kB0 (t)

Bj 0 (t)

Z k (t) Z B0

Z j (t) Z B0

aZB (t)

kB0 (t)

Bj 0 (t)

а для лівої частини – позначення

l ABjk (t) ABjk (t) kB0 (t) Bj 0 (t) kA0 (t) Aj 0 (t) ,

(2.88)

(2.89)

яке містить виміри, і всі члени, обчислені з наближених значень. Використовуючи скорочення (2.88) та (2.89), запишемо лінійне рівняння спостережень у вигляді

l ABjk (t) a XAjk (t) X A aYAjk (t) YA aZAjk (t) Z A										(2.90)
a jk			a jk		a jk			N jk	,	(2.90)
a jk	(t) X	B	a jk	(t) Y	a jk	(t) Z	B	N jk	(t) ,
XB		B	YB	B	ZB		B	AB

яке відображає загальний випадок двох невідомих точок бази. Однак координати однієї точки (наприклад А) повинні бути відомі у випадку визначення відносного місцеполження. Відома точка А скорочує кількість невідомих параметрів на три, оскільки має місце співвідношення

X A YA Z A 0 ,

(2.91)

що введена до невеликої зміни члена у лівій частині:

l ABjk (t) ABjk (t) kB0 (t) Bj 0 (t) kA (t) Aj (t) . (2.92)

Припускаючи тепер стеження за чотирма супутниками j, k, l, m у дві епохи t1, t2, отримаємо матрично-векторну систему рівнянь:

l ABjk

X B

a XBjk

aYBjk t1

aZBjk t1

aYBjl t1

aZBjl t1

l ABjl

a XBjl

l ABjm

a XBjm

aYBjm t1

aZBjm t1

Z B

aYBjk t2

aZBjk t2

(2.93)

l ABjk

N AB

a XBjk

aYBjl t2

aZBjl t2 0

l ABjl

N AB

a XBjl

N jm

l AB

a XB

aYB t2

aZB t2 0

яку можна розв’язати. Слід зазначити, що для однієї епохи ця система має більше невідомих параметрів ніж рівнянь.

2.7.3.Оцінка точності.
Виходячи з рівняння вимірів (2.90), рівняння похибок у вигляді:
Ax l n	(2.94)

де п - вектор похибок розмірності (n,1), який представимо так:

	v1

	v2	,
n	v2		(2.95)
n	...		(2.95)
	...

	vn

де v1, v2, ..., vn - похибки.

Середня квадратична похибка одиниці ваги запишеться у наступному вигляді

	nn T
	n k ,	(2.96)

де п - кількість вимірів, k - кількість невідомих.

Тоді рівняння для похибок координат (враховуючи (2.84)) приймуть вигляд mx Q11 ,


my Q22 ,			(2.97)

mz Q33 .

Похибка визначення місцеположення пункту обчислимо за формулою


M m2		m2	m2 .	(2.97)
	x	y	z

Важливим фактором для досягнення високоточних результатів, особливо у визначенні місцеположення окремої точки та в кінематичній геодезичній зйомці, є геометрія видимих супутників. Через відносний рух супутниківця геометрія змінюється в часі. Мірою геометрії є коефіцієнт зменшення точності (DOP). Нижче наведений перелік параметрів DOP.

GDOP – зменшення точності, обумовлене геометрією;

РDOP – зменшення точності визначення координат;

TDOP – зменшення точності визначення часу;

HDOP – зменшення точності планових координат;

VDOP – зменшення точності визначення вертикальної (зенітної) компоненти координат.

Вище наведені параметри можна означити за наступними формулами:

GDOP 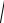qxx q yy qzz qtt ,

PDOP 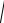qxx q yy qzz ,


TDOP qtt ,			(2.98)

HDOP qxx q yy ,

GDOP qhh ,

де qii – компоненти оберненої нормальної матриці рівнянь спостережень. Її можна представити у вигляді

				T		1
	Qx		A	T	A	1	,	(2.99)

або

					q xx

					q xy
	Qx				q xy
	Qx				q xz

					q xt

q xy	q xz
q yy	q yz
q yz	qzz
q yt	qzt

q xt

q yt	,	(2.100)
qzt	,	(2.100)
qzt

qtt

2.8. Корелатний спосіб урівнювання.

В трьох умовних рівняння урівняних фігур

v1x v2 x v3x wx 0,
v1y v2 y v3y wy 0,	(2.101)
v1z v2z v3z wz 0,
похибки визначення приростів координат пунктів позначені через	v1i ,v2i ,v3i , wi –

нев’язки, де і може приймати значення x, y, z . Це саме рівняння можна також записати в матричному вигляді


			BV W 0 ,																					(2.102)
де матриця
	1	1	1		0						0				0			0		0		0


B 0		0	0		1						1				1			0		0		0	,	(2.103)
	0	0	0		0						0				0			1		1		1

а вектори
			v1x														wx
				v2 x													wx


	V									,			W			wx					.			(2.103)
	V				...					,			W			wx					.			(2.103)
					...

																	wx
			v3z
Вводячи діагональну матрицю обернених ваг вимірів
			1

			P
					1					1
										1
	P 1
	P 1								P												,			(2.104)
											2
															...
															...
																		1

																			P
																			P
																			n
нормальне рівняння отримаємо у вигляді

							NK w 0 ,																	(2.105)
де матриця

						N						BP 1B T ,												(2.106)
а вектор корелат
														k1

														k2
								K						k2				,						(2.106)
								K							...			,						(2.106)
															...

														kr

Отримавши із розв’язку (2.104) вектор корелат (розв’язування можна проводити у вигляді K N 1W ), отримаємо

pV 2 kW .

Похибка (чи m при рівноточних вимірах), вичисляється за формулою


V		T PV	,
	n k		,
	n k

а середні квадратичні похибки визначення приростів координат m x N11 ,

m x N22 , m x N33 .

(2.107)

(2.108)

(2.109)

Незбурений рух ШСЗ

Диференціальні рівняння незбуреного руху

Використання штучних супутників Землі (ШСЗ) (з 4 жовтня 1957 року) для наукових і науково-технічних задач геодезії стало початком створення космічної геодезії. Космічна геодезія дає можливість в короткі терміни і з більшою точністю, ніж традиційні методи, розв’язувати задачі геодезії.

Якщо розглядати методи космічної геодезії в послідовності їх розвитку, то першим вважається геометричний метод, суть якого у синхронному фотографуванні ШСЗ на фоні зоряного неба мінімум із двох пунктів на поверхні Землі. Така організація спостережень дозволяє визначити напрям вектора, що з’єднує ці пункти. Множина таких векторів утворює векторну просторову мережу

– космічну тріангуляцію. Наступний, найбільш загальний метод – динамічний,

який базується на вивченні еволюції орбіти ШСЗ в часі для визначення динамічних параметрів, якими є параметри гравітаційного поля Землі

(геопотенціалу). При цьому одночасно визначаються координати пунктів спостереження у єдиній геоцентричній системі координат (земній або гринвіцькій). В орбітальному методі за допомогою вимірів, зроблених на наземних пунктах чи безпосередньо із супутника, визначаються координати пунктів і елементи орбіти супутника.

Рух супутника в просторі визначається такими факторами: притяганням гравітаційних полів Землі, Місяця, Сонця та інших планет Сонячної системи,

місячно-сонячними припливами, тиском сонячного світла, гальмуванням в атмосфері, дією магнітного поля Землі та іншими. З перелічених факторів вплив гравітаційного поля Землі є домінуючим, тому у першому наближенні,

розглядаючи рух ШСЗ, дією інших факторів можна знехтувати.

Якщо ж прийняти, що тіло Землі має сферичну форму з рівномірним розподілом масс в сереюдині, то у цьому випадку притягання Землі відповідає притяганню матеріальної точки, масса якої дорівнює масі Землі. Рух супутника

довкола такої планети, при відсутності інших факторів, відбувається за законами Кеплера, і його називають незбуреним або кеплеровим.

Нехай маємо геоцентричну інерціальну систему координат: початок – у

центрі масс Землі, вісь Oz співпадає із середньою віссю обертання Землі у просторі, вісь Ox – у напрямку середньої точки весняного рівнодення , вісь Oy –

лежить у площині середнього екватора на 90 на схід від осі Ox. Нагадаємо, що точка весняного рівнодення є точкою перетину небесного меридіана з екліптикою. Екліптика – це видимий річний рух Сонця по небесній сфері, тобто це приблизно осереднена орбіта Землі навколо Сонця.

Диференціальні рівняння незбуреного руху ШСЗ на основі законів

ньютонівської механіки. На основі другого закону Ньютона вектор сили F

дорівнює

F m r ,

(1)

де r - вектор прискорення супутника, m – його маса. Модуль сили F згідно із законом всесвітнього тяжіння буде

F	f	M m	,	(2)

		r 2

де f – гравітаційна стала, r – відстань від центра маси Землі M до супутника m.

Вектор сили взаємодії Землі і супутника, виходячи із закону (2), виразиться так:

F f	M m	r	.	(3)
	r 2
		r

Тут r – вектор положення супутника, а його складовими у прийнятій геоцентричній системі - є координати ШСЗ, тобто

x
r y	.	(4)

z

Прирівнюючи праві частини формул (1) і (3), отримаємо диференціальні рівняння незбуреного руху ШСЗ у векторній формі:

r ,

(5)

де fM – гравітаційний параметр

Землі. Диференціальні рівняння

(5) в

координатній формі мають вид

dt2

r 3

d 2 y

(6)

r 3

dt2

r 3

де x , y і z – складові вектора прискорення r супутника. Інтегруванням диференціальних рівнянь руху ШСЗ прогнозується його положення, вектор r

(див. (4)), і складові x , y , z вектора швидкості r на інші моменти часу відносно початкового моменту t0.

Інтегрування диференціальних рівнянь руху. Інтегрування системи трьох рівнянь другого порядку дає наступний загальний розв’язок:

ˆ	ˆ			, c3
x	x t, c1 , c2			, c3
ˆ	ˆ			, c3
y y t, c1 , c2				, c3
zˆ zˆ t, c1 , c2 , c3
zˆ zˆ t, c1 , c2 , c3																	,	(7)
x x t, c , c				, c			, c			, c			, c				,	(7)
x x t, c , c		2		, c	3		, c	4		, c	5		, c		6
	1	2			3			4			5				6
y y t, c , c				, c			, c			, c				, c
y y t, c , c			2	, c		3	, c		4	, c		5		, c		6
	1		2			3			4			5				6
z z t, c1 , c2 , c3 , c4 , c5 , c6

де t – час, с1, с2, с3, с4, с5, с6 – довільні сталі, які визначаються початковими умовами руху. Ними є параметри орбіти ШСЗ x0 , y0 , z0 , x0 , y0 , z0 на початковий момент t0.

Інтегрування диференціальних рівнянь(5) або (6) виконують різними способами [ ].

Інтеграли площ. Якщо рівняння руху (5) помножити векторно на r,

отримаємо

				r r 0 .	(8)
r r r3				r r 0 .	(8)

Це рівняння тотожне наступному:
	d		0 .

	dt	r r			(9)
Інтегруючи рівняння (9) отримаємо
		r r c ,			(10)

де стала інтегрування с є інтегралом площ у векторній формі. Векторний добуток

(10) у матричній формі має такий вид:

i	j	k
						,	(11)
x	y	z	ic1	jc2	kc3	,	(11)
x	y	z

де с1, с2, с3 – складові вектора с, а i, j, k – одиничні вектори – орти відповідних осей координат. Викреслюючи перший рядок матриці в (11) і стовпчик відповідного орта, отримаємо визначники другого порядку, обчислюючи котрі,

маємо три інтеграли площ в координатній формі

yz zy c1 , zx xz c2 , xy yx c3 . (12)

Назва інтеграла площ походить від сутності векторного добутку,

результатом котрого є вектор с, модуль якого дорівнює площі паралелограма зі

сторонами r і r . Напрям вектора с перпендикулярний до площини, в якій

лежать вектори r і r .

Інтеграл енергії. Векторне диференціальне рівняння незбуреного руху (5)

помножимо скалярно на 2r , маємо
2r r	2	r r .	(13)

	r 3

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 2414 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете Супутникова геодезія

#
28.06.2022823.32 Кб5Методичні рекомендації. Прогнозування спостережень ШСЗ.pdf
#
28.06.2022871.53 Кб5Методичні рекомендації. Форма орбіти та рух ШСЗ за законами Кеплера.pdf
#
28.06.20222.25 Mб9Питання на екзамен.pdf
#
28.06.2022448.42 Кб4Системи координат і шкали часу.pdf
#
28.06.20222.4 Mб13Сферична астрономія.pdf
#
28.06.202213.73 Mб7Усе.pdf
#
28.06.2022762.57 Кб9Шумаков Ф.Т. Супутникова геодезія.-Харків ХНАМГ, 2009.- 88 с..pdf