Добавил:

Way_J Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Уравнения математической физики. Методы математической физики.

Файл:

Методы математической физки Меркулов

.pdf

Скачиваний:

130

Добавлен:

28.05.2022

Размер:

865.91 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 173 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

kykk2

cos(2 k) 1

sin(2 k)

Первые 3 коэффициента

= 0

194988,

0:711385

= +

= 0 128501.

Будем искать решение (1.16)

ckyk(x). Учитывая, что

в виде v(x) =

+1 +1

L(v) = ckL(yk) = ck kyk;

k=1 k=1

получаем

ck kyk(x) = gkyk(x):

			k=1		k=1
Отсюда
ck =	gk	=	1	(4 + k2)	cos(2 k) 1	+	sin(2 k)	:
ck =		=	( 2 + 3) (5 + k2)		k2	+		:
	k		( 2 + 3) (5 + k2)		k2		k
Первые 3 коэффициента ряда будут
c1 = 0:057353;				c2 = 0:103529; c3 = 0:008797:
Окончательно решение задачи (1.16) примет вид

v(x) = ck cos( k(3 x))

k=1

и решение исходной задачи

u(x) = ck cos( k(3 x)) + x 4:

k=1

В качестве приближенного решения задачи можно взять частичную сумму ряда Фурье

uN (x) = ck cos( k(3 x)) + x 4:

k=1

В табл. 1.1 приведены значения приближенного решения u3(x). Для сравнения приводятся значения точного решения

e p

(

) = 0

001019

1 516849

Таблица 1.1

1.0

1.5

2.0

2.5

3.0

u3(x)

2:937097

2:428362

2:014745

1:613016

1:152085

u(x)

2:929269

2:432516

2:014917

1:609222

1:157683

Получить точное решение исходной задачи читателю предлагается самостоятельно.

1.5. Уравнение Бесселя. Функция Бесселя

Уравнением Бесселя порядка p (где p 0 – заданное число) называется следующее дифференциальное уравнение:

1		(xy0)0	+ 1	p2	y = 0:
	x			x2
Умножив уравнение на x2, получим
	x(xy0)0		+ (x2 p2)y = 0:			(1.19)

Уравнение (1.19) – линейное однородное дифференциальное уравнение второго порядка. Его общее решение состоит из двух линейно независимых функций. Будем искать решение уравнения (1.19) в виде обобщенного степенного ряда

+1
y(x) = x Xakxk = a0x + a1x +1 + ::: :	(1.20)

k=0

Здесь a0 – первый ненулевой коэффициент ряда. Почленно дифференцируя ряд (1.20), найдем y0. Затем, умножив на x и снова продифференцировав, получим

x(xy0)0 = a0 2x + a1( + 1)2x +1 + a2( + 2)2x +2 + :::

+ ak( + k)2x +k + ::: :

Подставив выражения для x(xy0)0 и для y в уравнение (1.19), получим a0 2x + a1( + 1)2x +1 + a2( + 2)2x +2 + ::: + ak( + k)2x +k + :::

+a0x +2 + ::: + ak 2x +k + :::

p2a0x p2a1x +1 p2a2x +2 ::: p2akx +k ::: = 0:

Приравняв нулю сумму коэффициентов при каждой степени x, составим бесконечную систему уравнений для определения коэффициентов

>a0( 2 p2) = 0;

>a1[( + 1)2 p2] = 0;

>a [( + 2)2 p2] + a = 0;

> 2 0

a3[( + 3)2 p2] + a1 = 0;					(1.21)
>a. k.	[(. . . .+. .k. .).2	. . .	p. .2.].+. .a.k.	. .2.=. . .0.;
>		. . .

:. . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Из первого уравнения получаем 2 p2 = 0 (так как a0 6= 0), следовательно,= p. Пусть = p. Перепишем систему, преобразовав выражения в квадратных скобках:

>>a1(2p + 1) = 0;

>a 2(2p + 2) + a = 0;

> 2 0

<a33(2p + 3) + a1 = 0;

>. . . . . . . . . . . . . . . . . . . . . . . .

>akk(2p + k) + ak 2 = 0;

:. . . . . . . . . . . . . . . . . . . . . . . .

Отсюда видно,что a1 = 0 и все коэффициенты с нечетными номерами равны 0. Коэффициенты ak с четными номерами будут выражаться через a0. Поскольку решение линейного уравнения определяется с точностью до постоянного множителя, значение a0 можно положить произвольным. Пусть

a0 = 2p (p + 1), где (p + 1) – гамма-функция. Тогда

a2n

2(2p + 2)

2(2p + 2)2p (p + 1)

2 2p(p + 1) (p + 1)

;

2p+2 (p + 2)

;

2 22(p + 2)2p+2 (p + 2)

4(2p + 4)

2n 2p+4 (p + 3)

a2n 2

( 1)

2n(2p + 2n) n22(p + n) n!2p+2n (p + n + 1)

При выводе этих соотношений использовано основное свойство гамма-фун- кции z (z) = (z+1). Все коэффициенты ряда найдены, и можно записать решение уравнения (1.19) в виде

y(x) = +1	( 1)n	x	2n+p	:
n=0 n! (n + p + 1)		2
X

Полученный ряд абсолютно сходится для всех значений x (это легко проверить с помощью признака Даламбера). Сумма этого ряда называется функцией Бесселя порядка p и обозначается Jp(x):

J	(x) = +1	( 1)n	x	2n+p	:	(1.22)
p	n=0 n! (n + p + 1)		2			(1.22)
	X

Если в первом уравнении системы (1.21) положить = p, то аналогичными рассуждениями можно получить представление в виде ряда

sin(p )

функции Бесселя отрицательного порядка. В случае, когда p – не целое число, это представление имеет вид

p	+1	( 1)n	x	2n p	(1.23)
p	n=0 n! (n p + 1)		2		(1.23)
J (x) =	X			:
J (x) =				:

Функции Jp(x) и J p(x) линейно независимы, и, следовательно, общее решение уравнения Бесселя

y(x) = C1Jp(x) + C2J p(x):

В случае, когда p = m – целое число, оказывается, что первые n коэффициентов ряда (1.23) равны нулю и функция Бесселя с целым отрицательным индексом

(x) = +1

( 1)n

2n m = +1

( 1)n

2n m

n=m n! (n m + 1)

n=m n!(n m)!

Сделав замену индекса суммирования k = n m, получим

(x) = +1

( 1)k+m

2k+m =

k=0 (k + m)!k!

= ( 1)m +1

( 1)k

2k+m = ( 1)mJ

(x);

k=0 (k + m + 1)k! 2

т. е. функции Jm(x) и J m(x) оказались линейно зависимы и, следовательно, не образуют фундаментальную систему решений уравнения (1.19). Можно доказать, что линейно независимую пару решений составляют функции Jp(x) и Np(x), где функция Np(x), называемая функцией Неймана, определяется как

Np(x) = cos(p )Jp(x) J p(x) sin(p )

для нецелых значений p и

Nm(x) = lim cos(p )Jp(x) J p(x)

p!m

для целого индекса.

Из формулы (1.23) видно, что первое слагаемое ряда для функции

1		x	p
J p(x) равно			, поэтому при x ! 0 функция J p(x) неогра-
	( p + 1)	2

ниченна. Также неограниченны при x ! 0 функции Np(x) и Nm(x), поэтому ограниченное в нуле решение уравнения Бесселя имеет вид

y(x) = CJp(x):

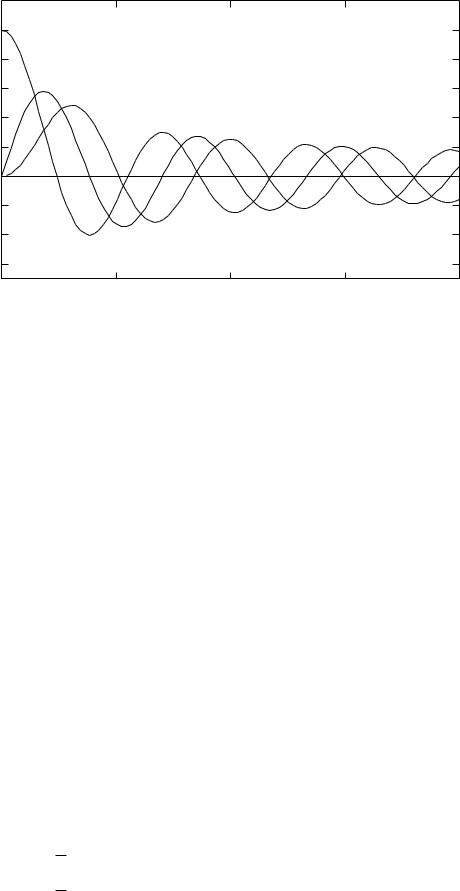
1.2
1	J0(x)
0.8	J1(x)
0.6	J1(x)
0.6	J2(x)
0.4	J2(x)
0.2
0
−0.2
−0.4
−0.6
0	5	10	15	20
		Рис. 1.2

На рис. 1.2 приведены графики функции J0(x), J1(x) и J2(x) [5]. Справедливо [6] следующее асимптотическое представление:

Jp(x) = r		2x		cos	x 2	4		+ O	x3=2		; x ! +1:
					p				1

Отсюда следует, что при больших x график Jp(x) имеет колебательный характер с амплитудой, стремящейся к нулю.

Обозначим через k, k, k соответственно положительные корни уравнений

Jp(x) = 0; Jp0(x) = 0; xJp0(x) + SJp(x) = 0 (S > 0):

Справедливы следующие утверждения [6]:

1) k = k + p 2		4	+ o	k , k ! +1;
				1

2)k, k, k – простые корни;

3)k < k < k:

Используя представление функций Бесселя в виде ряда (1.22), можно получить следующие тождества, связывающие функции Бесселя с разными индексами и их производные:

1)(xpJp(x))0 = xpJp 1(x);

2)(x pJp(x))0 = x pJp+1(x);

3)Jp 1(x) = xp Jp(x) + Jp0(x);

4)Jp+1(x) = xp Jp(x) Jp0(x);

p 1

(x)

p+1

(x) = 2J0(x)

;

6) Jp 1(x) + Jp+1(x) =

Jp(x).

Докажем первое тождество. Из (1.22) получим

xpJp(x) =

2n+2p

( 1)

x 2n+p :

n=0

n! (n + p + 1) 2

Продифференцируем ряд почленно:

( 1)n(2n + 2p)x2n+2p 1

(xpJp(x))0 =

2n+p

n=0

n! (n + p + 1)2

Так как (n + p + 1) = (n + p) (n + p), получим

( 1)nx2n+2p 1

(xpJp(x))0 =

n=0 n! (n + p)22n+p 1

( 1)nx2n+p 1

2n+p

1 = xpJp 1(x):

= xp

n! (n + (p

1) + 1)2

n=0

Доказательство остальных тождеств рекомендуем читателю в качестве самостоятельного упражнения.

1.6.Задача на собственные значения для оператора Бесселя

Оператором Бесселя называется дифференциальный оператор вида

Bp(y) = 1(xy0)0 + p2 y: x x2

В качестве области определения оператора D(B) возьмем множество дважды дифференцируемых функций, заданных на промежутке [0; T ] и удовлетворяющих однородным краевым условиям:

y(x) ограничена при x ! 0 + 0; Ry0(T ) + Sy(T ) = 0;

где R, S – некоторые постоянные, R 0, S 0, jRj + jSj =6 0. Рассмотрим для оператора Bp(y) задачу на собственные значения

1			p2
8		(xy0)0 +		y = y; 0 < x < T;
8	x	(xy0)0 +	x2	y = y; 0 < x < T;
>					!
>		(T ) + Sy(T ) = 0;
>Ry0		(T ) + Sy(T ) = 0;
<
>y(x) ограничена при x					0 + 0;	(1.24)

:p 0; R; S 0 (p = 0; S > 0):

Можно показать, что собственные числа этой задачи положительны. Перепишем уравнение задачи (1.24) в виде

1	(xy0)0	+	p2	y = 0	(1.25)
x			x2

и сделаем замену переменной t = x. Тогда справедлива цепочка ра-

венств y(x) = y

= '(t) = '(p

x). Используя правило дифферен-

цирования сложной функции

= p

; преобразуем уравнение

dt dx

(1.25) к виду

1 d

+ 1

' = 0:

Полученное уравнение – это уравнение Бесселя. Его ограниченным

решением будет '(t) = Jp(t), или, возвращаясь к переменной x, y(x) =

= Jp(p

x). Подставив решение в краевое условие и учитывая, что

dJp(p

Jp0( x);

получим

Обозначим p

Jp0( T ) + SJp(

T ) = 0:

(1.26)

T = и перепишем уравнение (1.26) в виде

R Jp0( ) + ST Jp( ) = 0:

(1.27)

Как известно из 1.5, это уравнение имеет множество простых корнейk, k = 1; 2; ::: . В случае, если R = 0 или S = 0, уравнение (1.27) превраща-

ется в Jp( ) = 0 или Jp0( ) = 0 с аналогичными свойствами. Следовательно, p

будет собственным числом задачи, если T = k. Таким образом, получено множество собственных чисел

k = k 2 ;

где k – корень уравнения (1.27), k = 1; 2; :::; и множество собственных функций

yk(x) = Jp						x +:
				k
			T
n		k			o			1
Система собственных функций Jp				x				1	образует полную ортого-
нальную систему в пространстве L2		T					.	k=1
	[0; T ; x]

Для того чтобы разложить функцию в ряд по системе ортогональных функций Бесселя, потребуется несколько интегральных тождеств.

Утверждение 1.5. Для любых ; 2 R, 6= , выполняется

Jp( )J0

( )

J0( )Jp( )

x x dx = T 2

(1.28)

2 2

Доказательство.

Заметим, что функция y(x) = J

является

решением уравнения с =

, т. е. справедливо равенство

T 2

x Jp

x 0

x = 0:

T 2

Аналогично, если =

, то

T 2

x Jp

x = 0:

T 2

Умножим первое равенство на J

x, а второе – на J

x и вы-

чтем из первого второе:

x Jp

x 0

x x Jp

x +

2 2

x J

x x = 0:

T 2

Проинтегрировав полученное выражение, получим

2 2

x J

x x dx =

T 2

T	0	0			T	x Jp		0	0
	0	0	Jp						0
= Z x Jp T x			Jp	T x dx Z			T x		Jp
0					0

Интегралы в правой части выражения возьмем по частям:

T x dx:

	T
2 2	Z	J			x J		x x dx =
T 2		J			x J		x x dx =
T 2			p	T		p T
	0

= x Jp T x

T x

x Jp T x

T x

0 Jp

T x

x Jp T x

Z x Jp

dx =

T x 0

= Jp0( )Jp( ) Jp0( )Jp( ):

Поделив на 2 2 , получим формулу (1.28).

T 2

Утверждение 1.6. Для любого 6= 0 справедлива формула

T								1		Jp2( ) :
Z	Jp2		T 2	Jp0	( )	2	+		p2		(1.29)
Z	Jp2	T x x dx =	2	Jp0	( )		+		2		(1.29)
0
0

Доказательство. В выражении (1.28) сделаем предельный переход при ! и применим правило Лопиталя:

J ( )J0( )

J0( )J ( )

x dx

T 2 lim

( )J0

( ) + J

( )J00( )

J0( )J0( )

= T 2 lim

( ) 1

Jp( ),

Из уравнения Бесселя (1.19) следует, что Jp00( ) =

Jp0

поэтому

Jp2

T x

dx =

= T 2 lim

Jp( )Jp0( ) Jp( )Jp0( ) 1

Jp( )Jp( ) Jp0( )Jp0( )

T 2

Jp0( )

+ 1

Jp2( ) :

1.7. Оператор Лежандра. Многочлены Лежандра

Оператором Лежандра называется дифференциальный оператор вида

L(y) = (1 x2)y0 0 :

За область определения оператора возьмем функции, дважды дифференцируемые на ( 1; 1). Так как на концах интервала функция p(x) = 1 x2 обращается в нуль, то в качестве однородных краевых условий потребуем ограниченность y(x) при x ! 1.

Поставим для оператора Лежандра задачу на собственные значения

(1 x2)y0

= y;

(1.30)

(y(x)

ограничена при x

Уравнение задачи можно переписать в виде

(x2 1)y00 + 2xy0 y = 0:

(1.31)

Рассмотрим теперь выражения вида

Pn(x) =

(x2 1)n (n) :

2nn!

Достаточно очевидно,

что

Pn(x)

является

многочленом

степени n,

P0(x) 1, P1(x) =

1)0 = x, P2(x) =

(3x

1).

Функции

(x)

называются многочленами

Лежандра.

Утверждение 1.7. Функция Pn(x) является собственной функцией оператора Лежандра, соответствующей собственному числу n = = n(n + 1).

Доказательство. При доказательстве используется формула дифференциального бинома

(uv)(n) = uv(n) + Cn1u0v(n 1) + Cn2u00v(n 2) + ::: + u(n)v:

(1.32)

Здесь Cnk =

n(n 1):::(n k + 1)

– биномиальные коэффициенты.

Запишем очевидное равенство

(x2 1)n 0 = n(x2 1)n 12x:

n + 1

раз

Умножим левую и правую части этого равенства на

продифференцируем:

1)n

0i(n+1) =

n(x2 1)n2x

h(x2 1) (x2

(n+1)

<<< < Предыдущая 1 23 / 173 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете Уравнения математической физики. Методы математической физики.

#
28.05.2022528.91 Кб1Второй типовик.jpg
#
28.05.2022865.91 Кб130Методы математической физки Меркулов.pdf