Учебники 80131

качестве своей подформулы. Пусть СВ получается из СА заменой А в этом вхождении на В. Тогда если A B, то и

СA СB.

Справедливы также следующие утверждения [1, 2].

1. Для каждой формулы можно указать равносильную ей формулу, не содержащую логических символов эквиваленции и импликации.

2. Для каждой формулы существует эквивалентная ей формула с тесными отрицаниями, то есть формула, в которой нет символов , и отрицания стоят при пропозициональных переменных.

Действительно, применяя законы де Моргана, получим:

4.ДВОЙСТВЕННОСТЬ

Вэтом пункте будем рассматривать формулы, содержащие только логические символы , , .

Символы , называются двойственными друг другу. Формула А* называется двойственной формуле А, если она получена из А одновременной заменой всех символов , на двойственные. Очевидно, что (А*)* есть А. Набор значений переменных X1, X2, ... называется двойственным какому-либо набору значений этих же переменных, если он получается из первого набора заменой всех 1 на 0 и 0 на 1.

Пример 4. Рассмотрим две формулы ((X1 X2) X3) 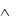X1 и ((X1 X2) X3) X1, двойственные друг другу. Соста-

9

вим для них таблицы истинности.

Таблица 6

Из таблиц истинности видно, что если формула ((X1 X2) X3) X1 принимает значение 1 на каком-либо наборе значений переменных X1, X2, X3, то двойственная формула принимает значение 0 на двойственном к данному набору. Можно показать, что это свойство справедливо и в общем случае.

Важное значение в теории логики высказываний имеет основной принцип двойственности [3, 4]: если А B, то А* B*. Этот принцип обычно применяют для получения новых равносильностей. Например из первого закона де Моргана

10

5. НОРМАЛЬНЫЕ ВИДЫ ФОРМУЛ

Определим теперь некоторые канонические виды формул. Формула называется элементарной конъюнкцией, если она является конъюнкцией, может быть, одночленной, пере-

менных и их отрицаний. Например, формулы X1, X 2 , X1

X 2 , X1 X 2 X3 есть элементарные конъюнкции.

Формула находится в дизъюнктивной нормальной фор-

ме (ДНФ), если она является дизъюнкцией элементарных конъюнкций. Формулы X1, X 2 , (X2 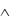X3) X1 , X2 X3,

(X2 X3) ( X1 X4) находятся в дизъюнктивной нормальной

форме.

Справедливо следующее утверждение [1]. Для любой формулы А можно найти такую формулу В, находящуюся в ДНФ, что А В. Для приведения ПФ к ДНФ рекомендуется: исключить операции и с помощью равносильностей 16) и 17); с помощью законов де Моргана привести отрицания к независимым переменным; а затем по дистрибутивному закону раскрыть скобки.

Пример 5. Привести к ДНФ формулу (X1 X2) ( X 2

X3).

Решение. Применяя равносильность 17), получаем:

Таким образом исходная формула приведена к ДНФ. Заметим, что полученная ДНФ не является единственной и, используя закон поглощения, ее можно упростить:

X1 X 2 ( X 2 X3) X1 X 2 .

Формулу называют элементарной дизъюнкцией, если она является дизъюнкцией, возможно, одночленной, переменных и отрицаний переменных. Например, элементарными

дизъюнкциями являются формулы X1, X 2 , X1 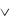X 2 , X1

11

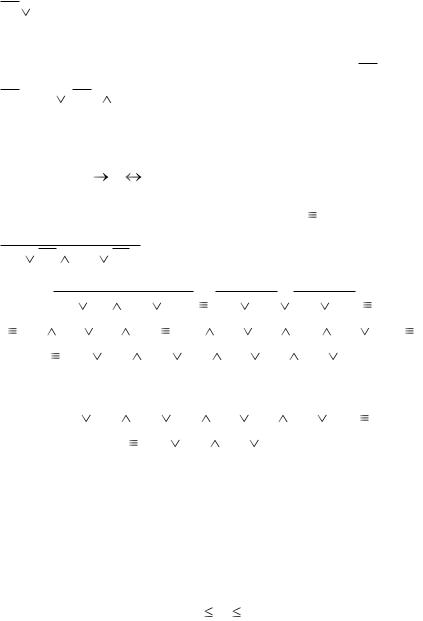
X 2 X3.

Формула находится в конъюнктивной нормальной фор-

ме (КНФ), если она является конъюнкцией, возможно, одночленной, элементарных дизъюнкций. Формулы X1, X 2 , X1

X 2 , (X1 X 2 ) X3 находятся в КНФ.

Используя понятия двойственности, можно дать равносильное определение КНФ. Формула А находится в конъюнктивной нормальной форме, если А* - определена (то есть в А

(X1 X2 (X2 X1 )) .

Решение. Используя законы де Моргана, получаем:

(СДНФ) данной ПФ относительно переменных X1, X2, ... Xk называют такую ее ДНФ, в которой в каждой элементарной конъюнкции на r-м месте (1 r k) обязательно находится или переменная Xr или ее отрицание.

Совершенной конъюнктивной нормальной формой

12

(СКНФ) данной ПФ относительно переменных X1, X2, ... Xk называют такую ее КНФ, в которой в каждой элементарной дизъюнкции на r-м месте (1 r k) обязательно находится или переменная Xr или ее отрицание.

Рассмотрим два способа перехода к совершенным формам – аналитический и табличный. При аналитическом приведении ДНФ к СДНФ следует элементарные конъюнкции, в которые входят не все переменные, умножить на дизъюнкцию недостающей переменной с ее отрицанием, затем в соответствии с дистрибутивным законом раскрыть скобки и исключить повторения.

Приведение КНФ к СКНФ осуществляется аналогично, но только к элементарным дизъюнкциям, содержащим не все переменные, прибавляют нули, представленные в виде конъюнкций каждой недостающей переменной с ее отрицанием.

При табличном способе приведения к СДНФ составляется таблица истинности данной ПФ. Затем рассматриваются те строки, в которых формула принимает истинностное значение 1. Каждой такой строке ставится в соответствие элементарная конъюнкция, в которую переменная, принимающая истинностное значение 1, входит без отрицания, а 0 – с отрицанием. После этого образуется дизъюнкция всех элементарных конъюнкций, которая и составляет СДНФ.

При приведении к СКНФ рассматриваются те строки таблицы истинности, в которых формула принимает значение 0. Каждой такой строке ставится в соответствие элементарная дизъюнкция, причем переменная, принимающая значение 1, входит в нее с отрицанием, а 0 – без отрицания. Затем образуется конъюнкция всех полученных элементарных дизъюнкций, которая и составляет СКНФ.

Заметим, что из табличного способа построения совершенных нормальных форм следует, что тождественно-лож- ные формулы не имеют СДНФ, а тождественно-истинные не имеют СКНФ. Если же для ПФ существуют СДНФ и СКНФ, то они единственны. Поэтому две ПФ, имеющие совпадающие СДНФ (СКНФ) обязательно равносильны.

13

Пример 7. Составим СДНФ и СКНФ для формулы

= 1, а Y = 0, поэтому элементарная конъюнкция имеет вид Х

Y . В третьей строке Х = 0, а Y = 1, следовательно, ей соот-

ветствует конъюнкция X Y. Объединяя полученные конъюнкции связкой дизъюнкции получим СДНФ для : = (Х

Y ) ( X Y).

Для построения СКНФ отметим строки, в которых = 0. (первую и четвертую). Составим элементарные дизъ-

юнкции X Y (для первой строки) и X Y (для четвертой строки). Соединяя их в конъюнкцию, получаем СКНФ для :

Табличный способ построения СДНФ и СКНФ может быть использован и для построения ПФ по заданной булевой функции.

Пример 8. Для булевой функции, заданной табл. 9 составить ПФ.

Решение. Для тех строк, в которых f = 1, составляем эле-

ментарные конъюнкции: (Х1 Х2 Х3), (Х1 X 2 X3 ),

14

7. МНОГОЧЛЕНЫ ЖЕГАЛКИНА

Рассмотрим булеву функцию f (X, Y) = X + Y, где под сложением подразумевается сложение по модулю 2.

Вместо символа конъюнкции ( ) в данном случае удобно писать символ · или вообще его опускать, как это делается в арифметике. Тогда функцию X Y можно записать как X·Y или просто XY. Составим таблицу истинности для

функции X + Y и XY. (табл. 10). Условимся, что X = X + 1. По таблице истинности нетрудно проверить, что выпол-

няются тождества:

15

X + Y = Y + X; XY = YX; X·(Y + Z) = XY + XZ; 0 + X = 0;

0 ·X = 0; 1·X = X; X + X = 0; X·X = X.

Все соотношения, кроме двух последних, аналогичны обычным правилам алгебры многочленов. Поэтому булеву функцию можно представить в виде многочлена от своих переменных.

Многочленом Жегалкина называется многочлен, являющийся суммой константы 0 и 1 и различных одночленов, в которые все переменные входят не выше, чем в первой степени.

Для представления формулы многочленом Жегалкина необходимо, используя равносильности, перейти в формуле только к конъюнкциям и отрицаниям (причем отрицаниям не всегда тесным), конъюнкции заменить умножением, а отри-

цания преобразовать по равенству X = X + 1. В информатике операция отрицания, которая меняет значение 0 на 1 и 1 на 0 называется инверсией.

Пример 9. Представить многочленом Жегалкина функ-

ции X Y Z, X Y Z .

Решение.1) Используя равносильность 18), получаем:

X Y Z = X Y Z = X Y Z = X Y Z =

=(X + 1)(Y + 1)(Z + 1) + 1 = XYZ + XY + XZ + Z + YZ +

+Y +1 + 1 + Z = XYZ + XZ + YZ + X + Y + Z.

2)Переходя к конъюнкциям и отрицаниям, получаем:

X Y Z = (X Y Z) = (XY + 1)(Z + 1) + 1 =

= XYZ + XY + Z + 1 + 1 = XYZ + XY + Z.

Можно показать [3], что каждая булева функция может быть представлена многочленом Жегалкина и притом единственным образом.

16

8. АЛГОРИТМЫ ПОСТРОЕНИЯ МНОГОЧЛЕНА ЖЕГАЛКИНА

Рассмотрим алгоритмы построения многочлена Жегалкина булевой функции, заданной различными способами: совершенной ДНФ, произвольной ДНФ и таблицей истинности.

Алгоритм построения многочлена Жегалкина по СДНФ.

Пусть задана совершенная ДНФ функции f x1,..., xn .

Шаг 1. Заменяем каждый символ дизъюнкции на символ дизъюнкции с исключением.

Шаг 2. Заменяем каждую переменную с инверсией X равносильной формулой X 1.

Шаг 3. Раскрываем скобки.

Шаг 4. Вычеркиваем из формулы пары одинаковых слагаемых.

Таким образом, получаем многочлен Жегалкина функ-

Пусть задана произвольная ДНФ функции f x1,..., xn .

Шаг 1. Разбиваем ДНФ на пары конъюнкций. Если число конъюнкций нечетно, одна из них остается без пары.

Шаг 2. Заменяем дизъюнкцию каждой пары конъюнкций K1 K2 формулой K1 K2 K1K2 .

Шаг 3. В полученной формуле находим очередную дизъюнкцию A1 A2 и заменяем ее формулой A1 A2 A1 A2 . Повторяем шаг 3 до тех пор, пока это возможно.

17

Шаг 4. Заменяем каждую переменную с инверсией X равносильной формулой X 1.

Шаг 5. Раскрываем скобки.

Шаг 6. Вычеркиваем из формулы пары одинаковых слагаемых.

Таким образом, получаем многочлен Жегалкина функ-

ции f x1,..., xn .

Пример 11. Найдем многочлен Жегалкина булевой

Алгоритм построения многочлена Жегалкина по табли-

це истинности основан на методе неопределенных коэффициентов.

Продемонстрируем идею метода на примере произвольной булевой функции двух аргументов f X ,Y . Представим

ее многочленом Жегалкина с неизвестными коэффициентами:

Pf c0 c1Y c2 X c3 XY .

Подставив в данное равенство наборы значений аргументов, получим систему из четырех линейных уравнений с четырьмя неизвестными c0 , c1, c2 , c3 :

Заметим, что наборы подставлены в равенство в естественном порядке, и система имеет треугольный вид: в первом уравнении обратились в ноль все слагаемые, следующие за

18