
Учебное пособие 800318
.pdf
x905:5 181B.
Вслучае статистического ряда (когда значению параметра соответствует какая-либо частота) средняя арифметическая величина вычисляется по формуле:
|
|
1 |
|
k |
|
|
|
|
|
|
|||
x |
|
|
i 1 |
xm , |
(7.2) |
|
|
||||||
|
|
n |
i i |
|
||
k
где n mi.
i1
Вэтом случае среднюю называют средней взвешенной.
Пример 2. Для упорядоченного ряда, число интервалов k=32:
|
|
1 |
179 1 180 1 ... 209 2 210 1 |
31196 |
194.975 B. |
|
x |
||||||
|
|
|||||
160 |
160 |
|
||||
Аналогично вычисляется средняя арифметическая интервального ряда с той только разницей, что в качестве значения параметра следует принимать середины интервалов:
|
|
1 |
178 1 181 3 ... 208 5 211 1 |
31192 |
194.95B. |
|
x |
||||||
|
|
|||||
160 |
160 |
|
||||
Вследствие различной ширины интервалов рассматриваемых рядов обе средние частично не совпадают.
Следует подчеркнуть, что средняя только в том случае является обобщающей характеристикой, когда она применяется к однородной совокупности статистического материала,
Кроме важнейшей характеристики положения — средней — при анализе и контроле качества приходится встречаться и с другими характеристиками положения, в частности медианой и модой случайной величины.
Если полученные при измерениях значения расположить в возрастающем или убывающем порядке, то медианой будет значение Me, занимающее серединное значение в ряду. Таким образом, медиана — это значение
21

параметра, которое делит упорядоченный ряд на две равные по объему группы. При нечетном числе измерений, т. е. при n =2i+1, значение параметра для случая i+1 будет медианным. При четном числе измерений (2i) медианой является средняя арифметическая двух значений, расположенных в середине ряда.
Таким образом, формулы для вычисления медианы имеют следующий вид:
Me xi 1 |
(7.3) |
для случая нечетного числа измерений; |
|
Me xi xi 1 /2 |
(7.4) |
для случая четного числа измерений. |
|
Пример 3. Возьмём пять первых значений пробивного напряжения (х1=179, х2=180, х3=181, х4=182, х5=183),т.е.
нечётное число измерений, расположенных в возрастающем порядке. Находим для зтих пяти значений медиану: (2i+1)=5, откуда 2i=4, i=2. По формуле (2.5) получим
Me xi 1 x2 1 x3 181B.
Если взять только четыре первых значения пробивного напряжения (х1=179,х2=180,х3=181,х4=182), т. e. четное число измерений, то 2i=4, i=2. По формуле (7.4),
Me xi xi 1 x2 x3 180 181 180.5B. 2 2 2
Значение медианы легко определяется графически с помощью кумулятивной кривой (см. рис. 6.3). Так как по оси ординат отложены накопленные частоты, то, разделив отрезок ординаты, соответствующий 100% наблюдений, пополам и восстановив из его середины перпендикуляр, мы получим медиану геометрически как абсциссу точки пересечения перпендикуляра с кумулятивной кривой.
Модой случайной величины называется значение параметра, которое наиболее часто встречается в данном ряду. Условимся обозначать моду через Мо. Для дискретного ряда
22
мода определяется по частотам наблюдаемых значений параметра качества и соответствуют значению параметра с наибольшей частотой.
В случае непрерывного распределения с равными интервалами модальный (т.е. содержащий моду) интервал определяется по наибольшей частоте; в случае неравных интервалов - по наибольшей плотности. Плотность вычисляется как отношение частоты к продолжительности интервала.
Средние величины, характеризуя однородную совокупность одним числом, не учитывают рассеивание наблюдаемых значений параметра качества. Для отображения рассеивания в математической статистике применяют ряд характеристик. Самый простой из них является размах R. Размах представляет собой величину неустойчивую, зависящую от случайных обстоятельств и поэтому применяемую, как правило, в качестве приблизительной оценке рассеивания. Однако, как будет показано ниже, размах бывает очень удобно применять в контрольных картах. Размах R сравнительно легко вычисляется как разность между наибольшим и наименьшем значениями ряда наблюдений:
R = xmax - xmin |
(7.5) |
Другая статистическая характеристика рассеивания наблюдаемых значений показывает, как тесно группируются отдельные значения вокруг средней арифметической или как они рассеиваются вокруг этой средней. Так как алгебраическая сумма отклонения отдельных значений xi от средней арифметической x равна нулю и непригодна в качестве меры рассеивания, за меру рассеивания принимают сумму квадратов отклонений отдельных значений от средней арифметической, делённую на число наблюдений, уменьшенное на единицу. Эту меру называют выборочной дисперсией и обозначают через s2. Для простой статистической совокупности[1-4],
23
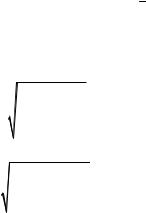
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
2 |
|||
|
|
x |
||||||||
|
s2 |
i 1 |
|
|
|
(7.6) |
||||
|
|
|
|
|
||||||
|
|
|
n 1 |
|||||||
|
При наличии частот mi |
|
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
|
|
|
|
|
xi |
|
2 mi |
||||||
|
x |
|||||||||
|
s2 |
i 1 |
|
(7.7) |
||||||
|
|
|
||||||||
где |
|
|
n 1 |
|||||||
k |
|
|
|
|
|
|
|
|||
n mi . |
|
|
|
|
|
|
|
|||
i 1
Вместо выборочной дисперсии s2 часто применяют выборочное стандартное отклонение s. Оно имеет ту же
размерность, что и средняя арифметическая x. Выборочное стандартное отклонение для простой статистической совокупности и при наличии частот определяется соответственно по следующим формулам:
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
2 |
|
||||
|
|
x |
(7.8) |
||||||||
s |
|
i 1 |
|
|
; |
||||||
|
|
|
|
||||||||
|
|
|
n 1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
xi |
|
2 mi |
|
||||||
|
|
x |
(7.9) |
||||||||
s |
i 11 |
|
; |
||||||||
|
|
||||||||||
|
|
|
n 1 |
|
|||||||
Отношение стандартного отклонения к средней арифметической, выраженное в процентах, называют
коэффициентом вариации V: |
|
||
V |
s |
100 |
(7.10) |
|
|||
|
x |
|
|
Коэффициент вариации, который также используется как статистическая характеристика рассеивания, показывает относительное колебание отдельных значений около средней арифметической. Коэффициент вариации, являясь безразмерным, удобен для сравнения рассеивания случайной величины с её средним значением.
ЛЕКЦИЯ 3
24

8. Математическое ожидание и дисперсия
Рассмотрим такое понятие в теории вероятностей как математическое ожидание. Математическое ожидание играет роль характеристики положения случайной величины в генеральной совокупности, и поэтому его иногда называют генеральным средним арифметическим значением случайной величины или центром группирования значений случайной величины в генеральной совокупности.
Рассмотрим случайную величину X, которая может принимать дискретные положения x1 ,х2 ,х3 ,.., хi ,.... хn с соответствующими вероятностями p1 ,р2 ,р3 ,…pi ,…,pn . Нам требуется охарактеризовать каким-то числом положение значения случайной величины на оси абсцисс с учетом того, что эти значения имеют различные вероятности. Для этой цели воспользуемся формулой для средней взвешенной, где каждое значение хi при усреднении должно учитываться с «весом», пропорциональным вероятности этого значения. Тогда
генеральное среднее арифметическое значение случайной вели-
чины X, которое обозначим М(х), может быть подсчитано по формуле
M (x) x1 p1 x2 p2 ... xn pn p1 p2 ... pn
n
или, учитывая, что pi 1,
i 1
n
M(x) xi pi
i 1
n
xi pi
i 1 |
, |
(8.1) |
n |
pi
i 1
(8.2)
25
Вычисленная выборочная средняя всегда будет содержать элемент случайности, в то время как математическое ожидание, представляющее среднее значение случайной величины в генеральной совокупности, является величиной постоянной для данной генеральной совокупности. При большом количестве наблюдаемых значений выборочная средняя приближается к математическому ожиданию.
Дисперсию случайной величины X в генеральной совокупности, которую будем обозначать через σ2,
подсчитывают по следующим формулам: |
|
|
|
|||
для случая, когда значения хi |
в генеральной |
|||||
совокупности не повторяются, |
|
2 |
|
|
||
|
|
n |
|
|
|
|
2(x) |
[M(x) xi ] |
(8.3) |
||||
i 1 |
|
|
|
|||
n |
|
|
|
|||
|
|
|
|
|
|
|
для случая, когда значения хi повторяются, |
||||||
|
n |
2 |
|
|
|
|
2 (x) |
[M(x) xi ] |
|
mi |
|
||
i 1 |
|
|
|
|
||
|
|
|
|
(8.4) |
||
|
|
n |
|
|
|
|
n |
|
|
|
|
||
где n mi
i 1
Кроме характеристик положения и рассеивания нам в дальнейшем придется столкнуться с рядом характеристик, каждая из которых описывает то или иное свойство распределения. В качестве этих характеристик чаще всего применяются так называемые центральные моменты.
Практический интерес представляют второй, третий и четвертый центральные моменты. Второй центральный момент представляет собой не что иное, как дисперсию.
Третий центральный момент служит для характеристики асимметрии распределения:
26

n
mi (x xi )3
MЗ i 1 (8.5)
n
mi
i 1
Если распределение симметрично относительно его среднего значения, то взвешенные по соответствующим частотам кубические отклонения значений случайной величины, равноотстоящие от средней арифметической, отличаются только знаками и их сумма равна нулю. Если же распределение асимметрично, то значения параметра, лежащие по одну сторону от средней арифметической, дадут большие кубические отклонения, чем значения, лежащие по другую сторону. Знаки этих отклонений различны. Разность между суммами положительных и отрицательных слагаемых будет отличаться от нуля, являясь положительной или отрицательной. Соответственно этому знак М3 указывает на отрицательную или положительную асимметрию.
Чтобы получить меру асимметрии в виде отвлеченного числа, позволяющего сравнивать разнородные распределения, третий момент М3 делят на куб стандартного отклонения σ3. Полученная величина, обозначаемая А, носит название асим-
метрии или косости распределения:
А = М3 / σ3 (8.6)
Величина асимметрии дает нам представление о большей или меньшей асимметрии, а знак указывает на ее направление: если А>0, то средняя лежит справа от моды (правосторонняя асимметрия); если А<0, то средняя лежит слева от моды (левосторонняя асимметрия).
Кроме значения А за меру асимметрии иногда принимают число
а=(x-Мо)/ σ, |
(8.7) |
которое часто называют коэффициентом асимметрии Особенностью симметричных рядов является равенство
трех характеристик — средней арифметической, моды и
27

медианы: x = Мо = Ме. Поэтому а для симметричных распределений равно нулю.
Четвертый центральный момент М4 служит для характеристики так называемой крутости, т. е. островершинности или плосковершинности распределения. Это свойство распределения описывается с помощью так называемого эксцесса.
Эксцесс случайной величины X вычисляется по формуле
Эк=М4 / σ4 -3. |
(8.8) |
Число 3 вычитается из отношения М4 / σ4 потому, что для весьма важного и широко распространенного в природе гауссовского закона распределения, с которым мы подробно познакомимся в дальнейшем, М4 / σ4 = 3. Поэтому для гауссовского распределения эксцесс равен нулю. Кривые, более островершинные по сравнению с ним, обладают положительным эксцессом; кривые более плосковершинные — отрицательным эксцессом.
9.Основные законы распределения случайной величины
Вобщем случае для определения вероятности того, что случайная величина X примет некоторое заранее заданное значение (или окажется меньше его), необходимо знать закон распределения случайной величины. Ввиду того что случайные величины могут быть как дискретными, так и непрерывными, распределения их вероятностей будут описываться соответственно законами распределения дискретных и непрерывных случайных величин [1].
28
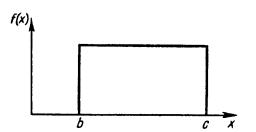
Рис. 9.1. Равновероятное (прямоугольное) распределение
Законы распределения для дискретных случайных величин, применяемые при контроле выпускаемой продукции, подробно рассмотрены в [2], поэтому в данном разделе рассмотрим законы распределения для непрерывных случайных величин, причем только те, которые необходимы для понимания последующего материала.
Равновероятный закон. Простейшим распределением для непрерывной случайной величины Х является равновероятный (равномерный, прямоугольный) закон распределения (рис. 9.1).
Случайная величина X распределена по равновероятному закону, если плотность вероятности
|
0 |
при |
x b |
|
|
|
|
|
(9.1) |
f (x) 1/(с b)приb x c |
||||
|
0 |
при |
x c |
|
|
|
|||
Плотность вероятности f(x) иногда называют дифференциальной функцией распределения. Ее физический смысл рассмотрим несколько позже. Нетрудно убедиться в том, что площадь под кривой распределения равна единице. Действительно,
|
c |
1 |
|
|
|
|
f (x)dx |
dx 1 |
(9.2) |
||
|
|||||
|
b |
c b |
|
||
|
29 |
|
|
|
|

Кроме плотности вероятности для непрерывных распределений используется также интегральная функция распределения F(x), которая в общем виде выглядит следующим образом:
X
|
F(x) f (x)dx |
(9.3) |
|
|
|
|
|
Для |
равновероятного |
закона |
распределения |
интегральная функция
(9.4)
Физический смысл интегральной функции распределения состоит в том, что она представляет собой вероятность попадания случайной величины х в интервал от -∞ до X, где X — определенное, наперед заданное число.
Гауссовский закон распределения. На практике часто приходится иметь дело с распределениями, которые незначительно отличаются от гауссовского. Широкое распространение гауссовского закона распределения находит теоретическое объяснение в центральной предельной теореме, смысл которой заключается в следующем. Предположим, что параметр качества Y исследуемого объекта зависит от к действующих на него независимых между собой (или слабо зависимых) факторов Х1, Х2, Х3, ..., Хк, образующих в каждый момент времени совокупность случайных независимых (или слабо зависимых) случайных величин х1, х2, х3, ..., хк, одновременно воздействующих на качество изделия. Если число этих независимых случайных величин велико (приближаясь в пределе к бесконечности) и среди них отсутствуют случайные величины с резко отличающимися от других случайных величин средними
30
