Учебное пособие 800316

направления этой силы деформирование на этом участке называют растяжением или сжатием.

Если в поперечных сечениях стержня возникают только крутящие моменты МК, то деформирование называют чистым кручением или просто кручением.

Если в поперечных сечениях возникают только изгибающие моменты Мy (Мx), то деформирование называют чистым изгибом.

Если же наряду с изгибающими моментами возникают поперечные силы Qx (Qy) то изгиб называют поперечным .

Прочие случаи относят к сложному сопротивлению. Внутренние силы распределены каким-то образом по се-

чению тела. Выделим в этом сечении некоторую достаточно малую область площадью ∆F и обозначим равнодействующую

внутренних сил, действующих на этой площадке, через Р (рис. 1.3) . Тогда величину

р lim ( р / F )

F 0

называют вектором полного напряжения в точке. В общем случае получаем вектор, произвольно ориентированный в пространстве. Проекцию этого вектора на нормаль к площадке обычно обозначают 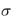и называют нормальным напряжением. Проекцию на плоскость сечения обычно обозначают η и называют касательным напряжением.

Таким отраазом, напряжение - это интенсивность внутренних сил. Размерность напряжения - Н/м2.

1.4. Перемещения и деформации Как уже указывалось, в сопротивлении материалов тела

рассматриваются как деформируемые. При этом, как правило, рассматриваются лишь кинематически неизменяемые системы, т.е. системы, на которые наложены связи, исключающие их движение в пространстве как жесткого целого. Поэтому будем считать, что тело зафиксировано в пространстве некоторой системой опор (рис. 1.4). Приложение нагрузок к этому телу

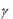
называют угловой деформацией или сдвигом. Величины 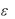и служат количественной мерой деформации.

1.5. Основные принципы сопротивления материалов I.5.I. Закон Гука

Основные свойства или, как говорят, модель материала в сопротивлении материалов определены законом Гука. Согласно этому закону перемещения в определенных пределах пропорциональны вызвавшим их нагрузкам. Так, перемещение uХ некоторой точки тела А под действием нагрузки (силы, момента и т.д.) Р, приложенной в точке В, будет равно

uX=kP,

где коэффициент пропорциональности k зависит от свойств материала, положений точек А и В, направлений оси X и нагрузки Р, размеров и формы тела, условий его закрепления.

В современной трактовке по закону Гука деформации пропорциональны соответствующим напряжениям. Причем в случае изотропного материала коэффициенты пропорциональности уже зависят только от свойств материала и поэтому могут рассматриваться как его механические характеристики. В этой форме pакон Гука и будет использован нами в дальнейшем.

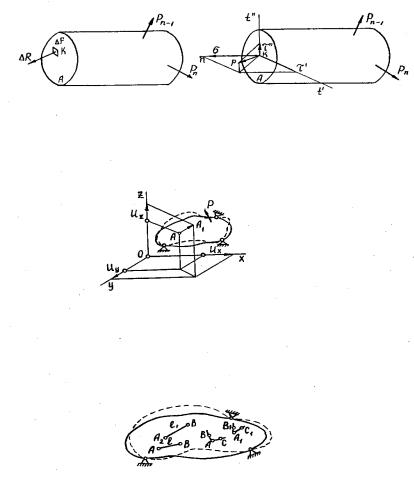
Рис. 1.3

Рис. 1.4

Рис. 1.5

1.5.2. Принцип независимости действия сил (принцип суперпозиции)

Согласно этому принципу перемещения и внутренние силы в упругом теле не зависят от порядка приложения нагрузок. Это позволяет определять перемещения, внутренние силы, деформации и напряжения в случае, когда тело находится под действием некоторой системы нагрузок, как суммы пере-

мещений, внутренних сил, деформаций и напряжений, возникающих при действии каждой из нагрузок в отдельности .

Убедимся в справедливости этого принципа на примере определения перемещения. Пусть к телу приложена сила Р1 . Точка А переместится в направлении оси x под действием си-

ся. Различие в ситуациях, которым соответствуют равенства (1.2) и (1.3), заключается в том, что в последнем случае, наряду с силой Р2, действует сила Р1. Следовательно, различие к2 и к21 означало бы зависимость этого коэффициента от силы P1 , что противоречит закону Гука (второе слагаемое равенства (1.3) оказывается нелинейной функцией нагрузок). Следовательно, к1=к21, что и доказывает справедливость равенства

uX=uX(1)+uX(2) .

Заметим, что поскольку, как уже указывалось, коэффициенты пропорциональности перемещений нагрузке зависят от геометрии и размеров тела, равенство К1=К21 справедливо лишь в случае, если при нагружении тела силой Р1 произошли пренебрежимо малые изменения размеров .

Из справедливости принципа суперпозиции по отношению к перемещениям следует его справедливость по отношению к деформациям, а в силу пропорциональности деформаций напряжениям - относительно напряжений.

1.5.3. Принцип начальных размеров В сопротивлении материалов рассматриваются деформа-

ции, при которых перемещения любой точки малы по сравнению с размерами тела. Это позволяет при записи уравнений равновесия и некоторых других уравнений рассматривать тело как недеформированное, т.е. считать, что при нагружении тела его размеры не изменяются .

1.5.4. Принцип Сен-Венана Согласно этому принципу характер приложения нагрузки

влияет на напряженное состояние лишь в области, распространяющейся на величину характерного размера поперечного сечения от места приложения нагрузки (например, если поперечное сечение стержня круглое, то на величину диаметра этого сечения). В дальнейшем будем считать, что эта область исключена из рассмотрения.

На рис.I.6. показаны стержни, растягиваемые различным образом приложенными к их концам силами Р. В соответствии с принципом Сен-Венана будем считать их напряженное состояние одинаковым.

2.РАСТЯЖЕНИЕ И СЖАТИЕ

2.1.Условия прочности при растяжении и сжатии [1] 2.1.1 Внутренние силы при растяжении и сжатии Как уже указывалось, растяжением или сжатием называ-

ется деформирование, при котором в поперечных сечениях стержня возникают только нормальные силы. Нормальная сила, направленная от сечения, считается положительной; если же она направлена к сечению, то - отрицательной. Если в поперечных сечениях возникает положительная нормальная сила деформирование называется растяжением, если отрицательная, то - сжатием.

На рис.2.1 приведен пример стержня. Для определения нормальной силы в сечении I-I воспользуемся методом сечений. Будем рассматривать равновесие части стержня, расположенной под указанным сечением. Для того, чтобы обеспечить автоматический учет знаков, направим определяемую нормальную силу N от сечения.

Запишем далее уравнение равновесия, проецируя все силы на ось z, совпадающую с внешней нормалью к сечению:

k

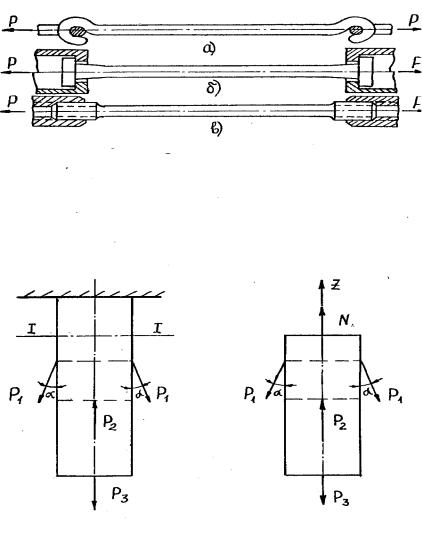
N 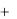Pnz 0 ,

n 1

–проекции внешних сил, приложенных к рассматриваемой части стержня, на ось z; k – число приложенных внешних сил. Из этого уравнения получим

k

N 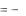Pnz . n 1

Таким образом, нормальная сила в любом сечении равна сумме проекций всех внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, на ось, параллельную внешней нормали к сечению, но имеющую противоположное ей направление. Направление внешней нормали опре-

деляется тем, равновесие какой части стержня рассматривается.

Рис. 1.6

Рис. 2.1

2.1.2. Напряжения при растяжении и сжатии В поперечных сечениях стержня возникает нормальная

сила, следовательно, в них возникают нормальные напряжения. Предположим, что в указанных сечениях возникают только равномерно распределенные нормальные напряжения. Это позволяет определить напряжения по простой формуле

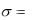NF ,

где F площадь поперечного сечения стержня до нагружения. 2.1.3. Условия прочности Наблюдения показывают, что разрыв стержней из одного

материала происходит практически при одном и той же напряжении. Это позволяет писать условие прочности растягиваемого стержня в виде

где [ζ]p - допускаемое напряжение при растяжении. Как назначается это напряжение, будет выяснено ниже.

Условие прочности при сжатии записывается аналогично

N

F с ,

где [ζ]с - допускаемое напряжение при сжатии.

При равенстве допускаемых напряжений [ζ]р = [ζ]с = [ζ] можно условия прочности объединить

N

F

.

Если требуется подобрать поперечное сечение стержня, то

исходят из неравенства