Учебное пособие 2015

Переходные и установившиеся процессы в РИЭС удобно исследовать на разностной фазовой плоскости, если объект аппроксимируется последовательным соединением линейного инерционного звена первого порядка и безынерционного квадратичного нелинейного звена с характеристикой

z k H x 2 (см. рис. 2.9, W2 ( p) = 1, у = z). Разностная фазовая

плоскость, предложенная Дж. Эслтайном и В. М. Кунцевичем [26], является дискретным аналогом обычной фазовой плоскости. По оси абсцисс на фазовой плоскости

Разностное уравнение, описывающее динамику такой системы, имеет вид [26]

постоянная времени исполнительного сервомотора. Обозначив x xS xS 1 и решая (2.64), получим

уравнение фазовых траекторий [26]

Уравнение (2.75) определяет кривые 1 и 2, являющиеся границами переключения на разностной фазовой плоскости

(рис. 2.16).

С учетом границ переключения легко построить фазовый портрет системы разностной фазовой плоскости по уравнению (2.15), (рис. 2.16). Построение фазового портрета значительно облегчается, если учесть, что ордината данной точки является приращением абсциссы для последующей точки по определению разностной фазовой плоскости

( S xS xS 1 ). Из рис. 2.16 видно, что в системе устанавливается предельный цикл с полупериодом N=4.

2.3. Помехоустойчивость импульсных экстремальных систем.

В этом параграфе рассматриваются вопросы, связанные с изучением поведения импульсных экстремальных систем, находящихся под воздействием статистически заданных внешних возмущений и помех. Выше были описаны разные по принципу действия импульсные экстремальные системы: шаговые автоколебательные, импульсные с двумя пробными шагами, импульсные с разностным синхронным детектором. Единого метода исследования всех этих систем нет, но в ряде случаев при наложении дополнительных ограничений многие из них могут быть исследованы одними и теми же методами. Ограничения и упрощающие допущения играют решающую роль при выборе того или иного метода исследования.

Общими допущениями являются следующие:

δ — помеха, искажающая истинное значение показателя качества, приведена всегда к выходу объекта и суммируется с показателем качества;

153

λ — внешнее возмущение, перемещающее положение экстремума параллельно оси регулирующих воздействий, приведено всегда ко входу безынерционного нелинейного элемента и не коррелировано со значением помехи

(рис. 2.17,а).

Внастоящее время можно выделить по крайней

мере три основных направления в исследовании импульсных экстремальных систем. Остановимся на каждом из них.

Вряде случаев можно пренебречь влиянием инерционной части объекта управления и исполнительного устройства. При этом для исследования влияния помех на установившиеся режимы работы экстремальных систем с двумя пробными шагами и шаговых автоколебательных систем может быть применен аппарат исследования цепей Маркова [34, 35, 45, 66].

Рассмотрим экстремальную систему с двумя пробными шагами. Положим, что величина рабочего изменения регулирующих воздействий постоянна и равна (или в целое число раз больше) пробному шагу

где k может быть 1, 2, 3, …

Тогда изменение регулирующего воздействия будет про-

154

исходить согласно следующему соотношению:

исполнительного устройства. Полагаем, что помеха S

принимает независимые случайные значения, закон распределения которых известен.

Будем считать, что одно из возможных значений регулирующего воздействия совпадает с положением экстремума. Тогда остальные возможные положения рабочей точки будут удалены от экстремума на вполне определенные расстояния (рис. 2.42,6). Пронумеруем эти возможные состояния, обозначив точку положения экстремума через 0.

155

Рис. 2.42. К помехоустойчивости безынерционных ИЭС. а—схема объекта управления;

б — экстремальная характеристика объекта.

Если система находится в каком-то состоянии, то после выполнения пробных движений возможны три варианта дальнейшего поведения системы:

1)система совершает рабочий шаг по направлению к экстремуму (помеха не искажает работу системы);

2)система совершает рабочий шаг от экстремума

(помеха вызывает ложные срабатывания экстремального регулятора);

3) система не изменит положения рабочей точки. Обозначим вероятности движений для всех трех случаев соответственно через pi , qi и mi .

Индекс i определяет здесь положение рабочей точки на экстремальной характеристике. Очевидно, что

156

т. е. перечисленные выше три случая движения системы составляют полную систему событий.

Для случая, когда диапазон изменения регулирующего воздействия ограничен, в состояниях N1 и N1 (где N1 иN1 соответствуют граничным значениям регулирующего

воздействия справа и слева от экстремума) выражение (2.78) в этих точках будет принимать значения

p N1 m N1 pN 2 mN 2 1 . (2.78а)

Вероятности перехода системы из одного состояния в другое ( pi , qi и mi ) зависят только от положения рабочей

точки и не зависят от предыстории движения. Таким образом, при указанных допущениях процессы в системе могут быть описаны простой дискретной цепью Маркова с конечным или бесконечным числом состояний (первое означает, что диапазон изменения регулирующего воздействия ограничен и заданы так называемые условия отражения [43—45, 66], второе означает, что на диапазон изменения регулирующего воздействия практически никаких ограничений не налагается

[66, 56—59]).

где Р — закон распределения амплитуды помехи. Оценить точность работы системы можно, по крайней

мере, по двум критериям:

1)среднего отклонения системы от положения экстремума;

2)среднего времени поиска экстремума θ. Первая оценка может быть вычислена так:

157

где θ[i] — состояние рабочей точки системы;

Р[i] — вероятность того, что система находится в

состоянии

i(i 0, 1, 2,...., N,...., ) .

Вторая оценка может быть определена как среднее время перехода из состояния i в состояние i + j:

S 1

где t(i,i j) время перехода из состояния i в состояние j за время s;

P[i,i j, s] вероятность того, что система перейдет из

состояния i в состояние j за время s.

Чтобы посчитать оценку качества работы системы, необходимо знать все значения вероятностей PS (i) и

P[i,i j, s] .

В первом случае неизвестные значения Р [i] могут быть определены как решение системы уравнений

………………………………………………………………………

…………………………………………………………………........

………………………………………………………………………

………………………………………………………………………

Полагая, что экстремальная характеристика симметрична относительно точки экстремума, и учитывая, что

P[0] 2 P[i] 1.

i 1

Для случая, когда экстремальная характеристика объекта аппроксимируется двумя отрезками симметричных прямых

Для случая, когда диапазон изменения регулирующего воздействия фиксирован, выражение (2.85) может быть записано так:

В выражениях (2.85), (2.85а) и (2.85б) величины p и q определяются так:

Для случая, когда характеристика объекта аппроксимируется параболой, выражения (2.85), (2.85а) могут быть переписаны в виде

Среднее время перехода из одного состояния в другое может быть определено после решения системы уравнений

(для j > 0 и для j < 0) [6, 35]:

Ti ( j) piTi 1 ( j 1) miTi ( j) qiTi 1 ( j 1) 1

для всех i = 1, 2 ... N-j при положительных j и для всех i = j+1, j+2, ... N при отрицательных j. Здесь N — число возможных состояний системы.

160

Решение этого уравнения [6, 35] может быть представлено в виде

Для случая, когда характеристика объекта аппроксимируется двумя отрезками прямых и m = 0:

Используя соотношения (2.85)—( 2.85в), можно проанализировать поведение экстремальной системы с двумя пробными движениями при воздействии на нее случайной помехи. В случаях, когда необходимо уменьшить вредное влияние случайной помехи, можно увеличить число пар пробных шагов на объекте, прежде чем совершается рабочий шаг, В ряде случаев, особенно если система работает почти все время в установившемся режиме (возмущение λ не меняется), такой способ дает заметный выигрыш по сравнению с ранее описанным.

Рассмотрим шаговую автоколебательную систему. Согласно закону изменения регулирующего воздействия система при срабатывании импульсного элемента обязательно переходит в новое положение, а направление движения

и предыдущим, поэтому mi 0, pi qi 1. Процесс в системе

будет отличаться от описанного и может быть представлен в виде сложной цепи Маркова [34].

Под pi будем понимать теперь уже условную вероят-

161

ность того, что система из i-го состояния сделает шаг по направлению к экстремуму при условии, что предыдущий шаг из состояния (i+1) тоже был сделан в сторону экстремума.

а под величиной qi будем понимать условную вероятность

того, что система из состояния i сделает шаг от экстремума при условии, что предыдущий шаг из состояния (i -1) был также сделан от экстремума

Используя методику, аналогичную приведенной в [34], для случаев аппроксимации экстремальной характеристики параболой и двумя отрезками прямых получаем следующие соотношения для вычисления M[θ]:

В [34] приведено соотношение для выбора оптимальной величины шага регулирования в случае, когда помеха имеет гауссовский закон распределения с математическим ожиданием, равным нулю. Это соотношение имеет вид

где ζ — величина среднеквадратического отклонения помехи;

k 2 1. 2

2.3.1. Шаговая «экстремальная система с двумя пробными шагами.

Несколько другой подход к исследованию помехоустойчивости импульсных экстремальных систем позволяет определить оптимальные параметры экстремального регулятора при учете случайного дрейфа экстремальной характеристики объекта и случайной помехи, искажающей значение показателя качества.

Критерием оценки точности экстремальной системы может служить величина среднего отклонения показателя качества от экстремума.

Синтез экстремальной системы заключается в таком выборе закона изменения регулирующего воздействия и параметров регулятора, чтобы величина D была минимальной

Закон изменения регулирующего воздействия ищем в

виде

j 1

где W j — коэффициент веса, с которым учитывается величина j ;

j — сигнал, пропорциональный отклонению рабочей

точки от экстремума.

Предполагается, что экстремальная характеристика объекта с достаточной степенью точности аппроксимируется параболой вида (2.54).

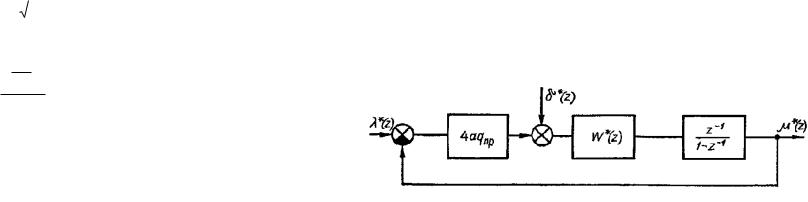
Рис. 2.18. Эквивалентная блок-схема ИЭС.

Помеха суммируется со значением показателя качества и является случайной независимой функцией времени типа «белого шума». Разработанная в [75] методика пригодна для исследования двух типов экстремальных систем: шаговой экстремальной системы с двумя пробными шагами и шаговой экстремальной системы с модулирующим воздействием. Остановимся более подробно на применении методики [75] к исследованию этих систем.

164

Значения измеряемого показателя качества с учетом влияния помех, исходя из (2.10), будут

Выражение (2.98) действительно при предположении, что 0 0 . Эквивалентная уравнениям (2.97) и (2.98) блоксхема системы показана на рис. 2.18. Из уравнений (2.41) и (2.42), исключив промежуточную переменную (z) , можно получить

назовем импульсной передаточной функцией замкнутого контура экстремальной системы. Передаточная функция корректирующего устройства будет

165

Величина среднего отклонения от положения экстремума для экстремальной системы с двумя пробными шагами будет

где Tпр — длительность импульса пробного шага;

Т — интервал регулирования.

Для вычисления и минимизирования значения D можно воспользоваться развитой в [75] методикой Н. Винера для расчета оптимальной передаточной функции замкнутого контура экстремальной системы К(z). Чтобы посчитать оптимальную передаточную функцию К(z), необходимо знать удельные дискретные спектральные плотности помехи и внешнего возмущения, перемещающего положение точки экстремума. Обозначим их соответственно (z) и (z) .

Согласно [75], при условии, что возмущение λ и помеха δ не коррелированы

Величина К(z) определяется по формуле [21, 75]

При этом фигурные скобки выражения (2.10) означают, что берется только та часть функции (z)Y 1 , которая

имеет полюсы внутри или на круге единичного радиуса. Этим обес-

печивается устойчивость синтезируемой системы.

Найденное выражение для среднего отклонения от положения экстремума может быть использовано для определения оптимальных параметров экстремального регулятора

Пример. Пусть на экстремальную систему воздействует возмещение в виде случайного скачкообразного сигнала, среднеквадратичное значение которого равно C1 . Удельная импульсная спектральная плотность такого сигнала равна

где ν — средняя частота изменения возмущающего воздействия, определяемая через вероятность изменения

При выполнении условия устойчивости

167

Величина среднего отклонения от экстремума зависит от величины пробного шага изменения регулирующего воздействия. Существует qпр , при котором оптимальное

значение D будет минимально

q2 TC1b . (2.113)

Величина b лежит в пределах 0 < b < 1.

Используя полученные выше соотношения (2.94), (2.96)

Отсюда видно, что b определяет «степень осторожности» экстремального регулятора, при b=0 происходит полное изменение регулирующего воздействия (система «не осторожная»), при b=1 никакого изменения регулирующего воздействия не происходит.

2.3.2. Шаговая экстремальная система с модулирующим воздействием.

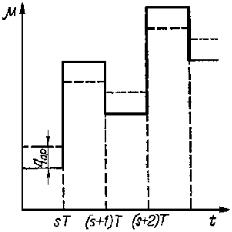
Система с модулирующим воздействием, исследованная в [75], не столько отличается от рассмотренной выше, хотя основная идея остается неизменной. Особенности этой системы можно проследить, рассмотрев рис. 2.19.

Как видно из рис. 2.19, в моменты времени sT происходит пробное изменение регулирующего воздействия

на величину ( 1)S qпр . Одновременно оценивается эффект

этих изменений на показатель качества и осуществляется рабочий шаг изменения регулирующего воздействия. Соотношения, описывающие поведение этой системы

169

j 0

Рис. 2.19. Характер изменения регулирующего воздействия в ИЭС с модуляцией.

Используя эти уравнения, можно получить

i 2aqпр ( S S ) ( 1)S S ( 1)S [ opt aqпр

Выражение в квадратных скобках можно заменить константой C2 , положив, что opt не изменяется в течение снятия

пробного сигнала C2 суммируется с помехой S . Чтобы устранить влияние C2 на работу системы, звено с передаточной функцией W (z) подключается последовательно с фильтром, передаточная функция которого будет (1 z 1 ) . Поэтому оптимальная импульсная передаточная функция

170