
Учебное пособие 1740
.pdf5. Если lim α(x)
x→a β(x)
эквивалентными б.м.
α (x) β (x) при x → a.
= 1, то α(x), β(x) называются
при x → a, что обозначается так:
Пример 1. α(x) = (1 – x)3, β (x) = 1 – x3.
Очевидно, что при x → 1 функции α(x), β(x) являются б.м. Для их сравнения найдем предел их отношения при x → 1:
lim α(x) x→1 β(x)
lim |
(1 − x)3 |
= lim |
|
(1 − x)3 |
|
= lim |
|
(1 − x)2 |
= 0 |
||||
1 − x3 |
|
− x)(1 + x + x2 ) |
|
+ x + x2 |
|||||||||
x→1 |
x→1 (1 |
|
x→11 |
|
|||||||||
Вывод: α(x) является б.м. высшего порядка, по сравне- |
|||||||||||||
нию с β(x) при x → 1. |
|
α(x) |
|
|
1 |
|
|
|
|
||||
Нетрудно убедиться, что lim |
= |
|
(убедитесь!), откуда |
||||||||||
(β(x))3 |
27 |
||||||||||||
|
|
|
|
x→1 |
|
|
|
|
|
||||
следует, что α(x) – б.м. |
3-го порядка малости, по сравнению с |
||||||||||||
β(x) при x → 1. |
|
|
|
|
|
|
|
|
|
|
|
||
Пример 2. Функции α1(x) = 4x, α2 (x) = x2, α3(x) = sinx,
α4(x) = tgx являются бесконечно малыми при x → 0. Сравним их:
lim |
α2 |
(x) |
= 0, |
lim |
α3 (x) |
= |
1 |
, |
lim |
α4 (x) |
= 1, |
lim |
α3 (x) |
= ∞. |
|
α1 (x) |
α1 (x) |
4 |
α3 (x) |
α2 (x) |
|||||||||||
x→0 |
|
x→0 |
|
|
x→0 |
|
x→0 |
|
|||||||
Отсюда заключаем, что α2(x) = x2 – б.м. высшего порядка, по
сравнению с α1(x) и α3(x) (при x → 0), α1(x) и α3(x) – б.м. одного порядка, α3(x) и α4(x) – эквивалентные б.м., т.е. sinx ~ tgx при x → 0.
31
Теорема 1. Пусть α(x) ~ α1(x), β(x) ~ β1(x) при x → a. Ес-
ли существует |
lim |
α1 (x) |
, |
|
то |
|
существует |
и |
|
lim α(x) |
, и |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
x→a β1 (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→a β(x) |
|
||||||
lim α(x) |
= lim |
α1 (x) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x→a β(x) |
x→a β1 (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
β1 (x) |
|
|
|
|
|
|
|
||||
Доказательство. |
lim |
|
α(x) |
= 1, lim |
|
= 1, |
|
|
||||||||||||||||||
|
|
|
|
|
x→a |
α1 (x) |
|
|
|
x→a |
β(x) |
|
|
|
|
|
|
|||||||||
lim |
α(x) |
= lim |
α(x) |
|
α |
1 |
(x) |
|
β |
1 |
(x) |
= |
lim |
α |
1 |
(x) |
. |
|
||||||||
|
α1 (x) |
β1 (x) |
|
|
|
|
|
|
|
|
|
|||||||||||||||
x→a β(x) |
x→a |
|
|
β(x) |
|
x→a β1 (x) |
|
|
||||||||||||||||||
Эта теорема позволяет упрощать нахождение пределов.
Пример 3. Найти lim sin 4x .
x→0
В силу первого замечательного предела sin4x ~ 4x, tg3x ~ 3x при x → 0, поэтому
lim sin 4x |
= lim |
4x |
= |
4 . |
x→0 tg 3x |
x→0 |
3x |
|
3 |
Теорема 2. Бесконечно малые функции α(x) и β(x) эквивалентны (при x → a) тогда и только тогда, когда α(x) – β(x) является б.м. высшего порядка, по сравнению с α(x) и β(x) (при x → a).
Доказательство. |
|
|
|
|
|||
Пусть α(x) ~ β(x) |
при |
x → a. Тогда |
|||||
lim |
α |
(x) − β(x) |
|
|
− |
β(x) |
|
|
α(x) |
= lim 1 |
|
= 0, |
|||
|
|
||||||
x→a |
|
|
x→a |
|
α(x) |
||
т.е. разность α(x) – β(x) – б.м. высшего порядка, по сравнению с α(x) при при x → a (аналогично с β(x)).
Пусть α(x) – β(x) – б.м. высшего порядка, по сравнению с α(x) и β(x), покажем, что α(x) ~ β(x) при x → a:
32
lim α(x) |
= lim |
(α(x) − β(x)) + β(x) |
= |
|||
|
|
|||||
x→a β(x) |
x→a |
β(x) |
|
|
||
= lim α(x) − β(x) |
+ lim |
β(x) |
= 1, |
|
||
|
|
|||||
x→a |
β(x) |
x→a β(x) |
|
|
||
т.е. α(x) ~ β(x) при |
x → a. |
|
|
|
|
|
Теорема 3. Сумма конечного числа бесконечно малых различных порядков эквивалентна слагаемому низшего порядка.
|
|
Доказательство. Пусть α(x) – б.м. низшего порядка по |
||||||||||||||||||||||
сравнению с β(x) и γ(x) при x → a, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
lim |
β(x) |
|
= 0 и |
lim |
γ (x) |
= 0. |
|
|
|
|
|
|
|
|||||||||
|
|
|
α(x) |
|
|
|
|
|
|
|||||||||||||||
|
|
x→a α(x) |
|
|
|
x→a |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Покажем, что α(x) ~ (α(x) + β(x) + γ(x)) при |
x → a: |
|
||||||||||||||||||||
lim |
α(x) + β(x) +γ (x) |
= |
lim α(x) + lim |
β(x) |
+ |
lim γ (x) |
= |
|||||||||||||||||
α(x) |
|
|
||||||||||||||||||||||
x→a |
|
|
x→a α(x) |
|
x→a α(x) |
|
x→a α(x) |
|
||||||||||||||||
|
|
|
|
=1 + 0 + 0 = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Доказанные теоремы применяются для нахождения пре- |
||||||||||||||||||||||
делов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Пример 4. Найти lim |
sin 2 |
x + 3 tg 5x + x3 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
4x + 2x3 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
По теореме 3 при x → 0: 4x + 2x3 ~ 4x , |
|
|
|
|
|
|
|
|
||||||||||||||
|
sin 2 x + 3 tg 5x + x3 |
sin2x + 3tg5x + x3 ~ 3tg5x, тогда |
|
|
||||||||||||||||||||
lim |
= |
lim |
3tg5x |
|
= |
|
3 |
|
lim |
tg 5x |
= |
15 |
. |
|
||||||||||
|
4x + 2x3 |
|
4x |
|
|
4 |
|
|
|
x |
|
4 |
|
|||||||||||
x→0 |
|
|
|
x→0 |
|
|
|
x→0 |
|
|
|
|
|
|||||||||||
33
1.10. Непрерывность функции в точке. Точки разрыва
Пусть функция f (x) определена в точке x0 и некоторой ее
окрестности. Если существует lim f (x) и |
lim f (x) = f (x0 ) , |
x→x0 |
x→x0 |
то функция f (x) называется непрерывной в точке x0, а x0 на-
зывается точкой непрерывности функции f (x).
На языке логики равенство lim f (x) = f (x0 ) описыва-
x→x0
ется формулой:
ε > 0 δ >0 x (x0 – δ, x0 + δ) |f (x) – f (x0)| < ε .
Используя понятия односторонних пределов, можно перефразировать определение так: функция называется непрерывной в точке x0, если она определена в точке x0 и некоторой
ее окрестности, если существуют lim |
f (x), |
lim f (x) и |
||
|
x→x0 −0 |
x→x0 |
+0 |
|
lim f (x) = |
lim |
f (x) = f (x0). |
|
|
x→x0 −0 |
x→x0 +0 |
|
|
|
Иногда приходится рассматривать непрерывность функции в точке x0 справа или слева. Пусть функция определена в точке x0 и некоторой ее левой полуокрестности.
Если lim f (x) = f (x0), то говорят, что f (x) непрерывна
x→x0 −0
в точке x0 слева.
Аналогично определяется непрерывность справа.
Пример 1. Функция f (x) = x3 определена на R. |
||||
Покажем, что f (x) непрерывна в точке x0 = 2. |
||||
Действительно, |
f (2) = 23 = 8, |
lim f (x) = |
lim x3 = 8, |
|
|
|
|
x→2 |
x→2 |
lim f (x) = f (2), значит, |
f (x) = x3 непрерывна в точке x0 = 2. |
|||
x→2 |
|
|
|
|
|
|
2x, |
если x ≤ 0 |
. |
Пример 2. f (x) = |
|
|||
|
|
sin x, если x > 0 |
|
|
Покажем, что f (x) непрерывна в точке x0 = 0: |
||||
f (0) = 0, lim |
f (x) = |
lim 2x = 0, lim |
f (x) = lim sinx = 0. |
|
x→0−0 |
x→0−0 |
x→0+0 |
x→0+0 |
|
34
Так как lim f (x) = lim f (x) = f (0), то непрерывность функ-
x→0−0 x→0+0
ции f (x) в точке x0 = 0 доказана. Дадим определение точек разрыва.
Пусть f (x) определена в окрестности точки x0, но может быть не определена в x0.
Точка x0 называется точкой разрыва для функции f (x), если в
точке x0 функция f (x) не определена, или lim f (x) не сущест- |
|||
|
|
x→x0 |
|
вует, или lim f (x) ≠ f (x0). |
|
|
|
x→x0 |
sin x |
|
|
Пример 3. Функция f (x) = |
не определена в точке |
||
x |
|||
|
|
||
x0 = 0, но определена в любой окрестности этой точки, поэтому
x0 |
= 0 |
является точкой разрыва для |
f (x). |
||
|
Пример 4. Функция f (x) = |
|
1 |
не определена в точке |
|
|
x −3 |
||||
|
|
|
|
||
x0 |
= 3, |
x0 = 3 – точка разрыва для f (x). |
|
||
|
Различают точки разрыва первогородаи второгорода. |
||||
Точка разрыва x0 для функции f (x) называется точкой разрыва первого рода, если существуют (конечные) пределы:
lim f (x) и |
lim f (x). В противном случае x0 – точка раз- |
x→x0 −0 |
x→x0 +0 |
рыва второго рода. В примере 4 x0 = 3 – точка разрыва второго
рода, таккак lim |
1 |
|
= –∞, |
lim |
1 |
= +∞. |
|
x − 3 |
x −3 |
||||||
x→3−0 |
|
x→3+0 |
|
||||
Точка x0 разрыва первого рода, для которой |
|||||||
|
lim |
f(x) = |
lim |
f(x), |
|||
x→x0 −0 |
|
x→x0 +0 |
|
||||
называется точкой устранимого разрыва. Такой является точка x0 в примере 3. Если рассмотреть функцию
sin x |
, если x ≠ 0 |
|
|
, |
|
ϕ(x) = x |
|
|
1, |
если x = 0 |
|
|
|
|
35
то |
ϕ(x) |
непрерывна |
в точке x0 = 0, так как |
|
lim |
ϕ(x) = |
lim |
sin x = 1 |
и ϕ(0) = 1. Доопределив функцию в |
x→0 |
x→0 |
x |
|
|
точке x0 = 0, |
мы устранили разрыв. |
|||
|
Рассмотрим операции над непрерывными функциями. |
|||
Теорема 1. Если функции f1(x) и f2(x) непрерывны в точке x0, то их сумма и произведение также непрерывны в точке
x |
. Если, кроме того, |
f (x |
) ≠ 0, то частное |
f1 |
(x) |
также непре- |
|
|
|
||||||
0 |
|
2 |
0 |
|
f2 |
(x) |
|
|
|
|
|
|
|||
рывно в точке x0.
Доказательство. Доказательство основано на свойствах пределов. Докажем, например, что сумма непрерывных функ-
ций непрерывна. Функции f1(x), |
f2(x) непрерывны в точке x0, |
||
поэтому |
lim f1(x) = f1(x0), |
lim |
f2(x) = f2(x0). Применяя теоре- |
|
x→x0 |
x→x0 |
|
му о пределе суммы двух функций, получим: |
|||
lim |
(f1(x) + f2(x)) = lim |
f1(x) + lim f2(x) = f1(x0) + f2(x0), |
|
x→x0 |
x→x0 |
|
x→x0 |
что означает непрерывность f1(x) + f2(x) в точке x0. Аналогично для других утверждений теоремы. Заметим, что формулу
lim f (x) = f (x0) (определяющую непрерывность функции f(x)
x→x0
в точке x0) можно записать в виде: lim f(x) = f( lim x), так как
x→x0 x→x0
lim x = x0. Эта формула означает, что при нахождении преде-
x→x0
ла непрерывной функции можно переходить к пределу под знаком функции.
Теорема 2. Если функция u = ϕ(x) непрерывна в точке x0, а функция y = f (u) непрерывна в точке u0 = ϕ(x0), то сложная функция y = f (ϕ(x)) непрерывна в точке x0.
Доказательство. Покажем, что lim f (ϕ (x)) = f (ϕ (x0)).
x→x0
Действительно, из непрерывности функции ϕ (x) имеем:
36

lim |
ϕ (x) = ϕ (x0) = u0, т.е. при x→ x0 следует, что u → u0. |
x→x0 |
|
Далее, из непрерывности функции f (u) получаем: |
|
lim |
f (ϕ (x)) = lim f (u) = f (u0) = f (ϕ (x0)). |
x→x0 |
u→u 0 |
Теорема доказана.
Установим непрерывность некоторых элементарных функций:
1. Всякая постоянная функция y = C непрерывна в каж-
дой точке x0 R, так как lim C = C.
x→x0
2. Функция y = x непрерывна в любой точке x0, так как
lim x = x0. Тогда функция y = Cxn, где n N, непрерывна на
x→x0
всей числовой оси, как произведение непрерывных функций.
3.Любой многочлен: y = a0 + a1x + a2x2 + ...+ anxn, непрерывен в каждой точке числовой оси, как сумма непрерывных функций.
4.Всякая рациональная дробь, являющаяся отношением
двух многочленов QP((xx)) , непрерывна во всех точках, в кото-
рых многочлен Q(x) не обращается в 0.
5. Функция y = sinx, y = cosx непрерывны в точке x0 = 0, так как
lim sinx = 0, sin0 = 0,
x→0
т.е. lim sinx = sin0
x→0
lim cosx = 1, cos0 = 1,
x→0
и lim cosx = cos0.
x→0
Сформулируем без доказательств следующую теорему. Теорема 3. Всякая элементарная функция непрерывна в
каждой точке, в которой она определена.
Если функция f (x) непрерывна в каждой точке интервала
(a, b), то говорят, что f (x) непрерывна на интервале (a, b).
37
2.ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
2.1.Понятие производной, ее геометрический
и механический смысл
Пусть функция y = f (x) определена в точке x0 и некоторой ее окрестности, x – точка из этой окрестности. Введем обозначения: разность x – x0 обозначим через x и назовем приращением аргумента, а разность f (x) – f (x0) обозначим через y и назовем приращением функции.
Итак, x = x – x0, y = f (x) – f (x0). Из равенства x = x – x0
получаем равенство x = x0 + x, тогда y = f (x0 + x) – f (x0). Производной функции f (x) в точке x0 называется предел
отношения приращения функции к приращению аргумента,
когда приращение аргумента стремится к нулю. |
|
|
|||||||
Производная обозначается f ′(x0). |
|
|
|
|
|
||||
Итак, |
y |
|
f (x0 + |
x) |
− f (x0) |
|
|
f (x) − f (x0 ) |
|
f ′(x0 ) = lim |
= lim |
= lim |
|
. |
|||||
x |
|
x |
|
|
x − x |
||||
x→0 |
x→0 |
|
|
x→x0 |
|
||||
|
|
|
|
|
|
|
|
0 |
|
Пример 1. Найти производную для функции f (x) = x2 в точке
x0 = 3.
Решение.
|
f |
′ |
= lim |
f (3 + |
x) − f (3) |
= lim |
(3 + x)2 −32 |
= |
|
|
(3) |
|
|
|
|
||||
|
|
x |
|
x |
|||||
|
|
|
x→0 |
|
|
x→0 |
|
||
= lim |
9 |
+6 x +( x)2 −9 |
= lim |
6 x +( x)2 |
|
||||
|
|
x |
|
|
x |
= lim (6 + x) = 6 . |
|||
x→0 |
|
|
|
x→0 |
|
x→0 |
|
||
Если f ′(x0) существует, то говорят, что функция f (x) диф-
ференцируема в точке x0. Установим связь между дифференцируемостью функции f (x) в точке x0 и ее непрерывностью в этой точке. Напомним, что функция f (x) непрерывна в точке x0, если она определена в точке x0 и некоторой ее окрестности, и выполняется равенство:
lim f (x) = f (x0 ) .
x→x0
38

Переформулируем это определение, используя понятия приращения аргумента и приращения функции. Из этого равенства получаем:
lim( f (x) − f (x0 )) = 0; |
lim ( f (x0 + x) − f (x0 )) = 0; |
|
|
|
x→x0 |
x→0 |
. |
(*) |
|
lim |
y = 0. |
|||
|
|
|||
x→0 |
|
|
|
Другими словами, функция f (x) непрерывна в точке x0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Теорема. Если функция f (x) дифференцируема в точке x0, то она непрерывна в этой точке.
Доказательство. Дано, что f '(x0) существует, т.е.
lim |
y |
есть некоторое число. Покажем, что выполняется |
|||||||
x→0 |
x |
|
|
|
|
|
|
|
|
равенство (*): |
|
y |
|
|
y |
|
|
||
|
|
lim |
y = lim |
|
x = lim |
|
lim x = 0 . |
||
|
|
x→0 |
x→0 |
x |
|
x→0 |
x |
|
x→0 |
Итак, доказано, что f (x) непрерывна в точке x0. Замечание. Если в точке x0 функция f (x) непрерывна, то
в этой точке функция может и не иметь производной, что подтверждается следующим примером.
Пример 2. Функция f (x) = | x | непрерывна в точке x0 = 0,
так как lim x = 0 = 0 .
x→0
Покажем, что эта функция не имеет производной в точке x0:
|
|
|
|
|
f ′(0) = |
lim |
y = |
lim |
|
|
x |
|
|
, но |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x→0 |
x |
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
|
|
1, |
если |
x > 0 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
= |
|
x < |
|
, поэтому |
lim |
|
|
|
|
|
=1, |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x |
|
|
если |
0 |
|
|
x |
|||||||||||||
|
|
|
|
−1, |
|
|
|
|
|
|
|
x→0+0 |
|
|
|
|||||||
а lim |
|
x |
|
= −1, |
значит, lim |
|
x |
|
не существует, т.е. f (x) не |
|
|
||||||||
|
x |
|
|
x |
|
||||
x→0−0 |
|
|
x→0 |
|
|
||||
дифференцируема в точке x0 = 0.
39
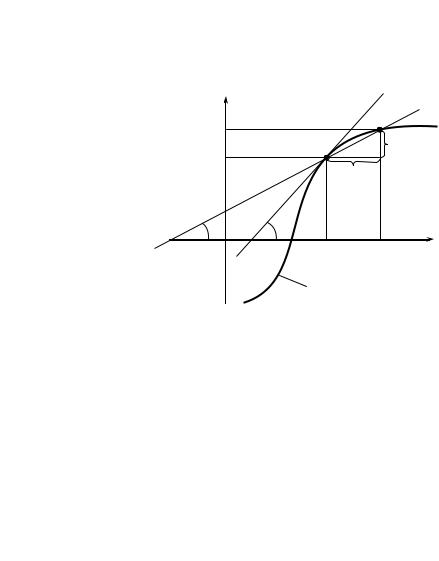
Рассмотрим геометрический смысл производной. |
|
|
|||||||||||||||
На рис. 2.1 изображен |
график |
непрерывной |
функции |
||||||||||||||
y = f (x). Точка M0 на графике имеет координаты |
x0, |
f(x0), |
|||||||||||||||
другая точка графика M – координаты |
x0 + |
x, |
|
f(x0 + |
x). |
||||||||||||
Прямая M0M явля- |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||
ется |
секущей |
для |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
||||
линии |
y = f(x), |
она |
f ( x |
|
|
+ |
x) |
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
||||||||||
наклонена к оси Ox |
|
|
|
|
|
|
M0 |
|
|
|
y |
|
|||||
|
|
|
f ( x0 ) |
|
|
|
|
|
|||||||||
под углом β. Пусть |
|
|
|
|
|
|
x |
|
A |
|
|||||||
f ′(x0) |
существует, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
т.е. |
lim |
y |
есть |
|
|
|
|
|
β |
K |
|
α |
|
|
|
|
|
|
x→0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
некоторое число. Из |
|
|
|
|
|
0 |
|
|
x0 |
x0 + |
x |
x |
|||||
M0MА получаем: |
|
|
|
|
|
|
|
||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
y = f(x) |
|
|
|
||
|
x = tgβ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(известно, что tgβ – |
|
|
|
|
|
|
|
Рис. 2.1 |
|
|
|
|
|
||||
угловой коэффици- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ент прямой M0M). Если x → 0, то точка M движется по гра- |
|||||||||||||||||
фику функции y = f (x), приближаясь к точке M0, при этом се- |
|||||||||||||||||
кущая M0M, поворачиваясь вокруг точки M0, стремится занять |
|||||||||||||||||
предельное положение, т.е. совпасть с касательной M0K, при |
|||||||||||||||||
этом β →α |
(α – угол |
между |
касательной M0K и осью Ox), |
||||||||||||||
tgβ → tgα. |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Таким образом, |
f |
′(x |
0 |
) = |
lim |
= tgα, |
но tgα = k есть |
||||||||||
|
|
|
|
|
|
|
|
|
x→0 |
x |
|
|
|
|
|
|
|
угловой коэффициент касательной M0K. |
|
к |
графику |
||||||||||||||
Итак, |
угловой |
коэффициент |
касательной |
||||||||||||||
y = f (x) в точке с абсциссой x0 равен производной функции |
|||||||||||||||||
f(x) в точке x0: f ′(x0) = k = tgα.
Вэтом состоит геометрическое истолкование производной. Очевидно, что уравнение касательной M0K имеет вид:
y – f (x0) = f ′(x0)(x – x0).
40
