
Учебное пособие 948
.pdf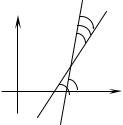
tg tg( |
1 |
|
2 |
) |
tg 2 tg 1 |
|
k2 k1 |
, (3.39) |
|
|
|||||||
|
|
1 tg 1tg 2 |
1 k1k2 |
|||||
где 1 и 2 - углы наклона прямых.
у
0 1  2 x
2 x
Рис. 14
Условие параллельности прямых определяется как случай tg 0 , т.е.
k1 k2 . |
(3.40) |
Условие перпендикулярности – это условие того, что tg
не существует, т.е. k1k2 1 0 или
k2 |
|
1 |
. |
(3.41) |
|
||||
|
|
k1 |
|
|
3.4.Кривые второго порядка
Впрямоугольной системе координат, в плоскости Oxy уравнение второй степени
Ах2 + 2Вху +Су2 +2Dх + 2Еу +F = 0 |
(3.42) |
определяет кривую второго порядка, где А, В, С, D, E, F задан-
ные действительные числа. При этом А, В, С одновременно не равны нулю.
Рассмотрим кривые второго порядка, канонические уравнения которых имеют вид:
70
|
|
x2 |
|
|
y2 |
|
|
||||||
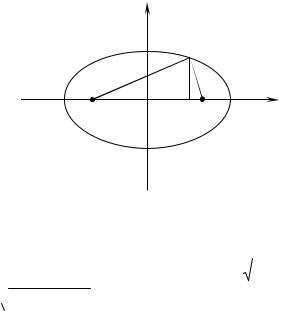
1) |
уравнение эллипса |
|
|
|
|
|
|
|
|
1, |
(3.43) |
||
a2 |
|
b2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||
частный случай которого дает уравнение окружности |
|
||||||||||||
|
x2 y2 a2 ; |
|
a 0; |
|
(3.44) |
||||||||
2) |
уравнение гиперболы |
x2 |
|
|
|
y2 |
|
1; |
(3.45) |
||||
a2 |
|
b2 |
|||||||||||
|
|
|
|
|
|
|
|||||||
3) |
уравнение параболы y2 |
2px. |
(3.46) |
||||||||||
3.4.1. Каноническое уравнение эллипса
Эллипсом называется геометрическое место точек плоскости, для каждой из которых суммы расстояний до двух фиксированных точек F1( с,о) и F2 (с,о), называемых фокусами, есть величина постоянная 2a, большая, чем расстояние между фокусами.
Y
M(x,y)
r1 r2
X
F1(-C,0) F2(C,0)
|
|
Рис. 15 |
|
|
|
Пусть расстояния от текущей точки эллипса M(x, y) |
до |
||||
|
|
|
|
||
фокусов F ( с,о) и F (с,о) |
равны r F M |
x c 2 y2 |
и |
||
1 |
2 |
1 |
1 |
|
|
r2 F2M 
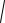 x c 2 y2 , соответственно (рис. 15).
x c 2 y2 , соответственно (рис. 15).
Тогда уравнение эллипса имеет вид
71

F1M F2M 2a или 
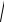 x c 2 y2
x c 2 y2 
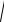 x c 2 y2 2a.
x c 2 y2 2a.
Преобразуем полученное уравнение.
2a 
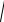 x c 2 y2
x c 2 y2 
 x c 2 y2 ;
x c 2 y2 ;
4a2 x c 2 y2 4a
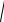 x c 2 y2 x c 2 y2; 4a2 4cx 4a
x c 2 y2 x c 2 y2; 4a2 4cx 4a
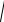 x c 2 y2 ;
x c 2 y2 ;
a4 2a2cx c2x2 a2 x2 2cx c2 y2 ; |
|
||||||
a4 a2c2 c2x2 a2x2 a2 y2 . |
|
|
|||||
Обозначая b2 a2 |
c2 , |
имеем a2b2 b2x2 a2y2 |
или |
||||
|
|
х2 |
у2 |
а b |
|
||
|
|
|
|
|
1 , |
(3.47) |
|
|
|
|
|
||||
|
|
а2 |
b2 |
|
|
||
- каноническое уравнение эллипса.
Если в уравнении заменить х на (– х), а у на (– у), то уравнение не изменится. Это значит, что эллипс - кривая симметричная относительно осей Ох и Оу.
Величины а и b называются большой и малой полуосями
эллипса, т.к. а b. Эллипс проходит через точки (0,b) и (а,0) или (0, -b) и (- а,0), которые называются вершинами эллипса. Эллипс - непрерывная замкнутая кривая, которая находится внутри прямоугольника x а; у b.
Эксцентриситетом эллипса называется величина
e |
|
с |
|
1 |
b2 |
. |
(3.48) |
|
а |
a2 |
|||||||
|
|
|
|
|
|
|||
Таким образом, |
эксцентриситет |
эллипса меньше 1, а |
||||||
эксцентриситет окружности равен 0 (т.к. b = а). Эксцентриситет эллипса можно рассматривать как меру
его «вытянутости». Если полуоси эллипса а = b (e 1) , то эллипс трансформируется в окружность радиуса R = а = b с центром в начале координат. В другом предельном случае e 0 эллипс настолько вытянут, что напоминает отрезок.
72
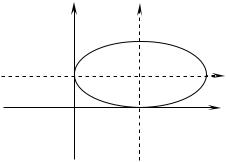
Пример 3.4.1. Привести уравнение кривой к каноническому виду и построить линию, определяемую уравнением
x2 4y2 4x 8y 4 0 .
Решение. Выделяя полные квадраты, преобразуем левую часть уравнения. Имеем
(x2 2 2x 4 4) 4(y2 2y 1 1) 4 0 ; |
|
|||
(x 2)2 4(y 1)2 4 или |
(x 2)2 |
|
(y 1)2 |
1. |
4 |
|
|||
|
1 |
|
||
Вводя новые координаты X x 2,Y y 1, получаем
X 2 |
Y2 |
|||
|
|
|
1. |
|
4 |
1 |
|||
|
|
|||
Таким образом, получено уравнение эллипса с центром в точкеО1 2;1 .
y Y
1 |
O1 |
X |
O |
2 |
x |
Рис. 16
3.4.2. Каноническое уравнение гиперболы
Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек F1( с,о) и F2 (с,о), называемых фокусами, есть величина постоянная 2a, меньшая, чем расстояние между фокусами.
73
|
Y |
|
|
|
|
M(x;y) |
|
r1 |
|
r2 |
X |
|
|
y |
|
F1(-c;0) |
0 |
x F2(c;0) |
|
Рис. 17
Согласно определению гиперболы можем записать для любой точки гиперболы M(x, y) равенство


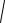 x c 2 y2
x c 2 y2 
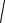 x c 2 y2 2a.
x c 2 y2 2a.
Тогда x c 2 y2 |
x c 2 y2 |
2a или |
4cx 4a2 4a
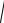 x c 2 y2 .
x c 2 y2 .
Обозначая b2 c2 a2 , имеем a2b2 b2x2 a2 y2 или
х2 |
|
у2 |
1 , |
а b |
(3.49) |
|
а2 |
b2 |
|||||
|
|
|
|
- каноническое уравнение гиперболы.
Величины a и b называются соответственно действи-
тельной и мнимой полуосями гиперболы.
Так как x и y в уравнении в четных степенях, то график гиперболы симметричен относительно координатных осей. Таким образом, гипербола обладает центром симметрии (как и эллипс).
Точки А(-а,0) и В(а, 0) называются вершины гиперболы и являются точками пересечения кривой с ось 0х. Фокусы ги-
74
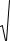
перболы располагаются на действительной оси. Гипербола не пересекается с осью Oy.
Вводится основной прямоугольник гиперболы, образован-
ный пересекающимися прямыми y b, y b, x a, x a. Диагонали основного прямоугольника гиперболы определяют-
ся уравнениями y |
b |
x и |
y |
b |
x |
|
и являются асимптотами |
||||||
|
|
|
|
||||||||||
|
a |
|
|
a |
|
|
|
|
|||||
гиперболы. |
|
|
|
|
|
|
|
|
|
||||
Эксцентриситетом гиперболы называется величина |
|||||||||||||
|
e |
с |
|
|
1 |
|
b2 |
|
. |
(3.50) |
|||
|
а |
|
2 |
||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|||
Таким образом, эксцентриситет гиперболы больше 1. Эксцентриситет гиперболы можно рассматривать как числовую характеристику величины раствора угла между её асимптотами: чем больше эксцентриситет, тем больше угол между асимптотами гиперболы.
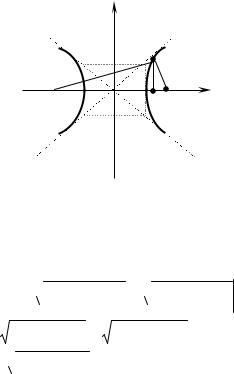
Пример 3.4.2. Привести уравнение кривой к каноническому виду и построить линию, определяемую уравнением x2 y2 6x 10 0.
Решение. Выделяя полные квадраты, преобразуем левую часть уравнения. Имеем (x2 2 3x 9 9) y2 10 0;
(x 3)2 y2 1; y2 (x 3)2 1.
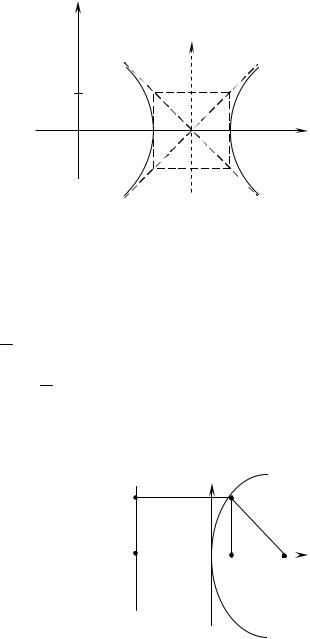
Вводя |
новые координаты X x 3,Y y , получаем |
Y2 X 2 1 - |
уравнение гиперболы, для которой действитель- |
ной осью является ось OY , а центр расположен в точке O1 3;0 .
75
y
Y
1
O1
O |
2 3 |
xX |
Рис. 18
3.4.3. Каноническое уравнение параболы
Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до точки-фокуса
F( p ,о) равно расстоянию до некоторой фиксированной пря- 2
мой y p 0 , называемой директрисой (направляющей) па- 2
раболы.
Согласно определению уравнение параболы соответствует равенству отрезков BM MF (рис. 19).
Y
d
B M(x;y)
y r
X
D p/2 x F(p/2;0)
Рис. 19
76
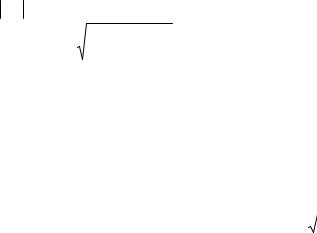
Пусть FD p, тогда
|
|
|
|
|
|
|
р |
|
2 |
|
|
2 |
|
р |
|
|
|
|
|
|
|
|
(х |
|
) |
|
у |
|
= |
|
х. |
(3.51) |
|||||
|
|
|
|
|
|
|
2 |
|||||||||||
Упрощаем: |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
p |
2 |
|
p |
|
|
|
2 |
|
|
|
|
|
|
|
|||
x |
|
|
y2 |
|
|
|
x |
|
или px y2 px. |
(3.52) |
||||||||
|
|
|
||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда получаем каноническое уравнение параболы |
||||||||||||||||||
|
|
|
|
|
y2 |
2px . |
|
|
|
(3.53) |
||||||||
Из этого уравнения видно, что парабола симметрична от- |
||||||||||||||||||
носительно оси 0х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Еe верхняя половина определяется уравнением у = |
|
|
. |
|||||||||||||||
|
2рх |
|||||||||||||||||
Точка пересечения с осью симметрии называется верши-
ной параболы. Величина р – называется параметром парабо-
лы. Если р 0, то вся парабола расположена в правой полуплоскости 0ху. Если р 0, то парабола расположена в левой полуплоскости.
Пример 3.4.3. Привести уравнение кривой к каноническому виду и построить линию, определяемую уравнением
2x2 2y |
4x 3 0. |
|
|
|
|
|
|
|
|||||
Решение. Выделяя полный квадрат, преобразуем левую |
|||||||||||||
часть |
уравнения. |
Имеем |
2(x2 2x 1 1) 2y 3 0; |
||||||||||
2(x 1)2 |
2y 5; |
y |
5 |
(x 1)2 . Вводя |
новые координаты |
||||||||
|
|||||||||||||
|
|
5 |
|
2 |
|
|
|
|
|
|
|
||
X x 1,Y y |
, |
получаем |
Y X 2 - |
уравнение параболы, |
|||||||||
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
5 |
|
|
|
||
вершина которой в точке O |
1; |
|
|
. |
|
||||||||
|
|
||||||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|||
77

y
Y
5/2 O1
X
O 1 |
x |
Рис. 20
3.5. Полярная система координат
Полярная система координат образуется полюсом-точкой О и лучом O , называемым полярной осью. Возьмем произвольную точку М на плоскости. Положение этой точки задается двумя числами, называемыми полярными координатами: полярным радиусом - расстоянием от полюса. О до точки М и полярным углом , образованным отрезком ОМ с полярной осью, при этом отсчет угла ведется от полярной оси против часовой стрелки.
Число называется полярным радиусом и может меняться на промежутке [ 0, ). Угол называется полярным углом и принимает значения на промежутке [0,2 ).
Для установления связи между прямоугольными и полярными координатами совместим полюс О с началом координат системы хОу, а полярную ось – с положительной полуосью Ох. Пусть х и у будут прямоугольными координатами точки М, а и - ее полярными координатами.
78
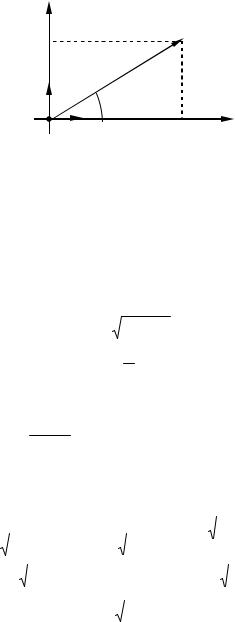
у
уМ
j |
,x |
|
|
О i |
х |
|
Рис. 21
Из рисунка видно, что прямоугольные координаты точки М связаны с полярными координатами следующим образом:
x cos , |
(3.54) |
|
|
y sin . |
|
Полярные координаты точки М выражаются через декартовые координаты формулами:
x2 y2 ,
y (3.55)
tg .
x
Пример 3.5.1. Записать в декартовых координатах уравнение линии r 3 41cos , заданной в полярной системе коорди-
нат, определить ее тип и сделать чертеж.
Решение. Воспользуемся формулами связи декартовых и полярных координат (3.54)
|
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||
cos |
|
|
|
, sin |
|
|
|
,r |
x2 y2 . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x2 y2 |
|
x2 y2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Получим |
|
x2 y2 |
|
|
|
|
|
|
|
|
или 3 x2 y2 |
4x 1. |
||||||||
|
|
4x |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x2 y2
Возведение в квадрат обеих частей дает равенство
79
