Учебное пособие 640

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Проверим жесткость балки в сечениях 1 и 2. Условия жесткости

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

507.82 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

6.2. Определение перемещений способом Верещагина Если балка состоит из прямолинейных участков с постоянной в пределах

каждого из них жесткостью, то интегралы Мора можно вычислять способом Верещагина.

Определение способом Верещагина перемещения i (прогиба или угла поворота) некоторого сечения балки ведут в следующей последовательности:

1) строят независимо друг от друга эпюру изгибающих моментов Mxp для

«грузового» состояния и эпюру изгибающих моментов Mxi для «единичного» состояния, соответствующего искомому перемещению;

2)обе эти эпюры разбивают на одинаковые участки, в пределах каждого из которых эпюра изгибающих моментов «единичного» состояния является регулярной функцией (непрерывной и не имеющей точек излома), а изгибная жесткость балки постоянна;

3)эпюру изгибающих моментов «грузового» состояния разбивают на простые фигуры (прямоугольники, треугольники и т.п.), для каждой из которых определяют площадь k и положение центра тяжести. Формулы для определения

площадей и положений центров тяжести для некоторых простейших фигур приведены в табл. 6.1;

4)под центром тяжести каждой площади ωk определяют ординату Mki на эпюре изгибающих моментов, где k-номер фигуры на эпюре «грузового» состояния; i-номер «единичного» состояния.

5)искомое перемещение определяется алгебраической суммой

m		M		ki
i	k				,	(6.2)
	EI
k 1
			x	k

где k – номер площади; m – число простейших фигур, на которые разбита эпюра изгибающих моментов “грузового” состояния. Произведение ωkMki считается положительным, если часть эпюры изгибающих моментов «грузового» состояния, имеющая площадь ωk, и соответствующая ей ордината Mki расположены по одну сторону от нулевой линии.

Положительное значение перемещения δi получается в случае, если его направление совпадает с направлением единичного силового фактора (единичной силы или момента).

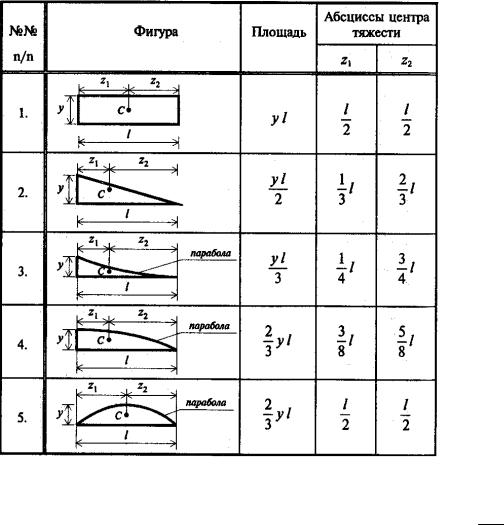
Если интенсивность q распределённой нагрузки, действующей на балку, постоянна или распределённая нагрузка отсутствует, то эпюру Mxp «грузового» состояния всегда можно разбить на площади, представленные в табл. 6.1. Для доказательства рассмотрим, например, балку, изображённую на рис. 6.2, а, эпюра изгибающих моментов которой представлена на рис. 6.2, б. Тогда выражение для изгибающего момента Mxp можно записать в виде

			z		q		2		b		b2
M	xp	m P z qz		m Pz		z		2		z
M		m P z qz		m Pz		z		2		z
		2		2					2		4
		2		2					2		4

	qb		qb2		qb		q		b	2
		z		m P		z		z

2		8			2		2		2

1 2 3

равномерно распределённой нагрузки интенсивностью q всегда равна qb2

f1(z) f2(z) f3(z),

где f1(z) m const

(площадь 1 – прямоугольник, см. рис. 6.2, в);

f2 (z) P

(площадь 2 – прямоугольный треугольник, см. рис. 6.2, г);

qb2

f3(z)

(площадь 3 – симметричный параболический сегмент, см. рис. 6.2, д).

Таблица 6.1

При этом высота h параболического сегмента (см. табл. 6.1) в случае

. Таким

образом, площадь ω эпюры изгибающего момента Mxp равна

(площадь 3 параболического сегмента отрицательна, если распределённая нагрузка направлена вверх, см. рис. 6.2, д, и положительна, если распределённая нагрузка направлена вниз).

6.3. Расчет на жесткость при изгибе Расчет на жесткость при изгибе балок выполняют исходя из условий

жесткости:

ymax y , max ,

где [y] – допускаемое значение прогиба, [y]=(0,001-0,003)ℓ. (Здесь ℓ - длина балки), [θ] – допускаемое значение угла поворота сечения ([θ]= (0,001-0,003) рад).

P	q
				a)
m	z
m	b		qb2
	b		qb2
		m Pb		2
y	Mxp			2
y	Mxp
m				б)
m
	f1(z)	z
m	f1(z)
m		1
		1		в)
				в)
		z	qb2
	f2(z)	Pb	qb2
	f2(z)	Pb	2
		3	2	г)
		z
	3	qb2
	3	8
		z		д)
		f3(z)
		Рис. 6.2

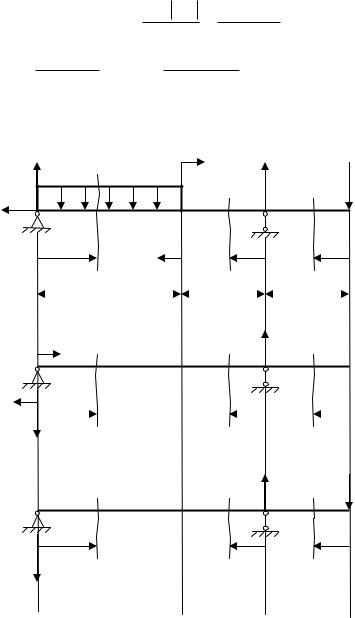
Задача 6.1

(Расчет на прочность и жесткость двуопорной балки (задача № 6 КР №2))

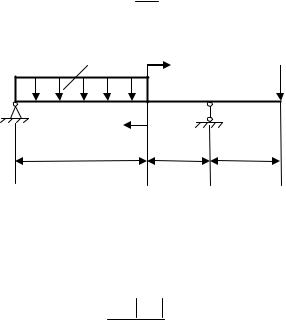
Для заданной стальной двуопорной балки постоянной жесткости (рис. 6.3) подобрать из расчета на прочность поперечное сечение в форме двутавра.

Определить методом Мора и проверить способом Верещагина угол поворота Θ опорного сечения 1 и прогиб у крайнего сечения 2 на консольном участке балки.

Проверить жесткость балки в указных сечениях, если допускаемые значения угла поворота и прогиба соответственно равны 0,02рад; y 0,002 l, где l – длина балки. Если жесткость балки не обеспечена, подобрать размер прокатного двутавра из расчета на жесткость.

Используя рассчитанные значения перемещений и эпюру изгибающих моментов, изобразить вид изогнутой оси балки.

Исходные	данные:	a 1м;	q 10 кН ;		P qa 10кН;		m 3qa2	30кНм;
160МПа; E 2 105 МПа.			м
160МПа; E 2 105 МПа.
			q	m		P
						P
	А	1			B	2
	А				B
			4а	2а		2а
			Рис. 6.3

Решение Так как жесткость балки постоянна, то из условия прочности проектный

расчет ведется по соотношению

Wx	maxM	x .	(6.3)

Для определения изгибающего момента в опасном сечении балки построим эпюры поперечной силы Qy и изгибающего момента Mx .

Определим реакции Rz , RA и RB шарнирных опор А и В (рис. 6.4, а). Реакция Rz 0 , так как горизонтальные и наклонные силы отсутствуют. Для определения RA и RB запишем уравнения равновесия:

mA	P 8a	RB 6a m 8qa2 0;	RB (8qa2 3qa2 8qa2 )/ 6a 3,17qa 31,7кН;
mB	P 2a	m 16qa2 RA 6a 0;	RA (16qa2 3qa2 2qa2 )/ 6a 1,83qa 18,3кН;

Проверка: y RA 4qa RB P 18,3 40 31,7 10 0.

Разбиваем балку по длине на три участка (см. рис. 6.4, а) и на каждом участке методом сечений определяем поперечные силы Qy и изгибающие

моменты Mx .

Участок 1: 0 z1 4a;

Q(y1) RA qz1

1,83qa qz1 ;

Qy(0) 1,83qa

18,3кН;

Qy(4a) RA q 4a

2,17qa 21,7кН.

Поперечная сила

меняет знак на участке. Определим экстремальное

значение изгибающего

момента

Mx .

Находим величину координаты z1 , при

которой Q(1)0 из уравнения

Q(1) R

qz*

0. Тогда z

* 1,83a.

Mx(1)

RAz1

qz12

1,83qaz1

qz12

;

Mx(1)(0) 0;

Mx(1)(4a) 7,34qa2

8qa2 0,66qa2

6,6кНм;

Mx(1)(z*1 ) M(x1)(1,83a) 1,67qa2 16,7кНм.

Участок 2: 0 z2 2a;

113

а)

1,83

б)

2,17

2,34

2,17

1,67

в)

0,66qa

г)

точки

перегиба

Q(y

2 ) P RB

Рис. 6.4

qa 3,17qa 2,17qa 21,7кН;

M x( 2) P( 2a z2 ) RBz2

2qa2

qaz2

3,17qaz2 2,17qaz2 2qa2;

Mx(2 )(0) 2qa2

20кНм;

Mx(2)(2a) 2,34qa2

23,4кНм.

Участок 3: 0 z3 2a;

Q(y

3 ) P qa 10кН ;

Mx(3)

Pz3 qaz3 ; Mx(3) (0) 0;

Mx(3) (2a) 2qa2 20кНм.

Строим эпюры Qy (рис. 6.4, б) и Mx

(рис. 6.4, в) и устанавливаем значение

изгибающего момента в опасном сечении балки max M x

2,34qa2

23,4кНм.

Из условия (6.6) определяем необходимое значение момента сопротивления

сечения

maxMx

23,4 106

147,5 10

мм

147,5см

160

По таблице характеристик двутавров выбираем двутавр № 18, у которого
Wx(18 ) 143см3 . Поскольку Wx(18) 147,5см3 , нужно оценить перегрузку
		maxMx				23,4 106
		max	Wx(18 )				163,6МПа;
	max		Wx(18 )			143 103
	max			163,6 160
		100%		160			100% 2,25% 5%,
что допустимо. Таким образом, окончательно выбираем двутавр № 18, у которого
Wx 143см3; Ix 1290см4 .
	RA	q			m		RB		P
	RA	q				2	RB		P
1						2			“P”	a)
1
Rz	А						B
Rz	А						B
	z1						z2	z3
		4a				2a		2a
	1						R(1)
	1						B	2		б)
A	1						B	2	“1”	б)
A	1						B
R(1)	z1						z2	z3
A
							R(2)		1
							B		1
A 1							B	2	“2”	в)
	z1						z2	z3
	RA(2)
					Рис. 6.5
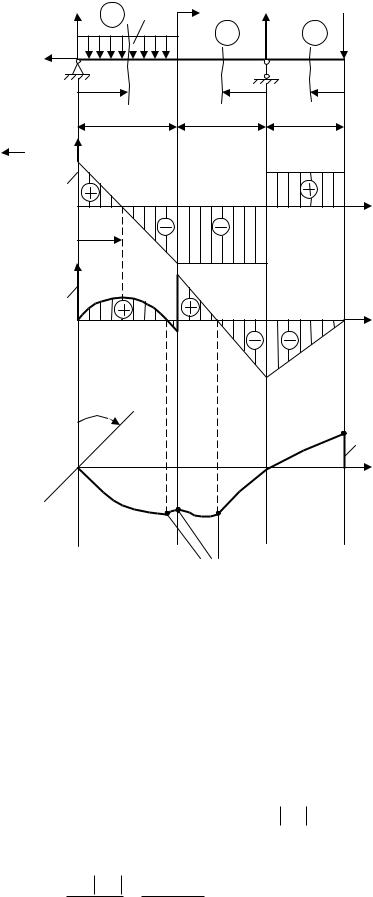
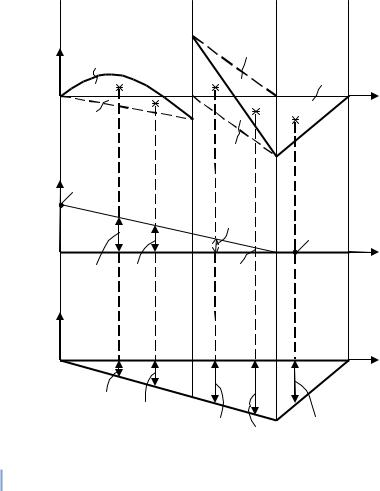
Определим угол поворота сечения 1 и прогиб у сечения 2.
Воспользуемся методом Мора. Для этого под заданной балкой, то есть под
«грузовым» состоянием “P” (рис. 6.5, а) изображаем две вспомогательные
системы или два «единичных» состояния “1” и “2” (см. рис. 6.5, б, в).
Состояние “2”


mA RB(2 ) 6a 1 8a 0; RB( 2 )			4		;	mB	R(A2 ) 6a 1 2a 0; R(A2 )	1	.

		3					3
Проверка: y RA( 2 ) RB( 2 ) 1	1			4		1 0.

3		3

Разбиваем «грузовое» и «единичные» состояния на три участка (участки «грузового» и соответствующего «единичного» состояний должны быть

одинаковой длины и рассматриваться с одной стороны см. рис. 6.5, а, б, в).

Для каждого участка составляем аналитические выражения изгибающих

моментов

M xp(k)

«грузового»

Mx(1k) ,

Mx(k2)

соответствующих

«единичных»

состояний (k = 1, 2, 3). Эти выражения представлены в табл. 6.2.

По формуле (6.1) определяем угол поворота и прогиб y :

(k )

(1)

(2)

(2)sz

(3)

Mxp

Mx1

(1)

Mxp

Mx1 dz

Mxp

Mx1

Mxp

Mx1

(EI

)

k 1lk

x k

qz1

2,17qaz2 2qa

dz qaz3 0 dz

1,83qaz1

3,1qa3

3,1 10 109

0,012рад.

EIx

2 10

1290 104

Таблица 6.2

Границы

0 z1 4a

0 z2 2a

0 z3 2a

участков

MxP(k )

1,83qaz1

qz12

2,17qaz2 2qa2

qaz3

M(k )

Mx2(k )

2 (2a z2 )

(k )

(1)

(2)

(3)

Mxp

Mx2

(2)

Mxp

Mx2 dz

Mxp

Mx2

Mxp

Mx2

(EI

)

k 1lk

x k

qz2

1,83qaz1

2,17qaz2 2qa2

qaz3 z3 dz

0,22qa4

0,22 10 1012

0,85мм.

EIx

2 105 1290 104

Проверим результаты расчета перемещений способом Верещагина. Для этого необходимо построить эпюры изгибающих моментов «грузового» “P” и «единичных» “1”, “2” состояний. Эти эпюры приведены на рис. 6.5, а, б, в соответственно. Эпюра Mxp была построена ранее при выполнении проектного

расчета на прочность (см. рис. 6.4 в). Для построения эпюр Mx1 и Mx2 использованы соответствующие выражения из табл. 6.2.

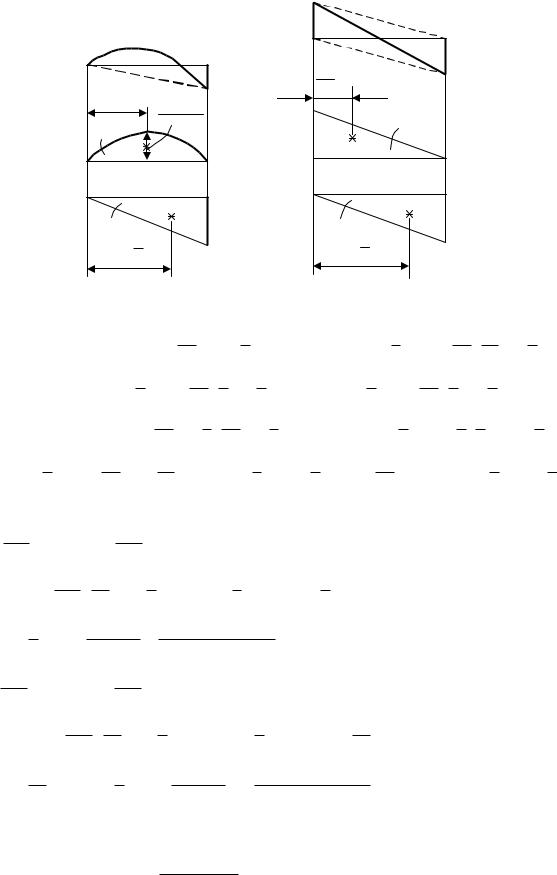
Разбиваем эпюры Mxp ,

C''

2,34qa

M x1

и Mx2

на участки

Mxp

одинаковой длины. На

каждом из этих участков

эпюру Mxp разбиваем на

простые фигуры (см. рис. 6.6,

0, 66qa2

а), для каждой из которых

можно определить площадь и

2 qa

положение центра тяжести

(см. рис. 6.3).

Mx1

M31

M51

На участке АС (см. рис.

б)

6.6,

а)

эпюра

«грузового»

M11

M21

M41

состояния

представляет

собой

несимметричный

параболический сегмент (рис.

Mx2

6.6, а). Соединив точки А и С

в)

прямой

линией,

представим

эпюру

сочетанием

двух

M12

M22

простых фигур – симмет-

M32

M52

ричного

параболического

M42

сегмента

высотой

q(4a)2

/ 8

Рис. 6.6

(см. рис. 6.7, б), площадь 1

которого

положительна,

прямоугольного

треугольника (см. рис. 6.7, в), площадь 2 которого отрицательна.

На участке СВ (см. рис. 6.6, а) эпюра «грузового» состояния представляет собой прямую, пересекающую в некоторой точке нулевую линию (рис. 6.8, а). Чтобы не определять положения точки пересечения этой прямой с нулевой линией, поступают следующим образом. Соединяют прямыми линиями точки С''

и В, а также точки С и B' (см. рис. 6.8,											а), и представляют эпюру Mxp на этом
участке совокупностью двух простых фигур: треугольника C''BC (см. рис. 6.8, б),
площадь которого 3 положительна, и треугольника CBB' (см. рис. 6.8, в),
площадь 4 которого				отрицательна. Вычисляем площади полученных простых
фигур.
		1	2	q(4a)2	4a		16	qa3 ;			2		1	0,66qa2	4a 1,32qa3 ;
				8
3						3						2
3	1	2,34qa2 2a 2,34qa3;				4			1	2qa2		2a 2qa3 ;			5	1	2qa2 2a 2qa3 .

2						2									2
Под центром тяжести площади k											каждой из фигур определяем значения
моментов Mk1 и Mk2				на соответствующих								эпюрах M x1 и Mx2 «единичных»
состояний (см. рис. 6.8, б, в).

																									C''
																									C												B
																									C													а)
					A														C						zc 2a													а)
					A														C			а)			zc 2a												B'
							z1c 2a q(4a)2 С'															а)			3				3
																													3
																									С''										3
						1											8								С''

																																					B б)
					A														C			б)			С												B б)
					A														C			в)			С												B
								2														в)																в)
												2																										в)
												2			4a				C'											c4		2	2a				B'
							zc								4a				C'										z4			3	2a				B'
									2			3																				3
												Рис. 6.7																			Рис. 6.8
	M			(1)		(2a 2a)											1	4a				2							(1)			2a			1		1		10	a	5	;
	M	11 RB				(2a 2a)											6a	4a				3		; M21 RB								2a			3	4a			3	a	9	;
																	6a					3													3		6a		3		9
				M31 RB(1) 2 2a 1 4 a 2 ; M																						41 RB(1) 1 2a 1 2 a 1 ;
													3				6a			3				9								3				6a	3		9
M51 0. M12						RA(3 ) 4a 1 4a 2 a; M																							22 R(A3) 2 4a 1 2 4a 8 a;
																2		3			2				3										3		3	3			9
M32			1					2a								14	a; M42							1				2	2a					16	a; M52				2	2a		4	a.
M32				4a												9	a; M42								4a			3	2a					9	a; M52		1			2a			a.
			3						3							9								3				3						9					3			3
По формуле (6.2) определяем угол поворота и прогиб y .
1		5						1 1M11 2M21 3M31 4M41
1		k Mk1						1 1M11 2M21 3M31 4M41
EIx k 1									EIx
5M51				1		16					3				2	1,32qa				3	5		2,34qa				3		2
5M51						3			qa						3	1,32qa							2,34qa
				EIx		3									3						9								9
2qa	3	1			3,12qa							3					3,12 10 109								0,012рад.
2qa		9		0				EIx								2 105									0,012рад.
		9						EIx								2 105		1290 104
y 1		5						1 1M12 2M22 3M32 4M42
y 1		k Mk2						1 1M12 2M22 3M32 4M42
EIx		k 1							EIx
5M52					1	16				qa				3		2						3		8	a 2,34qa					3	14		a
5M52									3	qa						a 1,32qa								9	a 2,34qa							9	a
				EIx					3							3								9								9
2qa	3	16					3		4							0,21qa4									0,21 10 1012									0,814мм.
2qa		9	a 2qa							a							EIx							2 105		1290 104								0,814мм.
		9							3								EIx							2 105		1290 104
Относительная погрешность расчета прогиба																															y	методом Мора и способом
Верещагина составляет

0,85 0,814 100% 4,2% 5%. 0,85

Таким образом, точность расчета перемещений вполне приемлема. Знаки полученных перемещений говорят о том, что сечение 1 поворачивается по ходу часовой стрелки, а сечение 2 перемещается вверх.

Длина балки l 8a 8м. По результатам расчетов перемещений

0,012рад 0,02рад, y 0,85мм y 0,002 l 16мм

Таким образом, условия жесткости выполнены.

Используя рассчитанные значения перемещений (сечение 1 поворачивается по ходу часовой стрелки, сечение 2 перемещается вверх), а также эпюру изгибающих моментов (см. рис. 6.4, в), изобразим вид изогнутой оси балки. При этом следует иметь в виду, что на тех участках, где изгибающий момент положителен, изогнутая ось обращена выпуклостью вниз. Если же изгибающий момент отрицателен, изогнутая ось обращена выпуклостью вверх. В точках, где эпюра изгибающего момента меняет знак, на изогнутой оси имеют место точки перегиба. Изогнутая ось балки изображена на рис. 6.4, г.

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022505.57 Кб4Учебное пособие 636.pdf
#
30.04.2022506.07 Кб2Учебное пособие 637.pdf
#
30.04.2022506.74 Кб3Учебное пособие 638.pdf
#
30.04.2022507.34 Кб2Учебное пособие 639.pdf
#
30.04.2022254.03 Кб5Учебное пособие 64.pdf
#
30.04.2022507.82 Кб2Учебное пособие 640.pdf
#
30.04.2022509.71 Кб5Учебное пособие 641.pdf
#
30.04.2022510.16 Кб7Учебное пособие 642.pdf
#
30.04.2022510.55 Кб4Учебное пособие 643.pdf
#
30.04.2022511.19 Кб5Учебное пособие 644.pdf
#
30.04.2022511.46 Кб2Учебное пособие 645.pdf