
Методическое пособие 694
.pdf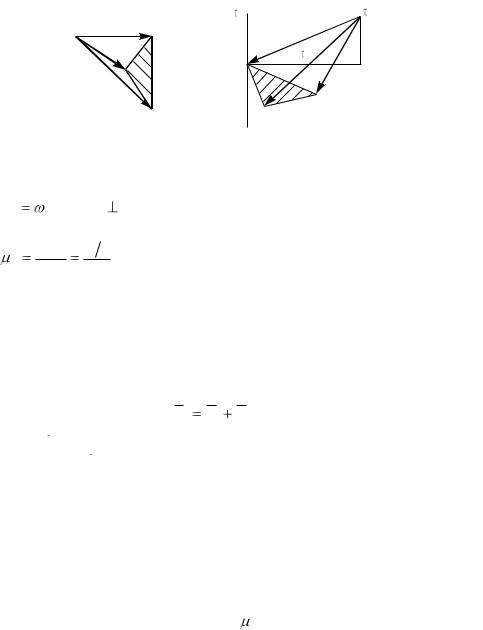
|
Приступим к построению плана скоростей (рис. 2.6). |
||||||||||
|
|
P |
|
|
C |
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
B12 |
n |
K |
|
b12 |
|
|
|
|
|
|
|
|
c |
|
|
|
||
|
|
|
а |
|
|
|
|
б |
|
|
|
|
|
|
|
|
Рис. 2.6 |
|
|
|
|
||
|
1. |
Определяем |
скорость |
точки |
В |
ведущего |
звена: |
||||
VB |
1 AB , |
VB |
AB . |
|
|
|
|
|
|
||
|
2. |
Выбрав |
полюс плана |
Р, |
откладываем в масштабе |
||||||
V |
VB |
|
м с |
вектор скорости точки В VB (рис. 2.6, а). |
|||||||
PB12 |
мм |
||||||||||
|
|
|
|
|
|
|
|
||||
3. Переходим к определению скорости точки С. Точка С принадлежит звену ВС и СD. Звено ВС совершает плоскопараллельное движение. Скорость точки С определяется по теореме сложения скоростей – скорость любой точки звена, совершающего сложное движение, определяется как сумма скоростей в переносном и относительном движении, т.е.
VC VB VCB .
VB является переносной скоростью в поступательном движении, VBC – относительная скорость во вращательном движении точки С вокруг точки В (направлена перпендикулярно к СВ).
Строим на плане это направление: через точку в проводим линию перпендикулярную к ВС. Из полюса проводим направление скорости точки С при ее движении вокруг D. Точка пересечения двух направлении дает положение точки С на плане. Скорость точки С определяется как
VC=(РС) V.
V.
39
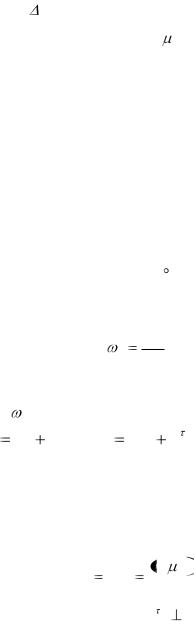
Чтобы найти скорость точки К, необходимо на векторе B12C построить вкс и сходственно с ним расположенное
Vк=(РK) V.
V.
Это свойство плана скоростей носит название теоремы подобия скоростей.
2.1.6.Свойство планов скоростей
1.План скоростей – это плоский пучок лучей, исходящих из полюса. Каждый луч представляет собой вектор абсолютной скорости какой-то точки механизма.
2.Отрезки, соединяющие концы векторов, являются относительными скоростями.
3.Свойство подобия: фигуры, образованные на полюсе векторами скоростей, подобны фигурам, образованным звень-
ями механизма, повѐрнутыми на 90 .
4. Возможность определения угловой скорости звеньев по величине и направлению:
VCB .
2
CB
План ускорений (рис. 2.6, б):
1)aBn  12 AB ;
12 AB ;
2)aC aB aCB ; aCB aCBn aCB .
Ускорение точки звена, совершающего сложное движение, складывается из переносного ускорения и относительного нормального и касательного. В данном случае переносное ускорение по характеру поступательное, а относительное вращательное.
an |
V 2 |
|
c |
B V |
2 |
|
CB |
|
|
|
; |
||
CB |
CB |
|
|
CB |
|
|
|
|
|
|
|
||
aCB || CB; |
aCB |
CB. |
||||
40

Второе уравнение:
a |
a |
a n |
a |
|
; |
|||
C |
D |
|
CD |
CD |
|
|
||
a n |
V 2 |
|
CD |
V |
2 |
|
|
|
CB |
|
|
|
|
|
; |
||
CD |
CB |
|
CB |
|
|
|
||
|
|
|
|
|
||||
aCD ||CD; |
|
aCD |
|
CD. |
||||
Построим план ускорений по приведенным векторным уравнениям, найдем ускорение точки К по аналогичным уравнениям.
Свойства плана ускорений.
1–3. Эти свойства аналогичны свойствам плана скоростей.
4. Угловую скорость второго звена можно определить
2aCB .CB
2.1.7.Построение плана скоростей и ускорений кулисного механизма (рис. 2.7)
D 4
E 5
1 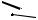 2
2
B
А 
 3
3
C
Рис. 2.7
41
Дано: |
1 = const, размеры звеньев. |
|
|
|
|
|
|
||
Определить скорости и ускорения всех точек механизма. |
|||||||||
Механизм содержит подвижных звеньев n=5; кинемати- |
|||||||||
ческих пар 5-го класса P5=7; степень подвижности W=1, класс |
|||||||||
механизма – 2 (рис. 2.8). |
|
|
|
|
|
|
|||
|
D |
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
B2 |
|
|
|
|
|
|
||
|
B3 |
|
|
|
|
|
|
||
|
D |
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
B1 |
|
E |
5 |
|
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
А |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
C
Рис. 2.8. Структура кулисного механизма Точка В1 совершает вращательное движение вокруг точки А
VB1= 1 AB ;
точка В3 совершает вращательное движение вокруг точки С; точка В2 совершает сложное движение – переносное вращательное вместе с точкой В3 и относительное поступательное вдоль звена СД:
VB2 VB3 VB2 B3 ; VB2 VB1 .
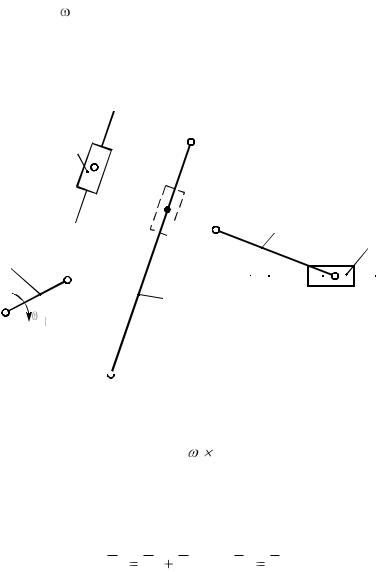
Построим план скоростей (рис. 2.9).
42
P e
b3 |
d |
|
b12
Рис. 2.9
Скорость точки D находим исходя из свойства подобия:
CD |
|
Pd3 |
; Pd |
|
|
|
|
Pb3 CD |
; Vd |
|
Vd |
|
. |
||||||
|
|
3 |
|
|
|
3 |
4 |
||||||||||||
CB |
|
Pb3 |
|
|
|
|
CB |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
VE |
|
VD |
VE D |
|
|
|
|
|||||||||
|
5 |
|
3 |
5 |
3 |
|
|
|
|
|
|||||||||
VE5 VE0 VE5E0 .
VE0 0
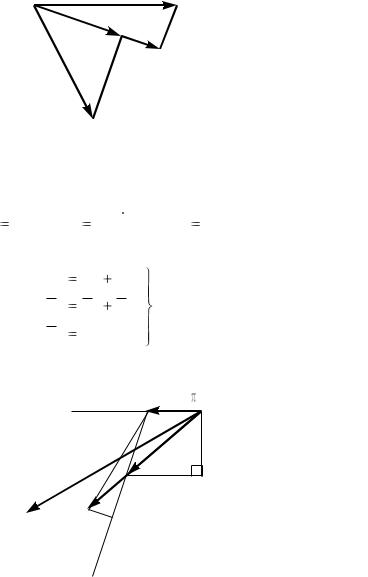
Переходим к плану ускорений (рис. 2.10).
e |
b3 |
b12 
d
Рис. 2.10
43
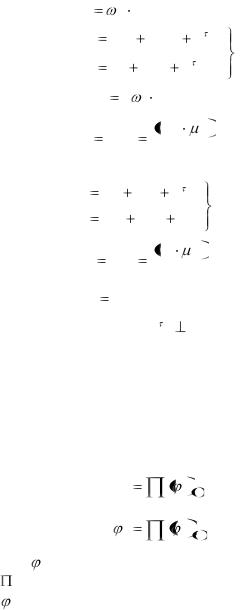
an |
|
|
|
|
2 |
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
B |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
aB |
|
|
aB |
|
|
aBk |
B |
|
|
aB B |
звено 3; |
|||||||||||||
a |
3 |
|
|
a |
12 |
|
|
a n |
12 |
3 |
a |
|
|
12 3 |
||||||||||
B |
|
|
|
|
|
|
|
|
B C |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
C |
|
|
B C |
|
|
|
|
|
|
|
|
|||||||
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|||
a k |
B |
|
|
2 |
|
|
3 |
V |
B |
B |
; |
|
|
|
|
|
|
|||||||
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
12 |
3 |
|
|
|
|
|
|
|
|
|
an |
VB2 C |
|
|
|
|
Pb |
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
3 V |
|
|
; |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
B |
|
BC |
|
|
|
|
|
|
BC |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
aE |
aD |
|
|
aEDn |
|
|
aED |
|
|
звено 4 |
||||||||||||||
a |
E |
a |
E |
|
|
|
a k |
|
|
|
a r |
|
|
звено 5; |
||||||||||
|
|
|
|
0 |
|
|
|
EE |
0 |
|
|
|
EE |
0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
an |
|
V |
2 |
|
|
|
ed |
|
|
V |
|
2 |
|
|
|
|
||||||||
|
|
|
|
ED |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|||||
|
ED |
|
|
ED |
|
|
|
|
|
|
ED |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a k |
|
|
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
EE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
|| ED; |
|
|
a |
ED |
|
|
|
ED; |
a r |
|| xx. |
|||||||||||||
|
ED |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EE0 |
||||
2.1.8. Аналоги скоростей и ускорений
Если степень свободы механизма равна единице, то положение выходного звена однозначно определяется обобщенной координатой или углом поворота входного (ведущего) звена. Запишем для первого и второго механизма (рис. 2.11):
Sn |
1 |
1 |
; |
(2.15) |
n |
1 |
2 |
, |
(2.16) |
где Sn и n – положение выходного звена;
– функция положения; 1 – положение входного звена.
44
а |
б |
Рис. 2.11
Чтобы определить линейную и угловую скорости выходных звеньев, достаточно продифференцировать выражения
(2.15) и (2.16) по времени:
|
S |
dSn |
|
|
d |
|
1 |
|
|
d |
|
1 |
|
d 1 |
|
' |
|
; |
(2.17) |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||
|
n |
dt |
|
|
dt |
|
|
|
|
d |
|
|
|
dt |
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
n |
|
d |
n |
|
|
d |
1 |
|
|
|
d |
|
1 |
|
d 1 |
' |
|
1 . |
(2.18) |
|||
|
dt |
|
|
dt |
|
|
|
|
d |
|
|
|
|
dt |
|
1 |
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
В выражениях (2.17) и (2.18) структура правых частей одинакова, т.е. линейная или угловая скорость выходного звена определяется угловой скоростью 1 входного звена и функ-
цией |
' |
, которая называется аналогом скорости или пер- |
1 |
вой передаточной функцией. Что это такое аналог скорости?
В выражении (2.18) разделим левую и правую часть на 1 и, получим
n |
' |
|
|
1 . |
|
1 |
||
|
Аналог скорости – это отношение скоростей выходного и входного звеньев. Аналог скорости является функцией положения механизма.
45

Существуют механизмы, где |
' |
=const, например |
1 |
зубчатые передачи с круглыми колесами. Здесь аналог скоростей называется просто передаточным отношением.
|
В кулачковых механизмах при 1=const и 1 const функ- |
||
ция |
' |
|
не постоянна. Такое положение вызывает допол- |
|
1 |
||
|
|
|
|
нительные динамические нагрузки в механизмах, связанные с силами инерции, которые, в свою очередь, обусловлены ускорениями.
Продифференцируем по времени выражения (2.17) и (2.18), получим линейное ускорение
|
|
2 |
|
|
|
d |
' |
1 1 |
|
d |
' |
|
|
1 |
|
|
d |
Sn |
|
|
1 |
1 |
d |
' |
|
||||||||
Sn |
dt |
2 |
|
|
dt |
|
|
|
dt |
|
dt |
1 |
(2.19) |
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
'' |
|
|
2 |
' |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|||
и угловое ускорение
|
d 2 |
' |
2 |
' |
. |
|
1 |
1 |
|||
n |
dt2 |
1 |
1 |
||
|
|
|
|
|
2.2. Силовой анализ механизмов
Силовой анализ механизмов представляет собой решение первой задачи динамики системы: определение сил по заданному закону движения. Определению подлежат реакции в кинематических парах механизма. Для решения этой задачи в «Теории механизмов и машин» применяется метод кинетостатики. Метод кинетостатики это формальный прием, который позволяет записать уравнения движения в форме уравнений равновесия и, следовательно, решать задачу методами статики.
Заметим, что метод кинетостатики это не единственный способ решения этой задачи: можно, освобождаясь от связей, вводить реакции связей в уравнение движения системы и на-
46
ходить последние из них. Звенья механизма, находящегося в движении, в общем случае не находятся в равновесии, т.к. они движутся с ускорениями.
Однако мы можем рассматривать равновесие всего механизма и каждого звена в отдельности, если применим к решению этой задачи принцип Даламбера, который утверждает следующее: если систему, находящуюся в движении, в какой – либо момент времени мгновенно остановить и к каждой материальной точке этой системы приложить действовавшие на нее в момент остановки активные силы, реакции связей и силы инерции, то система останется в равновесии.
При определении неизвестных реакций мы будем расчленять механизм, пользуясь принципом освобождаемости от связей, т.е. будем выделять из механизма группы звеньев и отдельные звенья, рассматривать их равновесие. При этом действия отброшенных звеньев на рассматриваемые будем представлять реакциями, действующими на рассматриваемые звенья со стороны отброшенных в расчлененных кинематических парах.
2.2.1. Условие статической определимости кинематических цепей
Расчленяя механизм на части и прикладывая в расчлененных кинематических парах реакции со стороны отброшенных звеньев, следует иметь в виду, что не всякая выделенная из механизма кинематическая цепь будет статически определимой системой. Статически определимой будет такая система, в которой число неизвестных (определяемых сил) будет равно числу уравнений статики. Для плоских механизмов, в состав которых входят кинематические пары 5-го и высшие пары 4-го классов, и на которые действует плоская система сил, число неизвестных реакций связей совпадает с числом ограничений, имеющихся в этих кинематических парах. Так, например, соединение звеньев во вращательную кинематическую пару 5-го класса отнимает возможность движения центра вра-
47
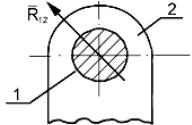
щения вдоль координатных осей за счет возникновения сил, препятствующих движению в этих направлениях.
Таким образом, определению подлежат обе проекции силы реакции на координатные оси, т.е. неизвестных будет два. Если же говорить о равнодействующей силе реакции как о векторе, то неизвестными будут величина и направление силы. Третья характеристика силы – точка ее приложения – может быть условно помещена в центр шарнира (поскольку сила – это скользящий вектор). Конечно, «точка приложения» это понятие условное, так как силы реакции распределены по поверхности соприкосновения звеньев, однако равнодействующая реакции проходит через центр шарнира (рис. 2.12).
Рис. 2.12
Соединение звеньев в поступательную пару 5-го класса отнимает свободу движения вдоль одной из координатных осей (этому движении препятствует сила, направленная вдаль этой оси) и свободу вращения вокруг оси, перпендикулярной координатной плоскости. Это говорит о том, что реакция создает момент, направленный против момента активных сил. Таким образом, в этой кинематической паре также имеются две неизвестные характеристики силы: величина и точка ее приложения. Обычно начало координат помещается в центр смежной вращательной кинематической пары, относительно оси которой могло бы совершаться вращение рассматриваемого звена
(рис. 2.13).
В высшей паре четвертого класса неизвестна только одна характеристика силы: ее величина, т.к. направление еѐ (по
48
