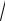Методическое пособие 601
.pdf
|
|
sАМ1(t) |
sИ(t) |
|
S0 |
|
|
|
SΩ |
|
t |
τ |
t |
|
|
|
|
T |
|
|
−SΩ |
|
|
а |
|
в |
sЧМ(t) |
|
|
|
sАМ2(t) |
|
S0 |
|
|
|
|
|
|
|
S0 |
|
t |
t |
|
|
б |
г |
|
Рис. П3.3 |
Поскольку сигнал sИ(t) обладает как положительными, так и отрицательными фиксированными значениями, частота ЧМ-сигнала f (t) будет принимать то увеличенное до fВ = f0 + KЧМ·SΩ на интервале [0, τ], то уменьшенное до fН = f0 − KЧМ·SΩ при t [τ, T−τ] постоянное значение. Переход от одного значения частоты к другому происходит скачком, так что ЧМ-сигнал приобретает вид, показанный на рис. П.3.3, б. Девиация частоты радиосигнала в соответ-
ствии с (10) будет составлять FД = max| f (t) − f0| = KЧМ·SΩ, так что fВ,Н = f0 ± FД. При определении спектрального состава колебания с угловой модуляцией
необходимо иметь в виду следующее. Если при амплитудной модуляции каждая гармоника информационного сигнала независимо от прочих порождает ровно две спектральные составляющие на выходе модулятора и результат модуляции сложным сигналом можно получить как сумму частных спектров, порождаемых отдельными компонентами информационного сигнала, то при угловой модуляции такой подход оказывается некорректным. Добавление всего одной гармоники к спектру информационного сигнала не только влечёт обогащение спектра модулированного колебания, но и перераспределение амплитуд всех наблюдавшихся ранее составляющих спектра. Таким образом, предложить универсальный аналитический способ расчёта спектральных характеристик ЧМ- и ФМсигналов, к сожалению, невозможно.
В данном случае целесообразно воспользоваться тем, что анализируемый ЧМ-сигнал может быть рассмотрен как сумма двух АМ-сигналов sАМ 1(t) и sАМ 2(t) (рис. П.3.3, в и г), подобных показанному на рис. П.3.1, в. Оба сигнала обладают периодической огибающей амплитуд, единичным коэффициентом модуляции и амплитудой несущего колебания S0/2 (на входе модулятора), но отли-
210
чаются длительностью импульсов (τ и Т − τ) и частотой заполнения: у сигнала
sАМ 1(t) частота равна fВ = f0 + FД, у sАМ 2(t) – соответственно fН = f0 − FД. Заметим, что подобное представление ЧМ-сигнала возможно далеко не всегда, а
только при условии точного фазового соответствия отрезков высокочастотных колебаний, образующих сигналы sАМ 1(t) и sАМ 2(t), непрерывным гармоническим колебаниям частоты fВ и fН соответственно. Несложно показать, что такое условие приводит к определённым ограничениям, накладываемым на девиацию частоты FД и длительность импульсов τ радиосигнала. Предлагаемый подход абсолютно справедлив, если
2FД =k FM ,
2FД =m q FM ,
где k и m – натуральные числа, q = T/τ – скважность модулирующих импульсов. Комплексные амплитуды составляющих комплексного спектра сигнала sАМ 1(t) могут быть найдены в соответствии с формулой (П.2). При подстановке
в (П.2) вместо S0 величины S0/2 и учёте запаздывания огибающей на 0,5τ, легко получить
CɺnAM1=0,5S0 τ FM sinc(π n τ FM ) exp(− jπ n τ FM ),
(П.4)
где частота n-й спектральной составляющей сигнала sАМ 1(t) равна ± f В + n FM. По аналогии комплексные амплитуды составляющих сигнала sАМ 2(t) с
импульсами длительности (Т − τ) = (1/FM − τ) и огибающей, запаздывающей на
время (Т + τ)/2 = (1/FM + τ)/2: |
|
|
|
|
|||
Cɺ |
nAM2 |
=0,5S |
(1/F −τ) F sinc[π n (1/F −τ) F |
]× |
|||
|
0 |
M |
M |
M |
M |
|
|
|
|
×exp[− jπ n (1/FM+τ) FM ], |
|
|
(П.5) |
||
где частота n-й спектральной составляющей сигнала sАМ 2(t) равна ± f Н + n FM. Итак, в спектре ЧМ-сигнала при f > 0 имеются две группы спектральных
составляющих, отличающихся положением на оси частот (одна локализована вблизи частоты fН = f0 − FД, другая – fВ = f0 + FД). Огибающая амплитуд обеих групп описывается функцией sinc( ). Поскольку ЧМ-сигнал на частоте fВ существует τ секунд, на частоте fН – остальные (T−τ) секунд, причём τ ≠ (T−τ), то в интенсивности и ширине обеих sinc-групп может наблюдаться существенная разница (рис. П.3.4). Частотный интервал между соседними спектральными со-
211

ставляющими ∆f = 1/T = FM у обеих групп один и тот же, так как его величина определяется не длительностью отдельных импульсов, а частотой модуляции. Поскольку удвоенное значение девиации частоты кратно частоте модуляции (2FД = k FM), имеет место точное совпадение частот составляющих обеих групп. Совокупное распределение амплитуд по частотам будет вырожденным и в общем случае несимметричным. Амплитуды спектральных составляющих ЧМсигнала определяются как результат удвоения модуля суммы комплексных амплитуд (П.4) и (П.5).
AnЧМ
AnАМ2 AnАМ1
0 |
f0−FД |
f0+FД f |
|
|
Рис. П.3.4 |
|
|
Результат сложения может быть записан в виде |
|
||
AnЧМ =S0 {|τ FM sinc(π n τ FM ) exp(− jπ τ n FM )+(1−τ FM )× |
|
||
×sinc[π (n+k) (1−τ FM )] exp[− jπ (n+k) (1+τ FM )]|}, |
(П.6) |
||
где n «пробегает» значения … −(5+k), −(4+k),…−k,…0, +1, +2,…; k – целое положительное число: k = 2FД / FM.
Частоты гармоник определяются выражением: f n = f 0 + FД + n FM.
П.3.1.3. Периодическая последовательность прямоугольных импульсов sИ(t) (рис. П.3.3, а) подаётся на управляющий вход идеального фазового модулятора с крутизной KФМ, рад/В. На второй вход модулятора поступает несущее гармоническое колебание с амплитудой S0 и частотой f0.
При фазовой модуляции пропорционально мгновенным значениям sИ(t) изменяется набег фазы радиосигнала: ϕ(t) = KФМ sИ(t). Поскольку мгновенные значения sИ(t) определяются константами в пределах обоих интервалов [0, τ] и [τ, T−τ] его периода, то значения набега фазы ФМ-сигнала в пределах соответствующих интервалов постоянны (рис. П.3.5, а); максимальное абсолютное значение ϕ(t) на периоде составляет KФМ·SΩ, что по определению есть индекс модуляции (m) ФМ-сигнала. По окончании интервалов постоянства происходит скачкообразное изменение набега ϕ(t) на удвоенное значение индекса: 2m = 2KФМ·SΩ. Полагая далее, что индекс модуляции m составляет точно r π/2
212
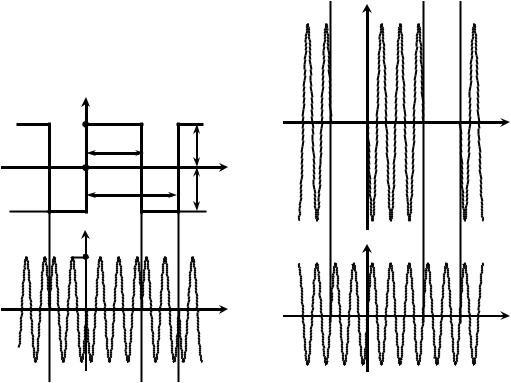
радиан (r = 1, 3, 5,…), тогда формируемое модулятором колебание в моменты времени τ ± l T и T ± l T (l – целое число) скачком меняет фазу на π радиан. Мгновенная частота рассматриваемого ФМ-колебания согласно (8) в любой произвольный момент времени постоянна и равна частоте несущей f0. Диаграмма ФМ-сигнала показана на рис. П.3.5, б.
KФМ SΩ ϕ(t)
τ
T
−KФМ SΩ
а
sФМ(t)
S0
б
s1(t)
2S0
t
m t
m
в
S0 s2(t)
t |
t |
|
г
Рис. П.3.5
Формируемое модулятором ФМ-колебание можно рассматривать как сумму двух сигналов. Первый компонент s1(t) (рис. П.3.5, в) представляет собой последовательность радиоимпульсов длительности τ удвоенной амплитуды, по сравнению с исходной S0, и фазы, одинаковой с фазой исходного ФМ-сигнала в совпадающем интервале времени. Вторым компонентом (рис. П.3.5, г) является немодулированное гармоническое колебание s2(t) с противоположной, по сравнению с первым сигналом s1(t), фазой.
Комплексные амплитуды составляющих сигнала s1(t) могут быть найдены по (П.2):
Сɺn1 = S0 τ FM sinc(π n τ FM ) exp(− jπ n τ FM ),
(П.7)
где частота n-й спектральной составляющей равна ± f 0 + n FM, n = 0, ±1, ±2, ...
Для сигнала s2(t) —
Cɺn2 =0.5S0 exp(− jπ), |
(П.8) |
213
причём составляющих в комплексном спектре всего две — с частотами ± f 0 . Таким образом, спектр анализируемого ФМ-колебания определяется так-
же суммой спектров двух сигналов s1(t) и s2(t). Описание сигнала s2(t) в частотной области очень простое, поэтому спектральные составляющие ФМ-сигнала точно соответствуют составляющим s1(t), за исключением колебания на частоте несущей. Формула для расчёта коэффициентов ряда Фурье имеет вид:
ɺ |
S0 |
τFM |
−S0 /2, n=0; |
|
CnФM = S |
τF |
sinc(πnτF ) exp(− jπnτF ), n≠0. |
||
|
0 |
M |
M |
M |
При переходе к искомому гармоническому спектру амплитуд окончательно получим
S0 |(1−2τFM )|, n=0; |
|
|
|
AnФM = 2S τF |sinc(πnτF )|, n>0. |
(П.9) |
||
0 M |
M |
||
|
|||
Заметим, что амплитуды гармоник рассмотренного ФМ-сигнала не зависят от величины индекса модуляции m, но только при условии, что m = r π/2 радиан, где r = 1, 3, 5,….
П.3.2. Спектр амплитуд сигнала, модулированного последовательностью пилообразных импульсов
П.3.2.1. Пусть на управляющий вход идеального амплитудного модулятора с крутизной KАМ подаётся периодическая последовательность sИ(t) знакопеременных пилообразных импульсов (рис. П.3.6, а, где SΩ – амплитуда, Т = 1/FM – период (FM – частота) модуляции). На второй вход модулятора подаётся несущее колебание S0 cos(2πf 0 t) амплитуды S0 и частоты f0. Огибающая амплитуд АМ-сигнала на выходе модулятора изменяется пропорционально мгновенным значениям информационного колебания sИ(t): А(t) = KАМ sИ(t) + S0 (рис. П.3.6, б, где KАМ SΩ – максимальное отклонение А(t) от амплитуды несущей, равное M S0 согласно (3), М – коэффициент модуляции). Временная диаграмма соответствующего такой огибающей амплитуд радиосигнала показана на рис. П.3.6, в.
Пилообразное колебание sИ(t) (рис. П.3.6, а) хорошо известно в теории радиотехнических сигналов; комплексные амплитуды составляющих комплексного спектра такого сигнала согласно [2] определяются выражением:
214
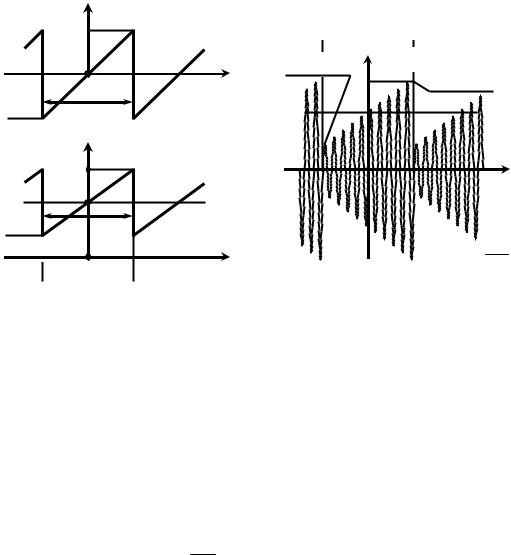
−SΩ
S0−K
sИ(t)
SΩ
|
t |
|
S0 (1−M) sАМ(t) |
S0 (1+M) |
|
|
T |
|
|
||
|
|
S0 |
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
A(t) |
|
|
|
t |
|
S0+KАМ SΩ |
|
|
|
|
|
|
|
|
|
|
S0 |
|
|
|
|
|
S |
1/FM |
|
|
|
|
t |
|
|
M=KАМ |
SΩ |
|
|
б |
|
в |
S0 |
|
|
|
|
|||
|
Рис. П.3.6 |
|
|
||
|
0 при n=0, |
|
|
||
|
CɺnИ = |
n |
π/2 /(nπ) при n≠0. |
|
|
|
SΩ e j(−1) |
|
|
|
|
где f n = n FM – частота n-й составляющей. Используя это выражение, можно найти амплитуды составляющих комплексного спектра огибающей амплитуд радиосигнала. Из рис. П.3.6, б следует, что мгновенные значения огибающей А(t) отличаются от мгновенных значений sИ(t) в KАМ раз; кроме того в составе огибающей есть постоянная составляющая величины S0. Тогда
S при n=0,
ɺ = 0
CnA S0 M e j(−1)n π/2 при n≠0.
nπ
Комплексные амплитуды составляющих АМ-сигнала определяются на основе комплексного спектра огибающей по теореме смещения спектра, в соответствии с которой
S |
0 |
/2 при n=0, |
|
CɺnAM = |
|
± jπ/2 |
|
S0 M e |
/(2nπ) при n≠0, |
||
где n-я составляющей имеет частоту f n = ± f 0 + n FM.
При переходе к амплитудам гармоник легко получить выражение для гармонического спектра амплитуд АМ-сигнала:
S |
|
при n=0, |
(П.10) |
AnAM = |
0 |
M /(nπ) при n>0. |
|
S0 |
|
||
215
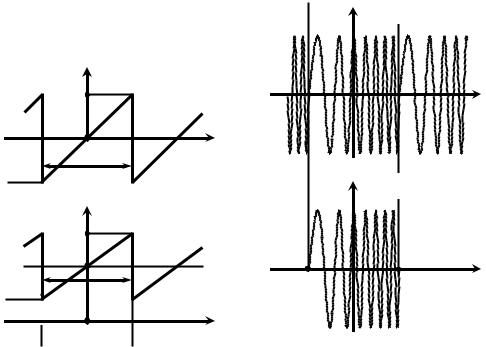
П.3.2.2. Периодическая последовательность sИ(t) пилообразных импульсов (рис. П.3.7, а) поступает на управляющий вход идеального частотного модулятора с крутизной KЧМ, Гц/В. На второй вход модулятора подаётся несущее гармоническое колебание S0 cos(2π f 0 t + ψ0) амплитуды S0 и частоты f0.
−SΩ
f0−K
|
sЧМ(t) |
|
|
S0 |
|
sИ(t) |
t |
|
SΩ |
||
|
||
|
t |
|
T |
в |
|
|
||
а |
s'ЧМ(t) |
|
f(t) |
S0 |
|
|
|
f0+KЧМ SΩ |
|
f0 |
T/2 |
t |
1/FM |
−T/2 |
|
t |
|
|
S |
|
|
б |
г |
|
|
Рис. П.3.7 |
|
Мгновенная частота ЧМ-колебания согласно (4) линейно нарастает в пределах периода информационного сигнала sИ(t) (рис. П.3.7, б) от минимального значения, равного fН = f0 − FД, до максимального значения, составляющего fВ = f0 + FД соответственно, где FД = KЧМ·SΩ – девиация частоты ЧМ-колебания. Соответствующий ЧМ-сигнал показан на рис. П.3.7, в.
Будем считать, что ЧМ-сигнал является периодическим – на периоде модуляции 1/FM укладывается точно k периодов колебания с изменяющейся частотой. При таком условии поиск спектра sЧМ(t) может быть сведён к расчёту спектральной плотности одиночного импульса s'ЧМ(t) с линейно изменяющейся частотой (рис. П.3.7, г).
Мгновенная частота радиоимпульса s'ЧМ(t) в пределах его длительности (t [−T/2, T/2]) определяется выражением
f (t)= f0 +2SΩKЧМ t/T = f0 +2FД FМ t,
мгновенные значения сигнала – s'ЧМ(t) = S0 cosΨ(t), где Ψ(t) – полная текущая фаза, определяемая интегралом от f(t):
t
Ψ(t)=2π ∫ f (t)dt +ψ0 =2π ( f0 t+FД FМ t2 )+π ( f0 −FД /2)T+ψ0.
−T/2
216