
Методическое пособие 551
.pdf
вующее координате :
Учитывая, что |
, по- |
следнее уравнение можно переписать следующим образом |
|
Кроме момента импульса, в данной задаче мы можем использовать еще один интеграл движения – полную энергию системы:
Выразим из уравнения (7.8) и исключим с помощью (7.4):
Разделяя переменные и интегрируя, получим
где – значение координаты в начальный момент времени
.
Далее, перепишем (7.4) в виде
81

Подставляя в это выражение |
из соотношения (7.8) и |
||||||
интегрируя, получим |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
– значение угла в момент времени |
. |
|
Итак, мы получили решение рассматриваемой задачи в |
|
квадратурах – в виде интегралов (7.9) и (7.12). Вычислив инте-
грал в (7.9), мы сможем получить |
как функцию времени . |
|
Уравнение (7.12) позволяет найти |
уравнение траектории |
|
, подставляя в которое найденную функцию |
, |
|
можно получить зависимость |
. Роль четырех посто- |
|
янных интегрирования, получающихся при решении уравнений движения, в уравнениях (7.9) и (7.12) играют величины
.
Различные важные особенности общего решения легко получить путем приведения рассматриваемой задачи о движении частицы в центральном поле к эквивалентной одномерной задаче. Уравнение движения (7.7) можно трактовать как уравнение воображаемого одномерного движения, если считать, что на частицу массы m действует «эффективная» сила
Такой одномерной задаче будет соответствовать «эффективная» потенциальная энергия, имеющая вид
82

Если переписать второе слагаемое в правой части выражения (7.13) в виде
можно заключить, что оно представляет собой центробежную силу инерции. Поэтому величину , входящую в выражение (7.15), называют центробежной энергией.
Аналогично рассмотренной выше задаче истинного одномерного движения, область допустимых значений определяется неравенством Условие
определяет границы области движения по расстоянию от центра. При выполнении равенства (7.16) радиальная скорость обращается в нуль, однако, в отличие от истинного одномерного движения, это не означает остановки частицы, поскольку имеется отличная от нуля угловая скорость . Условие (7.16) определяет «точки поворота» траектории, в которых функция переходит от увеличения к уменьшению и наоборот. Траектория при этом будет симметрична относительно точек по-
ворота.
Если область возможных значений ограничена только одним условием движение является инфинитным: траектория частицы приходит из беско-
rmax
нечности и уходит в бесконечность.
Если же область изменения |
имеет |
|
|||
две границы, т.е. |
|
|
|
rmin |
|
то движение является финитным, и |
|||||
|
|||||
траектория будет |
лежать |
внутри |
|
||
кольца, ограниченного окружностя- |
|
||||
ми с радиусами |
и |
(рис. 7.2). |
Рис. 7.2 |
||
|
|
|
|
||
83

Определим условие, при котором траектория финитного движения будет замкнутой. Согласно уравнению (7.12), при изменении от до и затем снова до , угол изменится на величину
Траектория будет замкнутой, если |
является рацио- |
нальной частью от , т.е. |
|
где , – целые числа. В этом случае за таких периодов ра- диус-вектор, совершив полных оборотов, совпадет сам с собой.
В общем случае, при произвольном виде функции , траектория не будет замкнутой и будет бесконечное число раз проходить через точки поворота и . Согласно теореме Бертрана, условие замкнутости траектории (7.18) выполняется только для двух типов притягивающих центральных полей – в которых функция U пропорциональна или . Первый тип (рассматриваемый далее) соответствует силе, обратно пропорциональной квадрату расстояния (например, сила гравитационного взаимодействия или сила Кулона), а второй – силе, пропорциональной радиальному расстоянию, т.е. подчиняющейся закону Гука.
7.2. Задача Кеплера
Рассмотрим теперь конкретный вид центрального поля:
84

где |
– постоянная, |
соответствует притягивающему по- |
лю, |
– отталкивающему. Примерами такого поля являют- |
|
ся поле тяготения (притягивающее) и электростатическое кулоновское поле (может носить как характер притяжения, так и отталкивания). На движущуюся в таком поле материальную точку будет действовать сила, величина которой обратно пропорциональна квадрату расстояния:
Найдем форму траектории, подставив функцию (7.19) в общее решение (7.12) (интеграл оставим неопределенным):
Здесь |
|
– константа, определяемая из начальных условий. |
|||||||||||||||||||||||||||
Выполним |
интегрирование, сделав подстановку |
: |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
85

где – постоянная. Отсюда получаем
следовательно,
или
Мы представили решение в виде, совпадающем с известным из аналитической геометрии уравнением конического сечения в полярных координатах с началом координат в фокусе. Величина p, имеющая размерность длины, называется параметром конического сечения, а безразмерная величина e –
эксцентриситетом. Таким образом, мы получили первый за-
кон Кеплера: траектория движения в центральном поле вида (7.19) есть коническое сечение, один из фокусов которого совпадает с центром поля, а параметр и эксцентриситет равны
Напомним, что коническое сечение есть геометрическое место точек, для которых отношение расстояний до точки фо-
86
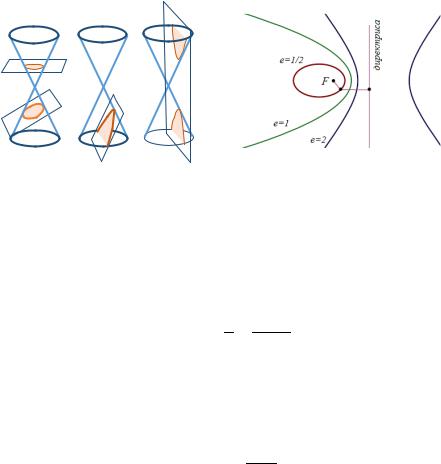
куса и некоторой прямой (директрисы) равно постоянной величине – эксцентриситету e. Данную плоскую кривую можно получить пересечением плоскости с круговым конусом (рис.
7.3). При |
коническое сечение представляет собой эл- |
|
липс, при |
– параболу и при |
– гиперболу (рис. 7.4). |
Рис. 7.3 |
Рис. 7.4 |
Определим условия, при которых реализуется каждый конкретный тип конического сечения. Рассмотрим сначала притягивающее поле, когда . Запишем согласно соотношению (7.14) эффективное поле
при |
и |
при |
. Из условия |
|
находим, что функция |
имеет мини- |
|
мум при |
, равный |
|
|
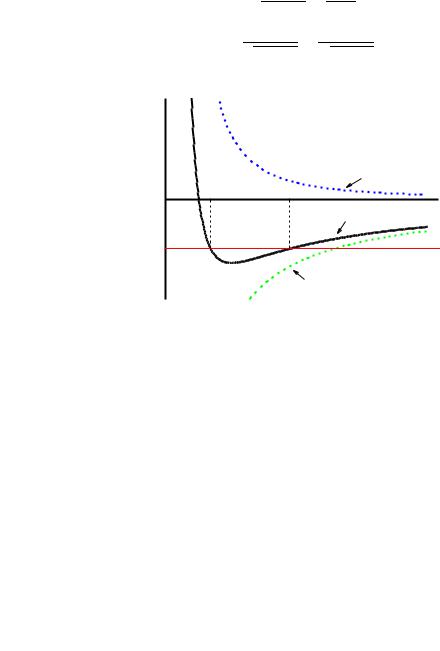
Как видно из графика |
(рис. 7.5), при |
|
|
дви- |
|
||||
жение будет финитным, а при |
– инфинитным. |
|
||
87
Согласно соотношению (7.26), для эксцентриситет
. В этом случае уравнение (7.25) описывает эллипс с большой и малой полуосями, равными соответственно
U |
|
|
|
l2/(2mr2) |
|
rmin |
rmax |
|
0 |
|
r |
|
Uэфф(r) |
|
|
|
|
E |
|
|
|
U(r)=- /r |
|
|
Рис 7.5 |
|
|
Рис. 7.5 |
|
Отметим, что длина большой полуоси a зависит только от энергии E. Если энергия принимает минимально возможное
(для данного момента импульса) значение |
|
, то |
и эл- |
|
липс вырождается в окружность.
При выводе уравнения орбиты (7.25) мы выбрали знак плюс в общей формуле (7.12). Очевидно, изменение знака на противоположный равносильно добавлению к постоянной
. Выбор положительного знака соответствует тому, что при величина r будет минимальна, а при –
максимальна. Эти значения r равны соответственно
88
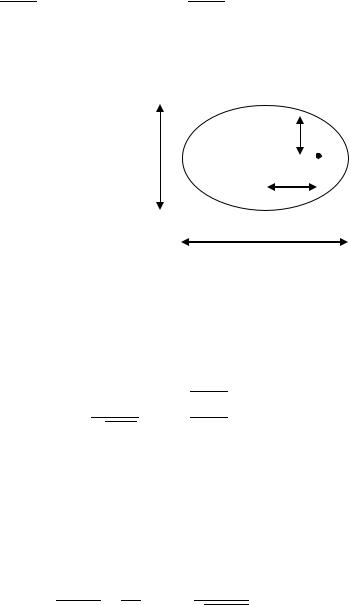
В астрономии соответствующие точки орбиты называют пери-
гелием и афелием. Обычно полагают |
, в этом случае |
|||||||||||||||
значение угловой координа- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ты |
соответствует пе- |
|
|
|
|
|
|
|
|
|
|
y |
||||
ригелию, а |
– афелию |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(рис. 7.6). |
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найдем |
период |
обра- |
|
|
|
|
|
|
|
|
|
|
|
|||
2b |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
O |
x |
||||||||
щения |
по |
эллиптической |
|
|
|
|
|
|
|
ae |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
орбите, что проще всего |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
сделать при помощи соот- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ношения для второго закона |
|
|
|
|
|
2a |
|
|
|
|
||||||
Кеплера (7.5). Проинтегри- |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ровав это соотношение от 0 |
|
|
|
|
|
Рис. 7.6 |
|
|
|
|
||||||
до T, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя |
площадь |
|
|
|
эллиптической |
орбиты |
||||||||||
и учитывая соотношения (7.29), получим
Квадрат периода будет пропорционален кубу большой полуоси – данное утверждение представляет собой третий закон Кеплера.
Если энергия , то и траекторией движения будет огибающая центр поля ветвь гиперболы (рис. 7.7), действительная и мнимая полуоси которой равны соответственно
89

Расстояние перигелия будет равно
Поскольку величина r не может быть отрицательной, то допустимые значения угла должны удовлетворять условию
или
На граничных значениях угла траектория уходит в бесконечность, что соответствует инфинитному характеру движения.
В случае |
получим |
, т.е. частица будет дви- |
|
гаться по параболе с расстоянием перигелия |
. Фи- |
||
зически данный случай соответствует нулевой скорости частицы на бесконечности.
|
y |
y |
|
p |
x |
|
|
O |
|
||
O |
x |
||
|
Рис. 7.7 |
Рис. 7.8 |
Рассмотрим теперь случай отталкивающего поля |
|
, когда |
В этом случае эффективное поле (7.27) при |
изменении от 0 до |
монотонно убывает от до 0. Следова- |
90
