Методическое пособие 401

3. Используя стандартный генератор равномерно распределенных случайных чисел, сформировать генератор белого гауссовского шума. Параметры генератора выбираются из табл. 3 в зависимости от номера варианта. Вывести график полученной реализации случайного сигнала, его СПМ, математическое ожидание и дисперсию, а также гистограмму.

Изменение математического ожидания и дисперсии следует производить по следующей формуле:

ri Ri ,

где ri – i-й отсчет выходного сигнала; – требуемое математическое ожидание; Ri – i-й отсчет исходного

19

случайного сигнала с нулевым математическим ожиданием и единичной дисперсией; 2 – требуемая дисперсия.

4.Получить случайный процесс, используя метод формирующего фильтра. Тип формирующего фильтра и его коэффициенты выбираются из табл. 3 в зависимости от номера варианта. Для всех вариантов порядок используемых фильтров

–2.

5.Вывести график полученного случайного сигнала, математическое ожидание и дисперсию, реальную и теоретическую СПМ, а также гистограмму полученной реализации.

Контрольные вопросы

1.Чем объясняется широкое применение моделей случайных сигналов как моделей информационных процессов при проектировании и отладке информационно-измерительных систем?

2.По какому принципу работают генераторы псевдослучайных последовательностей с равномерным распределением?

3.Какими способами можно преобразовать случайную величину с равномерным распределением в «гауссовскую»?

4.Чем отличаются спектры белого равномерного и белого гауссовского случайного процесса?

5.Перечислите методы моделирования гауссовских случайных процессов.

6.Чем отличаются спектры случайных процессов, построенных с помощью АР-фильтров от спектров случайных процессов, построенных с помощью СС-фильтров?

20

Лабораторная работа № 3 Моделирование инерциальной навигационной системы

Цель работы: научиться моделировать свойства и характеристики навигационной системы

Теоретические сведения

Моделирование проводится на примере бесплатформенной инерциальной навигационной системы (ИНС). В отличие от платформенной ИНС. блок чувствительных элементов (ЧЭ) бесплатформенной ИНС расположен жестко на борту объекта. Следовательно, оси чувствительности элементов изменяют свое положение в пространстве вместе с объектом. В этих условиях возникает задача: как определить угловые параметры, характеризующие положение объекта относительно выбранной системы координат, как определить вектор скорости в этой системе координат, а затем сами координаты объекта. Рассмотрим решение наиболее массовой задачи, когда определяют параметры движения относительно географического сопровождающего трехгранника. Решение зависит от вида используемых измерителей параметров углового движения.

Такие измерители позволяют измерять:

угловые скорости объекта в связанной с объектом системе координат (лазерные гироскопы, волоконнооптические гироскопы, динамически настраиваемые гироскопы, твердотельные волновые гироскопы, обычные и микромеханнческне гнротахометры - все они могут быть названы датчиками угловой скорости (ДУС));

углы поворота объекта (одноосные гиростабилизаторы. интегрированный выходной сигнал ДУС):

направляющие косинусы (гироскопы со сферическим ротором – электростатические, магнитные, с газовым подвесом).

21

Системы координат. Кинематические уравнения и преобразование координат

Алгоритм инерциальной навигационной системы [6] представляет собой замкнутую систему аналитических зависимостей, позволяющую по входным данным (показаниям гироскопов и акселерометров, введенным начальным данным) определять необходимые выходные величины. Схему, изображающую функциональные связи между отдельными аналитическими зависимостями, называют иногда моделирующей схемой алгоритма.

Опишем системы координат и связи между ними, а также модели фигуры Земли и гравитационного ускорения [7].

В качестве модели фигуры Земли будем использовать эллипсоид с параметрами Ф.Н. Красовского:

- большая полуось а= 6 378 245 м; - малая полуось b = 6 356 856 м;

- сжатие a b 0,003352 ; a

При моделировании будем использовать правую декартову систему координат.

1. Инерциальная геоцентрическая экваториальная система координат i(i1, i2, i3) (рис. 11). Начало системы координат (СК) находится в центре Земли. Орт i2 направлен вдоль оси вращения Земли, орты i1, i3 лежат в плоскости экватора, причем в начальный момент времени t0 орт i3 лежит в плоскости Гринвичского меридиана.

СК i сохраняет неизменное угловое положение по отношению к направлениям на удаленные звезды.

22

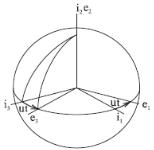
Рис. 11. Инерциальный и земной геоцентрические базисы

2. Земная геоцентрическая экваториальная система координат е (e1, e2, e3) (рис. 11). Начало СК находится в центре Земли. Орт e2 направлен вдоль оси вращения Земли, орты e1, e3 лежат в плоскости экватора, причем орт e3 в любой момент времени находится в плоскости Гринвичского меридиана. Орты e1, e3 вращаются вместе с Землей с угловой скоростью u = 7,29·10–51/с вокруг орта e2. В начальный момент времени t0 орты системы e совпадают с одноименными ортами системы i. Ориентация СК е относительно i в произвольный момент времени t описывается матрицей направляющих косинусов Cei.

В обозначении матрицы направляющих косинусов Cei (табл. 4) верхние индексы показывает название исходного базиса (правый индекс) и конечного базиса (левый индекс). В нашем примере Cei обозначает преобразование от базиса i к

верхние индексы используют аналогично, а нижний индекс показывает, на какую систему координат проектируется угловая скорость.

23

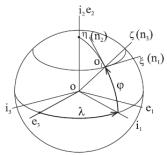
Таблица 4

Матрица направляющих косинусов

3. Географический сопровождающий трехгранник g (O1, n1, n2, n3) (рис. 12). Начало трехгранника O1 находится в центре масс объекта. Орт n3 направлен вдоль вертикали в точке нахождения объекта, орты n1, n2 лежат в плоскости местного горизонта, причем орт n2 лежит также в плоскости меридиана и направлен на Север, а орт n1 направлен на Восток. Часто используют обозначения осей или E N H.

Рис. 12. Географический сопровождающий трехгранник

Угловое положение базиса g относительно базиса е определяется углами долготы и географической широты φ точки местоположения объекта.

Взаимная ориентация систем координат описывается матрицей Cge (табл. 5).

24

Таблица 5

Матрица направляющих косинусов

4. Приборная система координат b (p1, p2, p3). Начало СК находится в месте установки основания приборного блока. Орты p1, p2, p3 направлены параллельно строительным осям объекта, орт p1 – вдоль поперечной, орт p2 – вдоль продольной, орт p3 – вдоль вертикальной осей. Эти оси обозначают также буквами xyz или xcyczc.

Угловое положение приборной СК относительно географического трехгранника b описывается тремя углами: угол курса k, угол тангажа , угол крена (рис. 13).

Рис. 13. Углы поворота объекта с курсом

Взаимная ориентация СК b относительно g описывается таблицей направляющих косинусов Cbg табл. 6.

25

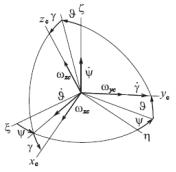
Если положение объекта в азимутальной (горизонтальной) плоскости задают не углом курса k, а углом рыскания , как показано на рис. 14, матрица Cbg имеет вид

(табл. 7).

Рис. 14. Углы поворота объекта с рысканьем

Приведенное преобразование можно выразить с помощью параметров Родрига-Гамильтона, которые являются

26

компонентами четырехмерного комплексного числа – кватерниона. Кватернион поворота системы координат из одного положения в другое имеет вид:

системы координат.

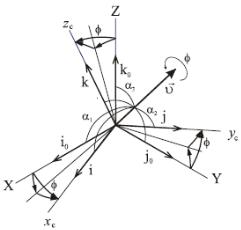
Кватернион описывает поворот тела (связанной с ним системы координат) относительно мгновенной оси на угол

(рис. 15).

Рис. 15. Поворот системы координат

где l, т. п – направляющие косинусы углов ai (i = 1,2,3 соответственно), определяющих положение оси поворота. Иногда кватернион записывают в виде:

или в виде

27

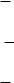
i 1 j 2 k 3 4

Впрограмме лабораторной работы используется последняя форма. Для нее матрица направляющих косинусов может быть представлена через параметры РодригаГамильтона следующим образом:

Для параметров кватерниона справедливо соотношение:

Отсюда, диагональные элементы можно представить в

Текущие значения параметров находят из кинематических уравнений. Если рассматривают движение в инерциальной системе координат, уравнения имеют вид:

Ввекторно-матричном виде уравнения можно

представить следующим образом:

28