Методическое пособие 389

Полагая x1 m , где m – любое неравное нулю число, получим x2 = 3m .

Значит собственный вектор, соответствующий собственному числу λ1 = 9 , имеет вид хλ=9 = {m,3m}.

Аналогично для λ2 = –1 получим хλ=-1 = {−3m, m }. Если положить, например, m = 1 , то получим

х1 = {1,3}, x2 = {−3,1).

Пример 2. Найти собственные векторы оператора, заданного матрицей

Так как 0<α< π, и cos 2α<1 , то дискриминант отрицательный и корней

уравнение не имеет, поэтому характеристическое уравнение не имеет действительных корней. Следовательно, данный оператор не имеет собственных векторов.

Собственные векторы играют важную роль в теории линейных преобразований, а именно, если в качестве базиса взять собственные векторы, то в таком базисе оператор имеет особенно простое представление и вполне определяется собственными числами. Покажем это.

Пусть задан линейный оператор y Ax в пространстве R3. Предполо-

жим, что имеются три некомпланарных собственных вектора этого оператора e1 ,e2 ,e3 c собственными числами λ1 ,λ2, λ3. Так как векторы e1 ,e2 ,e3 некомпла-

нарные, то их можно взять в качестве базиса. Выразим теперь в проекциях представление данного преобразования в этом базисе. Для этого обозначим через e1,e2 ,e3 образы векторов e1,e2 ,e3 соответственно.

Тогда e1 Ae1 1e1 , e2 Ae2 e2 , e3 Ae3 e3 .

Отсюда имеем

61

Так как A* A , то

Итак, если в качестве базиса взяты собственные векторы данного линейного оператора, то матрица этого оператора имеет диагональный вид (4.22) , где на главной диагонали стоят собственные числа векторов e1 ,e2 ,e3 в поряд-

ке их нумерации. Имея матрицу линейного оператора, можно это преобразование записать в проекциях

y1 1 x1 , y2 2 x2 ,

y3 3 x3 .

Всерассужденияможноаналогичнопровестидля n гопространства Rn .

Замечание. Однако не для всякого линейного оператора возможно такое упрощение матрицы. Мы видели на предыдущем примере, что встречаются такие операторы, которые вовсе не имеют собственных векторов. Для таких операторов выбрать базис из собственных векторов нельзя.

3.1. Симметрические линейные преобразования

Пусть линейный оператор задан матрицей А.

Матрица называется симметрической, если она совпадает со своей транспонированной A* A , другими словами, если ai, j a j,i .

У симметрической матрицы элементы, расположенные симметрично относительно главной диагонали, равны между собой.

Приведем две важные теоремы (доказательства приведены в прил.). Теорема 1. Характеристическое уравнение симметрической матрицы

имеют только действительные корни.

Теорема 2. Собственные векторы симметрического линейного преобразования ортогональны друг другу.

Втеории также доказывается, что для каждой симметрической матрицы

Àможно подобрать такую ортогональную матрицу B , для которой матрица

B 1 AB будет диагональной, причём на диагонали будут стоять характеристические числа матрицы À .

Рассмотрим евклидово пространство E2 , в котором введено скалярное произведение (X ,Y ) .

62

Линейный оператор À * называется сопряжённым к оператору À , если для любых векторов X и Y выполняется равенство

(AX ,Y ) (X , A *Y ) .

Для всякого оператора À сопряжённый оператор À * существует и единственный.

Если оператор À имеет матрицу À = (ai, j ) , то сопряжённый оператор

À * в том же базисе имеет матрицу À *= (a *i, j ) , где ai, j * ai, j .

В частном случае, если пространство евклидово, то À *= À Т.

Это видно, например, из линейного преобразования поворота системы координат.

Линейный оператор À в евклидовом пространстве называется самосопряжённым, если À = À *.

§ 4. Квадратичные формы

Рассмотрим n мерное пространство векторов x1, x2 , x1 . Возьмем всевозможные парные произведения переменных x1, x2 (i 1,2,...n , j 1,2,...n.)

и составим сумму этих произведений:

где aij – некоторыекоэффициенты, средикоторых, хотябыодинотличенотнуля.

Эта сумма называется квадратичной формой n переменных и будем ее обозначать F(x1, x2 ,...xn ).

Для удобства квадратичную форму записывают в таком виде, что коэф-

Например, 2x1x2 4x2 x1 6x1x2 3x1x2 3x2 x1 .

Поэтому будем всегда считать, что в квадратичной форме aij a ji , а все рассуждения проводить в трехмерном пространстве R3( x1, x2 , x3 ).

63

Квадратичная форма в R3 будет иметь вид

F(x1, x2 , x3 ) a11x12 a22 x22 a33 x32 2a12 x1x2 2a13 x1x3 a23 x2 x3. (4.24)

Составим матрицу из коэффициентов квадратичной формы:

Эта матрица является симметрической, так как ее коэффициенты, симметричные относительно главной диагонали, равны между собой, и называ-

ется матрицей квадратичной формы F .

Представим квадратичную форму в матричном виде. Для этого сделаем следующие преобразования:

F x1 (a11x1 a12x2 a13x3 ) x2 (a12x1 a22x2 a13x3 ) x3 (a13x1 a23x2 a33x3 ) XY,

где X (x1, x2 , x3 ),

64

Пример 2. Найти квадратичную матрицу, соответствующую матрице

Решение. F x2 5x22 2x32 4x1x2 6x1x3 2x2 x3.

Если квадратичная форма содержит только члены с квадратами переменных

т.е. является диагональной. В этом случае квадратичная форма называется

канонической.

Обратно, каждая каноническая форма имеет диагональную матрицу. Таким образом, чтобы квадратичную форму привести к каноническому виду, нужно выбрать такой базис, в котором соответствующая матрица была бы диагональной.

Как уже отмечалось, любую симметрическую матрицу можно привести к диагональному виду, если в качестве нового базиса взять ее собственные векторы, причем новый базис является ортогональным, который к тому же можно нормировать. Для этого достаточно проекции собственных векторов разделить на их нормы (модули). Другими словами, мы должны осуществить такое преобразование координат, в результате которого квадратичная форма в новом ортонормированном базисе принимает канонический вид. Пусть

65

Пример 1. Привести к каноническому виду квадратичную форму

F 4x12 4x22 x32 12x1x2 .

Решение. Составим матрицу этой квадратичной формы

Получаем λ1= 1, λ2=-2, λ3=10.

Следовательно, F y12 222 10y32 .

Для двух переменных квадратичная форма имеет наиболее простой вид:

F(x1, x2 ) a11x12 a22 x22 a33 x32 .

Решив это уравнение, находим собственные числа 1 , 2 . Тогда квадратичная форма принимает канонический вид

F(x1x2 ) 1 y12 2 y2 2 .

§ 5. Линейная модель обмена

В качестве примера математической модели экономического процесса, приводящейся к понятию собственного вектора и собственного значения матриц, рассмотрим линейную модель обмена (модель международной торговли).

Пусть имеется n стран S1, S2 ,...Sn , национальный доход каждой из которых равен соответственно x1, x2 , x3 ,...xn .Обозначим коэффициентами aij долю национального дохода, которую страна Sij тратит на покупку товаров у

страны Si . Будем считать, что весь национальный доход тратится на покупку товаров либо внутри страны, либо на импорт из других стран, т.е.

n

aij 1 ( j 1,2,..n) . (4.31)

i 1

66

которая называется структурной матрицей торговли.

Согласно (4.31) сумма элементов любого столбца этой матрицы равна 1. Для любой страны S j ( j 1,2,...n) выручка от внутренней и внешней

торговли составит pi ai1x1 ai2 x2 ... ain xn .

Для сбалансированной торговли необходима бездефицитность торговли каждой страны Si , т.е. выручка от торговли каждой страны должна быть не

меньше ее национального дохода, т.е. pi xi . Введя вектор

x x1 , x2 ,..., xn национальныхдоходовстран, получимматричноеуравнение

AX X ,

где X матрица-столбец из координат вектора x . Таким образом, задача свелась к отысканию собственного вектора матрицы A , соответствующего собственному числу 1.

Пример. Структурная матрица торговли трех стран S1,S2 , S3 имеет вид

Полученный результат означает, что сбалансированная торговля трех стран достигаетсяприсоотношениинациональныхдоходовстран 32 :2:1 или3:4:2.

67

9. Привести к диагональном виду матрицы линейных операторов:

x1 2 y1 y2 , x2 y1 y2 .

13. Найти соотношение цен трех товаров, если наборы этих товаров x1 (6;2;4), x2 (1;8;9), x3 (3;5;9)

Глава 5. УРАВНЕНИЕ ЛИНИИ

§ 1. Простейшие задачи аналитической геометрии на плоскости

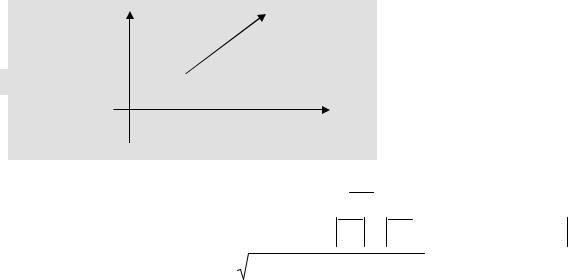
1.1. Расстояние между двумя точками.

A( x1 y1)

Рис. 5.1

На отрезке AB (рис. 5.1) строим вектор AB , тогда расстояние между точками равно модулю этого вектора: AB AB{(x2 x1 ),( y2 y1 )} ,

69

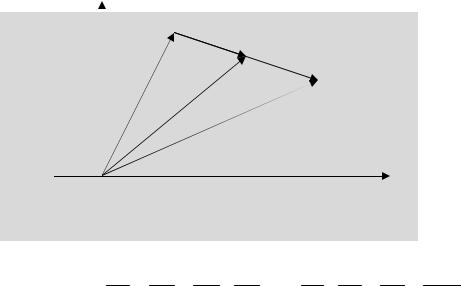
1.2. Деление отрезка в данном отношении

Говорят, что точка С делит отрезок в отношении , если CBAC . Задача

состоит в том, чтобы, зная координаты точек А и В и отношение , в котором точка С делит отрезок АВ, определить координаты точки С.

y

A(x1, y1 ) С(x, y)

B(x2 , y2 )

Рис. 5.2

Из рис. 5.2 следует:

OA AC OC , AC CB , CB OB OC ,

В частном случае, если точка С делит отрезок пополам, то есть находится на середине отрезка, то 1 и формула (5.2) принимают вид:

§ 2. Уравнение линии на плоскости

Каждой точке на плоскости соответствует пара действительных чисел ( x, y ) (координаты). Возникает вопрос, что соответствует некоторой кривой

линии на плоскости?

Например, что соответствует известной линии окружности на плоскости? Окружность есть геометрическое место точек плоскости, равноудаленных от точки С( a,b), называемой центром, на одинаковом расстоянии R , на-

зываемом радиусом.

70