Лекція 4

Лекція 4

Множинна лінійна регресія

1. Теоретичне та емпіричне лінійні рівняння

2. Відхилення в матричній формі

3. Оператор оцінювання класичного МНК

4. Дисперсійно-коваріаційна матриця параметрів регресії

5. Множинна кореляція та детермінація

6. Тест Фішера (на адекватність моделі)

7. Перевірка гіпотез щодо параметрів багатофакторної регресії

8. Довірчі інтервали

Множинна лінійна регресія

Як правило, декілька причин є впливовими на будь-який чинник (економічний показник).

Замість парної регресії розглядається множинна

Найбільш вживана і досить проста модель множинної лінійної регресії.

Теоретичне лінійне рівняння регресії

Для індивідуальних спостережень числом n (i = 1, 2, …, n)

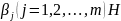j-m теоретичн. коеф. регресії: характеризує чутливість Y до зміни X; або відображає вплив на умови математичного сподівання залежн. зм. Y пояснювальної зм. Хj при сталості всіх інших.

оцінювання , для яких має місце найкраще наближення при спостереженнях; часткові коефіцієнти регресії

число ступенів вільності. Вважається: при оцінюванні множинною лінійною регресією для забезпечення статистичної надійності вимагається, що число спостережень щонайменше в 3 р. перевищувало число оцінюваних параметрів.

Емпіричне рівняння регресії записується

,

оцінки для ; .

Для індивідуальних значень

За даними вибірки об’єму n треба оцінити значення параметрів (параметризація моделі).

Відхилення

Скористаємося матричними позначеннями:

n – вимірний стовпець (вектор) спостережень;

Матриця n * (m+1) вимірності спостережень, i-й рядок якої відповідає спостереженням вектора значень незалеж. зм. ;

Зауваження!

вектор-стовпець коефіцієнтів рівняння регресії

вектор-стовпець відхилень реальних значень yi залежної зм. Y від модельних, отриманих по рівнянню регресії.

Економетрична матрична модель записується

В матричній формі похибка записується , її квадрат має вигляд .

Результатом процедури МНК у матричній формі буде вираз

,

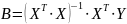який називається оператором оцінювання 1 МНК, ним визначаються емпіричні коефіцієнти множинної лінійної регресії.

Зауваження. Якщо незалежні змінні в матриці Х взяти як відхилення кожного значення від свого середнього, то величина ( ) назив. матрицею моментів. Елементи її головної діагоналі є величини дисперсії незалежних змінних, інші елементи відповідають взаємним коваріаціям.

В матричній формі похибка записується утворимо квадрат похибки

,

де індекс Т – транспонування; матричні співвідношення:

відомі.

Умова існування extr:

Якщо незалежні змінні в матриці Х взяті як відхилення кожного значення від свого середнього, то матрицю назив. матрицю моментів.

Структура матриці моментів відбивав зв’язки між незалеж. змінними.

Зауваження. Вираз назив. оператором оцінювання 1 МНК, тобто ним визначаються емпіричні коеф. множинної лінійної регресії.

Дисперсійно-коваріаційна матриця параметрів регресії (оцінок параметрів моделі) записується

На головній діагоналі матриці містяться оцінки дисперсії параметрів, інші її елементи відображають оцінки коваріації між bj та bk параметрами.

Має місце

,

де дисперсія ВВ її формули

Нехай Cjk елемент матриці , на перетині j-го рядка і k-го стовпця. Тоді елементи головної діагоналі дисперсійної матриці обчислюються як , інші її елементи як .

Стандартні помилки оцінок параметрів моделі є

У випадку лінійної регресії коефіцієнт детермінації дорівнює квадратної вибіркового коефіцієнта кореляції між двома рядами спостережень – експериментальними значеннями регресанда (yi) і його розрахункового .

.

Враховано, що класич. регрес. моделі .

Мірою ступеня відповідності модельних даних фактичним 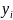(і- 1, 1,… n) є коефіцієнт множинної кореляції

R= Для класичної регресійної моделі

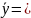
Його квадрат є коефіцієнтом множинної детермінації

<≡

Як у випадку простої лінійної регресії: SST=SSE+SSR<=>

=1= ≡

При зростанні кількості факторів також ↑ і ніколи не зменшується.

Розглядається оцінений коефіцієнт детермінації

(скориговані на їхні ступені вільності)

Суми квадратів у чисельнику та знаменнику діляться на відповідні ступені вільності, в яких ураховується число факторів моделі

Має місце формула (k>1; ).

Якщо кількість факторів ↑, то оцінений коефіцієнт детермінації ↑ повільніше, ніж . Цим користуються при порівнянні різних регресійних моделей.

Перевірка моделі на адекватність за F-критерієм Фішера

Нульова гіпотеза Н₀: =0 (j=1…m) <=> H₀:

Проти альтернативної Н₁: хоча б одне =0

Для перевірки Н₀ гіпотези розраховується F-статистика Фішера з m та

(n-m-1) ступенями вільності

, де -число факторів; - число спостережень.

За F-таблицями Фішера шукається критичне значення з та α-рівнем помилки (або (1-α)100% рівнем довіри).

Якщо F > , то нуль-гіпотеза відкидається; модель адекватна. У протилежному випадку нульова гіпотеза приймається, модель неадекватна.

F-тест, який є мірою адекватності регресійної моделі, також виступає мірою статистичної значущості коефіцієнта детермінації.

Зауваження! F-відношення Фішера (статистика) розраховується на підставі формули:

F= , k=m+1

За F-таблицями Фішера шукається (k-1; n-k; α- рівень помилки)

Якщо F > (k-1; n-k; α), тоді Н відкидається; у протилежному випадку приймається. Таким чином, тестування на адекватність моделі за допомогою тільки коефіцієнтів детермінації.

Перевірка гіпотез щодо параметрів багатофакторної регресії у матричному вигляді

Кожний параметр відповідає В~Ɲ [β, нормальний закон розподілу, де β- матем. сподівання=параметру узагальненої регр.моделі

Заміна справжнього значення дисперсії ВВ на його оцінку приводить до того, що Ʉ елемент вектора В відповідає t-розподілу Стьюдента з (n-k) ступенями вільності.

Задаємось α*100% рівнем значимості; для кожного параметра окремо будується t-статистика

t = з (n-k) ступенями вільності, де - оцінка параметра ; - гіпотетичне значення, яке має прийняти ; 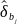- оцінка дисперсії параметра (з регресії); n- кількість спостережень; k- загальна кількість оцінених параметрів.

В економетриці поширеною формулою нуль-гіпотези є така:

Н₀: = 0.

t-статистика є = її значення порівнюються з табличним, яке дає змогу знайти критичну зону з (n-k) ступенями вільності.

Якщо потрапляє не у критичну зону, то з ймовірністю (1-α) 100% оцінка є статистично незначима (Н₀ приймається)

В протилежному випадку – Н₀ відкидається.

Зауваження! =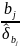 є відношення до оцінки свого стандартного відхилення (середнього квадратичного).

Після перевірки адекватності моделі та значимості знайдених параметрів за t-критерієм Стьюдента виконуються прогнози, будуються інтервали довіри, вивчається вплив окремих факторів на залежний чинник.

По аналогії з процедурою тестування нуль-гіпотези для параметрів за t-тестом Стьюдента інтервали довіри записуються

= ± .

Побудова довірчих інтервалів: для математичного сподівання залежної змінної з рівнем довіри (1-α) 100% здійснюється за формулою

Або в матричній формі

<= M (Y│X₀) <= ,

Де = Х₀В розглядається як точкова оцінка математичного сподівання прогнозного значення Y₀, а також як індивідуальне значення Y₀ для вектора незалежної мінної Х₀, що лежить за межами базового періоду.

Для індивідуального значення залежної змінної

<= Y₀<= ;

В координатній формі

.