
Лекція 6 (2)
.docxЧислові розв’язування задачі лінійного програмування(ЛП)
План:
Симплекс-алгоритм розв’язування задачі ЛП:
А)Початкова симплекс-таблиця;
Б)Правила утворення наступної симплекс-таблиці.
2.Умови застосування класичного симплекс-метода.
3.Дослідження задачі ЛП.
4.Метод штучного базису.
5.Елементи теорії задачі ЛП.
Симплекс-таблиця задачі ЛП
Стандартна форма задачі:
-2x1+x2≤2; x1-2x2≤2; x1+x2≤5; x1≥0; x2≥0.

для обмежень:
 Канонічна
форма задачі:
Канонічна
форма задачі:
Z= -x1+x2+0*x3+0*x4+0*x5min
додаткові змінні
-2x1+x2+x3=2;
x1-2x2+0*x3+x4=2;
x1+x2+0*x3+0*x4+x5=5;
xj ≥0, де j=1, 2, ... ,5.
Інша форма запису канонічної задачі ЛП:
 =
=
 ,
де
,
де


Табличне відображення:
СБj |
|
|
-1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|||
0 |
x3 |
2 |
-2 |
1 |
1 |
0 |
0 |
0 |
x4 |
2 |
1 |
-2 |
0 |
1 |
0 |
0 |
x5 |
5 |
1 |
1 |
0 |
0 |
1 |
Індексна строка ↔∆j |
0 ∆0 |
1 ∆1 |
-1 ∆2 |
0 ∆3 |
0 ∆4 |
0 ∆5 |
|
Перший базисний розв’язок:
 =
(x1;
x2;
x3;
x4;
x5)
≡
(0;
0; 2; 2; 5),
=
(x1;
x2;
x3;
x4;
x5)
≡
(0;
0; 2; 2; 5),
мовою економіки - нічого не виробляється.
Таблиця
СBj |
|
|
-1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|||
0 |
x3 |
2 |
-2 |
1 |
1 |
0 |
0 |
0 |
x4 |
2 |
1 |
-2 |
0 |
1 |
0 |
0 |
x5 |
5 |
1 |
1 |
0 |
0 |
1 |
Індексна строка ∆j |
0 ∆0 |
1 ∆1 |
-1 ∆2 |
0 ∆3 |
0 ∆4 |
∆5 |
|
Першу колонку СBj складають коефіцієнти цільової функції біля базисних змінних.
Друга колонка є базисні змінні.
Третя колонка відповідає координатам (обмеженням ресурсів).
Наступні
5 колонок відповідають
коефіцієнтам біля невідомих системи
обмежень, причому над
стовпцями
 стоять коефіцієнти функції мети.
стоять коефіцієнти функції мети.
Як заповнюється індексна строка?
Величина
 =
= *
* є
значення лінійної форми для початкового
опорного плану;
є
значення лінійної форми для початкового
опорного плану;
відповідно
 =
*
=
* ,-
,- є числові оцінки вільних змінних.
є числові оцінки вільних змінних.
Застосовується симплекс-алгоритм.
Розв’язок або опорний план буде оптимальний тоді, коли :
Для задачі ЛП на min усі оцінки недодатні, тобто від’ємні або

Для задачі ЛП на max усі величини невід’ємні , тобто додатні або 0
Умови застосування класичного симплекс-метода
Задача ЛП записується в канонічній формі
Для матриці системи обмежень (m рядків, n стовпців) {\displaystyle \operatorname {rang} A}rangA=m, тобто всі рядки лінійно незалежні
Координати вектора запасів додатні
Відомий початковий базисний розв’язок
Усі допустимі базисні розв’язки (опорні плани) є всевироджені (базисні змінні≠0)
Дослідження задачі ЛП2
Симплекс-методом одночасно досліджується розв’язувана задача:
Опорний план (розв’язок) єдиний; коли серед величин – симплекс-різниць оптимального плану нульовими є лише базисні;
Немає розв’язку, коли система обмежень несумісна, що з’ясовується в процесі пошуку початкового базисного розв’язку (опорного плану);
Якщо в симплекс-таблиці задачі ЛП на max для деякої величини
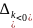 усі елементи k-го
стовпця недодатні, тобто розв’язку
немає, бо цільова функція необмежена
зверху (у випадку задачі ЛП на min
має місце
усі елементи k-го
стовпця недодатні, тобто розв’язку
немає, бо цільова функція необмежена
зверху (у випадку задачі ЛП на min
має місце
 і елементи k-го
стовпця від’ємні, цільова функція
необмежена знизу)
і елементи k-го
стовпця від’ємні, цільова функція
необмежена знизу)Коли серед величин індексної строки нульовими є не тільки базисні, а також інша
 .
.
Альтернативний оптимум
Для
задачі ЛП:

має місце симплекс-таблиця:
СБj |
Базис змінних |
|
1 |
1 |
0 |
0 |
x1 |
x2 |
x3 |
x4 |
|||
0 0 |
x3 |
2 12 0 |
1 4 -1 |
1 3 -1 |
1 0 0 |
0 1 0 |
x4 |
||||||
σj |
||||||
1 0 |
x1 |
2 4 2 |
1 0 0 |
1 -1 0 |
1 -4 1 |
0 1 0 |
x4 |
||||||
σj |
||||||
1 0 |
x2 |
2 6 2 |
1 1 0 |
1 0 0 |
1 -3 1 |
0 1 0 |
x4 |
||||||
σj |
На 2-ій ітерації досягли оптимального розв’язку

Але
серед величин
 нульовими є не тільки базисні
нульовими є не тільки базисні
 також небазисної
також небазисної
 .
.
Утворюється
ще одна симплекс – таблиця (третя,
остання), вводячи в базис
 замість
замість
 :
:

Довільна
оцінка лінійна комбінація оптимальних
розв'язків
 також буде розв'язком
також буде розв'язком
 задачі, що записується:
задачі, що записується:
 ,
де
,
де

ЗАУВАЖЕННЯ! Інший вигляд формули обчислення коефіцієнтів індексної строки:

Метод штучного базису (М-задача)
Застосовується там, де початковий базис безпосередньо не встановлюється (в обмеженнях не виділяється одинична матриця)
Приклад
1:



Жодного одиничного вектора.
Вводяться
штучні
змінні
 :
стільки їх, скільки рівнянь в обмеженнях
задачі ЛП. Цим самим утворюється базис.
Оскільки задача
ЛП на мінімізація лінійної форми,
то
в
ній штучні
змінні
присутні з коефіцієнтами
M>0,
М досить велике число
(для
задачі на max
число М<0).
Таким
чином, будується розширена
задача( М-задача):
:
стільки їх, скільки рівнянь в обмеженнях
задачі ЛП. Цим самим утворюється базис.
Оскільки задача
ЛП на мінімізація лінійної форми,
то
в
ній штучні
змінні
присутні з коефіцієнтами
M>0,
М досить велике число
(для
задачі на max
число М<0).
Таким
чином, будується розширена
задача( М-задача):

 ;
;

 ;
;
 xj
≥0,
де
j=1,
2, ... ,7.
xj
≥0,
де
j=1,
2, ... ,7.
Вона розв’язується симплексним методом. Якщо в такому розвязку всі штучні змінні=0, то є оптимальний план. Якщо хоча б одна штучна змінна в отриманому розв’язку ≠0,то не існує розвязку( оптимального плану початкової задачі.)
Приклад
2:
max
(5 );
);
 =3
=3
 =3;
Xj≥0,
j=1…4
=3;
Xj≥0,
j=1…4
 Нема
одиничних векторів. Через штучні змінні
Нема
одиничних векторів. Через штучні змінні
 i
i
 утворюється
М-задача:
утворюється
М-задача:

 ;
;

xj ≥0, де j=1, 2, ... ,6.
Базові змінні |
СБj |
|
5 |
3 |
4 |
-1 |
-M |
-M |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|||
x5 |
-M |
3 |
1 |
3 |
2 |
2 |
1 |
0 |
x6 |
-M |
3 |
2 |
2 |
1 |
1 |
0 |
1 |
|
(m+1) |
0 |
-5 |
-3 |
-4 |
1 |
0 |
0 |
|
(m+2) |
-6M |
-3M |
-5M |
-3M |
-3M |
0 |
0 |
В
М- задачі ідексна строка зображується
зображується
 рядками:
в першому (m+1)
записується
вільні члени виразів
рядками:
в першому (m+1)
записується
вільні члени виразів
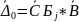 i
i
 ;
;
В другому рядку (m+2) записуються коефіцієнти з величинами M.
ЗАУВАЖЕННЯ! Поки не виключені з базису штучні змінні, критерієм оптимальності служитиме рядок (m+2) індексної строки.
Продовження таблиці
Базові змінні |
СБj |
|
5 |
3 |
4 |
-1 |
-M |
-M |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|||
x2 x6 |
3 -M (m+1) (m+2) |
1 1 3 -M |
1/3 4/3 -4 -4/3M |
1 0 0 0 |
2/3 -1/3 -2 1/3M |
2/3 -1/3 3 1/3M |
1/3 -2/3 1 5/3M |
0 1 0 0 |
x2 x1 |
3 5 (m+1) (m+2) |
3/4 3/4 6 6 |
0 1 0 0 |
1 0 0 0 |
3/4 -1/4 -3 -3 |
3/4 -1/4 2 2 |
1/2 -1/2 -1 -1 |
-1/4 3/4 3 3 |
x3 x1 |
4 5
|
1 1 9 |
0 1 0 |
4/3 1/3 4 |
1 1 0 |
1 0 5 |
2/3 -1/3 1 |
-1/3 2/3 2 |
X2






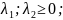
X1
0

Вектори
 утворюють лінійну комбінацію і лежить
в куту, який називається конусом К. При
умові
утворюють лінійну комбінацію і лежить
в куту, який називається конусом К. При
умові
 буде
випукла лінійна комбінація, причому
буде
випукла лінійна комбінація, причому
 ,
,
 і
і
 є (0,1): множині всіх випуклих комбінацій
векторів
і
відповідає прямолінійний відрізок
кінців цих векторів.
є (0,1): множині всіх випуклих комбінацій
векторів
і
відповідає прямолінійний відрізок
кінців цих векторів.
Якщо такими є вершини багатогранника, то кінцевий згадуваному відрізку відповідає ребро.
Теорема 2.
Extr лінійної форми досягається в кутовий точці конуса К. (ОДЗ)
Теорема
3. Якщо
існує множина лінійно незалежних
векторів
 таких, що виконується
таких, що виконується

Для
 ,
то точка
,
то точка
 є кутова для випуклої множини К розв’язків
системи обмежень задачі ЛП.
є кутова для випуклої множини К розв’язків
системи обмежень задачі ЛП.
Теорема
4. (обернена
до теор.3). Якщо
 кутова точка множини К, то існують
лінійно незалежні вектори
такі, що має місце
кутова точка множини К, то існують
лінійно незалежні вектори
такі, що має місце
 для
для


 або
xj
або
xj




 (xj)
(xj)




