звіт лр3

Лабораторна №3: Мультиколінеарність

Лабораторна №4: Гетероскедастичність

Лабораторна №5: Автокореляція

Горбунова Юля

Рівняння множинної регресії може бути представлене у вигляді:

Y = f(β , X) + ε

де X = X(X 1 , X 2 , ..., X m ) - Вектор незалежних (пояснюючих) змінних; β - вектор параметрів (що підлягають визначенню); ε – випадкова помилка (відхилення); Y - залежна (яка пояснюється) змінна.

теоретичне лінійне рівняння множинної регресії має вигляд:

Y = β 0 + β 1 X 1 + β 2 X 2 + ... + β m X m + ε

β 0- вільний член, що визначає значення Y, у разі, коли всі пояснюють змінні X j рівні 0.

Перш ніж перейти до визначення знаходження оцінок коефіцієнтів регресії, необхідно перевірити низку передумов МНК.

Передумови МНК .

1. Математичне очікування випадкового відхилення ε i дорівнює 0 всім спостережень (M(ε i ) = 0).

2. Гомоскедастичність (постійність дисперсій відхилень). Дисперсія випадкових відхилень ε i стала: D(ε i ) = D(ε j ) = S 2 для будь-яких i і j.

3. відсутність автокореляції.

4. Випадкове відхилення має бути незалежно від пояснюючих змінних: Yeixi = 0.

5. Модель є лінійною щодо параметрів.

6. відсутність мультиколлінеарності. Між пояснювальними змінними відсутня строга (сильна) лінійна залежність.

7. Помилки ε i мають нормальний розподіл. Виконаність цієї передумови важлива для перевірки статистичних гіпотез та побудови довірчих інтервалів.

Емпіричне рівняння множинної регресії представимо у вигляді:

Y = b 0 + b 1 X 1 + b 1 X 1 + ... + b m X m + e

Тут b 0 , b 1 , ..., b m- Оцінки теоретичних значень β 0 , β 1 , β 2 , ..., β m коефіцієнтів регресії (емпіричні коефіцієнти регресії); e – оцінка відхилення ε.

При виконанні передумов МНК щодо помилок ε i оцінки b 0 , b 1 , ..., b m параметрів β 0 , β 1 , β 2 , ..., β m множинної лінійної регресії по МНК є незміщеними, ефективними та заможними ( тобто BLUE-оцінками).

Для оцінки параметрів рівняння множинної регресії застосовують МНК.

1. Оцінка рівняння регресії .

Визначимо вектор оцінок коефіцієнтів регресії. Відповідно до методу найменших квадратів, вектор s виходить з виразу: s = (X T X) -1 X T Y

До матриці зі змінними X j додаємо одиничний стовпець та окремо записуємо матрицяю Y. Транспонуємо матрицю X, та перемножаемо на матрицю Х

У матриці, число 20, що лежить на перетині 1-го рядка та 1-го стовпця, отримано як сума творів елементів 1-го рядка матриці X T та 1-го стовпця матриці X

Помножуємо транспоновану матрицю Х на матрицю У.Знаходимо зворотну матрицю

Вектор оцінок коефіцієнтів регресії дорівнює

рівняння регресії (оцінка рівняння регресії)

Y = 18.1829 + 0.09231X 1 + 0.9995X 2 -0.01504X 3

Інтерпретація коефіцієнтів регресії. Константа оцінює агрегований вплив інших (крім врахованих у моделі х i ) факторів на результат Y і означає, що Y за відсутності x i склала б 18.1829. Коефіцієнт b 1 вказує, що зі збільшенням x 1 на 1 Y збільшується на 0.09231. Коефіцієнт b 2 показує, що зі збільшенням x 2 на 1 Y збільшується на 0.9995. Коефіцієнт b 3 вказує, що зі збільшенням x 3 на 1 Y знижується на 0.01504.

2. Матриця парних коефіцієнтів кореляції R .

Число спостережень n = 20. Число незалежних змінних у моделі дорівнює 3, а число регресорів з урахуванням одиничного вектора дорівнює числу невідомих коефіцієнтів. З урахуванням ознаки Y, розмірність матриці стає рівною 5. Матриця, незалежних змінних Х має розмірність (20 х 5).

Значення парного коефіцієнта кореляції свідчить про низький лінійний зв'язок між х 1 і у.

Значення парного коефіцієнта кореляції свідчить про сильний лінійний зв'язок між x 2 і y.

Значення парного коефіцієнта кореляції свідчить про низький лінійний зв'язок між x 3 та y.

Значення парного коефіцієнта кореляції свідчить про низький лінійний зв'язок між х 2 і х 1 .

Значення парного коефіцієнта кореляції свідчить про низький лінійний зв'язок між х 3 і х 1 .

Значення парного коефіцієнта кореляції свідчить про низький лінійний зв'язок між х 3 і х 2 .

Ознаки x та y ∑x i ∑y i ∑x i *y i

Для y та x 1 958 47.9 2022 101.1 97398 4869.9

Для y та x 2 1582 79.1 2022 101.1 160841 8042.05

Для y та x 3 747 37.35 2022 101.1 74916 3745.8

Для x 1 та x 2 1582 79.1 958 47.9 75682 3784.1

Для x 1 та x 3 747 37.35 958 47.9 38527 1926.35

Для x 2 та x 3 747 37.35 1582 79.1 58401 2920.05

Дисперсії та середньоквадратичні відхилення.

Ознаки x та y

Для y та x 1 368.99 63.89 19.209 7.993

Для y та x 2 44.99 63.89 6.707 7.993

Для y та x 3 574.428 63.89 23.967 7.993

Для x 1 та x 2 44.99 368.99 6.707 19.209

Для x 1 та x 3 574.428 368.99 23.967 19.209

Для x 2 та x 3 574.428 44.99 23.967 6.707

Матриця парних коефіцієнтів кореляції R:

- і х 1 х 2 х 3

і 1 0.1772 0.8401 -0.1581

х 1 0.1772 1 -0.03718 0.2982

х 2 0.8401 -0.03718 1 -0.2136

х 3 -0.1581 0.2982 -0.2136 1

Приватні коефіцієнти кореляції .

Коефіцієнт приватної кореляції відрізняється від простого коефіцієнта лінійної парної кореляції тим, що він вимірює парну кореляцію відповідних ознак (y і x i ) за умови, що вплив на них інших факторів (x j ) усунуто.

З приватних коефіцієнтів можна дійти невтішного висновку про обгрунтованості включення змінних у регресійну модель. Якщо значення коефіцієнта мало або він незначний, це означає, що зв'язок між даним чинником і результативної змінної або дуже слабка, або зовсім відсутня, тому фактор можна виключити з моделі.

При порівнянні коефіцієнтів парної та приватної кореляції видно, що через вплив міжфакторної залежності між х і відбувається завищення оцінки тісноти зв'язку між змінними.

Аналіз мультиколлінеарності .

Якщо факторні змінні пов'язані строгою функціональною залежністю, то говорять про повну мультиколінеарність. У цьому випадку серед стовпців матриці факторних змінних Х є лінійно залежні стовпці, і за якістю визначників матриці, det(X T X = 0).

Вид мультиколлінеарності, при якому факторні змінні пов'язані деякою стохастичною залежністю, називається частковою. Якщо між факторними змінними є високий ступінь кореляції, то матриця (X T X) близька до виродженої, тобто det(X T X ≧ 0) (чим ближче до 0 визначник матриці міжфакторної кореляції, тим сильніша мультиколлінеарність факторів і ненадійніше результати множинної регресії).

Обчислення визначника показано у шаблоні рішення Excel

1. Аналіз мультиколлінеарності на основі матриці коефіцієнтів кореляції.

Якщо матриці є межфакторный коефіцієнт кореляції r xjxi > 0.7, то даної моделі множинної регресії існує мультиколлинеарность.

У разі всі парні коефіцієнти кореляції |r|<0.7, що свідчить про відсутність мультиколлинеарности чинників.

2. Рідж-регресія.

Найбільш детальним показником наявності проблем, пов'язаних з мультиколлінеарністю, є коефіцієнт збільшення дисперсії, що визначається для кожної змінної як:

де R j 2 коефіцієнт множинної детермінації в регресії X j на інші X.

Про мультиколлінеарність свідчить VIF від 4 і вище хоча б для одного j.

Критерієм поганої обумовленості є висока величина відношення max / min максимального і мінімального власних чисел матриці X T X - званого показником обумовленості. Це співвідношення також дозволяє судити про рівень серйозності проблем мультиколлінеарності: показник обумовленості в межах від 10 до 100 свідчить про помірну колінеарність, понад 1000 — дуже серйозну колінеарність.

Модель регресії у стандартному масштабі передбачає, що це значення досліджуваних ознак перетворюються на стандарти (стандартизовані значення).

Таким чином, початок відліку кожної стандартизованої змінної поєднується з її середнім значенням, а як одиниця зміни приймається її середнє квадратичне відхилення S .

Якщо зв'язок між змінними в природному масштабі лінійний, то зміна початку відліку та одиниці виміру цієї властивості не порушать, так що і стандартизовані змінні будуть пов'язані лінійним співвідношенням:

t y = ∑β j t xj

Для оцінки β-коефіцієнтів застосуємо МНК. При цьому система нормальних рівнянь матиме вигляд:

r x1y = β 1 + r x1x2•β 2 + ... + r x1xm • β m

r x2y = r x2x1 • β 1 + β 2 + ... + r x2xm • β m

...

r xmy = r xmx1 • β 1 + r xmx2 •β 2 + ... + β m

Для наших даних (беремо з матриці парних коефіцієнтів кореляції):

0.177 = β 1 -0.0372β 2 + 0.298β 3

0.84 = -0.0372β 1 + β 2 -0.214β 3

-0.258 = 1 -0.214β2 + β 3

Дану систему лінійних рівнянь розв'язуємо методом Гауса: β 1 = 0.222; β 2 = 0.839; β 3 = -0.0451;

Стандартизована форма рівняння регресії має вигляд:

t y = 0.222x 1 + 0.839x 2 -0.0451x 3

Знайдені з даної системи β-коефіцієнти дозволяють визначити значення коефіцієнтів у регресії у природному масштабі за формулами:

3. Аналіз параметрів рівняння регресії .

Перейдемо до статистичного аналізу отриманого рівняння регресії: перевірки значущості рівняння та його коефіцієнтів, дослідження абсолютних та відносних помилок апроксимації

Для незміщеної оцінки дисперсії виконаємо наступні обчислення:

Незміщена помилка ε = Y - Y(x) = Y - X * s (абсолютна помилка апроксимації)

Середня помилка апроксимації

Оцінка дисперсії дорівнює:

s e 2 = (YY (X)) T (YY (X)) = 318.138

Незміщена оцінка дисперсії дорівнює:

Оцінка середньоквадратичного відхилення ( стандартна помилка для оцінки Y ):

Знайдемо оцінку коварійної матриці вектора 2 • (X T X) -1

Дисперсії параметрів моделі визначаються співвідношенням S 2 i = K ii , тобто. це елементи, що лежать на головній діагоналі

Показники тісноти зв'язку факторів із результатом .

Якщо факторні ознаки різні за своєю сутністю та (або) мають різні одиниці виміру, то коефіцієнти регресії b j при різних факторах є непорівнянними. Тому рівняння регресії доповнюють сумірними показниками тісноти зв'язку фактора з результатом, що дозволяють ранжувати фактори за силою впливу на результат.

До таких показників тісноти зв'язку відносять: часткові коефіцієнти еластичності, β-коефіцієнти, часткові коефіцієнти кореляції.

Приватні коефіцієнти еластичності .

З метою розширення можливостей змістовного аналізу моделі регресії використовуються приватні коефіцієнти еластичності, які визначаються за формулою:

Приватний коефіцієнт еластичності показує, наскільки відсотків в середньому змінюється ознака-результат у зі збільшенням ознаки-фактора х j на 1% від свого середнього рівня при фіксованому положенні інших факторів моделі.

За зміни фактора х 1 на 1%, Y зміниться на 0.0437%. Частковий коефіцієнт еластичності | E 1 | < 1. Отже, його впливом геть результативний ознака Y незначно.

За зміни фактора х 2 на 1%, Y зміниться на 0.782%. Частковий коефіцієнт еластичності | E 2| < 1. Отже, його впливом геть результативний ознака Y незначно.

При зміні фактора х 3 на 1% Y зміниться на -0.00556%. Приватний коефіцієнт еластичності | E 3 | < 1. Отже, його впливом геть результативний ознака Y незначно.

Стандартизовані приватні коефіцієнти регресії .

Стандартизовані приватні коефіцієнти регресії - β-коефіцієнти (β j ) показують, яку частину свого середнього квадратичного відхилення S(у) зміниться ознака-результат y зі зміною відповідного чинника х j на величину свого середнього квадратичного відхилення (S хj) при незмінному впливі інших факторів (що входять до рівняння).

За максимальним β j можна судити, який фактор сильніше впливає на результат Y.

За коефіцієнтами еластичності та β-коефіцієнтами можуть бути зроблені протилежні висновки. Причини цього: а) варіація одного фактора дуже велика; б) різноспрямований вплив чинників результат.

Коефіцієнт j може також інтерпретуватися як показник прямого (безпосереднього) впливу j -ого фактора (x j ) на результат (y). У множинні регресії j- ий фактор надає не тільки прямий, але і непрямий (опосередкований) вплив на результат (тобто вплив через інші фактори моделі).

Непрямий вплив вимірюється величиною: ∑β i r xj,xi , де m - Число факторів в моделі. Повний вплив j-ого фактора на результат дорівнює сумі прямого та непрямого впливів вимірює коефіцієнт лінійної парної кореляції даного фактора та результату - r xj,y .

Так для нашого прикладу безпосередній вплив фактора x 1 на результат Y у рівнянні регресії вимірюється j і становить 0.222; непрямий (опосередкований) вплив даного фактора на результат визначається як:

r x1x2 β 2 = -0.0372 * 0.839 = -0.03118

Порівняльна оцінка впливу аналізованих факторів на результативну ознаку .

5. Порівняльна оцінка впливу аналізованих факторів на результативну ознаку проводиться:

- Середнім коефіцієнтом еластичності, що показує на скільки відсотків середньому за сукупністю зміниться результат y від своєї середньої величини при зміні фактора x i на 1% від свого середнього значення;

- β-коефіцієнти, які показують, що якщо величина фактора зміниться на одне середньоквадратичне відхилення S xi , то значення результативної ознаки зміниться в середньому на β свого середньоквадратичного відхилення;

- Частку кожного фактора в загальній варіації результативної ознаки визначають коефіцієнти роздільної детермінації (окремого визначення): d 2 i = r yxi β i.

d 2 1 = 0.18 * 0.222 = 0.0393

d 2 2 = 0.84 * 0.839 = 0.705

d 2 3 = -0.16 * (- 0.0451) = 0.00713

При цьому повинно виконуватися рівність:

Σd i 2 = R 2 = 0.751

Множинний коефіцієнт кореляції ( Індекс множинної кореляції).

Тісноту спільного впливу факторів на результат оцінює індекс множинної кореляції.

На відміну від парного коефіцієнта кореляції, який може набувати негативних значень, він приймає значення від 0 до 1.

Тому R не може бути використаний для інтерпретації напряму зв'язку. Чим щільніші фактичні значення yi розташовуються щодо лінії регресії, тим менша залишкова дисперсія і, отже, більша величина R y(x1,...,xm) .

Таким чином, при значенні R близькому до 1 рівняння регресії краще описує фактичні дані і фактори сильніше впливають на результат. При значенні R близькому до 0 рівняння регресії погано описує фактичні дані та фактори надають слабку дію на результат.

Коефіцієнт множинної кореляції можна визначити через матрицю парних коефіцієнтів кореляції:

де r - визначник матриці парних коефіцієнтів кореляції; Δ r11 - визначник матриці межфакторной кореляції.

Δ r =

1 0,177 0,84 -0,158

0,177 1 -0,0372 0,298

0,84 -0,0372 1 -0,214

-0,158 0,298 -0,214 1

= 0.216

Δ r11 =

1 -0,0372 0,298

-0,0372 1 -0,214

0,298 -0,214 1

= 0.869

Коефіцієнт множинної кореляції

Зв'язок між ознакою Y та факторами X i сильний

Розрахунок коефіцієнта кореляції виконаємо, використовуючи відомі значення лінійних коефіцієнтів парної кореляції та β-коефіцієнтів.

Коефіцієнт детермінації

R 2 = 0.751

Коефіцієнт детермінації .

R 2 = 0.8666 2 = 0.751

Більш об'єктивною оцінкою є скоригований коефіцієнт детермінації:

Чим ближче цей коефіцієнт до одиниці, тим більше рівняння регресії пояснює поведінку Y.

Додавання в модель нових змінних, що пояснюють, здійснюється доти, поки зростає скоригований коефіцієнт детермінації.

Висновки .

Через війну розрахунків було отримано рівняння множинної регресії: Y = 18.1829 + 0.09231X 1 + 0.9995X 2 -0.01504X 3 . Можлива економічна інтерпретація параметрів моделі: збільшення X 1 на 1 од. призводить до збільшення Y в середньому на 0.0923 од. збільшення X 2 на 1 од. призводить до збільшення Y в середньому на 0.999 од. збільшення X 3 на 1 од. призводить до зменшення Y в середньому на 0.015 од. За β 2 =0.839 робимо висновок, що найбільший вплив на результат Y має фактор X 2 .

Перевірка наявності гетероскедастичності .

Покажемо з прикладу для x 1 .

1) Методом графічного аналізу залишків .

У цьому випадку осі абсцис відкладаються значення пояснюючої змінної X, а осі ординат або відхилення e i , або їх квадрати e i 2 .

Якщо є певний зв'язок між відхиленнями, то гетероскедастичність має місце. Відсутність залежності, швидше за все, свідчить про відсутність гетероскедастичності.

2) За допомогою тесту рангової кореляції Спірмена .

Коефіцієнт рангової кореляції Спірмена .

Надамо ранги ознакою | e i | та фактору X.

Так як у матриці є пов'язані ранги (однаковий ранговий номер) 1-го ряду, зробимо їх переформування. Переформування рангів здійснюватиметься без зміни важливості рангу, тобто між ранговими номерами повинні зберегтися відповідні співвідношення (більше, менше або рівно). Також не рекомендується ставити ранг вище 1 і нижче значення, що дорівнює кількості параметрів (в даному випадку n = 20). Переформування рангів провадиться в табл.

Матриця рангів.

ранг X, d x ранг | e i |, d y (d x - d y ) 2

Перевірка правильності складання матриці на основі обчислення контрольної суми:

Сума по шпальтах матриці рівні між собою та контрольної суми, отже, матриця складена правильно.

Оскільки серед значень ознак х і зустрічається кілька однакових, тобто. утворюються пов'язані ранги, то у такому разі обчислюється коефіцієнт Спірмена

Зв'язок між ознакою | e i | та фактором X слабка та зворотна

Оцінка коефіцієнта рангової кореляції Спірмена.

Значимість коефіцієнта рангової кореляції Спірмена

Для того щоб при рівні значущості α перевірити нульову гіпотезу про рівність нулю генерального коефіцієнта рангової кореляції Спірмена при конкуруючої гіпотезі H i . p ≠ 0, треба обчислити критичну точку

де n – обсяг вибірки; p - вибірковий коефіцієнт рангової кореляції Спірмена: t(α, к) - критична точка двосторонньої критичної області, яку знаходять за таблицею критичних точок розподілу Стьюдента, за рівнем значущості α і числом ступенів свободи k = n-2.

Якщо |p| < Т kp- немає підстав відкинути нульову гіпотезу. Ранговий кореляційний зв'язок між якісними ознаками не значущий. Якщо |p| > T kp - нульову гіпотезу відкидають. Між якісними ознаками існує значний ранговий кореляційний зв'язок.

За таблицею Стьюдента знаходимо t(α/2, k) = (0.05/2;18) = 2.445

Оскільки T kp > p, то приймаємо гіпотезу про рівність 0 коефіцієнта рангової кореляції Спірмена. Іншими словами, коефіцієнт рангової кореляції статистично - не значущий і ранговий кореляційний зв'язок між оцінками по двох тестах незначний.

Перевіримо гіпотезу H 0 : гетероскедастичність відсутня.

Оскільки 2.445 > 0.56, гіпотеза про відсутність гетероскедастичності приймається.

3. Тест Голдфелда-Квандта .

У разі передбачається, що стандартне відхилення σ i = σ(ε i ) пропорційно значенню x i змінної X у цьому спостереженні, тобто. σ 2 i = σ 2 x 2 i , i = 1,2, ..., n.

Тест Голдфелда-Квандта полягає в наступному:

1. Всі n спостережень упорядковуються за величиною X.

2. Уся впорядкована вибірка після цього розбивається на три підвиборні розмірності k, (n-2k), k.

3. Оцінюються окремі регресії для першої підвиборки (k перших спостережень) та для третьої підвиборки (k останніх спостережень).

4. Для порівняння відповідних дисперсій будується відповідна F-статистика:

F = S 3 /S 1

Побудована F-статистика має розподіл Фішера з числом ступенів свободи v 1 = v 2 = (n – c - 2m)/2.

5. Якщо F > F kp , гіпотеза про відсутність гетероскедастичності відхиляється.

Цей же тест може використовуватися при припущенні про зворотну пропорційність між і і значеннями пояснюючої змінної. У цьому статистика Фішера має вигляд:

F = S 1 /S 3

1. Упорядкуємо всі значення за величиною X.

2. Знаходимо розмір підвиборки k = (20 - 5)/2 = 8.

де c = 4n/15 = 4 * 20/15 = 5

3. Оцінимо регресію для першої вибірки.

Знаходимо параметри рівняння методом найменших квадратів .

Система рівнянь МНК:

a 0 n + a 1 Σx = Σy

a 0 Σx + a 1 Σx 2 = Σy • x

Для наших даних система рівнянь має вигляд:

8a 0 + 227a 1 = 806

227a 0 + 8299a 1 = 23197

З першого рівняння виражаємо а 0 і підставимо у друге рівняння

Отримуємо a 0 = 0.18, a 1 = 95.76

x і х 2 y 2 х * у y (x) (yy (x)) 2

7 93 49 8649 651 96.991 15.926

14 102 196 10404 1428 98.222 14.275

18 90 324 8100 1620 98.925 79.661

18 112 324 12544 2016 98.925 170.947

33 99 1089 9801 3267 101.563 6.571

40 95 1600 9025 3800 102.795 60.755

46 110 2116 12100 5060 103.85 37.825

51 105 2601 11025 5355 104.729 0.0734

227 806 8299 81648 23197 806 386.034

Тут S 1 = 386.03 оцінимо

регресію для третьої підвиборки.

Знаходимо параметри рівняння методом найменших квадратів .

Система рівнянь МНК:

a 0 n + a 1 Σx = Σy

a 0 Σx + a 1 Σx 2 = Σy • x

Для наших даних система рівнянь має вигляд:

8a 0 + 513a 1 = 807

513a 0 + 33087a 1 = 51902

З першого рівняння виражаємо а 0 і підставимо на друге рівняння

Отримуємо a 0 = 0.8, a 1 = 49.43

x і х 2 y 2 х * у y (x) (yy (x)) 2

56 96 3136 9216 5376 94.357 2.7

61 108 3721 11664 6588 98.368 92.775

62 105 3844 11025 6510 99.17 33.986

63 89 3969 7921 5607 99.972 120.396

64 92 4096 8464 5888 100.775 76.996

64 97 4096 9409 6208 100.775 14.249

71 115 5041 13225 8165 106.39 74.127

72 105 5184 11025 7560 107.193 4.807

513 807 33087 81949 51902 807 420.034

Тут S 3 = 420.03

Число ступенів свободи v1 = v2 = (n – c - 2m)/2 = (20 - 5 - 2*1)/2 = 6.5

Fkp(6.5,6.5) = 5.59

Будуємо F-статистику:

F = 420.03/386.03 = 1.09

Оскільки F < F kp = 5.59, то гіпотеза про відсутність гетероскедастичності приймається .

Перевірка на наявність автокореляції залишків .

Важливою причиною побудови якісної регресійної моделі МНК є незалежність значень випадкових відхилень від значень відхилень в інших спостереженнях. Це гарантує відсутність корелювання між будь-якими відхиленнями і, зокрема, між сусідніми відхиленнями.

Автокореляція (послідовна кореляція)визначається як кореляція між показниками, що спостерігаються, упорядкованими в часі (тимчасові ряди) або в просторі (перехресні ряди). Автокореляція залишків (відхилень) зазвичай трапляється у регресійному аналізі під час використання даних часових рядів і дуже рідко під час використання перехресних даних.

В економічних завданнях значно частіше зустрічається позитивна автокореляція , ніж негативна автокореляція . Найчастіше позитивна автокореляція викликається спрямованим постійним впливом деяких неврахованих у моделі чинників.

Негативна автокореляціяФактично означає, що з позитивним відхиленням слід негативне і навпаки. Така ситуація може мати місце, якщо ту саму залежність між попитом на прохолодні напої та доходами розглядати за сезонними даними (зима-літо).

Серед основних причин, що викликають автокореляцію , можна назвати такі:

1. Помилки специфікації. Необлік моделі будь-якої важливої ​​пояснюючої змінної чи неправильний вибір форми залежності зазвичай призводять до системним відхиленням точок спостереження лінії регресії, що може зумовити автокореляцію.

2. Інерція. Багато економічних показників (інфляція, безробіття, ВНП і т.д.) мають певну циклічність, пов'язану з хвилеподібністю ділової активності. Тому зміна показників відбувається не миттєво, а має певну інертність.

3. Ефект павутиння. У багатьох виробничих та інших сферах економічні показники реагують зміну економічних умов із запізненням (тимчасовим лагом).

4. Згладжування даних. Найчастіше дані по деякому тривалому часовому періоду отримують усереднення даних по складових його інтервалах. Це може призвести до певного згладжування коливань, які були всередині періоду, що розглядається, що в свою чергу може бути причиною автокореляції.

Наслідки автокореляції схожі з наслідкамигетероскедастичності : висновки з t- і F-статистиків, що визначають значимість коефіцієнта регресії та коефіцієнта детермінації, можливо, будуть невірними.

Виявлення автокореляції

1. Графічний метод

Є низка варіантів графічного визначення автокореляції. Один з них пов'язує відхилення i з моментами їх отримання i. При цьому по осі абсцис відкладають або час отримання статистичних даних, або порядковий номер спостереження, а по осі ординат - відхилення i (або оцінки відхилень).

Природно припустити, якщо є певна зв'язок між відхиленнями, то автокореляція має місце. Відсутність залежності швидше за все свідчить про відсутність автокореляції.

Автокореляція стає наочнішою, якщо побудувати графік залежності ε i від ε i-1

2. Коефіцієнт автокореляції .

Якщо коефіцієнт автокореляції r ei < 0.5, то є підстави стверджувати, що автокореляція відсутня.

Для визначення ступеня автокореляції обчислимо коефіцієнт автокореляції та перевіримо його значущість за допомогою критерію стандартної помилки. Стандартна помилка коефіцієнта кореляції розраховується за формулою:

Коефіцієнти автокореляції випадкових даних повинні мати вибірковий розподіл, що наближається до нормального з нульовим математичним очікуванням і середнім квадратичним відхиленням, рівним

Якщо коефіцієнт автокореляції першого порядку r 1знаходиться в інтервалі:

-2.473 * 0.224 < r 1 < 2.473 * 0.224

можна вважати, що дані не показують наявність автокореляції першого порядку.

Використовуючи розрахункову таблицю, отримуємо:

Оскільки -0.553 < r 1 = 0.319 < 0.553, то властивість незалежності залишків виконується. Автокореляція відсутня.

3. Критерій Дарбіна-Уотсона .

Цей критерій є найбільш відомим виявлення автокореляції.

При статистичному аналізі рівняння регресії на початковому етапі часто перевіряють здійсненність однієї причини: умови статистичної незалежності відхилень між собою. При цьому перевіряється некорельованість сусідніх величин e i .

і y (x) e i = yy (x) e 2 (e i - e i-1 ) 2

90 89.695 0.305 0.0929

92 93.286 -1.286 1.653 2.53

89 95.493 -6.493 42.163 27.118

93 105.331 -12.331 152.046 34.075

95 93.632 1.368 1.87 187.643

90 84.057 5.943 35.317 20.933

97 100.402 -3.402 11.576 87.333

96 98.101 -2.101 4.415 1.693

99 99.901 -0.901 0.811 1.441

102 99.342 2.658 7.066 12.666

100 100.255 -0.255 0.0651 8.488

105 105.867 -0.867 0.752 0.375

106 105.108 0.892 0.795 3.094

108 106.685 1.315 1.728 0.179

105 104.733 0.267 0.0715 1.097

105 104.276 0.724 0.525 0.209

110 107.113 2.887 8.338 4.68

112 106.587 5.413 29.302 6.379

113 111.152 1.848 3.414 12.713

115 110.983 4.017 16.136 4.706

318.138 417.351

Для аналізу корелюваності відхилень використовують статистику Дарбіна-Уотсона :

Критичні значення d 1 і d 2 визначаються на основі спеціальних таблиць для необхідного рівня значущості α, числа спостережень n = 20 і кількості змінних, що пояснюють m=3.

Автокореляція відсутня, якщо виконується така умова:

d 1 < DW і d 2 < DW < 4 - d 2 .

Не звертаючись до таблиць, можна скористатися приблизним правилом і вважати, що автокореляція залишків відсутня, якщо 1.5 < DW < 2.5. Оскільки 1.5>1.31<2.5, то автокореляція залишків присутня .

Для надійнішого висновку доцільно звертатися до табличних значень.

По таблиці Дарбіна-Уотсона для n = 20 і k = 3 (рівень значимості 5%) знаходимо: d 1 = 1.00; d 2 = 1.68.

Оскільки 1.00 < 1.31 і 1.68 > 1.31 < 4 - 1.68, то автокореляція залишків є .

Мультіколінеарність

Звільнення від мультіколінеарності

Гетеродаксичність

Тест Гольдфера Кванта

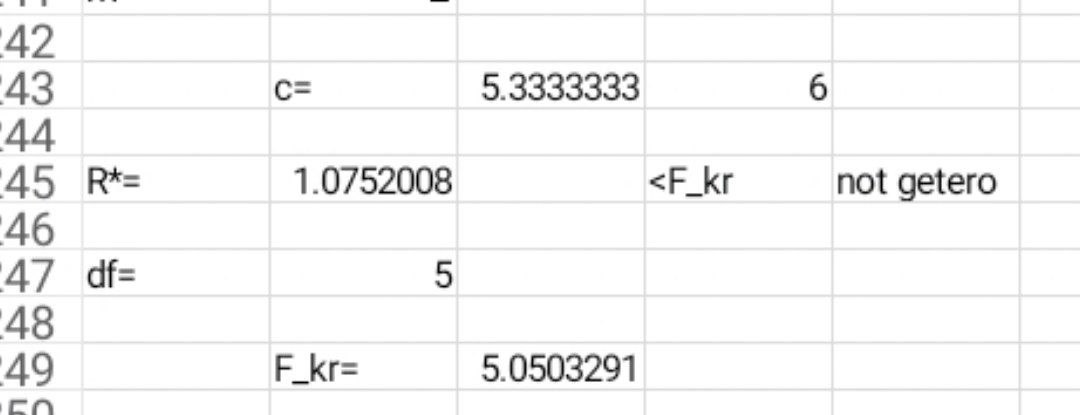
Тест Глейсера

Тест Спирмена

Тест Парка

Автокореляція