Добавил:

posterp Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Днепропетровский национальный университет железнодорожного транспорта им. академика В. Лазаряна

Предмет:

Сопротивление материалов

Файл:

Розрахунок прямокутної пластини при згині

.pdf

Скачиваний:

Добавлен:

27.04.2021

Размер:

367.36 Кб

Скачать

☆

<<< < Предыдущая 12 / 22

E z

+ν

;

+ν

(1 −ν

−ν

ρx

ρy

)

ρy

)

ρx

Підставимо в ці співвідношення залежність кривизни від функції прогинів пластинки

1	≈ −	d 2 w	;	1	≈ −	d 2 w	.
ρx		d x2		ρy		d y2

Після підстановки отримаємо

E z

σx

= −

+ν d

;

−ν

2 ) d x2

d y2

E z

σy

= −

+ν d

(9)

−ν

2 ) d y2

d x2

Ці вирази з врахуванням (4) дають змогу записати співвідношення для згинальних моментів

M x

;

M y

(10)

= −D

∂

+ν

∂

= −D

∂

+ν

∂

∂x

∂y

∂x

В загальному випадку згину пластин (при поперечному згині) відбувається також кручення елемента поперечного перерізу пластини. При цьому вертикальними дотичними напруженнями можемо нехтувати, а враховувати слід лише горизонтальні дотичні напруження. Розглядаючи викривлення серединної поверхні пластинки викликаної крученням можна аналогічним чином вивести формулу залежності крутного момента від функції прогинів:

M xy = H = −D(1−ν)	∂2w	.	(11)
	∂x∂y

Розглянемо нескінченно малий елемент пластини розміром d x ×d y . На

гранях цього елемента виникають три погонних (віднесених до одиниці ширини перерізу) внутрішніх зусилля: згинальні і крутний моменти та поперечні сили. Нехай цей елемент пластини перебуває під дією розподіленого навантаження q(x, y). Тоді умови рівноваги елемента (після відкидання величин

вищих порядків малості) будуть мати вигляд:

∑Fz = 0 :	d Q		+		d Qy		= −q ;
		x
	d x				d y

∑M x = 0 :		d M	x	+		d M xy		=Qy ;	(12)
		d y				d x

∑M y = 0 :	d M y	+	d M xy	=Qx .

	d x d y

Враховуючи вирази для згинальних та крутного моментів (10) - (11) отримаємо з другого і третього рівнянь (12):

Qx = −D

∂

∂2w

Qy = −D

∂

∂2w

∂x2

;

∂x2

∂x2 .

(13)

∂x

∂y

Підставляючи ці формули в перше рівняння (12), отримуємо диференціальне рівняння серединної поверхні пластини (рівняння Софі Жермен):

∂4w	+ 2	∂4w	+	∂4w	=	q(x, y)	,	(14)
∂x4		∂x2∂y2		∂y4		D

де q(x, y) - інтенсивність поперечного поверхневого навантаження.

maxτxy

	H	M x				x
	H	x				x
		x	τyx

					σx
			τ	xy	σx	maxσx
	Qx		τ			maxσx
					τ
					τ
M y					zx
M y	Qy	y σy	τzy
	Qy	y σy	τzy

Рис. 4. Рис. 5.

Таким чином, задача згину пластинки зводиться до інтегрування рівняння (14). Якщо функція прогинів знайдена, то зусилля і напруження, які виникають в пластинці, знаходяться за формулами:

а) в перерізі з нормаллю, яка паралельна осі x :

w2 +

M x = −D

∂

ν ∂

; M xy = H = −D(1−ν)

∂

;

∂x

∂y

∂x∂y

б) в перерізі з нормаллю, яка паралельна осі y :

∂

M y = −D

+ν

; M xy = H = −D(1−ν)

∂

;

∂x∂y

∂y

∂x

= −D	∂	(∆w) .	(15)
	∂x

Qy = −D ∂∂y (∆w) . (16)

На рис. 3 показані додатні напрямки внутрішніх зусиль. Кожний з шести силових факторів взаємозв’язаний з відповідним напруженням, додатній напрямок якого показано на рис. 4.

Напруження σx , σy , τxy виражаються через відповідні внутрішні зусилля таким чином (рис. 5):

σx =	12M	x	z ;	σy =	12M y	z ;	τxy =	12H	z .	(17)
	h3				h3			h3

Із виразів (17) видно, що нормальні напруження σx , σy										і горизонтальне
дотичне напруження τxy				(τyx ) змінюються по висоті перерізу за лінійним за-

коном. Вони набувають найбільших значень в точках, які прилягають до поверхні пластинки (z = ±h 2) , а на серединній поверхні дорівнюють нулеві,

тобто:

6M y

maxσ

;

maxσ

; maxτ

(18)

Епюри напружень σx

іτyx

показані на рис. 5. Ці напруження є визнача-

льними при оцінці міцності пластинки. Вертикальні дотичні напруження τzx і τzy , що зв’язані з погонними поперечними силами Qx і Qy , при розрахунках

пластинки на міцність, як правило, не враховуються.

При розв’язуванні рівняння Софі Жермен виникають сталі інтегрування, які залежать від способу закріплення контуру пластинки і діючих на ньому навантажень. Ці сталі визначаються з умов на контурі пластинки (на кожному краї пластинки формулюються дві граничні умови).

Умови на контурі пластинки (граничні умови). Розрізняють три осно-

вні типи закріплення країв пластинки: жорстко закріплений, шарнірно опертий та вільний (не закріплений).

1.Якщо край пластинки є жорстко закріплений, то на цьому краї прогин і кут повороту в напрямку, що є перпендикулярний до краю, дорівнює нулю.

2.Якщо край пластинки шарнірно опертий і не навантажений момен-

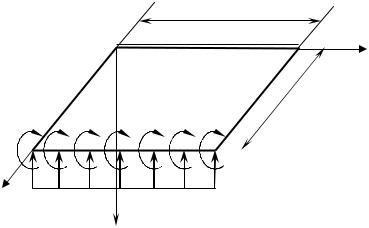
тами, то на цьому краю прогин і згинальний момент дорівнюють нулеві. Якщо край навантажений торцевим розподіленим моментом, то згинальний момент дорівнює торцевому моменту.

3.Якщо край пластинки вільний (не закріплений і вільний від навантаження), то на цьому краю згинальний момент і поперечна сила дорівнюють нулеві.

4.Якщо край пластинки вільний від закріплення, але навантажений розподіленим торцевим моментом і вертикальним навантаженням, то на цьому краї згинальний момент дорівнює торцевому моменту, а зведена поперечна сила – вертикальному значенню сили.

		a		Згинальний	момент
B			C	вважається додатнім, якщо
				він згинає пластинку опук-
			x
				лістю вниз. Знак поперечної
			b	сили співпадає зі знаком від-
				повідного їй дотичного на-
	M0
A				пруження. Тому, якщо на то-

		D		рцевій грані пластинки, зов-
y
	q0 Рис. 6 .			нішня нормаль якої співпадає
z				з додатнім напрямком пара-

лельної їй координатної осі, вертикальне навантаження напрямлено вниз, то воно викликає додатну поперечну силу (в граничну умову підставляється зі знаком „+”).

Приклади запису граничних умов. Для пластини (рис. 6), сторона АВ якої жорстко закріплена, сторона ВС - шарнірно оперта, сторона CD - вільна і сторона DA вільна від закріплення, але навантажена розподіленими торцевими моментами M0 і силами q0 , потрібно записати в загальному вигляді грани-

чні умови.

∂w

Край АВ (жорстко закріплений) :

x = 0;

0 ≤ y ≤b;

w = 0;

= 0 .

∂x

Край ВС (шарнірно опертий):

y =0;

0 ≤ x ≤ a;

w = 0;

M y

= 0 .

Край СD (вільний): x = a;

0 ≤ y ≤b;

w = 0; M x = 0 або

∂2w

+ν

∂2w

= 0

;

∂x2

∂y2

зв

= 0 або

∂3w

+(2

−ν)

∂2w

=0 .

∂w3

∂x∂y2

Край АD (вільний від закріплення, але навантажений рівномірно розподіленим торцевим моментом M0 і вертикальним навантаженням q0 ):

y =b; 0 ≤ x ≤ a; M

= M

;

Qзв = −q ,

або −D

∂2w

+ν

∂2w

= M

0 ; −D

∂3w

+(2 −ν)

∂3w

= −q0 .

∂y2

∂x2

∂y3

∂x2∂y

В останній умові вертикальне розподілене навантаження q0 підставлене

JJG

зі знаком „-” , так як на краю АD зовнішня нормаль nAD співпадає з додатнім напрямком осі y , а навантаження напрямлене вверх.

Приклад розв’язування задачі.

0	A	Дано прямокутну пластинку,
		x віднесену до декартової системи ко-

ординат x0 y (рис. 7), яка знаходиться

C	B
y	a

Рис. 7.

bпід дією поперечного рівномірно розподіленого навантаження інтенсивності q0 . Функцію прогинів пластинки

w(x, y) задано з точністю до постійного множника K :

w(x, y) = Kx(x −a)( y −b)2 .

Потрібно визначити цей постійний множник і характер закріплення пластин-

ки, побудувати епюри внутрішніх зусиль в перерізі			x = a	2	і	y = b	2	і знайти
	σx ,σy ,τxy . При			2			2
найбільше значення напружень	σx ,σy ,τxy . При		розрахунках				прийняти:
a = 2 м; b =1м; h =0.1м; ν = 0.25 ; q		= 40 кН/м2.
0

Розв'язування:

1.Використовуючи диференціальне рівняння зігнутої серединної поверхні пластинки, визначимо постійний коефіцієнт K . Для цього знайдемо ча-

стинні похідні функції прогину:

∂w

= K (2x −a)( y −b)2 ,

∂w

= 2Kx(x −a)( y −b) ;

(а)

∂x

∂y

w2 = 2Kx(x −a) ,

∂

= 2K ( y −b)2 ,

∂

∂ w

∂

= 4K ( y −b) ; (б)

∂x

∂y

∂x ∂y

∂y

∂x

∂4w

= 0 ,

∂4w

= 0 ,

∂4w

∂

∂3w

= 4K .

(в)

∂x

∂y

∂x

∂y

Підставимо знайдені значення похідних в рівняння Софі Жермен, тоді одержимо K = 8qD0 .

2. Встановлюємо, яким граничним умовам задовольняє задана функ-

ція прогинів. Для цього розглянемо геометричні граничні умови (прогини і кути повороту на контурі пластинки).

Як видно з виразу (а) при x = 0 , w = 0 ; при x = a , w = 0 ; при y = 0 , w ≠ 0 ; при y =b w = 0 . Так як на краях АВ, СВ і ОС прогини дорівнюють нулеві, то

ці краї можуть бути або шарнірно оперті, або жорстко закріплені. Край ОА вільний від закріплення (на цьому краї прогин не дорівнює нулеві).

Як випливає з виразів (б) при	x =0,	∂w	≠ 0 ; при	x = a,	∂w	≠ 0 ;
		∂x			∂x

при y =b, ∂∂wy =0 . Отже, край СВ ( y =b ) жорстко закріплений. На краях ОС

( x = 0 ) і АВ ( x = a ) кути повороту не дорівнюють нулеві. Тому ці краї є шарнірно оперті. Однак, вони можуть бути навантажені розподіленим згинальним моментом. Перевіримо наявність цих моментів:

Край ОС

M x		2	w2		2	w2		= −2KD( y −b)2 = −	1 q0 ( y −b)2	≠ 0 ;
M x	= −D	∂	w2	+ν	∂	w2		= −2KD( y −b)2 = −	1 q0 ( y −b)2	≠ 0 ;
		∂x			∂y		x=0		4
Край АВ
M x		2	w2		2	w2		= −2KD( y −b)2 = −	1 q0 ( y −b)2	≠ 0 .
M x	= −D	∂	w2	+ν	∂	w2		= −2KD( y −b)2 = −	1 q0 ( y −b)2	≠ 0 .
		∂x			∂y		x=a		4

Отже, до шарнірно опертих країв ОС і АВ прикладене розподілене моментне навантаження, яке змінюються за параболічним законом.

Перевіримо наявність навантаження на вільному краї ОА ( y = 0 ):

M y

= −2KD[x(x −a)

−νb2 ] = −

1 q0[x(x −a) −νb2

] ;

= −D

∂

+ν

∂

∂y

∂x

y=0

Qyзв = −D

∂

+(2 −ν)

∂ w

= −4KD(2

−ν)b = −1 q0 (2 −ν)b .

∂y

∂x

∂y y=0

Звідси випливає, що край ОА навантажений згинальним моментом, який змінюється за параболічним законом і рівномірно розподіленим вертикальним навантаженням, яке напрямлене вверх.

3. Складемо вирази для згинальних і крутних моментів та поперечних сил. Згинальні моменти:

M		= −D	∂2w	+ν	∂2w	= −	1 q [( y −b)2	+νx(x −a)];
	x		∂x2		∂y2		4 0

= −D

∂2w +ν ∂2w = −1 q

[x(x −a) +ν( y −b)2

] .

∂y2

∂x2

Крутний момент:

∂3w

H = −D

∂x3

= −

4 (1

−ν)q0 (2x −a)( y −b) .

∂x∂y2

Поперечні сили:

∂3w

Qx = −D

∂y3

= −

4 q0

(2x −a) ;

∂x∂y2

∂3w

Qy = −D

∂y3

= −

2 q0

( y −b) .

∂y∂x2

4. Побудуємо епюри внутрішніх силових факторів для двох перерізів x =1м і y =0.5м; формули для визначення внутрішніх зусиль з врахуван-

ням числових значень q0 , a, b і ν набувають вигляду:

а) для перерізу І-І

( x =1, 0 ≤ y ≤1)

= −

1 q

[( y −b)2 +νx(x −a)]

x=1

= −10[( y −1)2

−0.25]

(kH м/ м) ,

= −

1 q

[x(x −a) +ν( y −b)2 ]

x=1

= −10[−1+

0.25( y −1)2 ] (kH м/ м) ,

H = −

1 q (1−ν)(2x −a)( y −b)

= 0 (kH м/ м) ,

x=1

Q = −

1 q

(2x −a)

= 0 (kH / м) ,

x=1

= −1 q

( y −b)

= −20( y −1) (kH / м) ,

x=1

б) для перерізу ІІ-ІІ ( y =0.5,

0 ≤ x ≤ 2)

= −1 q

[( y −b)2 +νx(x −a)]

= −2.5[1

+ x(x −2)]

(kH м/ м) ,

y=0.5

= −1 q

[x(x −a) +ν( y −b)2 ]

= −10[x(x −2) +0.0625] (kH м/ м) ,

y=0.5

H = −

1 q (1−ν)(2x −a)( y −b)

= 7.5(x −1)

(kH м/ м) ,

y=0.5

Q = −

1 q

(2x −a)

= −20(x −1) (kH / м) ,

= −1 q

( y −b)

=10 (kH / м) .

y=0,5

Обчислені за цими виразами значення зусиль в характерних точках перерізів наведені в табл.3, і 4.

	Точки y,(м)				Таблиця 3
Зусилля	Точки y,(м)

	0	0.25	0.5	0.75	1.0
M x ,kH м/ м	-7.5	-3.125	0	1.825	2.5
M y , kH м/ м	7.5	8.59	9.37	9.84	10

Н,kH м/ м	0	0	0	0	0
Qx , kH / м	0	0	0	0	0
Qy ,kH / м	20	15	10	5	0
	Точки x,(м)				Таблиця 4
Зусилля	Точки x,(м)

	0	0.5	1.0	1.5	2.0
M x ,kH м/ м	-2.5	-0.625	0	-0.625	-2.5
Mн,kH м/ м	-0.625	6.875	9.375	6.875	-0.625
Н,kH м/ м	-7.5	-3.75	0	3.75	7.5
Qx , kH / м	20	10	0	-10	-20
Qx , kH / м	10	10	10	10	10

На основі одержаних числових результатів будуємо епюри внутрішніх зусиль

M x , M y , H , Qx , Qy (рис. 8).

5. За побудованими епюрами визначаємо найбільші значення нормальних σx , σy і дотичного τxy напружень (див. рис.2):

max M x = M x	x=1	= 7.5 (kH м/ м) ;

	y=0

max M y = M y				x=1 =10								(kH м/ м) ;
max H = H				y=1							(kH м/ м) .
			x=0			= 7.5
			x=0			= 7.5
			y=0.5
За формулами знаходимо:
maxσx =	6	max M x						=					6 7.5			= 0.45 МПа;
	6	max M x											6 7.5

			h		2							2		10	4
			h								0.1			10
maxσy =	6	max M y							=				6 10			= 0.6 МПа;
	6	max M y											6 10

			h		2								2	10	4
			h								0.1			10
maxτxy =	6	max				H	=						6 7.5		= 0.45МПа.
	6	max				H

	2												2 4
			h							0.1 10

7,5

x =1м	I

							3,12		y = 0.5м	x
									y = 0.5м
			20			7,5		II		II
			15				0	II		II
			15		8,59		0
0	5	10			9,37		1,82
	5				9,37

Qy	Q		H		9,84	M	2,5	y	I
							x	y

		x		M y
				M y	10
					10	2,5			2,5
						2,5	0, 62		2,5
			20				0, 62	0	0, 62
			20					0	M x
									M x
					0, 62				0, 62
									M y
					6, 75			6, 75
				7,5				6, 75
				7,5	3, 75	9,37
					3, 75	9,37
						0			H
									H

3, 75

7,5

10 20

		Qy
10	10	Рис. 8 .
	10	Рис. 8 .

РЕКОМЕНДОВАНА ЛІТЕРАТУРА

1.Корнілов О. А. Опір матеріалів. – К.: ЛОГОС, 2000.

2.Писаренко Г. С., Квітка О. Л., Уманський Е. С. Опір матеріалів. – К.:

Вища школа, 1993.

3.Посацький С. Л. Опір матеріалів. – Львів, 1973.

НАВЧАЛЬНЕ ВИДАННЯ

ДОКУМЕНТОЗНАВСТВО

МЕТОДИЧНІ ВКАЗІВКИ

до виконання розрахунково-графічних робіт для студентів базових напрямів "Будівництво"

Укладачі: Харченко Є. В., д-р техн. наук, проф.; Білобран Б. С., д-р техн. наук, проф.; Стасюк Б. М., канд. фіз.-мат. наук, доц.; Мартинович Б. Т., канд. фіз.-мат. наук, доц.; Ліщинська Х. І., ас.

Редактор:

Комп'ютерне верстання:

<<< < Предыдущая 12 / 22

Соседние файлы в предмете Сопротивление материалов

#
27.04.2021404.62 Кб3Расчет_статически_неопределимых_систем_методом_сил_Метод_указания_Хлебородов_2001.pdf
#
27.04.2021764.85 Кб5Розрахунок балок при прямому згині.pdf
#
27.04.2021881.99 Кб1Розрахунок валу на витривалість.pdf
#
27.04.2021467.11 Кб2Розрахунок геометричних характеристик.pdf
#
27.04.2021504.53 Кб10Розрахунок просторової рами.pdf
#
27.04.2021367.36 Кб8Розрахунок прямокутної пластини при згині.pdf
#
27.04.2021307.12 Кб8Розрахунок стиснутих стрижнів на стійкість.pdf
#
27.04.2021420.21 Кб1Розрахунок стрижнів при крученнi.pdf
#
27.04.2021314.72 Кб7Частина1.pdf
#
27.04.2021302.3 Кб2Частина2.pdf
#
27.04.2021367.64 Кб3Частина3.pdf