Частина 2

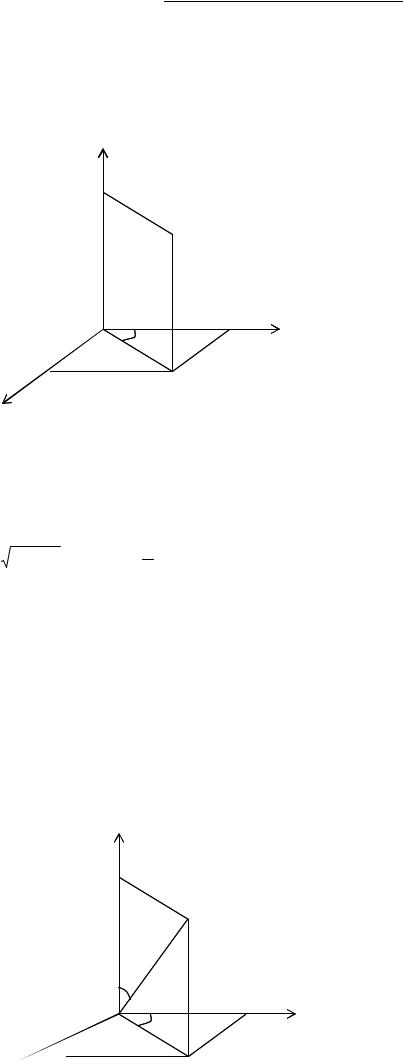
“Курс вищої математики. Частина 2.”

Найчастіше до заміни змінною в потрійному інтегралі вдаються з метою перейти від декартової прямокутної системи координат до циліндрової або сферичної системи. Див. Цилиндрическая и сферическая системы координат.

Розглянемо ці перетворення докладніше.

Циліндрова система координат.

P

z

0

θx

ρ

у

Зв'язок координат довільної точки Р простору в циліндровій системі з координатами в декартовій прямокутній системі здійснюється по формулах:

x = ρcos θy = ρsin θ

z = z

Разом:

Сферична система координат.

z

P

ρ

101

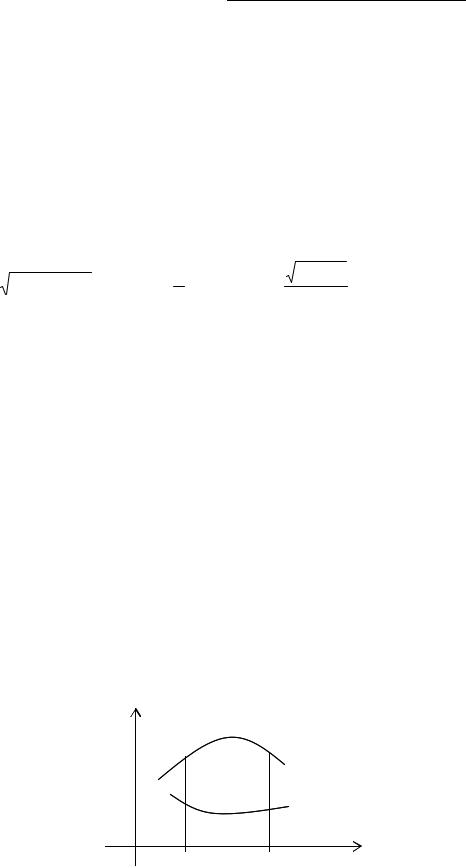
“Курс вищої математики. Частина 2.”

ϕ

у

Зв'язок координат довільної точки Р простору в сферичній системі з координатами в декартовій прямокутній системі здійснюється по формулах:

x = ρsin ϕcos θy = ρsin ϕsin θ

z = ρcos ϕ

+ ρ2 sin ϕcos ϕsin 2 θ) +ρsin ϕ(ρsin 2 ϕcos2 θ+ρsin 2 ϕsin 2 θ) = ρ2 cos2 ϕsin ϕ+ ρ2 sin3 ϕ =

= ρ2 sin ϕ.

Остаточно отримуємо:

∫∫∫F(x, y, z)dxdydz = ∫∫∫ f (ρ, ϕ,θ)ρ2 sin ϕdρdϕdθ

r τ

Геометричні і фізичні додатки кратних інтегралів.

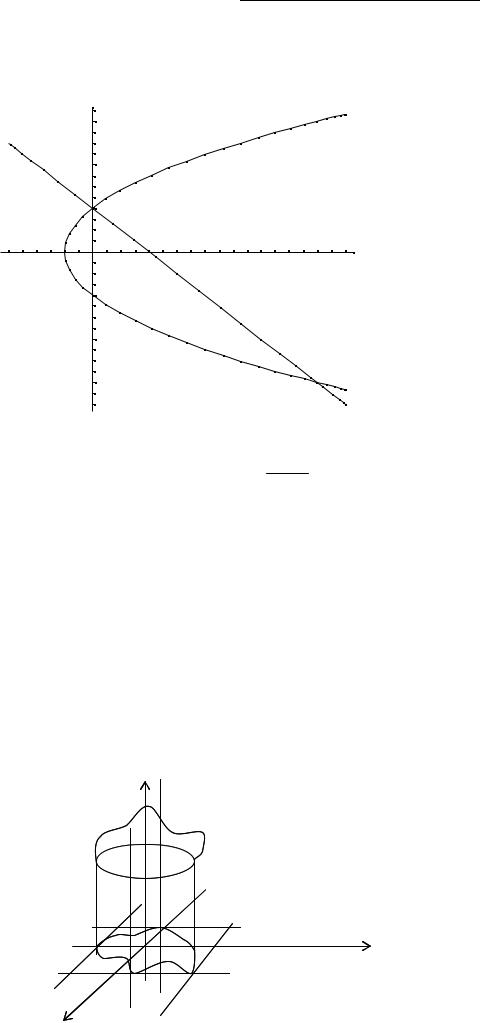
1) Обчислення площ в декартових координатах.

у

у= (x)ϕ

S

у = f(x)

Площа S, показана на малюнку може бути обчислена за допомогою подвійного інтеграла по формулі:

b ϕ( x)

S = ∫ ∫dydx

a f ( x)

102

“Курс вищої математики. Частина 2.”

Приклад. Обчислити площу фігури, обмеженої лініями y2 = 4x + 4; x + у – 2 = 0.

Побудуємо графіки заданих функцій:

Лінії перетинаються в двох крапках – (0, 2) і (8 -6). Таким чином, область інтеграції обмежена по осі Ох графіками кривих від x = y 2 4− 4 до х = 2 – у, а по осі Оу

– від –6 до 2. Тоді шукана площа рівна:

2) Обчислення площ в полярних координатах.

θ2 ϕ(θ)

S = ∫∫ρdρdθ = ∫∫dydx = ∫ ∫ρdρdθ

3) Обчислення об'ємів тіл.

Хай тіло обмежене знизу плосткостью ху, а сверху– поверхнею z = f(x,y) а з бокам – циліндровою поверхнею.

Таке тіло називається циліндроїд.

z

z = f(x, у)

x

103

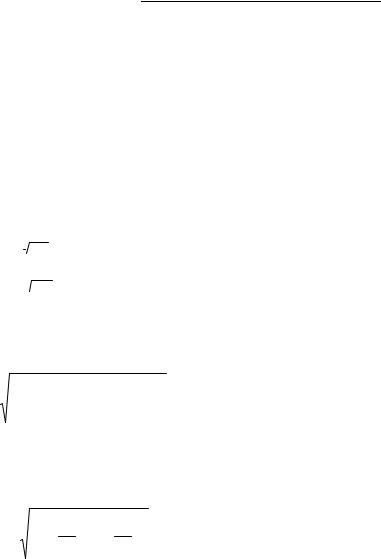
“Курс вищої математики. Частина 2.”

y2

у

V =

Приклад. Обчислити об'єм, обмежений поверхнями: x2 + y2 = 1; x + у + z =3 і площиною Хоy.

Межі інтеграції: по осі ОХ:

по осі Оy: x1 = -1; x2 = 1;

1 1−x

V = ∫ ∫(3 − x − y)dydx = 3π;

−1− 1−x2

4) Обчислення площі кривої поверхні.

Якщо поверхня задана рівнянням: f(x, у, z)= 0, то площа її поверхні знаходиться по формулі:

5)Вычисление моментів інерції площ плоских фігур.

Хай площа плоскої фігури (область ∆) обмежена лінією, рівняння якої f(x,y)= 0. Тоді моменти інерції цієї фігури знаходяться по формулах:

-щодо осі Ох:

-щодо осі Оу:

- відносно початки координат: I0 = I x + I y = ∫∫(x2 + y 2 )dydx - цей момент інерції

∆

називають ще полярним моментом інерції.

тут w – поверхнева щільність (dm = wdydx – масса елементу площі). 7) Обчислення об'ємів тіл за допомогою потрійного інтеграла.

104

“Курс вищої математики. Частина 2.”

Якщо поверхня тіла описується рівнянням f(x, у, z)= 0, то об'єм тіла може бути знайдений по формулі:

x2 y2 z2

V = ∫∫∫dzdydx

x1 y1 z1

при цьому z1 і z2 – функції від х і у або постійні, у1 і у2 – функції від х або постійні, х1

іх2 – постійні.

8)Координати центру тяжіння тіла.

У приведених вище формулах п.п. 8 – 11 r – область обчислення інтеграла за об'ємом, w – щільність тіла в крапці (х, у, z), dv – елемент об'єму

-у декартових координатах: dv = dxdydz;

-у циллиндрических координатах: dv = ρdzddθ;

-у сферичних координатах: dv = ρ2sindddθ. 12) Обчислення маси неоднорідного тіла.

M = ∫∫∫wdv;

r

Тепер щільність w – величина змінна.

105

“Курс вищої математики. Частина 2.”

Зміст:

Диференціальне числення функцій однією змінною._ Похідна функції, її геометричний і фізичний сенс. Рівняння дотичної і нормалі до кривій. Односторонні похідні функції в крапці.

Основні правила диференціювання. Похідні основних функцій. Похідна складної функції. Логарифмічне диференціювання.

Похідна показово – статечній функції. Похідна зворотної функції. Диференціал функції. Геометричний сенс диференціала. Властивості диференціала.

Диференціал складної функції. Інваріантна форма запису. Формула Тейлора.

Формула Лагранжа. Формула Маклорена.

Представлення функцій по формулі Тейлора. Біном Ньютона.

Застосування диференціала до наближених обчислень. Теореми про середній.

Теорема Ролля. Теорема Лагранжа. Теорема Коші.

Розкриття неопределенностей. Правило Лопіталя. Похідна і диференціали вищих порядків. Правила знаходження похідних.

Дослідження функцій. Зростання і убування функцій. Точки екстремуму.

Критичні крапки.

Достатні умови екстремуму.

Дослідження функцій за допомогою похідних вищих порядків. Опуклість і угнутість кривої.

Точки перегину. Асимптоти.

Схема дослідження функцій.

Векторна функція скалярного аргументу. Рівняння дотичної до кривій.

Властивості похідної векторної функції скалярного аргументу. Рівняння нормальної площини.

Параметричне завдання функції. Коло.

Еліпс. Циклоїда. Астроїда.

Похідна функції, заданої параметрично. Кривизна плоскої кривої.

106

“Курс вищої математики. Частина 2.”

Кут суміжності. Середня кривизна. Кривизна дуги в крапці. Радіус кривизни. Центр і круг кривизни. Еволюта і евольвента. Властивості еволюти.

Кривизна просторової кривої. Годограф.

Головна нормаль. Вектор і радіус кривизни. Формули Френе. Дотична площина. Бінормаль.

Кручення кривої. Інтегральне числення. Первісна функція. Невизначений інтеграл.

Властивості невизначеного інтеграла. Таблиця основних інтегралів. Безпосередня інтеграція.

Спосіб підстановки. Інтеграція по частинах. Інтеграція елементарних дробів. Рекурентна формула.

Інтеграція раціональних функцій. Інтеграція раціональних дробів. Метод невизначених коефіцієнтів. Метод довільних значень.

Інтеграція тригонометричних функцій. Універсальна тригонометрична підстановка. Інтеграція ірраціональних функцій. Біномінальні диференціали. Тригонометрична підстановка. Підстановки Ейлера.

Метод невизначених коефіцієнтів.

Інтеграли, що не виражаються через елементарні функції. Еліптичні інтеграли.

Інтеграл Пуассона. Інтеграл Френеля. Інтегральний логарифм.

Інтегральний синус і косинус. Певний інтеграл. Інтегральна сума. Інтегрована функція.

Властивості певного інтеграла. Теорема про середній. Узагальнена теорема про середній. Обчислення певного інтеграла. Теорема Ньютона – Лейбніца. Заміна змінних в певному інтегралі. Інтеграція по частинах.

107

“Курс вищої математики. Частина 2.”

Наближене обчислення певного інтеграла. Формула прямокутників.

Формула трапецій. Формула парабол (Сімпсона). Невласні інтеграли.

Абсолютна збіжність інтеграла. Інтеграл від розривної функції. Знаходження площ плоских фігур.

Знаходження площі криволінійного сектора._ Обчислення довжини дуги кривої.

Обчислення об'ємів тіл по поперечних перетинах. Обчислення об'ємів тіл обертання.

Площа поверхні тіла обертання. Функції декілька змінних. Межа.

Безперервність.

Найбільше і найменше значення. Приватний приріст.

Приватна похідна.

Геометричний сенс приватних похідних. Повний приріст і повний диференціал. Дотична площина і нормаль до поверхні.

Наближені обчислення за допомогою повного диференціала. Приватні похідні і диференціали вищих порядків. Екстремум функції декілька змінних.

Необхідні умови екстремуму. Достатні умови екстремуму. Умовний екстремум.

Функція Лагранжа. Похідна по напряму. Направляючі косинуси. Градієнт.

Зв'язок градієнта з похідній по напряму. Кратні інтеграли.

Подвійні інтеграли.

Умови існування подвійного інтеграла. Властивості подвійного інтеграла. Обчислення подвійного інтеграла. Заміна змінних в подвійному інтегралі. Якобіан.

Подвійний інтеграл в полярних координатах. Потрійний інтеграл.

Заміна змінних в потрійному інтегралі. Циліндрова система координат. Сферична система координат.

Геометричні і фізичні додатки кратних інтегралів.

108